11.3: Eliminación por sustitución
- Page ID
- 112223
Cuando la sustitución funciona mejor
Sabemos resolver una ecuación lineal en una variable. Ahora estudiaremos un método para resolver un sistema de dos ecuaciones lineales en dos variables transformando las dos ecuaciones en dos variables en una ecuación en una variable.
Para hacer esta transformación, necesitamos eliminar una ecuación y una variable. Podemos hacer esta eliminación por sustitución.
Cuando la sustitución funciona mejor
El método de sustitución funciona mejor cuando existe alguna de estas condiciones:
- Una de las variables tiene un coeficiente de 1, o
- Se puede hacer que una de las variables tenga un coeficiente de 1 sin introducir fracciones.
El método de sustitución
El método de sustitución
Para resolver un sistema de dos ecuaciones lineales en dos variables,
- Resolver una de las ecuaciones para una de las variables.
- Sustituir la expresión por la variable elegida en el paso 1 en la otra ecuación.
- Resolver la ecuación resultante en una variable.
- Sustituir el valor obtenido en el paso 3 en la ecuación obtenida en el paso 1 y resolver para obtener el valor de la otra variable.
- Verifique la solución en ambas ecuaciones.
- Escribe la solución como un par ordenado.
Conjunto de Muestras A
Resolver el sistema
\ (\ left\ {\ begin {array} {r}
2x + 3y = 14\\
3x + y = 7
\ end {array}\ right.\)
Paso 1: Dado que el coeficiente de\(y\) en la ecuación 2 es\(1\), resolveremos la ecuación 2 para\(y\).
\(y = -3x + 7\)
Paso 2: Sustituir la expresión\(-3x + 7\) por\(y\) en la ecuación 1.
\(2x + 3(-3x + 7) = 14\)
Paso 3: Resolver la ecuación obtenida en el paso 2.
\ (\ begin {alineado}
2x + 3 (-3x + 7) &= 14\\
2x - 9x + 21 &= 14\\
-7x + 21 &= 14\\
-7x &= -7\\
x &= 1
\ end {alineado}\)
Paso 4: Sustituir\(x = 1\) a la ecuación obtenida en el paso 1,\(y = -3x + 7\).
\ (\ begin {alineado}
y &= -3 (1) + 7\\
y &= -3 + 7\\
y &= 4
\ end {alineado}\)
Paso 5: Sustituir\(x = 1, y = 4\) en cada una de las ecuaciones originales para una comprobación.
1)
\ (\ begin {aligned}
2 x+3 y &=14\\
2 (1) +3 (4) &=14\ text {¿Es correcto esto? }\\
2+12 &=14\ text {¿Es correcto esto? }\\
14 &=14\ text {Sí, esto es correcto.}
\ end {alineado}\)
2)
\ (\ begin {aligned}
3x + y &= 7\\
3 (1) + (4) &= 7\ text {¿Es esto correcto? }\\
3 + 4 &= 7\ text {¿Es correcto esto? }\\
7 &= 7\ text {Sí, esto es correcto.}
\ end {alineado}\)
Paso 6: La solución es\((1, 4)\). El punto\((1, 4)\) es el punto de intersección de las dos líneas del sistema.
Conjunto de práctica A
Resolver el sistema
\ (\ left\ {\ begin {array} {r}
5x - 8y = 18\\
4x + y = 7
\ end {array}\ right.\)
- Contestar
-
El punto\((2, -1)\) es el punto de intersección de las dos líneas.
Sustitución Y Líneas Paralelas
La siguiente regla nos avisa de que las dos líneas de un sistema son paralelas.
Si los cálculos eliminan todas las variables y producen una contradicción, las dos líneas de un sistema son paralelas, y el sistema se llama inconsistente.
Conjunto de Muestras B
Resolver el sistema
\ (\ left\ {\ begin {array} {r}
2x - y = 1\\
4x - 2y = 4
\ end {array}\ right.\)
Paso 1: Resolver ecuación para\(y\).
\ (\ begin {alineado}
2x - y &= 1\\
-y &= -2x + 1\\
y &= 2x - 1
\ end {alineado}\)
Paso 2: Sustituir la expresión\(2x - 1\) por\(y\) en la ecuación 2.
\(4x - 2(2x - 1) = 4\)
Paso 3: Resolver la ecuación obtenida en el paso 2.
\ (\ begin {alineado}
4x - 2 (2x - 1) &= 4\\
4x - 4x + 2 &= 4\\
2 &\ no= 4
\ end {alineado}\)
Los cálculos han eliminado todas las variables y producen una contradicción. Estas líneas son paralelas.
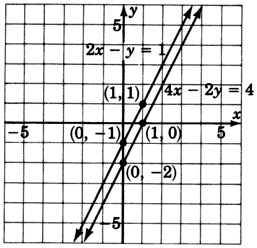
Este sistema es inconsistente.
Set de práctica B
Resolver el sistema
\ (\ left\ {\ begin {array} {r}
7x - 3y = 2\\
14x - 6y = 1
\ end {array}\ right.\)
- Contestar
-
La sustitución produce\(4 \not= 1\), o\(\dfrac{1}{2} \not = 2\), una contradicción. Estas líneas son paralelas y el sistema es inconsistente.
Sustitución y líneas coincidentes
La siguiente regla nos alerta de que las dos líneas de un sistema son coincidentes.
Si los cálculos eliminan todas las variables y producen una identidad, las dos líneas de un sistema son coincidentes y el sistema se llama dependiente.
Conjunto de Muestras C
Resolver el sistema
\ (\ left\ {\ begin {array} {r}
4x + 8y = 8\\
3x + 6y = 6
\ end {array}\ right.\)
Paso 1: Divide la ecuación 1 por\(4\) y resuelve para\(x\).
\ (\ comenzar {alineado}
4x + 8y &= 8\\
x + 2y &= 2\\
x &= -2y + 2
\ final {alineado}\)
Paso 2: Sustituir la expresión\(-2y + 2\) por\(x\) en la ecuación 2.
\(3(-2y + 2) + 6y = 6\)
Paso 3: Resolver la ecuación obtenida en el paso 2.
\ (\ comenzar {alineado}
3 (-2y + 2) + 6y &= 6\\
-6y + 6 + 6y &= 6\\
6 &= 6
\ end {alineado}\)
Los cálculos han eliminado todas las variables y han producido una identidad. Estas líneas son coincidentes.
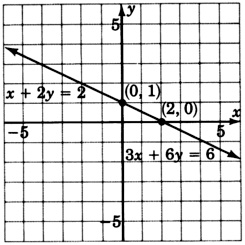
Este sistema es dependiente.
Set de práctica C
Resolver el sistema
\ (\ left\ {\ begin {array} {r}
4x + 3y = 1\\
-8x - 6y = -2
\ end {array}\ right.\)
- Contestar
-
Los cómputos producen\(-2 = -2\), una identidad. Estas líneas son coincidentes y el sistema es dependiente.
Los sistemas en los que un coeficiente de una de las variables no es\(1\) o no se puede hacer que sea\(1\) sin introducir fracciones no son muy adecuados para el método de sustitución. El problema en el Conjunto de Muestras D ilustra esta situación “desordenada”.
Conjunto de Muestras D
Resolver el sistema
\ (\ left\ {\ begin {array} {r}
3x + 2y = 1\\
4x - 3y = 3
\ end {array}\ right.\)
Paso 1: Vamos a resolver la ecuación (1) para\(y\).
\ (\ begin {alineado}
3x + 2y &= 1\\
2y &= -3x + 1\\
y &=\ dfrac {-3} {2} x +\ dfrac {1} {2}
\ end {alineado}\)
Paso 2: Sustituir la expresión\(\dfrac{-3}{2}x + \dfrac{1}{2}\) por\(y\) en la ecuación (2).
\(4x - 3(\dfrac{-3}{2}x + \dfrac{1}{2}) = 3\)
Paso 3: Resolver la ecuación obtenida en el paso 2.
\ (\ begin {alineado}
4x - 3 (\ dfrac {-3} {2} x +\ dfrac {1} {2}) &= 3\ text {Multiplica ambos lados por la pantalla LCD,} 2\\
4x +\ dfrac {9} {2} x -\ dfrac {3} {2} &= 3\\
8x + 9x - 3 &= 6\
17x - 3 &= 6\\
17x &= 9\\
x &=\ dfrac {9} {17}
\ final {alineado}\)
Paso 4: Sustituir\(x = \dfrac{9}{17}\) a la ecuación obtenida en el paso 1,\(y = \dfrac{-3}{2}x + \dfrac{1}{2}\)
\ (y =\ dfrac {-3} {2} (\ dfrac {9} {17}) +\ dfrac {1} {2}\\
y =\ dfrac {-27} {34} +\ dfrac {17} {34} =\ dfrac {-10} {34} =\ dfrac {-5} {17}\).
Ahora tenemos\(x = \dfrac{9}{17}\) y\(y = \dfrac{-5}{17}\)\
Paso 5: La sustitución mostrará que estos valores de\(x\) y\(y\) verifican.
Paso 6: La solución es\((\dfrac{9}{17}, \dfrac{-5}{17})\)
Set de Práctica D
Resolver el sistema
\ (\ left\ {\ begin {array} {r}
9x - 5y = -4\\
2x + 7y = -9
\ end {array}\ right.\)
- Contestar
-
Estas líneas se cruzan en el punto\((−1,−1)\).
Ejercicios
Para los siguientes problemas, resolver los sistemas por sustitución.
\ (\ left\ {\ begin {array} {r}
3x + 2y = 9\\
y = -3x + 6
\ end {array}\ right.\)
- Contestar
-
\((1, 3)\)
\ (\ left\ {\ begin {array} {r}
5x - 3y = -6\\
y = -4x + 12
\ end {array}\ right.\)
\ (\ left\ {\ begin {array} {r}
2x + 2y = 0\\
x = 3y - 4
\ end {array}\ right.\)
\ (\ left\ {\ begin {array} {r}
9x - 5y = -4\\
2x + 7y = -9
\ end {array}\ right.\)
- Contestar
-
\((-1, 1)\)
\ (\ left\ {\ begin {array} {r}
3x + 5y = 9\\
x = 4y - 14
\ end {array}\ right.\)
\ (\ left\ {\ begin {array} {r}
-3x + y = -4\\
2x + 3y = 10
\ end {array}\ right.\)
- Contestar
-
\((2,2)\)
\ (\ left\ {\ begin {array} {r}
-4x + y = -7\\
2x + 5y = 9
\ end {array}\ right.\)
\ (\ izquierda\ {\ begin {array} {r}
6x - 6 = 18\\
x + 3y = 3
\ end {array}\ derecha.\)
- Contestar
-
\((4, -\dfrac{1}{3})\)
\ (\ left\ {\ begin {array} {r}
-x - y = 5\\
23x + y = 5
\ end {array}\ right.\)
\ (\ left\ {\ begin {array} {r}
-5x + y = 4\\
10x - 2y = -8
\ end {array}\ right.\)
- Contestar
-
Dependiente (misma línea)
\ (\ left\ {\ begin {array} {r}
x + 4y = 1\\
-3x - 12y = -1
\ end {array}\ right.\)
\ (\ left\ {\ begin {array} {r}
4x - 2y = 8\\
6x + 3y = 0
\ end {array}\ right.\)
- Contestar
-
\((1,−2)\)
\ (\ left\ {\ begin {array} {r}
2x + 3y = 12\\
2x + 4y = 18
\ end {array}\ right.\)
\ (\ left\ {\ begin {array} {r}
3x - 9y = 6\\
6x - 18y = 5
\ end {array}\ right.\)
- Contestar
-
inconsistente (líneas paralelas)
\ (\ left\ {\ begin {array} {r}
-x + 4y = 8\\
3x - 12y = 10
\ end {array}\ right.\)
\ (\ left\ {\ begin {array} {r}
x + y = -6\\
x - y = 4
\ end {array}\ right.\)
- Contestar
-
\((−1,−5)\)
\ (\ left\ {\ begin {array} {r}
2x + y = 0\\
x - 3y = 0
\ end {array}\ right.\)
\ (\ left\ {\ begin {array} {r}
4x - 2y = 7\\
y = 4
\ end {array}\ right.\)
- Contestar
-
\((\dfrac{15}{4}, 4)\)
\ (\ left\ {\ begin {array} {r}
x + 6y = 11\\
x = -1
\ end {array}\ right.\)
\ (\ left\ {\ begin {array} {r}
2x - 4y = 10\\
3x = 5y + 12
\ end {array}\ right.\)
- Contestar
-
\((−1,−3)\)
\ (\ left\ {\ begin {array} {r}
y + 7x + 4 = 0\\
x = -7y + 28
\ end {array}\ right.\)
\ (\ izquierda\ {\ begin {array} {r}
x + 4y = 0\\
x +\ dfrac {2} {3} y =\ dfrac {10} {3}
\ end {array}\ derecha.\)
- Contestar
-
\((4,−1)\)
\ (\ izquierda\ {\ begin {array} {r}
x = 24 - 5y\\
x -\ dfrac {5} {4} y =\ dfrac {3} {2}
\ end {array}\ derecha.\)
\ (\ left\ {\ begin {array} {r}
x = 11 - 6y\\
3x + 18y = -33
\ end {array}\ right.\)
- Contestar
-
inconsistente (líneas paralelas)
\ (\ izquierda\ {\ begin {array} {r}
2x +\ dfrac {1} {3} y = 4\\
3x + 6y = 39
\ end {array}\ derecha.\)
\ (\ izquierda\ {\ begin {array} {r}
\ dfrac {4} {5} x +\ dfrac {1} {2} y =\ dfrac {3} {10}\
\ dfrac {1} {3} +\ dfrac {1} {2} y =\ dfrac {-1} {6}
\ end {array}\ derecha.\)
- Contestar
-
\((1,−1)\)
Ejercicios para revisión
Encuentra el cociente:\(\dfrac{x^2 - x - 12}{x^2 - 2x - 15} \div \dfrac{x^2 - 3x - 10}{x^2 - 2x - 8}\)
- Contestar
-
\(\dfrac{(x-4)^2}{(x-5)^2}\)
Encuentra la diferencia:\(\dfrac{x + 2}{x^2 + 5x + 6} - \dfrac{x + 1}{x^2 + 4x + 3}\)
Simplificar\(-\sqrt{81x^8y^5z^4}\)
- Contestar
-
\(-9x^4y^2z^2 \sqrt{y}\)
Usa la fórmula cuadrática para resolver\(2x^2 + 2x - 3 = 0\)
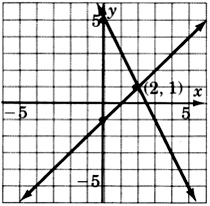
Resuelve graficando:
\ (\ left\ {\ begin {array} {r}
x - y = 1\\
2x + y = 5
\ end {array}\ right.\)
- Contestar
-
\((2,1)\)