11.4: Eliminación por Suma
- Page ID
- 112192
Las propiedades utilizadas en el método de adición
Otro método para resolver un sistema de dos ecuaciones lineales en dos variables se llama el método de eliminación por adición. Es similar al método de eliminación por sustitución en que el proceso elimina una ecuación y una variable. El método de eliminación por adición hace uso de las siguientes dos propiedades.
Si\(A, B\), y\(C\) son expresiones algebraicas tales que
\(A = B\)y\(C = D\)
Entonces:\(A + C = B + D\)
\(ax + (-ax) = 0\)
La propiedad 1 establece que si sumamos los lados izquierdos de dos ecuaciones juntos y los lados derechos de las mismas dos ecuaciones juntos, las sumas resultantes serán iguales. A esto lo llamamos ecuaciones sumadoras. La propiedad 2 establece que la suma de dos opuestos es cero.
El método de adición
Para resolver un sistema de dos ecuaciones lineales en dos variables por suma,
- Escribir, si es necesario, ambas ecuaciones en forma general,\(ax+by=c\).
- Si es necesario, multiplique una o ambas ecuaciones por factores que producirán coeficientes opuestos para una de las variables.
- Sumar las ecuaciones para eliminar una ecuación y una variable.
- Resolver la ecuación obtenida en el paso 3.
- Haga una de las siguientes acciones:
(a) Sustituir el valor obtenido en el paso 4 en cualquiera de las ecuaciones originales y resolver para obtener el valor de la otra variable,
o
(b) Repita los pasos 1-5 para la otra variable. - Consulta las soluciones en ambas ecuaciones.
- Escribe la solución como un par ordenado.
El método de adición funciona bien cuando el coeficiente de una de las variables es 1 o un número distinto de 1.
Conjunto de Muestras A
Resolver el sistema
\ (\ left\ {\ begin {array} {r}
x-y = 2\\
3x + y = 14
\ end {array}\ right.\)
Paso 1: Ambas ecuaciones aparecen en la forma adecuada.
Paso 2: Los coeficientes de ya\(y\) son opuestos,\(1\) y\(-1\), así no hay necesidad de una multiplicación.
Paso 3: Sumar las ecuaciones.
\ (\ begin {array} {c}
x-y=2\\
3 x+y=14\\
\ hline 4 x+0=16
\ end {array}\)
Paso 4: Resolver la ecuación\(4x = 16\)
\ (4x = 16\\
x = 4\)
El problema aún no está resuelto; todavía necesitamos el valor de\(y\).
Paso 5: Sustituir\(x = 4\) en cualquiera de las ecuaciones originales. Usaremos la ecuación 1.
\ (\ begin {aligned}
4 - y &= 2 &\ text {Resolver para} y\\
-y &= -2\\
y &= 2
\ end {alineado}\)
Ahora tenemos\(x = 4, y = 2\).
Paso 6: Sustituir\(x = 4\) y\(y = 2\) en ambas ecuaciones originales para una comprobación.
(1)
\ (\ begin {aligned}
x - y &= 2\\
4 - 2 &= 2\ text {¿Es esto correcto? }\\
2 &= 2\ text {Sí, esto es correcto.}
\ end {alineado}\)
(2)
\ (\ begin {aligned}
3x + y &= 14\\
3 (4) + 2 &= 14\\
12 + 2 &= 14\\
14 &= 14\ text {Sí, esto es correcto.}
\ end {alineado}\)
Paso 7: La solución es\((4, 2)\).
Las dos líneas de este sistema se cruzan en\((4, 2)\).
Conjunto de práctica A
Resuelve cada sistema por adición.
\ (\ left\ {\ begin {array} {r}
x + y = 6\\
2x - y = 0
\ end {array}\ right.\)
- Contestar
-
\((2, 4)\)
Resolver el sistema
\ (\ left\ {\ begin {array} {r}
x + 6y = 8\\
-x - 2y = 0
\ end {array}\ right.\)
- Contestar
-
\((-4, 2)\)
Conjunto de Muestras B
Resuelve los siguientes sistemas usando el método de adición.
Resolver
\ (\ left\ {\ begin {array} {r}
x + y = 6\\
2x - y = 0
\ end {array}\ right.\)
Paso 1: Las ecuaciones ya están en la forma adecuada,\(ax + by = c\)
Paso 2: Si multiplicamos la ecuación (2) por\(-3\), el coeficiente de\(a\) será opuestos y se volverá\(0\) al sumar, eliminando así\(a\).
\ (\ left\ {\ begin {array} {l}
{6 a - 5 b = 1 4}\\
{- 3 (2 a + 2 b) = - 3 (1 0)}
\ end {array}\ right tarrow\ left\ {\ begin {array} {l}
6 a-5 b=14\
-6 a-6 b=30
\ end {array}\ right. \ derecho.\)
Paso 3: Sumar las ecuaciones.
\ (\ begin {array} {c}
6a - 5b = 14\\
-6a - 6b = 30\\
\ hline 0 - 11b = 44
\ end {array}\)
Paso 4: Resolver la ecuación\(-11b = 44\)
\ (-11b = 44\\
b = -4\)
Paso 5: Sustituto\(b = -4\)
\ (\ begin {alineado}
2a + 2b &= -10\\
2a + 2 (-4) &= -10\ texto {Resolver para} a\\
2a - 8 &= -10\\
2a &= -2\\
a &= -1
\ end {alineado}\)
Ahora tenemos\(a = -1\) y\(b = -4\).
Paso 6: Sustituir\(a = -1\) y\(b = -4\) en ambas ecuaciones originales para una comprobación.
(1)
\ (\ begin {alineado}
6a - 5b &= 14\\
6 (-1) - 5 (-4) &= 14\\
-6 + 20 &= 14\\
14 &= 14\ text {Sí, esto es correcto.}
\ end {alineado}\)
(2)
\ (\ begin {alineado}
2a + 2b &= -10\\
2 (-1) + 2 (-4) &= -10\\
-2 - 8 &= -10
-10 &= -10\ text {Sí, esto es correcto.}
\ end {alineado}\)
Paso 7: la solución es\((-1, -4)\).
\ (\ left\ {\ begin {array} {r}
x + y = 6\\
2x - y = 0
\ end {array}\ right.\)
Paso 1: Reescribir el sistema en la forma adecuada.
\ (\ left\ {\ begin {array} {r}
3x + 2y = -4\\
4x - 5y = 10
\ end {array}\ right.\)
Paso 2: Dado que los coeficientes de\(y\) ya tienen signos opuestos, vamos a eliminar\(y\).
Multiplicar la ecuación (1) por\(5\), el coeficiente de\(y\) en la ecuación 2.
Multiplicar la ecuación (2) por\(2\), el coeficiente de\(y\) en la ecuación 1.
\ (\ left\ {\ begin {array} {l}
{5 (3 x + 2 y) = 5 (- 4)}\\
{2 (4 x - 5 y) = 2 (1 0)}
\ end {array}\ rightarrow\ left\ {\ begin {array} {l}
15 x+10 y=-20\
8 x-10 y=20
\ end {array}\ right. \ derecho.\)
Paso 3: Sumar las ecuaciones.
\ (\ begin {array} {c}
15x + 10y = -20\\
8x - 10y = 20\
\ hline 23x + 0 = 0
\ end {array}\)
Paso 4: Resolver la ecuación\(23x = 0\)
\ (23x = 0\\
x = 0\)
Paso 5: Sustituir\(x = 0\) en cualquiera de las ecuaciones originales. Usaremos la ecuación 1.
\ (\ begin {alineado}
3x + 2y &= -4\\
3 (0) + 2y &= -4\ text {Resolver para} y\\
0 + 2y &= -4\\
y &= -2
\ end {alineado}\)
Paso 6: La sustitución mostrará que estos valores verifican.
Paso 7: La solución es\((0, -2)\)
Set de práctica B
Resuelve cada uno de los siguientes sistemas usando el método de adición.
\ (\ left\ {\ begin {array} {r}
3x + y = 1\\
5x + y = 3
\ end {array}\ right.\)
- Contestar
-
\((1, -2)\)
\ (\ left\ {\ begin {array} {r}
x + 4y = 1\\
x - 2y = -5
\ end {array}\ right.\)
- Contestar
-
\((-3, 1)\)
\ (\ left\ {\ begin {array} {r}
2x + 3y = -10\\
-x + 2y = -2
\ end {array}\ right.\)
- Contestar
-
\((-2, -2)\)
\ (\ left\ {\ begin {array} {r}
5x - 3y = 1\\
8x - 6y = 4
\ end {array}\ right.\)
- Contestar
-
\((-1, -2)\)
\ (\ left\ {\ begin {array} {r}
3x - 5y = 9\\
4x + 8y = 12
\ end {array}\ right.\)
- Contestar
-
\((3, 0)\)
Suma y líneas paralelas o coincidentes
Cuando las líneas de un sistema son paralelas o coincidentes, el método de eliminación produce resultados idénticos a los del método de eliminación por sustitución.
Si los cálculos eliminan todas las variables y producen una contradicción, las dos líneas del sistema son paralelas y el sistema se denomina inconsistente.
Si los cálculos eliminan todas las variables y producen una identidad, las dos líneas del sistema son coincidentes y el sistema se llama dependiente.
Conjunto de Muestras C
Resolver
\ (\ left\ {\ begin {array} {r}
2x - y = 1\\
4x - 2y = 4
\ end {array}\ right.\)
Paso 1: Las ecuaciones están en la forma adecuada
Paso 2: Podemos eliminar\(x\) multiplicando la ecuación (1) por\(-2\).
\ (\ left\ {\ begin {array} {c}
{- 2 (2 x - y) = - 2 (1)}\\
{4 x - 2 y = 4}
\ end {array}\ quad\ rightarrow\ quad\ left\ {\ begin {array} {c}
-4 x+2 y=-2\\
4 x-2 y=4
\ end {array}\ right. \ derecho.\)
Paso 3: Añadir las ecuaciones
\ (\ begin {array} {c}
-4 x+2 y=-2\\
4 x-2 y=4\\
\ hline 0+0=2\\
0=2
\ end {array}\)
Esto es falso y, por tanto, es una contradicción. Las líneas de este sistema son paralelas. Este sistema es inconsistente.
Resolver
\ (\ left\ {\ begin {array} {r}
4x + 8y = 8\\
3x + 6y = 6
\ end {array}\ right.\)
Paso 1: Las ecuaciones están en la forma adecuada.
Paso 2: Podemos eliminar\(x\) multiplicando la ecuación (1) por\(-3\) y la ecuación (2) por\(4\).
\ (\ left\ {\ begin {array} {c}
{- 3 (4 x + 8 y) = - 3 (8)}\\
{4 (3 x + 6 y) = 4 (6)}
\ end {array}\ rightarrow\ left\ {\ begin {array} {c}
-12 x-24 y=-24\
12 x+24 y=24
\ end {array}\ right. \ derecho.\)
Paso 3: Sumar las ecuaciones.
\ (\ begin {array} {c}
-12x - 24y = -24\\
12x + 24y = 24\
\ hline 0 + 0 = 0\\
0=0
\ end {array}\)
Esto es cierto y es una identidad. Las líneas de este sistema son coincidentes.
Este sistema es dependiente.
Set de práctica C
Resuelve cada uno de los siguientes sistemas usando el método de adición.
\ (\ left\ {\ begin {array} {r}
-x + 2y = 6\\
-6x + 12y = 1
\ end {array}\ right.\)
- Contestar
-
inconsistente
\ (\ left\ {\ begin {array} {r}
4x - 28y = -4\\
x - 7y = -1
\ end {array}\ right.\)
- Contestar
-
dependiente
Ejercicios
Para los siguientes problemas, resolver los sistemas usando eliminación por adición.
\ (\ left\ {\ begin {array} {r}
x + y = 11\\
x - y = -1
\ end {array}\ right.\)
- Contestar
-
\((5, 6)\)
\ (\ left\ {\ begin {array} {r}
x + 3y = 13\\
x - 3y = - 11
\ end {array}\ right.\)
\ (\ left\ {\ begin {array} {r}
3x - 5y = -4\\
-4x + 5y = 2
\ end {array}\ right.\)
- Contestar
-
\((2, 2)\)
\ (\ left\ {\ begin {array} {r}
2x - 7y = 1\\
5x + 7y = -22
\ end {array}\ right.\)
\ (\ left\ {\ begin {array} {r}
-3x + 4y = -24\\
3x - 7y = 42
\ end {array}\ right.\)
- Contestar
-
\((0, -6)\)
\ (\ left\ {\ begin {array} {r}
8x + 5y = 3\\
9x - 5y = -71
\ end {array}\ right.\)
\ (\ left\ {\ begin {array} {r}
-x + 2y = -6\\
x + 3y = -4
\ end {array}\ right.\)
- Contestar
-
\((2, -2)\)
\ (\ left\ {\ begin {array} {r}
4x + y = 0\\
3x + y = 0
\ end {array}\ right.\)
\ (\ left\ {\ begin {array} {r}
x + y = -4\\
-x - y = 4
\ end {array}\ right.\)
- Contestar
-
dependiente
\ (\ left\ {\ begin {array} {r}
-2x - 3y = -6\\
2x + 3y = 6
\ end {array}\ right.\)
\ (\ izquierda\ {\ begin {array} {r}
3x + 4y = 7\\
x + 5y = 6
\ end {array}\ derecha.\)
- Contestar
-
\((1, 1)\)
\ (\ left\ {\ begin {array} {r}
4x - 2y = 2\\
7x + 4y = 26
\ end {array}\ right.\)
\ (\ left\ {\ begin {array} {r}
3x + y = -4\\
5x - 2y = -14
\ end {array}\ right.\)
- Contestar
-
\((-2, 2)\)
\ (\ left\ {\ begin {array} {r}
5x - 3y = 20\\
-x + 6y = -4
\ end {array}\ right.\)
\ (\ left\ {\ begin {array} {r}
6x + 2y = -18\\
-x + 5y = 19
\ end {array}\ right.\)
- Contestar
-
\((-4, 3)\)
\ (\ izquierda\ {\ begin {array} {r}
x - 11y = 17\\
2x - 22y = 4
\ end {array}\ derecha.\)
\ (\ left\ {\ begin {array} {r}
-2x + 3y = 20\\
-3x + 2y = 15
\ end {array}\ right.\)
- Contestar
-
\((-1, 6)\)
\ (\ left\ {\ begin {array} {r}
-5x + 2y = -4\\
-3x - 5y = 10
\ end {array}\ right.\)
\ (\ left\ {\ begin {array} {r}
-3x - 4y = 2\\
-9x - 12y = 6
\ end {array}\ right.\)
- Contestar
-
dependiente
\ (\ left\ {\ begin {array} {r}
3x - 5y = 28\\
-4x - 2y = -20
\ end {array}\ right.\)
\ (\ left\ {\ begin {array} {r}
6x - 3y = 3\\
10x - 7y = 3
\ end {array}\ right.\)
- Contestar
-
\((1, 1)\)
\ (\ left\ {\ begin {array} {r}
-4x + 12y = 0\\
-8x + 16y = 0
\ end {array}\ right.\)
\ (\ left\ {\ begin {array} {r}
3x + y = -1\\
12x + 4y = 6
\ end {array}\ right.\)
- Contestar
-
inconsistente
\ (\ left\ {\ begin {array} {r}
8x + 5y = -23\\
-3x - 3y = 12
\ end {array}\ right.\)
\ (\ left\ {\ begin {array} {r}
2x + 8y = 10\\
3x + 12y = 15
\ end {array}\ right.\)
- Contestar
-
dependiente
\ (\ left\ {\ begin {array} {r}
4x + 6y = 8\\
6x + 8y = 12
\ end {array}\ right.\)
\ (\ left\ {\ begin {array} {r}
10x + 2y = 2\\
-15x - 3y = 3
\ end {array}\ right.\)
- Contestar
-
inconsistente
\ (\ izquierda\ {\ begin {array} {r}
x +\ dfrac {3} {4} y = -\ dfrac {1} {2}\\
\ dfrac {3} {5} x + y = -\ dfrac {7} {5}
\ end {array}\ derecha.\)
\ (\ izquierda\ {\ begin {array} {r}
x +\ dfrac {1} {3} y =\ dfrac {4} {3}\\
-x +\ dfrac {1} {6} y =\ dfrac {2} {3}
\ end {array}\ derecha.\)
- Contestar
-
\((0, 4)\)
\ (\ left\ {\ begin {array} {r}
8x - 3y = 25\\
4x - 5y = -5
\ end {array}\ right.\)
\ (\ left\ {\ begin {array} {r}
-10x - 4y = 72\\
9x + 5y = 39
\ end {array}\ right.\)
- Contestar
-
\((-\dfrac{258}{7}, \dfrac{519}{7})\)
\ (\ left\ {\ begin {array} {r}
12x + 16y = -36\\
-10x + 12y = 30
\ end {array}\ right.\)
\ (\ left\ {\ begin {array} {r}
25x - 32y = 14\\
-50x + 64y = -28
\ end {array}\ right.\)
- Contestar
-
dependiente
Ejercicios para revisión
Simplifica y escribe\((2x^{-3}y^4)^5(2xy^{-6})^{-5}\) para que solo aparezcan exponentes positivos.
Simplificar\(\sqrt{8} + 3\sqrt{50}\).
- Contestar
-
\(17 \sqrt{2}\)
Resolver la ecuación radical\(\sqrt{2x + 3} + 5 = 8\)
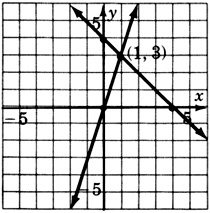
Resuelve graficando:
\ (\ left\ {\ begin {array} {r}
x + y = 4\\
3x - y = 0
\ end {array}\ right.\)
- Contestar
-
\((1, 3)\)
Resuelve usando el método de sustitución:
\ (\ left\ {\ begin {array} {r}
3x - 4y = -11\\
5x + y = -3
\ end {array}\ right.\)


