1.1: Enteros

Última actualización
Guardar como PDF

Page ID: 108444

Samar ElHitti, Marianna Bonanome, Holly Carley, Thomas Tradler, & Lin Zhou
CUNY New York City College of Technology & NYC College of Technology via New York City College of Technology at CUNY Academic Works

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Comenzamos con una breve revisión de la aritmética con enteros i.e.$\ldots,-3,-2,-1,0,1,2,3, \ldots$

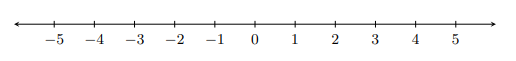
$clipboard_e27396619f1f16ac802dfddc2eb5b9e14.png$

Cualquier número tiene un peso y una señal.

La magnitud (o peso) de un número es la distancia que es desde 0 en la recta numérica.

Ejemplo 1.1

Por ejemplo, el peso de -5 es 5 y el peso de 7 es 7.

Dos números son opuestos si, en la recta numérica, están en lados opuestos de cero, pero a la misma distancia de cero.

Entonces, −5 es lo opuesto de 5, y 7 es lo opuesto a −7 y así sucesivamente.

Adición

Podemos sumar dos números con la ayuda de una línea numérica.

Ejemplo 1.2

Sumando dos números positivos: Por ejemplo para sumar$3 + 4$, comenzamos con 3 en la recta numérica y luego movemos 4 unidades a la derecha. Aterrizamos a las 7 que es nuestra respuesta.

$clipboard_eaa50e36932df7b766570bbd966c0b891.png$

Entonces,$3+4=7$. Observe que la respuesta tiene el mismo signo que los signos de 3 y 4 (ambos positivos) y su peso proviene de sumar los pesos de 3 y 4.

Siempre te mueves a la derecha cuando agregas un número positivo

Ejemplo 1.3

Sumando dos números negativos: Por ejemplo,$-10+(-4)$ significa que estás sumando una deuda de$\$ 4$ a una deuda ya existente de$\$ 10 .$ Entonces, comenzamos en -10 en la recta numérica y movemos 4 unidades a la izquierda, para aterrizar en$-14,$ lo que es la respuesta.

Siempre te mueves a la izquierda cuando agregas un número negativo (una deuda)

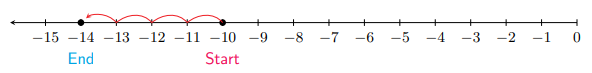
$clipboard_eee2362c20546ec074bbf0b8b3adda4da.png$

Entonces,$-10+(-4)=-14$. Observe que la respuesta tiene el mismo signo que los signos de -10 y -4 (ambos negativos) y su peso proviene de sumar los pesos de -10 y -4

Para sumar números de signos opuestos, es decir, un número positivo y otro negativo, también podemos usar la recta numérica. Por ejemplo, para realizar$10+(-4),$ comenzamos en 10 en la recta numérica y luego movemos 4 unidades hacia la izquierda. Aterrizamos en$6,$ lo que es la respuesta. Piense en$10+(-4)$ como tener$\$ 10$ y agregar una$\$ 4$ deuda. Porque estamos sumando una deuda, ¡nos movemos a la izquierda en la recta numérica!

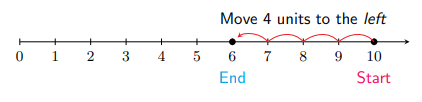
$clipboard_e5f26f5be4b0d41bdec3fe18706e5872a.png$

Entonces,$10+(-4)=6 .$ Observe que la respuesta tiene el mismo signo que el signo de 10 (positivo) porque es el número de mayor peso, y su peso viene de encontrar la diferencia de los pesos de 10 y -4

Observe que debido a que estábamos sumando dos números de signos opuestos, la respuesta terminó siendo la diferencia de peso (6) junto con el signo del número de mayor peso (positivo).

Ejemplo 1.4

Sumando dos números de signos opuestos: Por ejemplo,$3+(-7)$. Comenzamos a las 3 y nos movemos hacia 7 unidades a la izquierda, y aterrizamos en$-4,$ lo que es nuestra respuesta.

$clipboard_e1ba5d44ff12d55c3451665b676fcc295.png$

Entonces,$3+(-7)=-4 .$ Observe que la respuesta tiene el mismo signo que los signos de -7 (negativo) porque es el número de mayor peso, y su peso viene de encontrar la diferencia de los pesos de 3 y -7.

Ejemplo 1.5

Sumando opuestos: Comenzamos en -5 en la línea numérica y saltamos a la derecha 5 unidades para aterrizar finalmente en$0$. Entonces$-5+5=0$.

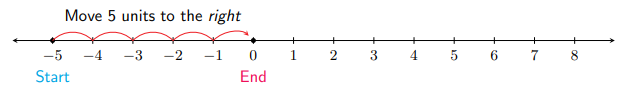
$clipboard_e85bc9d5c97ba98d476cda6c4a64a8492.png$

Nota 1.6

Dos números opuestos se llaman par cero, porque sumarlos siempre da como resultado 0.

Entonces, −5 y 5 son un par cero.

Adición de Intergers

Para sumar dos números del mismo letrero, agregue sus pesos y colóquelo después del letrero.
Para sumar dos números de signos opuestos, encuentra la diferencia de sus pesos y colócala después del signo del número con mayor peso.

Ejemplo 1.7

Agregar:

$-8+19=11$
$-8+4=-4$
$6+(-9)=-3$
$7+(-2)=5$
$(-4)+(-7)=-11$
$8+7=15$

Nota 1.8

Si bien podemos sumar en cualquier orden:$4+2=2+4$, a veces es conveniente sumar todos los números negativos y sumar todos los números positivos, y luego sumar los resultados. También hay momentos en los que es mejor notar ciertas simplificaciones si los números se agregan en un orden diferente.

Por ejemplo

\[-5+4+5+(-8)=-5+(-8)+4+5(\text { by reordering })\nonumber\]

entonces,

\[−5 + 4 + 5 + (−8) = −5 + (−8) + 4 + 5 = −13 + 9 = −4 \nonumber\]

También podríamos haber simplificado esto al señalar que (-5) y 5 son de par cero, por lo que nos quedamos con$4+(-8)$ lo que es -4.

Ejemplo 1.9

Podemos calcular

\[(-4)+(-5)+7+(-3)=(-4)+(-5)+(-3)+7=(-12)+7=-5\nonumber\]

Esto podríamos haber simplificado al señalar que (-4) y (-3) hacen -7, y -7 y 7 son pares cero, por lo que el total es -5.

Resta (como suma de lo opuesto)

Una vez que sabemos sumar números, estamos establecidos para restar números porque la resta no es más que suma de lo contrario. Es decir, restar 8 − 3 (que dice: restar 3 de 8) es lo mismo que 8 + (−3) (que dice: Sumando −3 a 8.).

Ejemplo 1.10

Entonces,$8-3=8+(-3),$ y, podemos usar las reglas de sumar dos números de signos opuestos para averiguar que la respuesta es También$5 .$ podemos usar la línea numérica. Empezamos a las 8 y nos movemos 3 unidades a la izquierda (sumar -3 es sumar una deuda, así que nos movemos hacia la izquierda). Así$8-3=5 .-4-3-2-1 0 1 2 3 4 5 6 7 8$ Fin Inicio Mover 3 unidades a la izquierda

Ejemplo 1.11

Para calcular$3-7$ primero lo reescribimos como un problema de suma. $3-7=3+(-7) .$Podemos usar la recta numérica, o las reglas de sumar dos números de signos opuestos. Y,$50,3-7=3+(-7)=-4$

Ejemplo 1.12

Para calcular$-4-1,$ primero lo reescribimos como un problema de suma. $-4-1=-4+(-1) .$Podemos usar la recta numérica, o las reglas de sumar dos números de los mismos signos. Si queremos usar las reglas, ambos números son negativos, por lo que nuestra respuesta será negativa, y, sumando los pesos de -4 y -1 es$5.50,-4-1=-4+(-1)=-5$

En la recta numérica, partimos en -4 y movemos 1 unidad a la izquierda, para aterrizar en -5 que es nuestra respuesta.

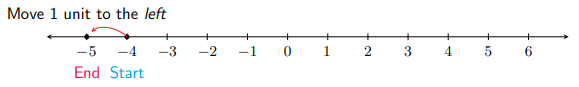
$clipboard_ef49f8d4826c75421c7da84c33f0e51ed.png$

Cambiar las restaciones a adiciones de esta manera es particularmente útil a la hora de sumar o restar varios números (porque podemos sumar en cualquier orden).

Ejemplo 1.13

$\begin{align*} & − 3 − 7 + 5 + 7 + 13 − 6 − (−9) \\ = & −3 + (−7) + 5 + 7 + 13 + (−6) + 9 \\ = & −3 + (−7) + (−6) + 5 + 7 + 13 + 9 \\ = & 18 \end{align*}$

$\begin{align*} & − 3 − 7 + 5 + 7 + 13 − 6 − (−9) \\ = & −3 + (−7) + 5 + 7 + 13 + (−6) + 9 \\ = & 5 + 13 \\ = & 18 \end{align*}$

Observación 1.14

Advertencia: El símbolo “-” se utiliza de dos maneras diferentes. Cuando está entre dos expresiones, significa restar (e.g.,$3-4$). De lo contrario, significa 'opuesto' o 'negativo' (e.g.,$-3+4$). Entonces en la expresión$-4-(-3)$, el primero y el último “-” significa opuesto y el que está en el medio significa restar. No se puede sobreestimar la importancia de entender esto.

Multiplicación y división de números positivos

La multiplicación de enteros es sumar en el sentido de que$3 \times 4=4+4+4$

Para multiplicar números más grandes, es mejor usar el esquema habitual de multiplicación. Por ejemplo:

Ejemplo 1.15

Multipliquemos 152 por 34. Por conveniencia, pondremos el número menor en la parte inferior (aunque no es necesario). Tenemos

\ (\ begin {array} {lllll}
& & & 1 & 5 & 2\
&\ &\ times & & & 3 & 4
\\ hline & & & 6 & 0 & 8\\
+ & 4 & 5 & 6 & 0\
\ hline & 5 & 1 & 6 & 8
\ end {array}\)

Y la división es lo opuesto a la multiplicación en el sentido de que computar$45 \div 9$ es encontrar un número para que cuando multiplicamos por 9 obtengamos 45. Corremos por nuestras tablas de multiplicación (que ojalá estén en nuestra cabeza) para descubrir que 5 hace el truco:$5 \times 9=45$ para que$45 \div 9=5 .$ Discutiremos la división desde un punto de vista diferente cuando discutamos fracciones.

Para dividir números más grandes, podemos usar división larga. Por ejemplo, dividamos 3571 por 11.

Ejemplo 1.16

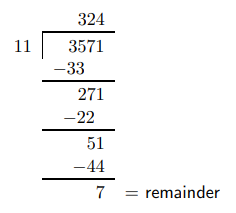
$clipboard_ed2fdc4ec400b113cc20c5b966357c36d.png$

Multiplicación con números negativos

La multiplicación es un poco difícil de entender sin la noción de distribución (discutida más adelante). Comenzaremos por señalar nuevamente lo que significa multiplicar un número por un número positivo: Entonces, si queremos computar$4 \cdot(-7)$ notamos

\[4 \cdot(-7)=(-7)+(-7)+(-7)+(-7)=-28\nonumber\]

Tenga en cuenta que ya que$4 \cdot 7=28,4 \cdot(-7)=-(4 \cdot 7) .$ podemos multiplicar números positivos en cualquier orden:$4 \cdot 7=7 \cdot 4$. Lo mismo ocurre con los números positivos y negativos:

\[(-7) \cdot 4=4 \cdot(-7)=-(4 \cdot 7)=-28\nonumber\]

Ejemplo 1.17

$5 \cdot(-12)=-(5 \cdot 12)=-60$y$(-3) \cdot(-2)=-(3 \cdot(-2))=-(-(3 \cdot 2))=6$

Ejemplo 1.18

Por lo que el tamaño del producto de dos números es el producto de sus tallas. El signo es positivo si los signos son los mismos y negativos si son diferentes.

Ejemplo 1.19

Dos cantidades una al lado de la otra, sin símbolo entre ellas (excepto paréntesis alrededor de uno o ambos números), tiene una multiplicación implícita. Por ejemplo,$3(2)=3 \times 2$.

Ejemplo 1.20

Multiplicar:

$(-5)(-8)=40$
$(-6) \cdot 7=-42$
$4 \cdot 12=48$
$(-3)(-6) \cdot 4(-3)=18 \cdot 4(-3)=72(-3)=-216(\text { multiplying from left to right })$
$(-3)(-5) \cdot 4(-2)=(-3) \cdot 4 \cdot(-5)(-2)=-12 \cdot 10=-120($ya que podemos multiplicar en cualquier orden es conveniente ver eso$-5 \cdot-2=10 .$)

Exponentes de enteros

Recordemos que un exponente positivo representa el número de veces que un número se multiplica por sí mismo.

Ejemplo 1.21

Evaluar:

$5^{2}=5 \cdot 5=25$
$(-4)^{3}=(-4) \cdot(-4) \cdot(-4)=16 \cdot(-4)=-64$
$(-7)^{1}=-7$
$-2^{4}=-2 \cdot 2 \cdot 2 \cdot 2=-16$Nota: ¡El exponente aquí es para 2 no para −2!
$(-3)^{4}=(-3) \cdot(-3) \cdot(-3) \cdot(-3)=9 \cdot(-3) \cdot(-3)=-27 \cdot(-3)=81$
$(-2)^{5}=(-2) \cdot(-2) \cdot(-2) \cdot(-2) \cdot(-2)=-32$

Las reglas del exponente en detalle serán discutidas más a fondo en el Capítulo 5.

División que involucra números negativos

La división es solo cuestión de conocer la multiplicación y por lo tanto tiene la misma regla: El tamaño del cociente de dos números es el cociente de los tamaños. El signo es positivo si los signos son los mismos y negativos si son diferentes.

Ejemplo 1.22

Dividir:

$(-42) \div 7=-6$
$81 \div(-9)=-9$
$(-35) \div(-7)=5$
$14 \div 2=7$
$0 \div 5=0$. Nota Al dividir 0 por cualquier número, la respuesta es siempre 0.
$-10 \div 0=$indefinido.

Nota 1.23

¡Cualquier número dividido por 0 no está definido!

Multiplicar y dividir enteros

Considera dos números a la vez.

Si los signos de los dos números son iguales, entonces el signo de la respuesta es positivo.
Si los signos de los dos números son diferentes, entonces el signo de la respuesta es negativo.