1.16: Trinomios de Factoraje y Factoraje Mixto

Factorización de Trinomios\(a x^{2}+b x+c\) por el Método AC

Sabemos que multiplicar dos binomios por el método FOIL da como resultado un polinomio de cuatro términos y en muchos casos se puede combinar en un polinomio de tres términos. Por ejemplo:

\[ \begin{align*} (x+3)(2 x+1) &=2 x^{2}+1 x+6 x+3 \\[4pt] &=2 x^{2}+7 x+3 . \end{align*}\]

Esto indica que si queremos factorizar la expresión\(2 x^{2}+7 x+3\), obtendremos un producto de dos binomios\((x+3)\) y\((2 x+1)\), es decir,

\[2 x^{2}+7 x+3=(x+3)(2 x+1). \nonumber\]

En esta sección, aprenderemos a revertir el procedimiento de FOIL para factorizar trinomios de la forma\(a x^{2}+b x+c \). El procedimiento se llama el método AC.

Método AC a factorizar\(a x^{2}+b x+c ; a \neq 0\)

• Paso 1. Encuentra el producto\(a c\), es decir, el producto de los coeficientes del primer y último término.
• Paso 2. Encuentra dos enteros cuyo producto es\(a c\) y cuya suma es\(b\). Si tal par entero no se puede encontrar, entonces el polinomio no puede ser factorizado.
• Paso 3. Utilice los dos enteros encontrados en el paso 2 para reescribir el término\(b x\) como una suma de dos términos.
• Paso 4. Factorizar por el método de agrupación.

Por ejemplo: Factor\(2 x^{2}+7 x+3\).

Paso\(1 \). El producto de\(a c\) es\(2 \cdot 3=6\).

Paso 2. Buscamos dos números cuyo producto sea 6 y cuya suma sea 7. Podemos hacer esto por inspección o escribiendo todos los pares de números cuyo producto es 6 y calcular la suma para cada par:\(1+6=7,2+3=5\). Entonces 1 y 6 son los números que estamos buscando.

Paso 3. Escribimos\(7 x=1 x+6 x\) así

\[2 x^{2}+7 x+3=2 x^{2}+x+6 x+3\nonumber\]

Paso 4.

\ [\ begin {align*}\ begin {aligned}
2 x^ {2} +x+6 x+3 &=\ left (2 x^ {2} +x\ right) + (6 x+3) ~~\ text {Factor por Agrupación}\\
&=x (2 x+1) +3 (2 x+1)\\
& =( x+3) (2 x+1)
\ end {alineado}\ end {align*}\ nonumber\]

Podemos verificar si factorizamos correctamente distribuyendo nuestra respuesta. Podemos usar el método FOIL aprendido previamente para verificar si los binomios factorizados nos dan el trinomio original\(2 x^{2}+7 x+3\).

Ejemplo\(\PageIndex{1}\)

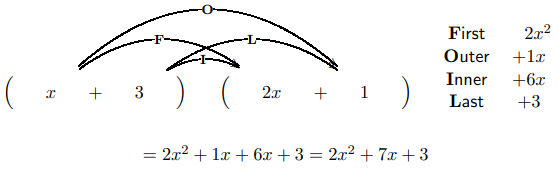
Factorizar el polinomio dado por el método AC.

a)\(2 x^{2}+15 x-27\)

• Paso 1. El producto de\(a c=(2)(-27)=-54\)
• Paso 2. Ahora necesitamos encontrar dos enteros cuyo producto es - 54. Podemos enumerar todas las posibilidades:

\[(-1)(54), \quad(-2)(27), \quad(-3)(18), \quad(-6)(9),\nonumber\]

\[(1)(-54), \quad(2)(-27), \quad(3)(-18), \quad(6)(-9)\nonumber\]

y calcular la suma de cada par. Sólo los enteros -3 y 18 suman 15.

• Paso 3. Podemos reescribir el término medio\(15 x=-3 x+18 x \). Entonces\(2 x^{2}+15 x-\)\(27=2 x^{2}-3 x+18 x-27\)
• Paso 4. Nosotros factorizamos por agrupación.

\ [\ begin {align*}
2 x^ {2} +15 x-27 &=2 x^ {2} -3 x+18 x-27\\
&=\ izquierda (2 x^ {2} -3 x\ derecha) + (18 x-27)\\
&=x (2 x-3) +9 (2 x-3)\\
& =( x+9) (2 x-3)
\ end {align*}\ nonumber\]

b)\(12 x^{2}-11 x+2:\)

Paso 1. El producto de\(a c=(12)(2)=24\)

Paso 2. Necesitamos encontrar dos enteros cuyo producto sea 24 y cuya suma sea -11. Enumeramos todos los pares de factores de 24:

\[(1)(24), \quad(2)(12), \quad(3)(8), \quad(4)(6)\nonumber\]

\[(-1)(-24), \quad(-2)(-12), \quad(-3)(-8), \quad(-4)(-6)\nonumber\]

El par -3 y -8 tendrá una suma -11.

Paso 3. Reescribimos el término medio\(-11 x=(-3 x)+(-8 x)\).

Paso 4. Entonces podemos terminar el factoring.

\ [\ begin {alinear*}
12 x^ {2} -11 x+2 &=12 x^ {2} -3 x+ (-8 x) +2\\
&=\ izquierda (12 x^ {2} -3 x\ derecha) + (-8 x+2)\\
&=3 x (4 x-1) + (-2) (4 x-1)\\
& =( 3 x-2) (4 x-1)
\ final {alinear*}\ nonumber\]

Tenga en cuenta que cuando reescribimos el término medio, lo escribimos como una suma (aunque el segundo término sea negativo). Esto es para poder agruparse sin preocuparse por la sustracción. ya que de lo contrario el paso de agrupación se vería así:

\[12 x^{2}-3 x-8 x+2=\left(12 x^{2}-3 x\right)-(8 x-2) \nonumber\]

(tenga en cuenta la resta de 2). También, tenga en cuenta que factorizamos (-2) en el segundo al último paso. Esto fue con el fin de asegurarse que ese\((4 x-1)\) era un factor común.

c)\(3 x^{2}+4 x-2\)

El producto de\(a c=(3)(-2)=-6\), y este número factores como:

\[(-1)(6), \quad(-2)(3), \quad(1)(-6), \quad(2)(-3)\nonumber\]

Es claro que ninguno de los pares de la lista dará una suma\(4 \). Esto significa que el polinomio\(3 x^{2}+4 x-2\) no se puede factorizar en dos binomios (usando enteros). Lo llamamos polinomio primo.

Factorización de Trinomios\(x^{2}+b x+c\)

En el caso especial cuando\(a=1\), el método AC aún funciona. Por ejemplo, para factorizar\(x^{2}-6 x+5\), primero calculamos\(a c=(1)(5)=5 \). Entonces necesitamos encontrar dos números cuyo producto es 5 y cuya suma es\(-6 \). desde\((-1)(-5)=5\) y\((-1)+(-5)=-6\), por el método de agrupación tenemos:

\ [\ begin {alinear*}
x^ {2} -6 x+5 &=x^ {2} -1 x+ (-5 x) +5\\
&=\ izquierda (x^ {2} -1 x\ derecha) + (-5 x+5)\\
&=x (x-1) + (-5) (x-1)\\
& =( x-5) (x-1)
\ end {alinear*}\ nonumber\]

Ahora vamos a observar el resultado. El resultado tiene la forma\((x+[-5])(x+[-1])\), y los dos números en las dos casillas son solo los dos números que obtenemos para reescribir el coeficiente del término medio\(-6\), es decir -1 y\(-5 \).

Este ejemplo muestra que para factorizar\(x^{2}+b x+c\), se puede simplificar el método de agrupación. Podemos escribir directamente la forma factorizada del polinomio una vez que conocemos los dos números que se multiplican\(a c\) y se suman a\(b\). Es decir,\(x^{2}+b x+c\) se factoriza como\((x+\square)(x+\square)\), siendo el producto de los dos números en las casillas\(a c=(1)(c)=c\) y siendo la suma de los dos números en las casillas\(b\),

Ejemplo 14.2

Factorizar el trinomio dado.

a)\(x^{2}+7 x+10\):

Tenemos que encontrar dos números cuyo producto es\(a c=c=10\), y cuya suma es\(7 \). El número 10 es un producto de los siguientes dos números:

\[(1)(10), \quad(2)(5), \quad(-1)(-10), \quad(-2)(-5)\nonumber\]

El par 2 y 5 da una suma\(7\), por lo tanto el trinomio se puede factorizar como:

\[x^{2}+7 x+10=(x+2)(x+5)\nonumber\]

b)\(t^{2}+4 t-12\):

Necesitamos encontrar dos números cuyo producto es\(a c=c=-12\) cuya suma es 4. El número -12 es un producto de los dos números siguientes:

\[(1)(-12), \quad(2)(-6), \quad(3)(-4)\nonumber\]

\[(-1)(12), \quad(-2)(6), \quad(-3)(4).\nonumber\]

El par -2 y 6 da una suma\(4\), por lo tanto el trinomio se puede factorizar como:

\[t^{2}+4 t-12=(t+(-2))(t+6)=(t-2)(t+6)\nonumber\]

c)\(x^{2}-3 x-24\):

Necesitamos encontrar dos números cuyo producto es\(a c=c=-24\) cuya suma es -3. El número -24 se puede factorizar como:

\[(1)(-24), \quad(2)(-12), \quad(3)(-8), \quad(4)(-6)\nonumber\]

\[(-1)(24), \quad(-2)(12), \quad(-3)(8), \quad(-4)(6).\nonumber\]

Dado que ninguno de los pares de la lista suma\(-3\), el trinomio no puede factorizarse como producto de dos binomios. Se trata de un polinomio primo.

Factoring Mixto

Hasta el momento, hemos explicado las técnicas básicas de factorización de polinomios. Aquí está la guía que podemos seguir para seleccionar el método correcto para factorizar un polinomio dado completamente.

Lineamientos para Factorizar Completamente un Polinomio

• Paso 1. Si es posible, factorizar el GCF de todos los términos.
• Paso 2. Contar el número de términos del polinomio: si el polinomio tiene dos términos, pruebe la fórmula de diferencia de dos cuadrados; si el polinomio tiene tres términos, pruebe el método AC; si el polinomio tiene cuatro términos, pruebe el método de agrupación.
• Paso 3. Verifique si los factores en sí pueden ser factorizados. Si la respuesta es sí, factorizarlos completamente usando los métodos del paso 2.

Ejemplo 14.3

Factorizar completamente el polinomio dado.

a)\(3 x^{2}-12\):

\ [\ begin {align*}
3 x^ {2} -12 &=3\ left (x^ {2} -4\ right)\ quad\ text {Facturar el GCF 3}\\
&=3 (x+2) (x+ (-2))\ quad\ text {Facturar la diferencia de dos cuadrados} x^2-4\\
&=3 (x+2) (x-2)
\ end {align*}\ umber\]

b)\(4 x^{3}-20 x^{2}+24 x\):

\ [\ begin {align*}
4 x^ {3} -20 x^ {2} +24 x &=4 x\ izquierda (x^ {2} -5 x+6\ derecha)\ quad\ text {Facturar el GCF} 4x\\
&=4 x (x+ (-2)) (x+ (-3))\ quad\ text {Factor el trinomio} x^ {2} -5 x+6\
&=4 x (x-2) (x-3)
\ final {alinear*}\ nonumber\]

c)\(-10 z^{2}-4 z+6\):

\ [\ begin {alinear*}
-10 z^ {2} -4 z+6 &=-2\ izquierda (5 z^ {2} +2 z-3\ derecha)\ quad\ text {Facturar lo opuesto del GCF} -2\\
&=-2\ izquierda (5 z^ {2} -3 z+5 z-3\ derecha)\ quad\ text {Factor el trinomio} 5 z^ {2} +2 z-3\\
&=-2\ izquierda [\ izquierda (5 z^ {2} -3 z\ derecha) + (5 z-3)\ derecha]\\ &=-2 [z (5 z-3) +1 (5 z-3)]\\ &=-2 (z+1) (5 z-3)
\ end {align*}\ nonumber\]

d)\(x^{3}-7 x^{2}-4 x+28\)

\ [\ begin {align*}
x^ {3} -7 x^ {2} -4 x+28 &=\ left (x^ {3} -7 x^ {2}\ right) + (-4 x+28)\ quad\ text {Factor por agrupación}\\
&=x^ {2} (x-7) + (-4) (x-7)\
&=\ izquierda (x^ {2}\ derecha -4) (x-7)\\ & =( x+2) (x+ (-2)) (x-7)\ cuádruple\ texto {Factor} x^ {2} -4\\ & =( x+2) (x-2) (x-7)
\ end {align*}\ nonumber\]

e)\(30 x^{2}+10 x^{4}-280\)

\ [\ begin {align*}
30 x^ {2} +10 x^ {4} -280 &=10 x^ {4} +30 x^ {2} -280\ quad\ text {Reordenar en potencias decrecientes de la variable}\\
&=10\ left (x^ {4} +3 x^ {2} -28\ derecha)\ quad\ text {Facturar el GCF} 10\\
&=10\ izquierda (y^ {2} +3 y-28\ derecha)\ quad\ texto {Escribir} y=x ^ {2}\ text {reconocer como una expresión cuadrática}\\ &=10 (y+7) (y-4)\\ &=10\ left (x^ {2} +7\ right)\ left (x^ {2} -4\ right)\ quad\ text {Reemplazar} y\ text {con} x^2\ text {y mira para ver si algo puede ser factor out}\\ &= 10\ izquierda (x^ {2} +7\ derecha) (x+2) (x-2)
\ final {alinear*}\ nonumber\]

Problema de salida

Factor completamente:\(8 x^{2}-10 x+3\)