4.4: Montaje de modelos lineales a datos
- Page ID
- 116981
Objetivos de aprendizaje
- Dibuja e interpreta diagramas de dispersión.
- Utilice una utilidad gráfica para encontrar la línea que mejor se ajuste.
- Distinguir entre relaciones lineales y no lineales.
- Ajustar una línea de regresión a un conjunto de datos y utilizar el modelo lineal para hacer predicciones.
Un profesor está intentando identificar tendencias entre los puntajes finales de los exámenes. Su clase tiene una mezcla de alumnos, por lo que se pregunta si existe alguna relación entre la edad y los puntajes finales de los exámenes. Una forma de analizar las puntuaciones es mediante la creación de un diagrama que relacione la edad de cada alumno con la puntuación del examen recibido. En esta sección, examinaremos uno de esos diagramas conocido como diagrama de dispersión.
Dibujar e interpretar gráficos de dispersión
Un gráfico de dispersión es un gráfico de puntos trazados que puede mostrar una relación entre dos conjuntos de datos. Si la relación es a partir de un modelo lineal, o de un modelo casi lineal, el profesor puede sacar conclusiones utilizando su conocimiento de las funciones lineales. La figura\(\PageIndex{1}\) muestra un diagrama de dispersión de la muestra.

Observe que este gráfico de dispersión no indica una relación lineal. Los puntos no parecen seguir una tendencia. Es decir, no parece haber relación entre la edad del alumno y la puntuación del examen final.
Ejemplo\(\PageIndex{1}\): Using a Scatter Plot to Investigate Cricket Chirps
La tabla muestra el número de chirps de cricket en 15 segundos, para varias temperaturas diferentes del aire, en grados Fahrenheit [1]. Trazar estos datos y determinar si los datos parecen estar relacionados linealmente.
| Chirps | 44 | 35 | 20.4 | 33 | 31 | 35 | 18.5 | 37 | 26 |
| Temperatura | 80.5 | 70.5 | 57 | 66 | 68 | 72 | 52 | 73.5 | 53 |
Solución
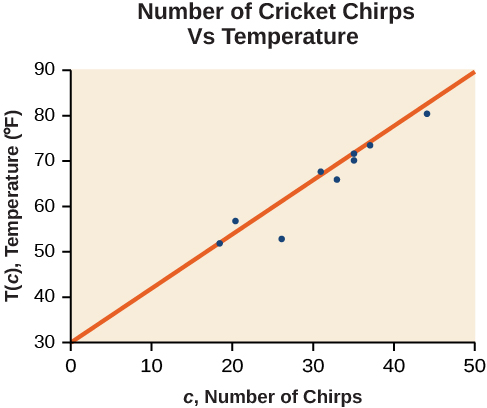
Trazar estos datos, como se representa en la Figura\(\PageIndex{2}\) sugiere que puede haber una tendencia. Podemos ver por la tendencia en los datos que el número de chirps aumenta a medida que aumenta la temperatura. La tendencia parece ser más o menos lineal, aunque ciertamente no perfectamente así.
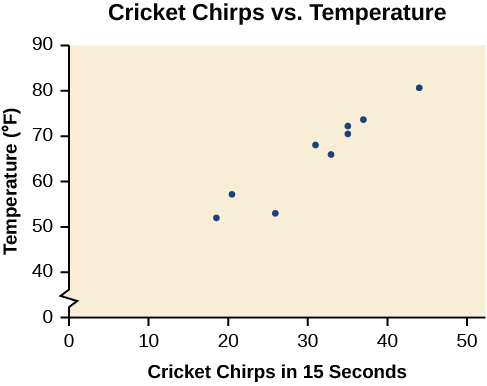
Encontrar la línea de mejor ajuste
Una vez que reconocemos la necesidad de una función lineal para modelar esos datos, la pregunta de seguimiento natural es “¿qué es esa función lineal?” Una forma de aproximar nuestra función lineal es esbozar la línea que parece que mejor se ajusta a los datos. Entonces podemos extender la línea hasta que podamos verificar la intercepción y. Podemos aproximar la pendiente de la línea extendiéndola hasta que podamos estimar la\(\frac{\text{rise}}{\text{run}}\).
Ejemplo\(\PageIndex{2}\): Finding a Line of Best Fit
Encuentra una función lineal que se ajuste a los datos\(\PageIndex{1}\) de la Tabla “mirando” una línea que parece encajar.
Solución
En una gráfica, podríamos intentar dibujar una línea.
Usando los puntos inicial y final de nuestra línea dibujada a mano, puntos\((0, 30)\) y\((50, 90)\), esta gráfica tiene una pendiente de
\[m=\dfrac{60}{50}=1.2\]
y una intercepción en Y a los 30. Esto da una ecuación de
\[T(c)=1.2c+30\]
donde\(c\) está el número de chirps en 15 segundos, y\(T(c)\) es la temperatura en grados Fahrenheit. La ecuación resultante se representa en la Figura\(\PageIndex{3}\).
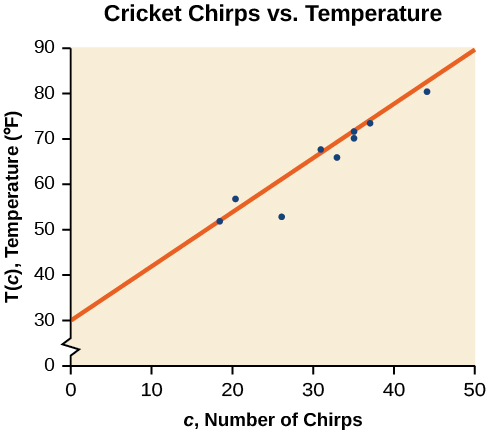
Análisis
Esta ecuación lineal puede entonces ser utilizada para aproximar respuestas a diversas preguntas que podríamos hacer sobre la tendencia.
Reconocimiento de interpolación o extrapolación
Si bien los datos para la mayoría de los ejemplos no caen perfectamente en la línea, la ecuación es nuestra mejor suposición sobre cómo se comportará la relación fuera de los valores para los que tenemos datos. Utilizamos un proceso conocido como interpolación cuando predecimos un valor dentro del dominio y rango de los datos. El proceso de extrapolación se utiliza cuando predecimos un valor fuera del dominio y rango de los datos.
La figura\(\PageIndex{4}\) compara los dos procesos para los datos de gricket-chirp abordados en Ejemplo\(\PageIndex{2}\). Podemos ver que la interpolación ocurriría si usáramos nuestro modelo para predecir la temperatura cuando los valores para chirps están entre 18.5 y 44. La extrapolación ocurriría si usáramos nuestro modelo para predecir la temperatura cuando los valores de los chirps son menores a 18.5 o mayores a 44.
Hay una diferencia entre hacer predicciones dentro del dominio y rango de valores para los que tenemos datos y fuera de ese dominio y rango. Predecir un valor fuera del dominio y rango tiene sus limitaciones. Cuando nuestro modelo ya no se aplica después de cierto punto, a veces se le llama desglose del modelo. Por ejemplo, predecir una función de costo para un periodo de dos años puede implicar examinar los datos donde la entrada es el tiempo en años y la salida es el costo. Pero si tratamos de extrapolar un costo cuando\(x=50\), es decir en 50 años, el modelo no aplicaría porque no podríamos dar cuenta de factores cincuenta años en el futuro.
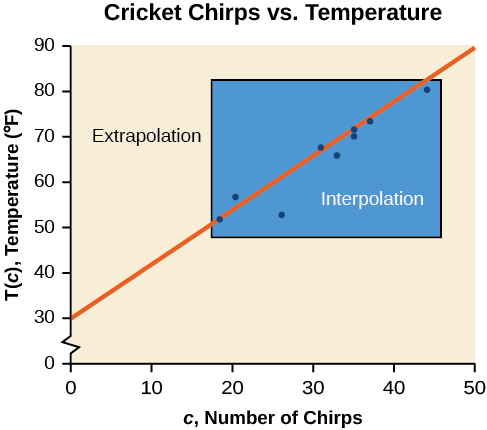
Interpolación y Extrapolación
Se utilizan diferentes métodos para hacer predicciones para analizar los datos.
- El método de extrapolación implica predecir un valor fuera del dominio y/o rango de los datos.
- La avería del modelo ocurre en el punto en que el modelo ya no se aplica.
Ejemplo\(\PageIndex{3}\): Understanding Interpolation and Extrapolation
Usa los datos de cricket de Table\(\PageIndex{1}\) para responder a las siguientes preguntas:
- ¿Predecir la temperatura cuando los grillos están gorjeando 30 veces en 15 segundos sería interpolación o extrapolación? Hacer la predicción, y discutir si es razonable.
- ¿Predecir el número de chirps que harán los grillos a 40 grados sería interpolación o extrapolación? Hacer la predicción, y discutir si es razonable.
Solución
a. El número de chirps en los datos proporcionados varió de 18.5 a 44. Una predicción a 30 chirps por 15 segundos está dentro del dominio de nuestros datos, por lo que sería la interpolación. Usando nuestro modelo:
\[\begin{align} T(30)&=30+1.2(30) \\ &=66 \text{ degrees} \end{align}\]
En base a los datos que tenemos, este valor parece razonable.
b. Los valores de temperatura variaron de 52 a 80.5. Predecir el número de chirps a 40 grados es extrapolación porque 40 está fuera del rango de nuestros datos. Usando nuestro modelo:
\[\begin{align} 40&=30+1.2c \\ 10&=1.2c \\ c&\approx8.33 \end{align}\]
Podemos comparar las regiones de interpolación y extrapolación usando la Figura\(\PageIndex{5}\).
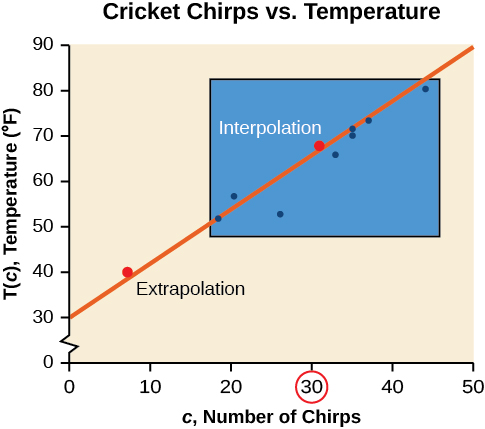
Análisis
Nuestro modelo predice que los grillos chirrían 8.33 veces en 15 segundos. Si bien esto podría ser posible, no tenemos ninguna razón para creer que nuestro modelo es válido fuera del dominio y rango. De hecho, generalmente los grillos dejan de gorjear por completo por debajo de alrededor de 50 grados.
Ejercicio\(\PageIndex{1}\)
Según los datos de Table\(\PageIndex{1}\), ¿qué temperatura podemos predecir que es si contamos 20 chirps en 15 segundos?
Solución
54°F
Encontrar la línea de mejor ajuste usando una utilidad gráfica
Si bien observar una línea funciona razonablemente bien, existen técnicas estadísticas para ajustar una línea a los datos que minimizan las diferencias entre la línea y los valores de datos [2]. Una de esas técnicas se llama regresión de mínimos cuadrados y puede ser calculada por muchas calculadoras gráficas, software de hojas de cálculo, software estadístico y muchas calculadoras basadas en la web [3]. La regresión de mínimos cuadrados es una media para determinar la línea que mejor se ajusta a los datos, y aquí nos referiremos a este método como regresión lineal.
![]() Dados los datos de entrada y las salidas correspondientes de una función lineal, encuentre la línea de mejor ajuste usando regresión lineal.
Dados los datos de entrada y las salidas correspondientes de una función lineal, encuentre la línea de mejor ajuste usando regresión lineal.
- Ingresa la entrada en la Lista 1 (L1).
- Ingrese la salida en la Lista 2 (L2).
- En una utilidad gráfica, seleccione Regresión lineal (LinReg).
Ejemplo\(\PageIndex{4}\): Finding a Least Squares Regression Line
Encuentra la línea de regresión de mínimos cuadrados usando los datos de gricket-chirp en la Tabla\(\PageIndex{1}\).
Solución
Ingresa la entrada (chirps) en la Lista 1 (L1).
Ingresa la salida (temperatura) en la Lista 2 (L2). Ver Tabla\(\PageIndex{2}\).
| L1 | 44 | 35 | 20.4 | 33 | 31 | 35 | 18.5 | 37 | 26 |
| L2 | 80.5 | 70.5 | 57 | 66 | 68 | 72 | 52 | 73.5 | 53 |
En una utilidad gráfica, seleccione Regresión lineal (LinReg). Usando los datos de chirrido de cricket anteriores, con la tecnología obtenemos la ecuación:
\[T(c)=30.281+1.143c\]
Análisis
Observe que esta línea es bastante similar a la ecuación que “miramos” pero debería ajustarse mejor a los datos. Observe también que el uso de esta ecuación cambiaría nuestra predicción de la temperatura al escuchar 30 chirps en 15 segundos de 66 grados a:
\[\begin{align} T(30)&=30.281+1.143(30) \\ &=64.571 \\ &\approx 64.6 \text{ degrees} \end{align}\]
La gráfica de la gráfica de dispersión con la línea de regresión de mínimos cuadrados se muestra en la Figura\(\PageIndex{6}\).
![]() ¿Alguna vez habrá un caso en el que dos líneas diferentes sirvan como la mejor opción para los datos?
¿Alguna vez habrá un caso en el que dos líneas diferentes sirvan como la mejor opción para los datos?
No. Solo hay una línea de mejor ajuste.
Distinguir entre modelos lineales y no lineales
Como vimos anteriormente con el modelo de gricket-chirp, algunos datos muestran fuertes tendencias lineales, pero otros datos, como los puntajes finales de los exámenes trazados por edad, son claramente no lineales. La mayoría de las calculadoras y los programas informáticos también pueden proporcionarnos el coeficiente de correlación, que es una medida de qué tan cerca se ajusta la línea a los datos. Muchas calculadoras gráficas requieren que el usuario encienda una selección de “diagnóstico” para encontrar el coeficiente de correlación, que los matemáticos etiquetan como\(r\). El coeficiente de correlación proporciona una manera fácil de tener una idea de qué tan cerca de una línea caen los datos.
Deberíamos calcular el coeficiente de correlación solo para datos que siguen un patrón lineal o para determinar el grado en que un conjunto de datos es lineal. Si los datos presentan un patrón no lineal, el coeficiente de correlación para una regresión lineal no tiene sentido. Para tener una idea de la relación entre el valor de\(r\) y la gráfica de los datos, la Figura\(\PageIndex{7}\) muestra algunos conjuntos de datos grandes con sus coeficientes de correlación. Recuerde, para todas las parcelas, el eje horizontal muestra la entrada y el eje vertical muestra la salida.
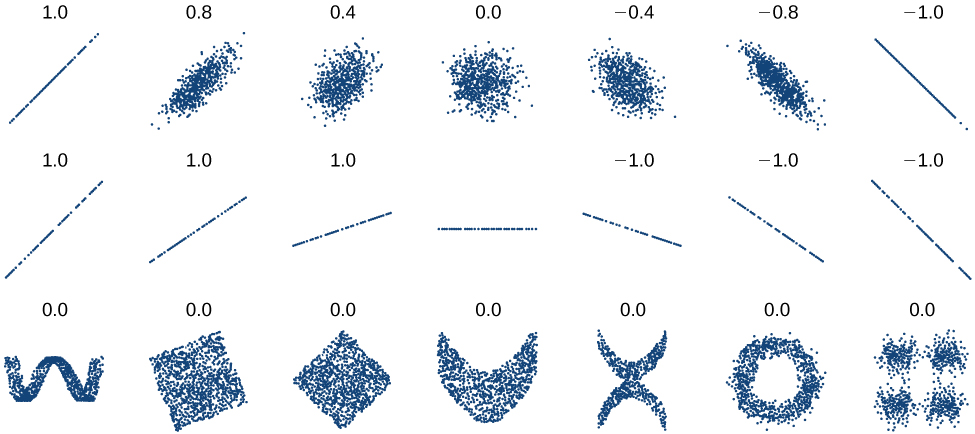
Coeficiente de Correlación
El coeficiente de correlación es un valor,\(r\), entre —1 y 1.
- \(r>0\)sugiere una relación positiva (creciente)
- \(r<0\)sugiere una relación negativa (decreciente)
- Cuanto más cerca esté el valor de 0, más dispersos serán los datos.
- Cuanto más cerca esté el valor de 1 o —1, menos dispersos estarán los datos.
Ejemplo\(\PageIndex{5}\): Finding a Correlation Coefficient
Calcular el coeficiente de correlación para los datos de gricket-chirp en la Tabla\(\PageIndex{1}\).
Solución
Debido a que los datos parecen seguir un patrón lineal, podemos usar la tecnología para calcular\(r\). Ingresa las entradas y salidas correspondientes y selecciona la Regresión Lineal. La calculadora también le proporcionará el coeficiente de correlación,\(r=0.9509\). Este valor es muy cercano a 1, lo que sugiere una fuerte relación lineal creciente.
Nota: Para algunas calculadoras, los Diagnósticos deben estar “encendidos” para obtener el coeficiente de correlación cuando se realiza una regresión lineal: [2nd] > [0] > [alpha] [x—1], luego desplácese hasta DIAGNOSTSON.
Predecir con una línea de regresión
Una vez que determinamos que un conjunto de datos es lineal usando el coeficiente de correlación, podemos usar la línea de regresión para hacer predicciones. Como aprendimos anteriormente, una línea de regresión es una línea que está más cerca de los datos en el gráfico de dispersión, lo que significa que solo una de esas líneas es la que mejor se ajusta a los datos.
Ejemplo\(\PageIndex{6}\): Using a Regression Line to Make Predictions
El consumo de gasolina en Estados Unidos ha ido en constante aumento. Los datos de consumo de 1994 a 2004 se muestran en la Tabla\(\PageIndex{3}\). Determinar si la tendencia es lineal y, de ser así, buscar un modelo para los datos. Utilizar el modelo para predecir el consumo en 2008.
| Año | '94 | '95 | '96 | '97 | '98 | '99 | '00 | '01 | '02 | '03 | '04 |
| Consumo (miles de millones de galones) | 113 | 116 | 118 | 119 | 123 | 125 | 126 | 128 | 131 | 133 | 136 |
El gráfico de dispersión de los datos, incluyendo la línea de regresión de mínimos cuadrados, se muestra en la Figura\(\PageIndex{8}\).
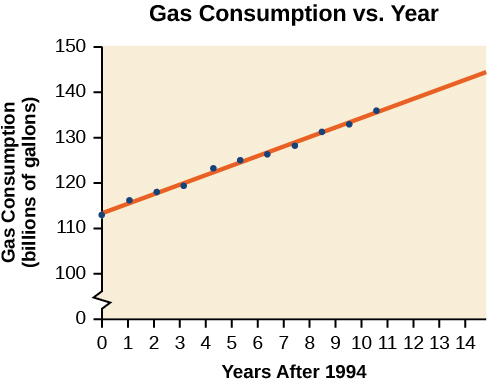
Podemos introducir nueva variable de entrada\(t\), que representa años desde 1994.
La ecuación de regresión de mínimos cuadrados es:
\[C(t)=113.318+2.209t\]
Utilizando la tecnología, se calculó que el coeficiente de correlación era de 0.9965, lo que sugiere una tendencia lineal creciente muy fuerte.
Utilizando esto para predecir el consumo en 2008\((t=14)\),
\[\begin{align} C(14)&=113.318+2.209(14) \\ &=144.244 \end{align}\]
El modelo predice 144.244 mil millones de galones de consumo de gasolina en 2008.
Ejercicio\(\PageIndex{1}\)
Utilice el modelo que creamos usando la tecnología en Ejemplo\(\PageIndex{6}\) para predecir el consumo de gas en 2011. ¿Es esto una interpolación o una extrapolación?
- Contestar
-
150.871 mil millones de galones; extrapolación
Conceptos clave
- Las gráficas de dispersión muestran la relación entre dos conjuntos de datos.
- Las gráficas de dispersión pueden representar modelos lineales o no lineales.
- La línea de mejor ajuste puede ser estimada o calculada, utilizando una calculadora o software estadístico.
- La interpolación se puede usar para predecir valores dentro del dominio y rango de los datos, mientras que la extrapolación se puede usar para predecir valores fuera del dominio y rango de los datos.
- El coeficiente de correlación,\(r\), indica el grado de relación lineal entre los datos.
- Una línea de regresión se ajusta mejor a los datos.
- La línea de regresión de mínimos cuadrados se encuentra minimizando los cuadrados de las distancias de puntos desde una línea que pasa por los datos y puede ser utilizada para hacer predicciones respecto a cualquiera de las variables.


