1.1: Conceptos básicos de enredos

Uno de los aspectos de la teoría del nudo que hace que los nudos sean desafiantes es que los nudos deben entenderse en su totalidad: no sobre la base de mirar solo algunos de sus cruces sino de ver cómo encajan todos esos cruces para pintar una imagen global del nudo. En definitiva, los invariantes de nudo que estudiamos más adelante en el semestre nos ayudarán a tomar esta perspectiva. Por ahora, sin embargo, sacaremos de escena las preguntas globales cortando nuestros nudos y fijando los extremos cortados, al igual que un entomólogo podría estudiar una mariposa montada. Los objetos que obtenemos para el estudio en este proceso se denominan enredos, y la clase de ellos que son más fáciles de estudiar son los llamados enredos racionales.

\(1.2.1\) Construyendo enredos racionales

Comenzamos pensando en enredos racionales como resultado de aplicar combinaciones de dos operaciones geométricas a una maraña horizontal “vacía”:

1. Giros de las hebras más a la derecha,\(T\text{,}\) y
2. Rotaciones de cuarto de vuelta de toda la maraña,\(R\text{.}\)

Entonces, por ejemplo, podríamos describir una maraña como una “palabra” construida a partir de estas letras como\[\text { TTRTTTRTTTTRTRT. }\]

Idealmente, lo que nos gustaría encontrar es una manera de representar cada una de estas operaciones como una operación que sucede a números racionales y no solo a enredos racionales. En este proceso lo que esperamos obtener es:

• Un grupo\(\Gamma\) de operaciones en enredos, y
• Una acción (derecha-) grupal de este grupo sobre los números racionales,\(\rho: \Gamma \rightarrow \operatorname{Func}(\mathbb{Q} \rightarrow \mathbb{Q})\).

Esta última definición podría ser nueva para ti, pero ojalá veamos con el ejemplo que es bastante natural. Para que sea preciso:

Definición\(1.2.1\) Group action.

Seamos\(G\) un grupo y\(S\) seamos un conjunto. Una acción (derecha) de\(G\) on\(S\) es una función\[\rho: G \rightarrow\{\text { bijections } S \rightarrow S\}\]

que respete la operación de grupo. Es decir, por todo\(g,h \in G\) lo que tenemos

1. \(\bigl( \rho(g) \circ \rho(h) \bigr)(x) = \bigl(\rho(h\cdot g)\bigr)(x)\)y
2. \(\bigl(\rho(g^{-1})\bigr)(x) = \bigl(\rho(g)\bigr)^{-1}(x).\)

En efecto, lo que hace una acción de grupo es asignar a cada elemento\(g\in G\) una función\(\rho(g) : S \to S\) invertible de tal manera que el producto de dos elementos\(h \cdot g \in G\) se asigna a la composición de las funciones\(\rho(g) \circ \rho(h) \text{.}\) La inversión de este orden es lo que hace de esta una acción correcta, y nos permite leer un producto de elementos de grupo como actuando de izquierda a derecha, por ejemplo, (girar, luego girar, luego girar, luego girar\ [\ begin {aligned}
T T R T R\\ flecha abajo\
\ r (t (t (t (t (t (t (t (t (x)))))
\ end {
alineado}\]

\(1.2.2\) Cómo opera el Grupo Tangle

Determinar la estructura del grupo de maraña nos ayudará a entender cómo pueden ser los enredos racionales después de que se haga todo el giro y rotación. Podemos observar cómo interactúa cada operación consigo misma:

1. Los giros iterados\(T, T^2, T^3, T^4, \ldots\) continúan agregando nuevos cruces y cambiando la maraña, por lo que\(T\) es un elemento de orden infinito en el grupo de maraña.
2. Las rotaciones iteradas se\(R, R^2, R^3, R^4,\ldots\) deshacen ellas mismas. Es fácil ver que como\(R\) es un cuarto de vuelta,\(R^4 = I\) será la identidad. Lo que es más sorprendente, y tardará\(1.3\) hasta Sección para entender, es que para enredos racionales, solo se necesitan dos rotaciones para volver a la identidad (\(R^2 = I\)). Así\(R\) es un elemento de orden 2 en el grupo de maraña.

El paso final es entender las inversas de cada una de estas operaciones básicas (generadores) en el grupo de maraña. Lo que queda claro del punto (2) anterior es que\(R\) es su propio inverso. Lo que es menos claro es cómo “destorcer un giro”, es decir, cómo construir un giro inverso usando solo más del mismo giro (combinado con posiblemente algunas rotaciones). El video de arriba hace la mejor justicia a la observación de que\[T \underbrace{R T R T R}_{T^{-1}}=I\]

y el descubrimiento de esta inversa completa nuestra presentación del grupo maraña.

Definición\(1.2.2\) Tangle group.

El grupo de maraña\(\Gamma\text{,}\) definido como el conjunto de todas las operaciones que llevan una maraña racional a otra, tiene la presentación\[\Gamma=\left\langle T, R \mid R^{2}=I=(T R)^{3}\right\rangle .\]

Cuando intentemos entender más concretamente a este grupo, podríamos intentar, como en el video anterior, examinar su acción sobre el conjunto de cuatro vértices de la maraña (las cuatro personas que sostienen las cuerdas). Esto sirve para representar cada operación de grupo maraña por la permutación que induce en las cuatro personas que sostienen las cuerdas. Pero no cuenta toda la historia porque, por ejemplo, la permutación inducida por el giro\(T\) has infinite order in the tangle group (where successive twists always compound on each other) but order two in the permutation group (which only looks at the fact that the two people holding the twisting ropes have returned back to their starting places after two twists).

\(1.2.3\) La acción del grupo Tangle sobre los números racionales

Lo que en última instancia queremos cuando determinamos una acción del grupo maraña sobre los números racionales es que la situación anterior no suceda: necesitamos que las funciones que operan sobre los números racionales reflejen toda la estructura revelada en la presentación de la Definición\(1.2.2\). Entonces lo que necesitamos son funciones\(t : \mathbb{Q}\to\mathbb{Q}\) y\(r : \mathbb{Q}\to\mathbb{Q}\) que satisfagan todos los siguientes.

1. \(t\)tiene orden infinito, es decir, nunca\(t^n(x) = t(t(t(\cdots t(x) \cdots )))\) debe igualar la función de identidad\(i(x) = x\) a menos que\(n=0\text{.}\)
2. \(r\)tiene orden dos, es decir,\(r^2(x) = r(r(x)) = i(x) = x\) para todos\(x\in\mathbb{Q}\text{.}\)
3. \((r\circ t)\)tiene orden tres, es decir,\((r\circ t)^3(x) = r(t(r(t(r(t(x)))))) = i(x)=x\) para todos\(x \in\mathbb{Q}\text{.}\)

Comenzando planteando que la función simple de “agregar uno”\(t(x) = x+1\) es una opción adecuada para representar la operación de orden infinito, luego\(T\text{,}\) vamos en busca de otra función\(r\) que es una “involución” (es decir, es igual a su propia función inversa) y que también interactúa con\(t\) in la manera especificada por (3) anterior. Encontramos que la función oposito-recíproca se ajusta milagrosamente a la factura, y llegar a una acción correcta de\(\Gamma\) sobre\(\mathbb{Q}\) definida por\[t(x)=x+1 \quad r(x)=-\frac{1}{x} .\]

El video anterior concluye con una explicación de cómo esto nos permite calcular un número racional, llamado el número de maraña, para una maraña racional una vez que asignamos a la maraña vacía el número 0.

\(1.2.4\) Ejercicios

Ejercicio\(1.2.4.1\).

Encuentre un ejemplo de diagrama de nudos con un número igual de cruces “sobre” como cruces “inferiores”, pero el nudo que representa no es anfiqueiral, es decir,\(K \neq -K\text{.}\)

Ejercicio\(1.2.4.2\).

(Adams, 2.12) Dibuja una secuencia de imágenes que demuestren que los siguientes dos enredos racionales son equivalentes.

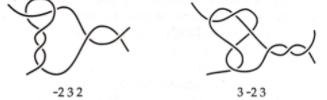
Figura 2.22 Dos enredos racionales equivalentes.

Ejercicio\(1.2.4.3\).

Encuentra un ejemplo de una maraña de 2 que no es una maraña racional, y explica cómo puedes decir que no es racional. (El texto de Adams y el papel Kauffman/Lambropoulou son buenos lugares para comenzar a buscar).