1.2: Aritmética de maraña
- Page ID
- 115841
Hasta el momento, nuestra estrategia para entender la estructura de los enredos racionales ha sido verlos como construidos a través de una serie de operaciones geométricas, giros y rotaciones, aplicadas a una maraña vacía. Pero eso no nos da una manera muy amigable de determinar el número de maraña para una maraña racional, ni (¡especialmente!) por ir en sentido contrario. Nuestro siguiente objetivo es encontrar una manera más sistemática de determinar el número de maraña de una maraña racional, que también es capaz de —igual de sistemáticamente, esperamos— determinar la maraña racional asociada a un número racional dado. Este sistema se construye sobre una nueva visión menos geométrica y más aritmética de cómo pueden definirse los enredos racionales.
\(1.3.1\) Aritmética, no Geometría
Más que pensar en enredos racionales como resultado de aplicar las operaciones geométricas de torcer y rotar (\(T\)y\(R\)) a una maraña vacía, lo que queremos en cambio es una forma de pensar sobre estas como operaciones de aritmética. Hacer eso requerirá que definamos lo que significa:
- Añadir dos enredos,\(G + H\text{,}\) y
- Multiplicar dos enredos,\(G*H\text{,}\)
tanto de una manera que se alinea con nuestras nociones geométricas originales y que tengan los efectos que esperamos en el número de maraña.
\(1.3.2\) Volteretas y Flypes: La Aritmética Invisible
La suma y la multiplicación son las operaciones maraña que “importan” en aritmética. En efecto, ahora definimos los enredos racionales como esos enredos que se pueden construir a través de la adición y multiplicación de los giros simples\([1]\) y\([-1]\) comenzando desde una maraña vacía.
Pero como la suma y la multiplicación no son en general conmutativas en los enredos (es decir, no siempre es cierto eso\(G + H \simeq H + G\) o aquello\(G*H \simeq H*G\)), ahora introducimos un nuevo conjunto de operaciones de maraña que no hacen diferencia a la aritmética, pero sí nos ayudan a sortear la falta de conmutatividad al permitir que volemos hacia la izquierda y los giros superiores para convertirlos a todos en giros a la derecha e inferior solamente.
\(1.3.3\) Fracciones continuas: El puente entre el enredo y el número
Como ahora sabemos que todos los enredos racionales se pueden construir únicamente usando giros a la derecha y al fondo, podemos determinar los efectos aritméticos de cada una de esas operaciones básicas. Si el número de maraña de\(G\) es\(x \in\mathbb{Q}\text{,}\) entonces
- Hacer un giro a la derecha agrega al número de enredo:\[G+[n] \rightsquigarrow x+n\]
y - Hacer un giro en la parte inferior conjuga esa suma con rotación, es decir, la recíproca. En otras palabras, hacer un giro inferior es lo mismo que tomar un recíproco, luego hacer un giro correcto (agregar), luego tomar el recíproco nuevamente:\[G * \frac{1}{[n]} \simeq \frac{1}{[n]+\frac{1}{G}} \rightsquigarrow \frac{1}{n+\frac{1}{x}}\]
Esto nos da el resultado clave de esta sección: que los enredos racionales, así como sus números de maraña, tienen cada uno representaciones (idénticas) como fracciones continuas.
Teorema\(1.3.1\) Continued Fraction Theorem.
Que\(G\) sea una maraña racional. Entonces\(G\) es equivalente (a través de flypes, movimientos de isotopía y/o movimientos de Reidemeister) a una maraña que tiene una representación de fracción continua\[G=\left[\left[a_{1}\right],\left[a_{2}\right],\left[a_{3}\right], \ldots,\left[a_{n}\right]\right]=\left[a_{1}\right]+\frac{1}{\left[a_{2}\right]+\frac{1}{\left[a_{3}\right]+\cdots+\frac{1}{1 a n]}}}\]
y el número de maraña (o fracción) de\(G\) tiene la misma expresión que un número racional:\[F(G)=\left[a_{1}, a_{2}, a_{3}, \ldots, a_{n}\right]=a_{1}+\frac{1}{a_{2}+\frac{1}{a_{3}+\cdots+\frac{1}{a_{n}}}} .\]
Además, ambas representaciones de fracciones continuas tienen una forma canónica en la que todos los enteros\(a_i\) tienen el mismo signo y la longitud\(n\) es impar.
\(1.3.4\) Uso de fracciones continuas para convertir enredos y números
El teorema\(1.3.1\) muestra que la representación fraccional continua (canónica) es nuestro puente entre los enredos racionales y los números racionales. Combinado con un algoritmo que podemos usar para calcular la representación canónica de fracción continua para cualquier\(x\in\mathbb{Q}\text{,}\) esto nos da todo lo que necesitamos para viajar entre mundos.
\(1.3.5\) Ejercicios
Ejercicio\(1.3.5.1\).
Esboza los enredos racionales\(T_1,T_2,T_3\) cuyos números de maraña (fracciones) son\(F(T_1)=4/5\text{,}\)\(F(T_2)=-5/8\text{,}\) y\(F(T_3)=9/2\text{.}\)
Ejercicio\(1.3.5.2\).
Para cada uno de los siguientes nudos\(K\text{,}\) encontrar y bosquejar una maraña racional\(T\) para la cual\(K = N(T)\) es el cierre numerador del boceto de\(T\text{.}\) Adams en el siguiente diagrama puede ser una inspiración:
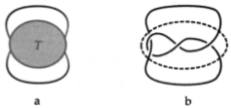
Figura 2.2.4 a) Un vínculo racional. b) El nudo figura-ocho.
- \(K = 3_1\text{,}\)el trébol.
- \(K = 4_1\text{,}\)la figura-ocho.
- \(K = 6_3\text{.}\)
Ejercicio\(1.3.5.3\).
Determina el número de enredos para cada uno de los enredos que encontraste en Ejercicio\(1.3.5.2\).
Ejercicio\(1.3.5.4\).
Consulte los dos enredos equivalentes de Ejercicio\(1.2.4.2\), que Adams anota como\ [T_ {1} =-232= [[2], [3], [-2]]\ quad\ text {y}\ quad T_ {2} =3-23= [[3], [-2], [3]]\)
Verificar que los números de maraña (fracciones) estén de acuerdo, es decir, que\(F(T_1) = F(T_2).\)
Ejercicio\(1.3.5.5\).
([KL] Lem. 5.3 y Lem. 6.3) Dejar\(\frac{p}{q} = [a_1,a_2,a_3,\ldots,a_n]\) ser un número racional escrito como fracción continuada.
- Demostrar que\([0,a_1,a_2,a_3,\ldots,a_n] = \frac{q}{p}\) representa su recíproco.
- Qué relación existe entre los enredos racionales\[T_{1}=\left[\left[a_{1}\right],\left[a_{2}\right],\left[a_{3}\right], \ldots,\left[a_{n}\right]\right] \quad \text { and } \quad T_{2}=\left[[0],\left[a_{1}\right],\left[a_{2}\right],\left[a_{3}\right], \ldots,\left[a_{n}\right]\right] ?\]
Explicar la relación usando imágenes, y en palabras explicar por qué esta relación no es sorprendente.


