4.1: De tríadas y ángulos de Euler a espinores. Una introducción heurística

Como ya se mencionó en la Sección 2.4.3, es una idea obvia enriquecer el formalismo álgebra Pauli introduciendo el complejo espacio vectorial\(\mathcal{V}(2, C)\) sobre el que operan las matrices. Los vectores complejos de dos componentes se llaman tradicionalmente espinores. Deseamos demostrar que dan lugar a una amplia gama de aplicaciones. De hecho, introduciremos el concepto spinor como respuesta natural a un problema que surge en el contexto del movimiento rotacional.

En la Sección 2 hemos considerado las rotaciones como operaciones realizadas en un espacio vectorial. Si bien este enfoque nos permitió dar una definición teórica grupal del campo magnético, un vector no es un constructo apropiado para dar cuenta de la rotación de un objeto orientable. El modelo matemático más simple adecuado para este propósito es un cartesiano (ortogonal) de tres marcos, brevemente, una tríada. El problema es considerar dos tríadas con orígenes coincidentes, y se describe la rotación del marco del objeto con respecto al marco espacial. Las tríadas se representan en términos de sus respectivos vectores unitarios: el marco espacial como\(\sum_{s} (\hat{x}_{1}, \hat{x}_{2}, \hat{x}_{3})\) y el marco de objeto como\(\sum_{s} (\hat{e}_{1}, \hat{e}_{2}, \hat{e}_{3})\). Aquí c significa “corpus”, ya que o para “objeto” parece ambiguo. Elegimos los marcos para ser diestros.

Estos objetos orientables no son puntuales, y su parametrización ofrece nuevos problemas. En este sentido podemos referirnos a las tríadas como “objetos superiores”, en contraste con los puntos que son “objetos inferiores”. El pensamiento que más fácil me viene a la mente es considerar los nueve cosenos de dirección\(\hat{e}_{i} \cdot \hat{x}_{k}\) pero esto es poco práctico, debido a las seis relaciones que conectan estos parámetros. Esta dificultad es eliminada por los tres ángulos eulerianos independientes, un conjunto de constructos muy ingeniosos, que nos dejan sin embargo con otro problema: estos parámetros no tienen buenas propiedades algebraicas; su conexión con el espacio vectorial euclidiano ordinario es proporcionada por relaciones bastante engorrosas. Esta dificultad final se resuelve con el concepto de espinor.

La teoría de la rotación de las tríadas se ha considerado generalmente en el contexto de la mecánica del cuerpo rígido Según la definición tradicional, un cuerpo rígido es “una colección de partículas puntuales que mantienen distancias rígidas”. Tal sistema no se presta a una generalización relativista útil Tampoco esta definición se reconcilia fácilmente con el principio de incertidumbre de Heisenberg.

Dado que la presente discusión tiene como objetivo aplicaciones a la relatividad y la mecánica cuántica, nos apresuramos a señalar que consideramos una tríada como un modelo matemático preciso para tratar objetos que son orientables en el espacio.

Si bien consideraremos brevemente la rotación del cuerpo rígido en la Sección 4.2, el concepto de rigidez en el sentido anteriormente definido no es esencial en nuestro argumento.

Pasamos ahora a un argumento heurístico que nos lleva de manera natural desde la rotación de la tríada hasta el concepto spinor.

Según el teorema de Euler cualquier desplazamiento de un cuerpo rígido fijado en un punto O equivale a una rotación alrededor de un eje a través de O. (Ver [Whi64], página 2.)

Este teorema proporciona la justificación para describir la configuración orientacional de\(\sum_{c}\) en términos de la matriz unitaria en\(\mathcal{SU}(2)\) que produce la configuración en cuestión a partir de la posición estándar en la que coinciden los dos marcos. Denotando las matrices unimodulares unitarias correspondientes a dos configuraciones por\(V_{1}, V_{2}\) una transición entre ellas es transportada por un operador U.

\[\begin{array}{c} {V_{2} = UV_{1}} \end{array} \label{EQ4.1.1}\]

Let

\[\begin{array}{c} {V = \cos\frac{\phi}{2}1-i \sin\frac{\phi}{2} \hat{v} \cdot \vec{\sigma}}\\ {= q_{0}1-i \vec{q} \cdot \vec{\sigma}} \end{array}\]

Aquí\(q_{0}, \vec{q}\) están los llamados componentes de cuaternión, ya que los\((-i \sigma_{k})\) obedecen a las reglas de conmutación de las unidades de cuaternión\(e_{k} : e_{1}e_{2} = -e_{2}e_{1} = e_{3}\). Tenemos

\[\begin{array}{c} {|V|=q_{0}^{2}+\vec{q}^2 = q_{0}^{2}+q_{1}^{2}+q_{2}^{2}+q_{3}^{2} = 1} \end{array} \label{EQ4.1.3}\]

A las Ecuaciones 4.1.1 - 4.1.3 se les puede dar una interpretación geométrica elegante:\(q_{0}, \vec{q}\) se consideran como las coordenadas de un punto en la unidad tridimensional hipersphere en el espacio de cuatro dimensiones\(\mathcal{V}(4, R)\). Así, la rotación de la tríada se mapea sobre la rotación de esta hiperesfera. La operación deja\ ref {EQ4.1.3} invariante.

El formalismo es el de la geometría elíptica, una contraparte de la geometría hiperbólica en el espacio Minkowski.

Esta geometría implica una “métrica”: la “distancia” de dos desplazamientos\(V_{1}\), y\(V_{2}\) se define como

\[\begin{array}{c} {\frac{1}{2} Tr(V_{2} \tilde{V}_{1}) = \cos \frac{\phi_{1}}{2} \cos \frac{\phi_{2}}{2}+\sin \frac{\phi_{1}}{2} \sin \frac{\phi_{2}}{2} \hat{v}_{1} \cdot \hat{v}_{2}} \end{array}\]

\[\begin{array}{c} {= \cos \frac{\phi}{2} = q_{10}q_{20}+\vec{q}_{1} \cdot \vec{q}_{2}} \end{array}\]

donde\(\phi\) es el ángulo de rotación que lleva\(V_{1}\), en\(V_{2}\). Obsérvese la analogía con la fórmula hiperbólica 2.4.67 en la Sección 2.4.3.

Tenemos aquí un ejemplo para un interesante principio de geometría: un “objeto superior” en un espacio inferior a menudo puede representarse como un “objeto inferior”, es decir, un punto en un espacio superior. El “objeto superior” es una tríada en el espacio ordinario\(\mathcal{V}(3, R)\). Se representa como un punto en el espacio superior\(\mathcal{V}(4, R)\).

Veremos que este principio es instrumental en la interpretación intuitiva de la mecánica cuántica. Los puntos en los espacios abstractos de esta teoría deben asociarse con objetos complejos en el espacio ordinario.

Si bien la representación del operador de rotación U y el objeto giratorio V en términos del mismo tipo de parametrización puede considerarse una fuente de elegancia matemática, también tiene una deficiencia. Los objetos rotativos pueden exhibir una orientación intrínseca preferida, como un eje de figura, o el espín electrónico, para lo cual no hay contraparte en las Ecuaciones\ ref {EQ4.1.1} y\ ref {EQ4.1.3}.

Esta situación es remediada por el siguiente artificio. Dejemos que el eje de la figura apunte a lo largo del vector unitario\(\hat{e}_{3}\) que coincide en la posición estándar con\(\hat{x}_{3}\) En lugar de generar la matriz de objeto V en términos de rotación única, consideramos que la siguiente secuencia estándar se lee de derecha a izquierda, (ver Figura 5.1):

\[\begin{array}{c} {U(\hat{x}_{3}, \frac{\alpha}{2}) U(\hat{x}_{2}, \frac{\beta}{2})U(\hat{x}_{3}, \frac{\gamma}{2}) = V(\alpha, \beta, \gamma)} \end{array} \label{EQ4.1.6}\]

Aquí\(\alpha, \beta, \gamma\) están los bien conocidos ángulos de Euler, y la secuencia de rotaciones es una de las variantes tradicionalmente utilizadas para su definición.

La notación requiere explicación. Continuaremos utilizando, como hicimos en la Sección 2,\(U(\hat{u}, \phi/2)\) para la matriz\(2 \times 2\) unitaria parametrizada en términos de variables de ángulo de eje. Llamaremos a esto también una parametrización uniaxial, para distinguirse de la parametrización biaxial de las matrices unitarias V en las que tanto la dirección espacial\(\hat{x}_{3}\), como el eje de la figura\(\hat{e}_{3}\), juegan un papel preferido.

En la Ecuación\ ref {EQ4.1.6} las rotaciones se definen a lo largo de los ejes especificados en el marco espacial\(\sum_{s}\). Sin embargo, en el transcurso de cada operación el eje se fija en ambos marcos. Por lo tanto, es simplemente cuestión de otro nombre (un alias I) describir la operación (4) en\(\sum_{c}\). Tenemos entonces para la misma matriz unitaria

\[\begin{array}{c} {V(\alpha, \beta, \gamma) = U(\hat{e}_{3}, \frac{\gamma}{2}) U(\hat{e}_{2}, \frac{\beta}{2})U(\hat{e}_{3}, \frac{\alpha}{2})} \end{array} \label{EQ4.1.7}\]

Obsérvese la inversión de la secuencia de operaciones que implican las rotaciones a e y, esta relación debe interpretarse en el sentido cinemático: el cuerpo se mueve desde la orientación inicial de coincidencia con\(\sum_{s}\) la posición final.

La equivalencia de\ ref {EQ4.1.6} y\ ref {EQ4.1.7} puede reconocerse por intuición geométrica, o también por transformaciones explícitas entre\(\sum_{s}\) y\(\sum_{c}\). (Véase [Got66], pág. 268).

En la literatura se suele considerar la secuencia

\[\begin{array}{c} {U(\hat{x}_{3}'', \frac{\gamma}{2}) U(\hat{x}_{2}', \frac{\beta}{2})U(\hat{x}_{3}, \frac{\alpha}{2})} \end{array}\]

donde\(\hat{x}_{2}'\), y\(\hat{x}_{3}''\) son posiciones de los ejes después del primer y segundo escalón respectivamente. Este procedimiento parece tener la incómoda propiedad de que las diferentes rotaciones se realizan en diferentes espacios. En una inspección más cercana, sin embargo, uno nota que la Ecuación 5.1.8 difiere solo en notación de la Ecuación\ ref {EQ4.1.7}. En la interpretación estática habitual\(\hat{e}_{1}, \hat{e}_{2}, \hat{e}_{3}\), se utiliza únicamente para la configuración final, y\(\hat{x}_{2}', \hat{x}_{3}''\) se introducen como ejes auxiliares. Si, por el contrario, se mira cinemáticamente el marco del objeto, se da cuenta de que en el instante de las rotaciones particulares coinciden los siguientes ejes:

\[\begin{array}{ccc} {\hat{x}_{3} = \hat{e}_{3}}&{ \hat{x}_{2}' = \hat{e}_{2}}&{\hat{x}_{3}'' = \hat{e}_{3}} \end{array}\]

Ahora escribimos la Ecuación\ ref {EQ4.1.6} explícitamente como

\[\begin{array}{c} {V(\alpha, \beta, \gamma) = U(\hat{e}_{3}, \frac{\gamma}{2}) U(\hat{e}_{2}, \frac{\beta}{2})U(\hat{e}_{3}, \frac{\alpha}{2})}\\ {= \begin{pmatrix} {e^{-i \alpha/2}}&{0}\\ {0}&{e^{i \alpha/2}} \end{pmatrix} \begin{pmatrix} {\cos(\beta/2)}&{-\sin(\beta/2)}\\ {\sin(\beta/2)}&{\cos(\beta/2)} \end{pmatrix} \begin{pmatrix} {e^{-i \gamma/2}}&{0}\\ {0}&{e^{i \gamma/2}} \end{pmatrix}}\\ {= \begin{pmatrix} {e^{-i \alpha/2} \cos(\beta/2) e^{-i \gamma/2}}&{-e^{-i \alpha/2} \cos(\beta/2) e^{i \gamma/2}}\\ {e^{i \alpha/2} \cos(\beta/2) e^{-i \gamma/2}}&{e^{i \alpha/2} \cos(\beta/2) e^{i \gamma/2}} \end{pmatrix}}\\ {= \begin{pmatrix} {\xi_{0}}&{-\xi_{1}^{*}}\\ {\xi_{1}}&{\xi_{0}^{*}} \end{pmatrix}} \end{array}\]

con

\[\begin{array}{c} {\xi_{0} = e^{-i \alpha/2} \cos(\beta/2) e^{-i \gamma/2}}\\ {\xi_{1} = e^{i \alpha/2} \cos(\beta/2) e^{i \gamma/2}} \end{array} \label{EQ4.1.11}\]

Los cuatro elementos de la matriz que aparecen en esta relación son los llamados parámetros Cayley-Klein. (Véase la Ecuación 2.4.43 en la Sección 2.4.2.)

Es una propiedad general de las matrices del álgebra\(\mathcal{A}_{2}\), que pueden representarse ya sea en términos de componentes o en términos de elementos de matriz. Hemos llegado a la conclusión de que la representación de una matriz unitaria en términos de elementos es adecuada para la parametrización de la configuración orientacional, mientras que el operador de rotación se representa en términos de componentes (variables de ángulo de eje).

Queda un paso más para expresar este resultado de la manera más eficiente. Presentamos los vectores complejos de dos componentes (espinores) de\(\mathcal{V}(2, C)\) ya mencionados al inicio del capítulo. En particular, definimos dos vectores de columna conjugados, o espinores ket:

\[\begin{array}{c} {|\xi \rangle = \begin{pmatrix} {\xi_{0}}\\ {\xi_{1}} \end{pmatrix}}\\ {|\bar{\xi} \rangle = \begin{pmatrix} {-\xi_{1}^{*}}\\ {\xi_{0}^{*}} \end{pmatrix}} \end{array}\]

y escribir simbólicamente la matriz V unitaria como

\[\begin{array}{c} {V = (\langle \xi |||\xi \rangle)} \end{array}\]

Definimos los vectores bra correspondientes dividiendo el conjugado hermitiano V horizontalmente en vectores de fila:

\[\begin{array}{c} {V^{\dagger} = \begin{pmatrix} {\xi_{0}^{*}}&{\xi_{1}^{*}}\\ {-\xi_{1}}&{\xi_{0}} \end{pmatrix} = \begin{pmatrix} {\langle \xi |}\\ {\langle \bar{\xi} |}\\ \end{pmatrix}} \end{array}\]

o

\[\begin{array}{cc} {\langle \xi | = (\xi_{0}^{*}, \xi_{1}^{*})}&{\langle \bar{\xi} | = (-\xi_{1}, \xi_{0})} \end{array}\]

La condición de unitariedad de V se puede expresar como

\[\begin{array}{c} {V^{\dagger}V = \begin{pmatrix} {\langle \xi |}\\ {\langle \bar{\xi} |} \end{pmatrix} (| \xi \rangle, |\bar{\xi} \rangle)} \end{array}\]

\[\begin{array}{c} {= \begin{pmatrix} {\langle \xi | \xi \rangle}&{\langle \xi | \bar{\xi} \rangle}\\ {\langle \bar{\xi} | \xi \rangle}&{\langle \bar{\xi} | \bar{\xi} \rangle} \end{pmatrix} = \begin{pmatrix} {1}&{0}\\ {0}&{1} \end{pmatrix}} \end{array}\]

cediendo a la vez las condiciones de ortonormalidad

\[\begin{array}{c} {\langle \xi | \xi \rangle = \langle \bar{\xi} | \bar{\xi} \rangle = 1}\\ {\langle \xi | \bar{\xi} \rangle = \langle \bar{\xi} | \xi \rangle} \end{array} \label{EQ4.1.18}\]

Estos pueden ser, por supuesto, verificados por cálculo directo. Los espinores ortogonales también se llaman espinores conjugados.

Vemos a partir de estas relaciones que nuestra definición de conjugación de espín es, en efecto, sensata. Sin embargo, el significado de este concepto es más rico de lo que podría sugerir la analogía con la relación orto-normalidad en el dominio real.

En primer lugar expresamos la conjugación de espín en términos de una operación matricial. La relación es no lineal, ya que implica la operación de conjugación compleja\(\mathcal{K}\)

Tenemos

\[\begin{array}{c} {| \bar{\xi} \rangle = \begin{pmatrix} {0}&{-1}\\ {1}&{0} \end{pmatrix} \mathcal{K} | \xi \rangle = -i \sigma_{2} \mathcal{K} | \xi \rangle} \end{array}\]

y

\[\begin{array}{c} {\langle \bar{\xi} | = \mathcal{K} \langle \xi | \begin{pmatrix} {0}&{1}\\ {-1}&{0} \end{pmatrix} = \mathcal{K} \langle \xi | i \sigma_{2}} \end{array}\]

Obtenemos de aquí

\[\begin{array}{cc} {| \bar{\bar{\xi}} \rangle = -| \xi \rangle}&{\langle \bar{\bar{\xi}} | = -\langle \xi |} \end{array} \label{EQ4.1.21}\]

La notación de barras para la conjugación de espín sugiere una conexión con la compleja reflexión del álgebra de Pauli. Veremos que efectivamente existe tal conexión. Sin embargo, hay que recordar que, a diferencia de la Ecuación\ ref {EQ4.1.21}, la reflexión compleja es involutiva, es decir, su iteración es la identidad\(\bar{\bar{A}} = A\).

La aparición del signo negativo en la Ecuación\ ref {EQ4.1.21} es una propiedad bien conocida de la función spin, sin embargo tenemos que diferir la discusión de este hecho intrigante para más adelante.

Ocasionalmente nos referiremos a los espinores normalizados según la Ecuación\ ref {EQ4.1.18} como espinores unitarios, para distinguirlos de los espinores relativistas normalizados como\(\langle \xi | \xi \rangle = k_{0}\) donde\(k_{0}\) está el 0-ésimo componente de un cuatro vector.

Echemos un vistazo más de cerca a la conexión entre las espinoras y las tríadas. En nuestro procedimiento heurístico iniciamos con una tríada objeto especificada por tres vectores unitarios ortonormales\(\hat{e}_{1}, \hat{e}_{2}, \hat{e}_{3}\) y llegamos a una especificación equivalente en términos de una espinora asociada\(| \xi \rangle\). Nuestra tarea es ahora partir del espinor y establecer la tríada correspondiente en términos de sus vectores unitarios. Esto se logra por medio de expresiones cuadráticas.

Consideramos que los llamados productos externos

\[\begin{array}{c} {| \xi \rangle \langle \xi | = \begin{pmatrix} {\xi_{0}}\\ {\xi_{1}} \end{pmatrix} (\xi_{0}^{*}, \xi_{1}^{*})}\\ {= \begin{pmatrix} {\xi_{0} \xi_{0}^{*}}&{\xi_{0} \xi_{1}^{*}}\\ {\xi_{1} \xi_{0}^{*}}&{\xi_{1} \xi_{1}^{*}} \end{pmatrix}} \end{array} \label{EQ4.1.22}\]

y

\[\begin{array}{c} {| \xi \rangle \langle \bar{\xi} | = \begin{pmatrix} {\xi_{0}}\\ {\xi_{1}} \end{pmatrix} (-\xi_{1}, \xi_{0})}\\ {= \begin{pmatrix} {-\xi_{0} \xi_{1}}&{\xi_{0}^{2}}\\ {-\xi_{1}^{2}}&{\xi_{0} \xi_{1}} \end{pmatrix}} \end{array} \label{EQ4.1.23}\]

que pueden considerarse como productos de a\(2 \times 1\) y\(1 \times 2\) matriz.

Para establecer la conexión con los vectores unitarios\(\hat{e}_{k}\), consideramos primero la configuración de la unidad en la que coinciden las tríadas:\(\alpha = \beta = \gamma = 0\), es decir,

\[\begin{array}{ccc} {\xi_{0} = 1, \xi_{1} = 0}&{or}&{| \xi \rangle = \begin{pmatrix} {1}\\ {0} \end{pmatrix}} \end{array}\]

con

\[\begin{array}{c} {| \bar{\xi} \rangle = \begin{pmatrix} {0}\\ {1} \end{pmatrix}} \end{array}\]

Denotando estas espinoras brevemente como\(|1 \rangle\) y\(|\bar{1} \rangle\) respectivamente, obtenemos de\ ref {EQ4.1.22} y\ ref {EQ4.1.23}

\[\begin{array}{c} {|1 \rangle \langle 1| = \begin{pmatrix} {1}&{0}\\ {0}&{0} \end{pmatrix} = \frac{1}{2}(1+\sigma_{3}) = \frac{1}{2}(1+\hat{x_{3}} \cdot \vec{\sigma})} \end{array} \label{EQ4.1.26}\]

\[\begin{array}{c} {|1 \rangle \langle \bar{1}| = \begin{pmatrix} {0}&{1}\\ {0}&{0} \end{pmatrix} = \frac{1}{2}(\sigma_{1}+i \sigma_{2}) = \frac{1}{2}(\hat{x_{1}}+i \hat{x_{2}}) \cdot \vec{\sigma}} \end{array} \label{EQ4.1.27}\]

Sea V la matriz unitaria que lleva el marco del objeto desde la posición de la unidad a\(\sum_{c} (\hat{e}_{1}, \hat{e}_{2}, \hat{e}_{3})\).

Desde\(V^{\dagger} = V^{-1}\) y\(\bar{V} = V\), tenemos

\[\begin{array}{cc} {V | 1 \rangle = | \xi \rangle}&{V | \bar{1} \rangle = | \bar{\xi} \rangle} \end{array}\]

\[\begin{array}{cc} {\langle 1 | V^{-1} = \langle \xi |}&{\langle \bar{1} | V^{-1} = \langle \bar{\xi} |} \end{array}\]

Al operar en\ ref {EQ4.1.26} y\ ref {EQ4.1.27} de izquierda y derecha por V y\(V^{-1}\) respectivamente, obtenemos

\[\begin{array}{c} {|1 \rangle \langle 1| = \frac{1}{2}(1+\hat{e_{3}} \cdot \vec{\sigma})} \end{array} \label{EQ4.1.30}\]

\[\begin{array}{c} {|1 \rangle \langle \bar{1}| =\frac{1}{2}(\hat{e_{1}}+i \hat{e_{2}}) \cdot \vec{\sigma}} \end{array} \label{EQ4.1.31}\]

y por lo tanto, utilizando la Ecuación 2.4.13 de la Sección 2.4.2,

\[\begin{array}{c} {\hat{e}_{1} = Tr(|\xi \rangle \langle \xi| \vec{\sigma}) = \langle \xi | \vec{\sigma} \xi \rangle} \end{array} \label{EQ4.1.32}\]

\[\begin{array}{c} {\hat{e}_{1}+ i \hat{e}_{2} = Tr(|\xi \rangle \langle \bar{\xi}| \vec{\sigma}) = \langle \bar{\xi} | \vec{\sigma} \xi \rangle} \end{array} \label{EQ4.1.33}\]

Hemos utilizado aquí la regla:

\[\begin{array}{c} {Tr(|\xi \rangle \langle \eta|) = \langle \eta | \xi \rangle} \end{array}\]

Las ecuaciones\ ref {EQ4.1.32} y\ ref {EQ4.1.33} constituyen una expresión más compacta para la relación entre una espinora y su tríada asociada. Se pueden extraer de aquí los valores de los cosenos de dirección

\[\begin{array}{cc} {\hat{e}_{j} \cdot \hat{x}_{k} \equiv e_{jk}}&{ j, k = 1, 2, 3} \end{array}\]

\[\begin{array}{c} {\hat{e}_{31} = \langle \xi | \sigma_{1} | \xi \rangle = \xi_{0} \xi_{1}^{*}+\xi_{0}^{*} \xi_{1} = \mathcal{R} (\xi_{0}^{*} \xi_{1})}\\ {\hat{e}_{32} = \langle \xi | \sigma_{2} | \xi \rangle = i(\xi_{0} \xi_{1}^{*}-\xi_{0}^{*} \xi_{1}) = \mathcal{S} (\xi_{0}^{*} \xi_{1})}\\ {\hat{e}_{33} = \langle \xi | \sigma_{3} | \xi \rangle = \xi_{0} \xi_{1}^{*}+\xi_{1}^{*} \xi_{1}} \end{array}. \label{EQ4.1.36}\]

\[\begin{array}{c} {\hat{e}_{11}+i \hat{e}_{21} = \langle \bar{\xi} | \sigma_{1} | \xi \rangle = \xi_{0}^{2}-\xi_{1}^{2}}\\ {\hat{e}_{12}+i \hat{e}_{22} = \langle \bar{\xi} | \sigma_{2} | \xi \rangle = i(\xi_{0}^{2}+\xi_{1}^{2})}\\ {\hat{e}_{13}+i \hat{e}_{23} = \langle \bar{\xi} | \sigma_{3} | \xi \rangle = -2\xi_{0} \xi_{1}} \end{array} \label{EQ4.1.37}\]

Mediante el uso de la ecuación\ ref {EQ4.1.11} obtenemos estas cantidades en términos de ángulos de Euler

\[\begin{array}{c} {e_{31} = \sin \beta \cos \alpha}\\ {e_{32} = \sin \beta \sin \alpha}\\ {e_{33} = \cos \beta} \end{array}\]

\[\begin{array}{cc} {e_{11} = \cos \gamma \cos \beta \cos \alpha- \sin \gamma \sin \alpha}&{e_{21} = -\sin \gamma \cos \beta \cos \alpha-\cos \gamma \sin \alpha}\\ {e_{12} = \cos \gamma \cos \beta \sin \alpha+\sin \gamma \cos \alpha }&{e_{22} = -\sin \gamma \cos \beta \sin \alpha+ \cos \gamma \cos \alpha }\\ {e_{13} = -\cos \gamma \sin \beta}&{e_{23} = \sin \gamma \sin \beta} \end{array}\]

La relación entre vectores y espinores mostrada en Ecuaciones\ ref {EQ4.1.36} puede establecerse también por medio de una proyección estereográfica. Este método produce resultados más rápidos que la actual larga acumulación que a su vez tiene un alcance más amplio. En lugar de rotar espacios vectoriales, operamos sobre tríadas y así obtenemos también la Ecuación\ ref {EQ4.1.37}. Que yo sepa, esta relación no ha aparecido en la literatura.

Las Ecuaciones\ ref {EQ4.1.36} y\ ref {EQ4.1.37} resuelven el problema de parametrización establecido al inicio de este capítulo. Los nueve cosenos\(e_{jk}\) de dirección interrelacionados se expresan por los tres parámetros independientes de la espinora.

Esta es la contraparte del problema de parametrización respecto a los nueve parámetros de las\(\mathcal{SO}(3)\) matrices (ver página 13), problema que ha sido resuelto por la representación SU (2) de\(\mathcal{SO}(3)\) con las matrices unitarias\(U(\hat{u}, \phi/2)\).

Es de destacar que el paso decisivo fue dado en ambos casos por Euler quien introdujo los “ángulos de Euler”\(\alpha, \beta, \gamma\) y también los parámetros eje-ángulo\(\hat{u}, \phi\) para los operadores de rotación.

Los resultados de Euler llegan a buen término en la versión de cálculo de espinas en la que las espinoras que representan estados orientacionales se parametrizan en términos de ángulos de Euler y los operadores unitarios en términos de\(\hat{u}, \phi\).

Proponemos demostrar la facilidad con que este formalismo se presta a las operaciones algebraicas. Esto se deriva particularmente de las construcciones\ ref {EQ4.1.30} y\ ref {EQ4.1.31} en las que reconocemos las matrices singulares de la Tabla 2.2 (página 46).

Definimos más a fondo

\[\begin{array}{c} {|\xi \rangle \langle \xi| = \frac{1}{2}(1+\hat{e}_{3} \cdot \vec{\sigma}) \equiv E_{3}}\\ {|\bar{\xi} \rangle \langle \bar{\xi}| = \frac{1}{2}(1-\hat{e}_{3} \cdot \vec{\sigma}) \equiv \bar{E}_{3}}\\ {|\xi \rangle \langle \bar{\xi}| = \frac{1}{2}(\hat{e}_{1}+i\hat{e}_{2}) \cdot \vec{\sigma} \equiv E_{+}}\\ {|\bar{\xi} \rangle \langle \xi| = \frac{1}{2}(\hat{e}_{1}-i\hat{e}_{2}) \cdot \vec{\sigma} \equiv E_{-} = - \bar{E}_{+}} \end{array} \label{EQ4.1.40}\]

Aquí\(E_{3}, \bar{E}_{3}\) están los operadores de proyección idempotentes y los operadores de pasos\(E_{+}, E_{-}\) nilpotentes. Desde entonces\(E_{3}+\bar{E}_{3} = 1\), tenemos

\[\begin{array}{c} {|\eta \rangle = |\xi \rangle \langle \xi | \eta \rangle+| \bar{\xi} \rangle \langle \bar{\xi} | \eta \rangle} \end{array}\]

\[\begin{array}{c} {= |\xi \rangle a_{0}+|\bar{\xi} \rangle a_{1}} \end{array} \label{EQ4.1.42}\]

con

\[\begin{array}{cc} {a_{0} = \langle \xi | \eta \rangle}&{a_{1} = \langle \bar{\xi} | \eta \rangle} \end{array} \label{EQ4.1.43}\]

También,

\[\begin{array}{cc} {E_{+} | \bar{\xi} \rangle = | \xi \rangle}&{ E_{-}| \xi \rangle = | \bar{\xi} \rangle} \end{array}\]

\[\begin{array}{cc} {E_{+} | \xi \rangle = 0}&{ E | \bar{\xi} \rangle = 0} \end{array}\]

Vemos de Ecuaciones\ ref {EQ4.1.40} que la transición\(|\xi \rangle \rightarrow | \bar{\xi} \rangle\) corresponde a una inversión del eje de la figura con una inversión simultánea de la\(\gamma\) -rotación alrededor del eje. Por lo tanto, la transformación corresponde a una transición de un marco derecho a uno izquierdo con un cambio simultáneo de antihorario a horario como sentido positivo de rotación. Por lo tanto, debemos mirar la transición de 4.1.40c a 4.1.40d como\(E_{+} \rightarrow \bar{E}_{+}\), o

\[\begin{array}{c} {\frac{1}{2} (\hat{e}_{1}+i \hat{e}_{2}) \cdot \vec{\sigma} \rightarrow 1[-\hat{e}_{1}-i(-\hat{e}_{2})] \cdot \vec{\sigma}} \end{array}\]

Todo esto es evidente también si representamos la transición\(|\xi \rangle \rightarrow | \bar{\xi} \rangle\) en términos de ángulos de Euler como

\[\begin{array}{c} {\alpha \rightarrow \pi+\alpha} \end{array}\]

\[\begin{array}{c} {\beta \rightarrow \pi-\beta} \end{array}\]

\[\begin{array}{c} {\gamma \rightarrow \pi-\gamma} \end{array}\]

Tomamos nota también de las siguientes relaciones para su uso posterior:

\[\begin{array}{cc} {E_{-}E_{+} = \bar{E}_{3}}&{E_{+}E_{-} = E_{3}} \end{array}\]

Además de los símbolos cortos\(|\xi \rangle, | \bar{\xi} \rangle\) para las espinoras y sus conjugados, utilizaremos también notaciones más explícitas dependiendo del contexto:

\[\begin{array}{c} {|\alpha, \beta, \gamma \rangle = |\pi+\alpha, \pi-\beta, \pi-\gamma \rangle} \end{array}\]

\[\begin{array}{c} {|\hat{k} \gamma \rangle, |\hat{k} \gamma \rangle = |-\hat{k}, \pi-\gamma \rangle} \end{array}\]

\[\begin{array}{c} {|\hat{k} \rangle, |\hat{k} \rangle = |-\hat{k} \rangle} \end{array}\]

Aquí\(\hat{k}\) está el vector unitario denotado por\(\hat{e}_{3}\), en la Ecuación 5.1.30. Su asociación con la espinora es evidente a partir del siguiente problema de valores propios.

Mediante el uso de Ecuaciones\ ref {EQ4.1.40} y\ ref {EQ4.1.18} obtenemos

\[\begin{array}{c} {\frac{1}{2}(1+\hat{k} \cdot \vec{\sigma}) | \hat{k} \rangle = | \hat{k} \rangle \langle \hat{k} | \hat{k} \rangle = | \hat{k} \rangle} \end{array}\]

\[\begin{array}{c} {\frac{1}{2}(1-\hat{k} \cdot \vec{\sigma}) | \bar{\hat{k}} \rangle = | \bar{\hat{k}} \rangle \langle \bar{\hat{k}} | \bar{\hat{k}} \rangle = | \bar{\hat{k}} \rangle} \end{array}\]

De ahí

\[\begin{array}{c} {\hat{k} \cdot \vec{\sigma} | \hat{\rangle} k = | \hat{k} \rangle} \end{array} \label{EQ4.1.56}\]

\[\begin{array}{c} {\hat{k} \cdot \vec{\sigma} | \hat{\rangle} k = | \hat{k} \rangle} \end{array} \label{EQ4.1.57}\]

Así\(| k \rangle\) y\(| \hat{k} \rangle\) son vectores propios del operador hermitiano\(k \cdot \vec{\sigma}\), con los valores propios\(+1\) y\(-1\) respectivamente. Este es un resultado bien conocido, aunque generalmente se obtiene por un cómputo algo más largo.

Mediante el uso de la expresión explícita para\(U (\hat{k}, \phi/2)\) obtenemos de\ ref {EQ4.1.56} y\ ref {EQ4.1.57}

\[\begin{array}{c} {U(\hat{k}, \phi/2) | \hat{k}, \gamma \rangle = \exp (-i \phi/2) | \hat{k}, \gamma \rangle = | \hat{k}, \gamma+ \phi \rangle} \end{array}\]

\[\begin{array}{c} {U(\hat{k}, \phi/2) | \overline{\hat{k}, \gamma} \rangle = \exp (i \phi/2) | \overline{\hat{k}, \gamma} \rangle = | \overline{\hat{k}, \gamma+ \phi} \rangle} \end{array}\]

También está la matriz diagonal unitaria

\[\begin{array}{c} {U(\hat{x}_{3}, \phi/2) = \begin{pmatrix} {e^{-i \phi/2}}&{0}\\ {0}&{e^{-i \phi/2}} \end{pmatrix}} \end{array}\]

cuyo efecto se describe fácilmente:

\[\begin{array}{c} {U(\hat{x}_{3}, \phi/2) |\alpha, \beta, \gamma \rangle = |\alpha+\phi, \beta, \gamma \rangle} \end{array}\]

Estas relaciones sacan a relucir el carácter “biaxial” de los espinores: ambos\(\hat{x}_{3}\), y\(\hat{k}\) juegan un papel distinguido. Lo mismo ocurre con una matriz unitaria parametrizada en términos de ángulos de Euler:\(V (\alpha, \beta, \gamma)\) o parámetros de Cayley-Klein. Esto se va a contrastar con la forma uniaxial\(U(\hat{u}, \phi/2)\).

Nuestra discusión en este capítulo ha sido hasta ahora puramente geométrica aunque se puede dar una interpretación cinemática a las transformaciones activas de objetos geométricos. Ahora vamos un paso más allá e introducimos el concepto de tiempo. Al establecer\(\phi = \omega t\) con una constante\(\omega\) en el operador de rotación unitaria obtenemos la descripción de los procesos de rotación:

\[\begin{array}{c} {U(\hat{k}, \frac{\omega t}{2}) | \hat{k}, \frac{\gamma}{2} \rangle = \exp (-i \omega t/2) | \hat{k}, \frac{\gamma}{2} \rangle = | \hat{k}, \frac{\gamma+ \omega t}{2} \rangle}\\ {U(\hat{k}, \frac{\omega t}{2}) | \overline{\hat{k}, \frac{\gamma}{2}} \rangle = \exp (-i \omega t/2) | \hat{k}, \frac{\gamma}{2} \rangle = | \overline{\hat{k}, \frac{\gamma+ \omega t}{2}} \rangle} \end{array} \label{EQ4.1.62}\]

Estas rotaciones son estacionarias, porque U opera sobre sus propios hiladores. También hay varias formas de representar la evolución de los espinores arbitrarios. Tenemos

\[\begin{array}{c} {U(\hat{k}, \frac{\omega t}{2}) | \eta \rangle = \exp (-i \frac{\omega t}{2} \hat{k} \cdot \vec{\sigma}) | \eta \rangle}\\ {\langle \eta | U^{-1}(\hat{k}, \frac{\omega t}{2}) = \langle \eta | \exp (i \frac{\omega t}{2} \hat{k} \cdot \vec{\sigma})} \end{array} \label{EQ4.1.63}\]

O, en forma diferencial

\[\begin{array}{c} {i | \dot{\eta} \rangle = \frac{\omega}{2} \hat{k} \cdot \vec{\sigma} | \eta \rangle}\\ {-i \langle \dot{\eta} | = \langle \eta | \frac{\omega}{2} \hat{k} \cdot \vec{\sigma}} \end{array} \label{EQ4.1.64}\]

Las funciones de estado que resuelven estas ecuaciones diferenciales se obtienen explícitamente usando Ecuaciones\ ref {EQ4.1.42},\ ref {EQ4.1.43},\ ref {EQ4.1.62} y\ ref {EQ4.1.63}:

\[\begin{array}{c} {| \eta(t) \rangle = U(\hat{k}, \frac{\omega t}{2}) | \eta (0) \rangle = \exp (-i \omega t/2) | \hat{k} \rangle a_{0} + \exp (i \omega t/2) | \bar{\hat{k}} \rangle a_{1}} \end{array}\]

y de manera similar para\(\langle \eta(t) |\).

Al introducir el símbolo H para el operador hermitiano\(H = (\omega t/2) \hat{k} \cdot \vec{\sigma}\) en\ ref {EQ4.1.64} obtenemos

\[\begin{array}{c} {i | \dot{\eta} \rangle = H | \eta \rangle} \end{array}\]

\[\begin{array}{c} {-i \langle \dot{\eta} | = \langle \eta | H} \end{array}\]

Estas ecuaciones recuerdan a la ecuación de Schro ̈dinger. También sería fácil derivar de aquí una ecuación de operador tipo Heisenberg.

Debe ser evidente para quienes están familiarizados con la mecánica cuántica, que todo nuestro formalismo espinor tiene un sabor mecánico marcadamente cuántico. Lo que todo esto significa es que la orientabilidad de los objetos es de primordial importancia en la mecánica cuántica y el concepto de la tríada nos proporciona un camino más directo hacia la cuantificación, o a algunos aspectos de la misma, que el enfoque tradicional de masa puntual.

Para aprovechar esta oportunidad, tenemos que aplicar nuestro formalismo espinor a los sistemas físicos.

Nuestro uso del concepto de tiempo en las Ecuaciones 4.1.62—4.1.66 es bastante formal. Solo seleccionamos un subgrupo de un parámetro del grupo de rotación para describir posibles tipos de rotación estacionaria.

Tenemos que recurrir a la experimentación, o a una teoría dinámica experimentalmente establecida, para decidir si tales movimientos ocurren realmente en la naturaleza. Examinaremos esta cuestión en relación con la rotación del cuerpo rígido en la siguiente sección.

Sin embargo, nuestro principal objetivo es la discusión de la luz polarizada. Aquí la conexión entre las teorías clásica y cuántica es muy estrecha y el procedimiento de cuantificación es particularmente claro en términos del formalismo espinor.

El hecho de que el mismo formalismo pueda ajustarse tanto al movimiento rígido del cuerpo como a una onda phe nomenon es interesante por sí mismo. Sabemos que la dualidad partícula-onda se encuentra entre los temas centrales de la mecánica cuántica. El contraste entre estos objetos es muy pronunciado si nos afinamos a nosotros mismos para apuntar partículas y a ondas escalares. Es notable cómo se atenúa este contraste en el contexto de problemas rotacionales.

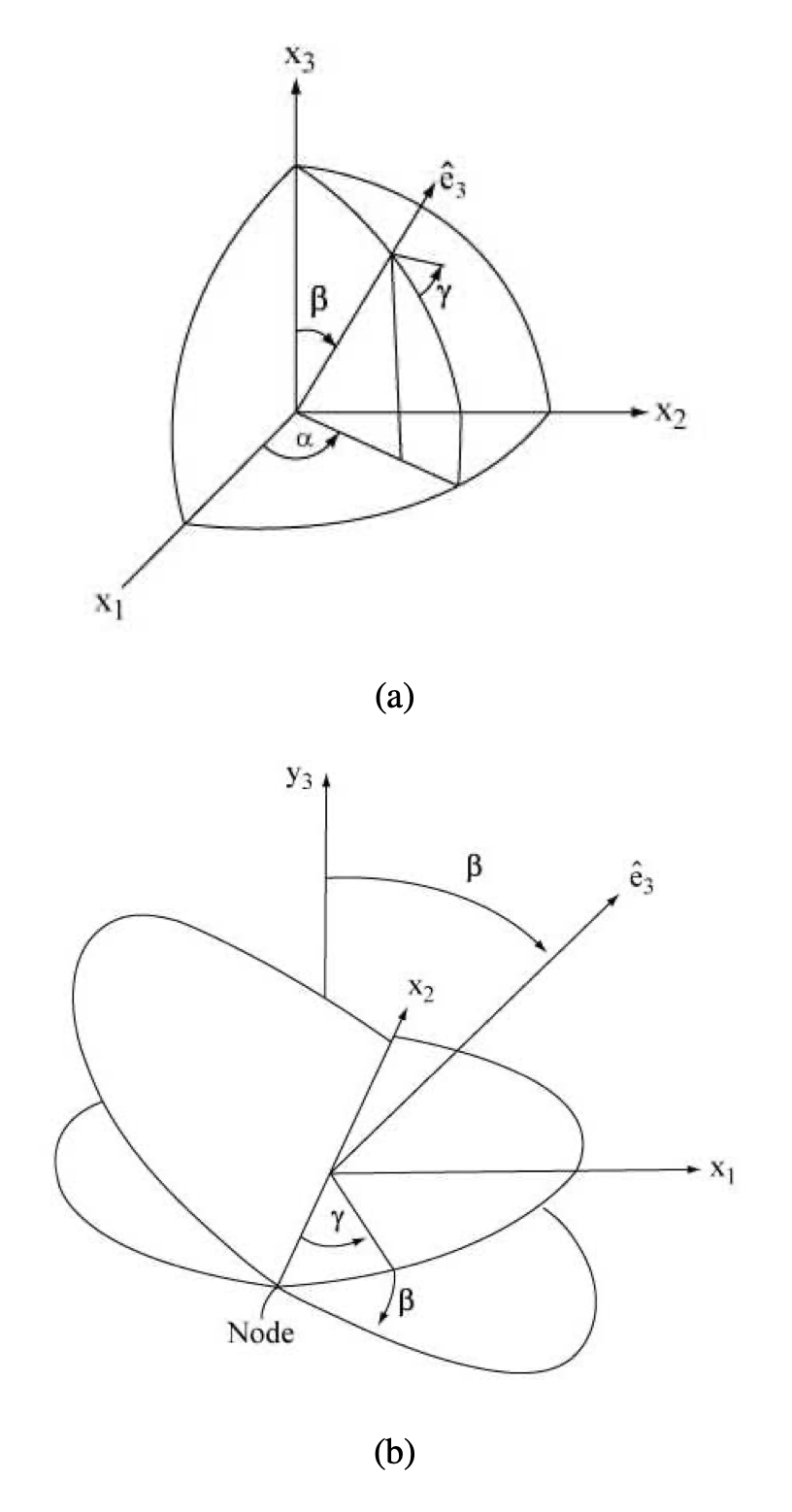
Figura 4.1: Ángulos de Euler: (a) Imagen estática. (b) Visualización Cinemática.