4.5: Revisión de SU (2) y vista previa de la cuantificación

Nuestra introducción del concepto espinor al inicio de la Sección 4.1 puede racionalizarse sobre la base de las siguientes pautas. Primero, requerimos una cierta economía y deseamos evitar tratar con parámetros redundantes al especificar una tríada giratoria, tal como hemos resuelto previamente el problema análogo para el operador de rotación.

Segundo, deseamos tener un formalismo eficiente para representar el problema rotacional.

Hemos visto que las matrices de\(\mathcal{SU}(2)\) satisfacer todos estos requisitos, pero nos encontramos ensillados con una dos-valorización de la representación:\(| \xi \rangle\) y\(| \xi \rangle\) corresponden a la misma configuración de tríada. Esto no es un problema grave, ya que nuestras relaciones clave 4.1.36 y 4.1.37 son cuadráticas en\(| \xi \rangle\).

De esta manera, el doble valor appera aquí solo como una ayuda computacional que desaparece en el resultado final.

La situación es diferente si nos fijamos en las fórmulas 4.1.42—4.1.66 de la misma sección (Sección 4.1). Estas ecuaciones son lineales, tienen un carácter mecánico cuántico y sabemos que efectivamente son aplicables en el contexto adecuado. Es un hecho pragmático el dos-valor no es sólo una molestia necesaria, sino que tiene un significado físico. Pero entender este significado es un reto que solo podemos enfrentar en pasos cuidadosamente elegidos.

Deseamos dar una interpretación más física a la tríada, pero evitar el estancamiento del cuerpo rígido. Primero asociamos el espacio abstracto de Poincaré con el sistema físico del oscilador degenerado bidimensional. La rotación en el espacio Poincaré se asocia con un desplazamiento de fase entre estados conjugados, que se traduce en una rotación de la esfera de Poincaré, interpretada a su vez como un cambio de orientación, o cambio de forma de los patrones vibratorios en el espacio ordinario.

Es sólo una leve exageración decir que nuestra transición de la tríada en el espacio euclidiano al espacio de Poincaré es algo así como una “cuantificación”, en el sentido de que la ecuación de onda de Schro ̈dinger asocia una onda con una partícula. (¡La h de Planck es entrar en breve!)

En esta teoría tenemos un buen uso para las espinoras conjugadas\(| \xi \rangle\) y\(| \bar{\xi} \rangle\) que representan polarizaciones opuestas, pero debemos identificarnos\(| \bar{\bar{\xi}} \rangle = -| \xi \rangle\) con\(| \xi \rangle\).

Lo anterior no es más que un modelo cinemático perfectamente definido. El siguiente paso es diferente. Como “segunda cuantificación” introducimos la h de Planck para definir fotones individuales. Una división de haz representada por un operador de proyección se puede expresar en términos probabilísticos.

Formalmente todo esto es fácil y tendríamos de inmediato una gran parte del formalismo mecánico cuántico que involucra la teoría de la medición.

A continuación, podríamos tomarnos en serio el doble valor del espinor y obtener el formalismo de la isospin y del neutrino, digamos como en la Sección 17, Estados Fermion, en [Kae65].

Por último, en lugar de vibraciones doblemente degeneradas, podríamos considerar el vibrador triplicamente degenerado y manejarlo por\(\mathcal{SU}(3)\) [Lip02]. No consideraremos estas generalizaciones en este punto, sin embargo. Antes de ampliar aún más el formalismo debemos esperar entender mejor lo que ya tenemos.

En primer lugar, una observación formal. Nuestros resultados desarrollados hasta ahora están determinados de manera única por el formalismo espinor de la Sección 4.1 y por el programa de considerar la esfera de Poincaré como el espacio de configuración básica a describir por coordenadas esféricas convencionales\(\alpha, \beta\) o\(\phi, \theta\).

Es de destacar que este modesto equipo conceptual nos lleva hasta el momento. Hemos obtenido espinores, matrices de densidad y hemos discutido al menos fugaz coherencia, incoherencia, teoría cuántica de medición y teoría de transformación.

Lo que no sacamos de la teoría es una interpretación específica del proceso vibratorio subyacente ya que el formalismo es hasta ahora totalmente independiente del mismo. Este hecho nos da algo por debajo del alcance y límite de la mecánica cuántica. Podemos aplicar el formalismo a fenómenos que entendemos muy poco. Sin embargo, dado que el mismo\(\mathcal{SU}(2)\) formalismo se aplica a la luz polarizada, espín, isospin, extrañeza y otros fenómenos, aprendemos poco sobre sus aspectos distintivos.

Para superar esta limitación necesitamos una comprensión más profunda de lo que es un momento angular cuantificado en el marco de un problema dinámico.

El siguiente capítulo está dedicado a una discusión fenomenológica de los conceptos de partícula y onda. Intentaremos obtener suficientes pistas para desarrollar una teoría dinámica en forma de geometría de espacio de fase en el Capítulo VI.

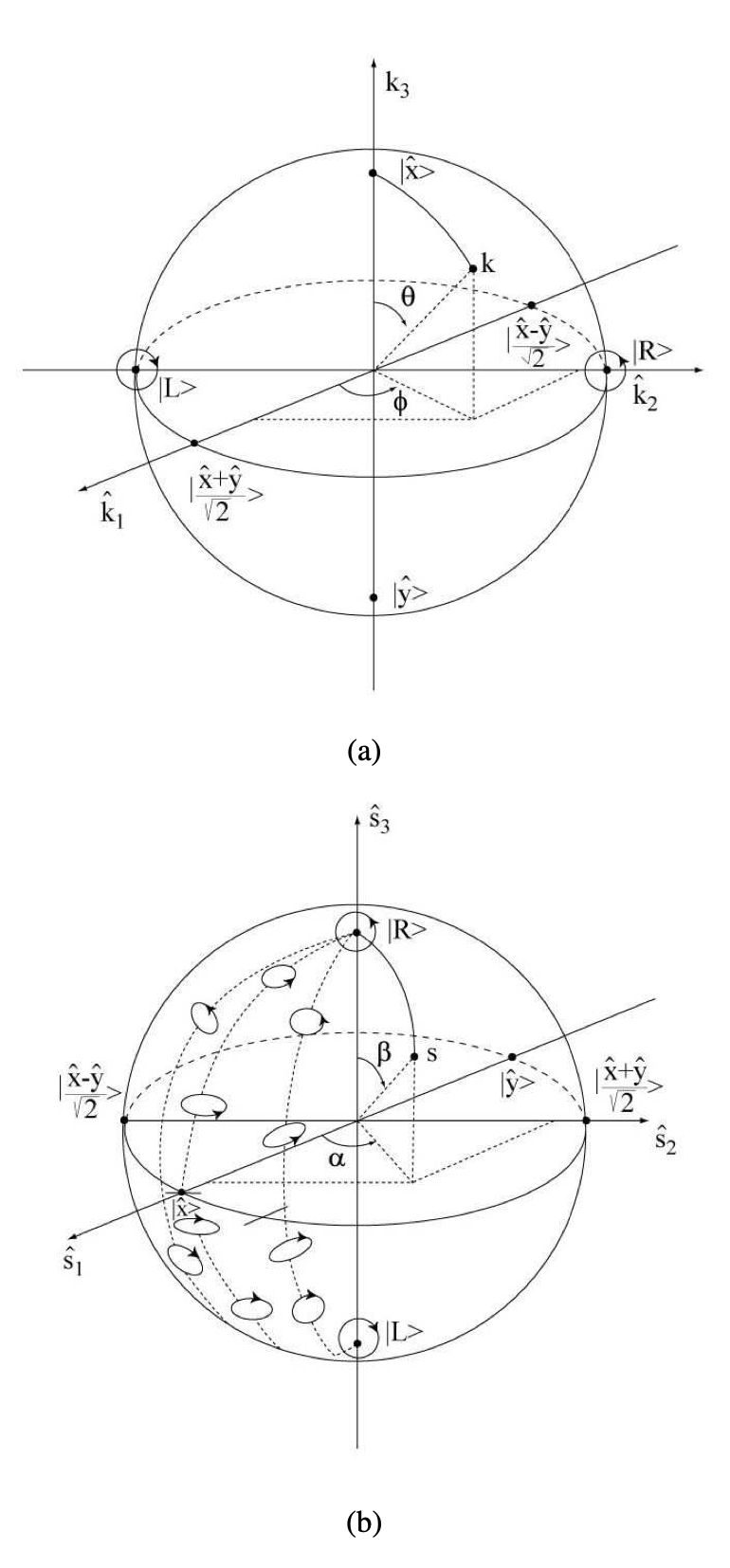
Figura 4.3: Representación de la polarización en la esfera de Poincaré. Conexión entre los esquemas: a)\(\hat{k} (\phi, \theta)\) esquema y b)\(\hat{s} (\alpha, \beta)\) esquema.

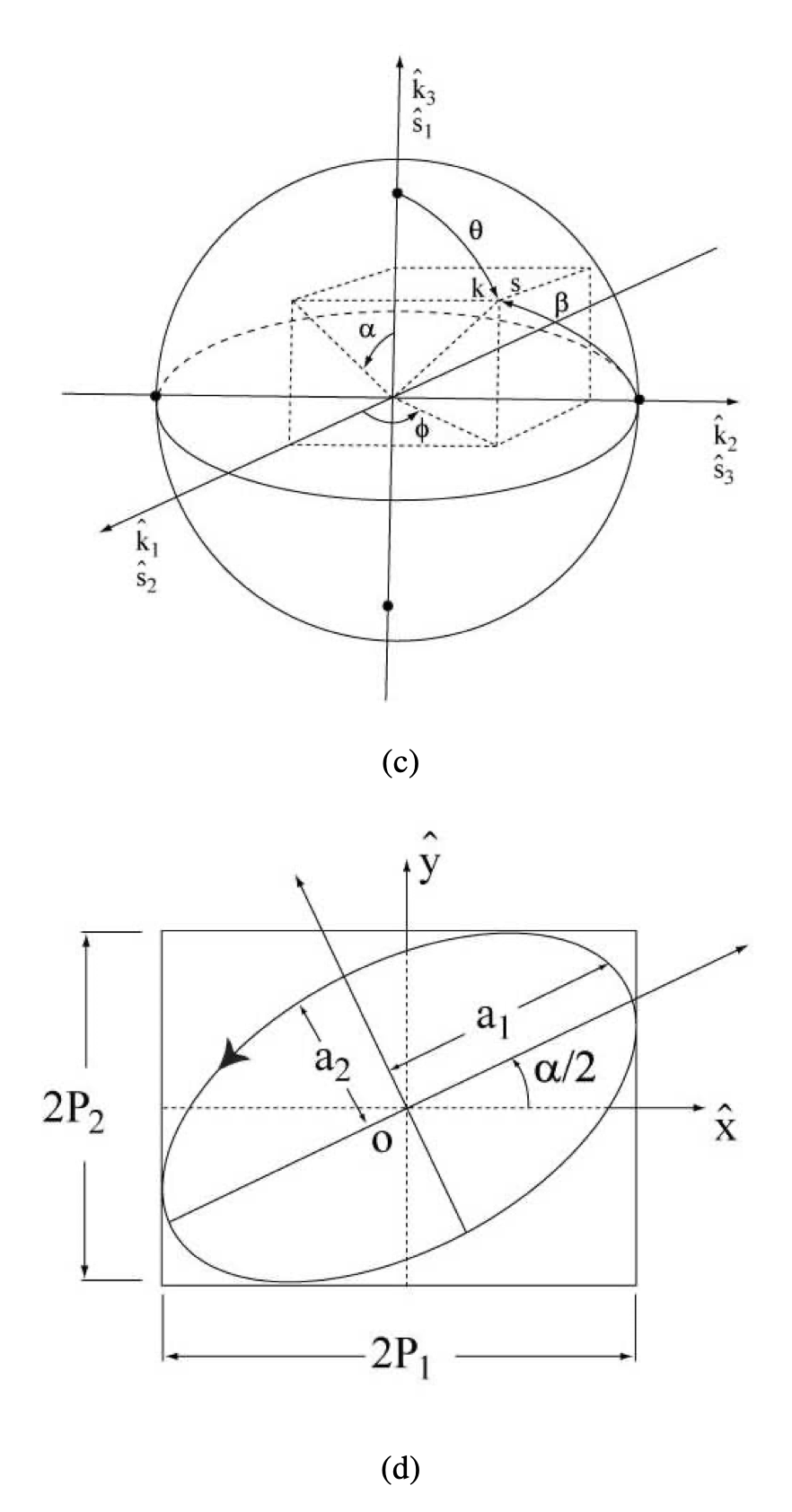
Figura 4.4: Representación de la polarización en la esfera de Poincaré. Conexión entre los esquemas (c) y (d).