1.2: Conjuntos y Relaciones de Equivalencia

Teoría de Conjuntos

Un conjunto es una colección bien definida de objetos; es decir, se define de tal manera que podemos determinar para cualquier objeto dado\(x\) si\(x\) pertenece o no al conjunto. Los objetos que pertenecen a un conjunto se denominan sus elementos o miembros. Denotaremos conjuntos por letras mayúsculas, como\(A\) o\(X\text{;}\) si\(a\) es un elemento del conjunto\(A\text{,}\) que escribimos\(a \in A\text{.}\)

Un conjunto generalmente se especifica listando todos sus elementos dentro de un par de llaves o indicando la propiedad que determina si un objeto\(x\) pertenece o no al conjunto. Podríamos escribir

\[ X = \{ x_1, x_2, \ldots, x_n \} \nonumber \]

para un conjunto que contenga elementos\(x_1, x_2, \ldots, x_n\) o

\[ X = \{ x :x \text{ satisfies }{\mathcal P}\} \nonumber \]

si cada uno\(x\) en\(X\) satisface una determinada propiedad\({\mathcal P}\text{.}\) Por ejemplo, si\(E\) es el conjunto de enteros positivos pares, podemos describir\(E\) escribiendo ya sea

\[ E = \{2, 4, 6, \ldots \} \quad \text{or} \quad E = \{ x : x \text{ is an even integer and } x \gt 0 \}\text{.} \nonumber \]

Escribimos\(2 \in E\) cuando queremos decir que 2 está en el set\(E\text{,}\) y\(-3 \notin E\) decir que no\(-3\) está en el conjunto\(E\text{.}\)

Algunos de los conjuntos más importantes que consideraremos son los siguientes:

\ begin {reunir*} {\ mathbb N} =\ {n: n\ text {es un número natural}\} =\ {1, 2, 3,\ ldots\};\\ {\ mathbb Z} =\ {n: n\ text {es un entero}\} =\ {\ ldots, -1, 0, 1, 2,\ ldots\};\\ {\ mathbb Q} =\ {r: r\ text {es un número racional}\} =\ {p/q: p, q\ in {\ mathbb Z}\ text {donde} q\ neq 0\};\\ {\ mathbb R} =\ {x: x \ text {es un número real}\};\\ {\ mathbb C} =\ {z: z\ text {es un número complejo}\}\ text {.} \ end {reunir*}

Podemos encontrar diversas relaciones entre conjuntos así como realizar operaciones en conjuntos. Un conjunto\(A\) es un subconjunto de\(B\text{,}\) escritos\(A \subset B\) o\(B \supset A\text{,}\) si cada elemento de\(A\) es también un elemento de\(B\text{.}\) Por ejemplo,

\[ \{4,5,8\} \subset \{2, 3, 4, 5, 6, 7, 8, 9 \} \nonumber \]

y

\[ {\mathbb N} \subset {\mathbb Z} \subset {\mathbb Q} \subset {\mathbb R} \subset {\mathbb C}\text{.} \nonumber \]

Trivialmente, cada conjunto es un subconjunto de sí mismo. Un conjunto\(B\) es un subconjunto propio de un conjunto\(A\) si\(B \subset A\) pero\(B \neq A\text{.}\) si no\(A\) es un subconjunto de\(B\text{,}\) escribimos\(A \not \subset B\text{;}\) por ejemplo,\(\{4, 7, 9\} \not \subset \{2, 4, 5, 8, 9 \}\text{.}\) Dos conjuntos son iguales, escritos\(A = B\text{,}\) si podemos mostrar que\(A \subset B\) y\(B \subset A\text{.}\)

Es conveniente tener un conjunto sin elementos en él. Este conjunto se llama el conjunto vacío y se denota por\(\emptyset\text{.}\) Note que el conjunto vacío es un subconjunto de cada conjunto.

Para construir nuevos conjuntos a partir de conjuntos antiguos, podemos realizar ciertas operaciones: la unión\(A \cup B\) de dos conjuntos\(A\) y\(B\) se define como

\[ A \cup B = \{x : x \in A \text{ or } x \in B \}; \nonumber \]

la intersección de\(A\) y\(B\) está definida por

\[ A \cap B = \{x : x \in A \text{ and } x \in B \}\text{.} \nonumber \]

Si\(A = \{1, 3, 5\}\) y\(B = \{ 1, 2, 3, 9 \}\text{,}\) entonces

\[ A \cup B = \{1, 2, 3, 5, 9 \} \quad \text{and} \quad A \cap B = \{ 1, 3 \}\text{.} \nonumber \]

Podemos considerar la unión y la intersección de más de dos conjuntos. En este caso escribimos

\[ \bigcup_{i = 1}^{n} A_{i} = A_{1} \cup \ldots \cup A_n \nonumber \]

y

\[ \bigcap_{i = 1}^{n} A_{i} = A_{1} \cap \ldots \cap A_n \nonumber \]

para la unión e intersección, respectivamente, de los conjuntos\(A_1, \ldots, A_n\text{.}\)

Cuando dos conjuntos no tienen elementos en común, se dice que son disjuntos; por ejemplo, si\(E\) es el conjunto de enteros pares y\(O\) es el conjunto de enteros impares, entonces\(E\) y\(O\) son disjuntos. Dos juegos\(A\) y\(B\) están disjuntas exactamente cuando\(A \cap B = \emptyset\text{.}\)

A veces trabajaremos dentro de un conjunto fijo\(U\text{,}\) llamado el conjunto universal. Para cualquier conjunto\(A \subset U\text{,}\) definimos el complemento de\(A\text{,}\) denotado por\(A'\text{,}\) ser el conjunto

\[ A' = \{ x : x \in U \text{ and } x \notin A \}\text{.} \nonumber \]

Definimos la diferencia de dos conjuntos\(A\) y\(B\) ser

\[ A \setminus B = A \cap B' = \{ x : x \in A \text{ and } x \notin B \}\text{.} \nonumber \]

Ejemplo\(1.1\)

\({\mathbb R}\)Sea el conjunto universal y supongamos que

\[ A = \{ x \in {\mathbb R} : 0 \lt x \leq 3 \} \quad \text{and} \quad B = \{ x \in {\mathbb R} : 2 \leq x \lt 4 \}\text{.} \nonumber \]

Solución

Entonces

\ begin {alinear*} A\ cap B & =\ {x\ in {\ mathbb R}: 2\ leq x\ leq 3\}\\ A\ copa B & =\ {x\ in {\ mathbb R}: 0\ lt x\ lt 4\}\ A\ setmenos B & =\ {x\ in {\ mathbb R}: 0\ lt x\ lt 2\}\\ A' & =\ {x\ in {\ mathbb R}: x\ leq 0\ texto {o} x\ gt 3\}\ texto {.} \ end {alinear*}

Proposición\(1.2\)

Dejar\(A\text{,}\)\(B\text{,}\) y\(C\) ser conjuntos. Entonces

1. \(A \cup A = A\text{,}\)\(A \cap A = A\text{,}\)y\(A \setminus A = \emptyset\text{;}\)
2. \(A \cup \emptyset = A\)y\(A \cap \emptyset = \emptyset\text{;}\)
3. \(A \cup (B \cup C) = (A \cup B) \cup C\)y\(A \cap (B \cap C) = (A \cap B) \cap C\text{;}\)
4. \(A \cup B = B \cup A\)y\(A \cap B = B \cap A\text{;}\)
5. \(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\text{;}\)
6. \(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\text{.}\)

Prueba

Demostraremos (1) y (3) y dejaremos que se prueben los resultados restantes en los ejercicios.

(1) Observar que

\ begin {alinear*} A\ copa A & =\ {x: x\ en A\ texto {o} x\ en A\}\\ & =\ {x: x\ en A\}\\ & = A\ end {alinear*}

y

\ begin {alinear*} A\ cap A & =\ {x: x\ en A\ texto {y} x\ en A\}\\ & =\ {x: x\ en A\}\\ & = A\ texto {.} \ end {alinear*}

También,\(A \setminus A = A \cap A' = \emptyset\text{.}\)

(3) Para juegos\(A\text{,}\)\(B\text{,}\) y\(C\text{,}\)

\ begin {alinear*} A\ copa (B\ copa C) & = A\ copa\ {x: x\ en B\ texto {o} x\ en C\}\\ & =\ {x: x\ en A\ texto {o} x\ en B,\ texto {o} x\ en C\}\\ & =\ {x: x\ en A\ texto {o} x\ en B\}\ copa C\\ & = (A\ copa B)\ copa C\ texto {.} \ end {alinear*}

Un argumento similar demuestra que\(A \cap (B \cap C) = (A \cap B) \cap C\text{.}\)

Teorema\(1.3\). De Morgan's Laws

Dejar\(A\) y\(B\) ser conjuntos. Entonces

1. \((A \cup B)' = A' \cap B'\text{;}\)
2. \((A \cap B)' = A' \cup B'\text{.}\)

Prueba

(1) Si\(A \cup B = \emptyset\text{,}\) entonces el teorema sigue inmediatamente ya que ambos\(A\) y\(B\) son el conjunto vacío. De lo contrario, debemos demostrar eso\((A \cup B)' \subset A' \cap B'\) y\((A \cup B)' \supset A' \cap B'\text{.}\) Let\(x \in (A \cup B)'\text{.}\)\(x \notin A \cup B\text{.}\) Entonces Así no\(x\) está\(A\) ni dentro ni en\(B\text{,}\) por la definición de la unión de conjuntos. Por la definición del complemento,\(x \in A'\) y\(x \in B'\text{.}\) Por lo tanto,\(x \in A' \cap B'\) y tenemos\((A \cup B)' \subset A' \cap B'\text{.}\)

Para mostrar la inclusión inversa, supongamos que\(x \in A' \cap B'\text{.}\) Entonces\(x \in A'\) y tal\(x \in B'\text{,}\) y Así\(x \notin A\) y así\(x \notin B\text{.}\) Por lo\(x \in (A \cup B)'\text{.}\) tanto,\(x \notin A \cup B\) y así,\((A \cup B)' \supset A' \cap B'\) y así\((A \cup B)' = A' \cap B'\text{.}\)

La prueba de (2) se deja como ejercicio.

Ejemplo\(1.4\)

Otras relaciones entre conjuntos suelen ser ciertas. Por ejemplo,

\[ ( A \setminus B) \cap (B \setminus A) = \emptyset\text{.} \nonumber \]

Solución

Para ver que esto es cierto, observe que

\ begin {align*} (A\ setmenos B)\ cap (B\ setmenos A) & = (A\ cap B')\ cap (B\ cap A')\\ & = A\ cap A'\ cap B\ cap B'\ & =\ emptyset\ text {.} \ end {alinear*}

Productos Cartesianos y Mapeos

Dados conjuntos\(A\) y\(B\text{,}\) podemos definir un nuevo conjunto\(A \times B\text{,}\) llamado el producto cartesiano de\(A\) y\(B\text{,}\) como un conjunto de pares ordenados. Es decir,

\[ A \times B = \{ (a,b) : a \in A \text{ and } b \in B \}\text{.} \nonumber \]

Ejemplo\(1.5\)

Si\(A = \{ x, y \}\text{,}\)\(B = \{ 1, 2, 3 \}\text{,}\) y\(C = \emptyset\text{,}\)

Solución

entonces\(A \times B\) es el conjunto

\[ \{ (x, 1), (x, 2), (x, 3), (y, 1), (y, 2), (y, 3) \} \nonumber \]

y

\[ A \times C = \emptyset\text{.} \nonumber \]

Definimos el producto cartesiano de\(n\) conjuntos para ser

\[ A_1 \times \cdots \times A_n = \{ (a_1, \ldots, a_n): a_i \in A_i \text{ for } i = 1, \ldots, n \}\text{.} \nonumber \]

Si\(A = A_1 = A_2 = \cdots = A_n\text{,}\) escribimos a menudo\(A^n\) para\(A \times \cdots \times A\) (donde se\(A\) escribirían\(n\) tiempos). Por ejemplo, el conjunto\({\mathbb R}^3\) consiste en todas las 3-tuplas de números reales.

Los subconjuntos de\(A \times B\) se llaman relaciones. Vamos a definir un mapeo o función\(f \subset A \times B\) de un conjunto\(A\) a un conjunto\(B\) para que sea el tipo especial de relación donde cada elemento\(a \in A\) tiene un elemento único\(b \in B\) tal que\((a, b) \in f\text{.}\) Otra forma de decir esto es que para cada elemento en\(A\text{,}\)\(f\) asigna un elemento único en\(B\text{.}\) Normalmente escribimos\(f:A \rightarrow B\) o\(A \stackrel{f}{\rightarrow} B\text{.}\) En lugar de escribir pares ordenados\((a,b) \in A \times B\text{,}\) escribimos\(f(a) = b\) o\(f : a \mapsto b\text{.}\) El conjunto\(A\) se llama el dominio de\(f\) y

\[ f(A) = \{ f(a) : a \in A \} \subset B \nonumber \]

se llama el rango o imagen de\(f\text{.}\) Podemos pensar en los elementos en el dominio de la función como valores de entrada y los elementos en el rango de la función como valores de salida.

Ejemplo\(1.6\)

Supongamos\(A = \{1, 2, 3 \}\) y\(B = \{a, b, c \}\text{.}\)

Solución

En la Figura 1.7 definimos relaciones\(f\) y\(g\) de\(A\) a\(B\text{.}\) La relación\(f\) es un mapeo, pero no\(g\)\(1 \in A\) es porque no esté asignado a un elemento único en\(B\text{;}\) eso es,\(g(1) = a\) y\(g(1) = b\text{.}\)

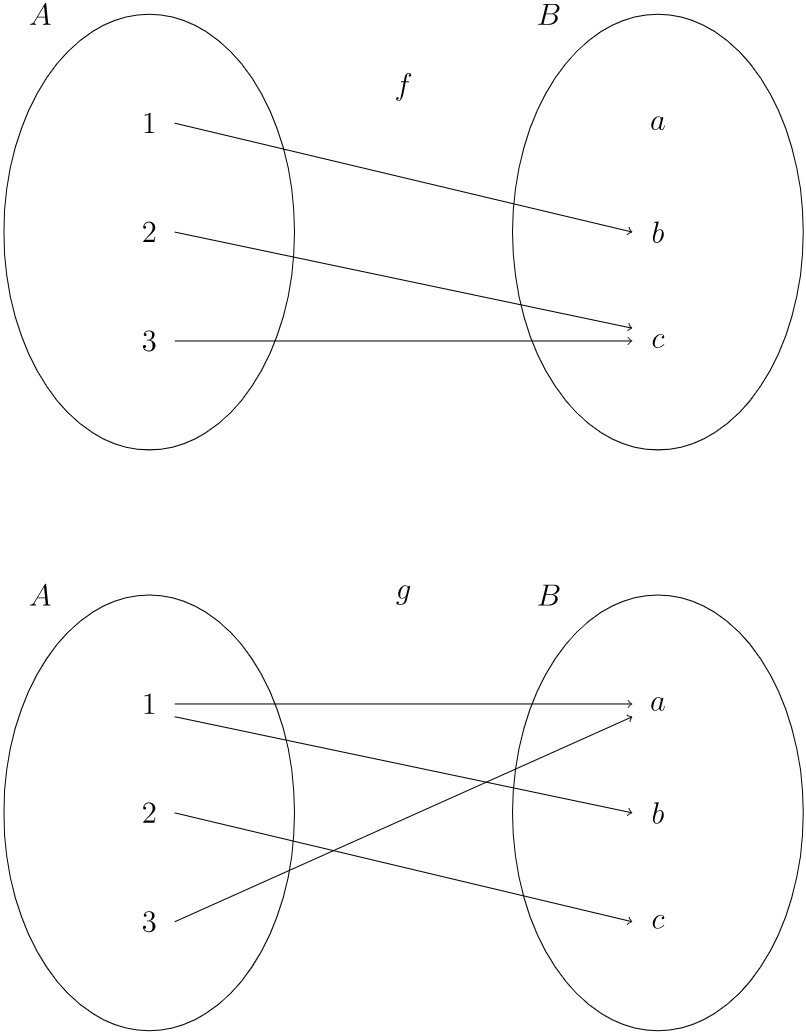
\(Figure \text { } 1.7\). Mapeos y relaciones

Dada una función a menudo\(f : A \rightarrow B\text{,}\) es posible escribir una lista describiendo lo que la función hace a cada elemento específico del dominio. Sin embargo, no todas las funciones pueden describirse de esta manera. Por ejemplo, la función\(f: {\mathbb R} \rightarrow {\mathbb R}\) que envía cada número real a su cubo es un mapeo que debe describirse escribiendo\(f(x) = x^3\) o\(f:x \mapsto x^3\text{.}\)

Considera la relación que nos\(f : {\mathbb Q} \rightarrow {\mathbb Z}\) da\(f(p/q) = p\text{.}\) Sabemos que\(1/2 = 2/4\text{,}\) pero es\(f(1/2) = 1\) o\(2\text{?}\) Esta relación no puede ser un mapeo porque no está bien definida. Una relación está bien definida si cada elemento del dominio se asigna a un elemento único en el rango.

Si\(f:A \rightarrow B\) es un mapa y la imagen de\(f\) es\(B\text{,}\) i.e.,\(f(A) = B\text{,}\) entonces\(f\) se dice que es sobre o suryectiva. En otras palabras, si existe un\(a \in A\) para cada uno de\(b \in B\) tales que\(f(a) = b\text{,}\) entonces\(f\) está sobre. Un mapa es uno a uno o inyectivo si\(a_1 \neq a_2\) implica\(f(a_1) \neq f(a_2)\text{.}\) Equivalentemente, una función es uno a uno si\(f(a_1) = f(a_2)\) implica\(a_1 = a_2\text{.}\) Un mapa que es tanto uno a uno como sobre se llama biyectiva.

Ejemplo\(1.8\)

Dejar\(f:{\mathbb Z} \rightarrow {\mathbb Q}\) ser definido por\(f(n) = n/1\text{.}\)

Solución

Entonces\(f\) es uno a uno pero no sobre. Definir\(g : {\mathbb Q} \rightarrow {\mathbb Z}\) por\(g(p/q) = p\) donde\(p/q\) es un número racional expresado en sus términos más bajos con un denominador positivo. La función\(g\) es sobre pero no uno a uno.

Dadas dos funciones, podemos construir una nueva función usando el rango de la primera función como dominio de la segunda función. Dejar\(f : A \rightarrow B\) y\(g : B \rightarrow C\) ser mapeos. Definir un nuevo mapa, la composición de\(f\) y\(g\) de\(A\) a\(C\text{,}\) por\((g \circ f)(x) = g(f(x))\text{.}\)

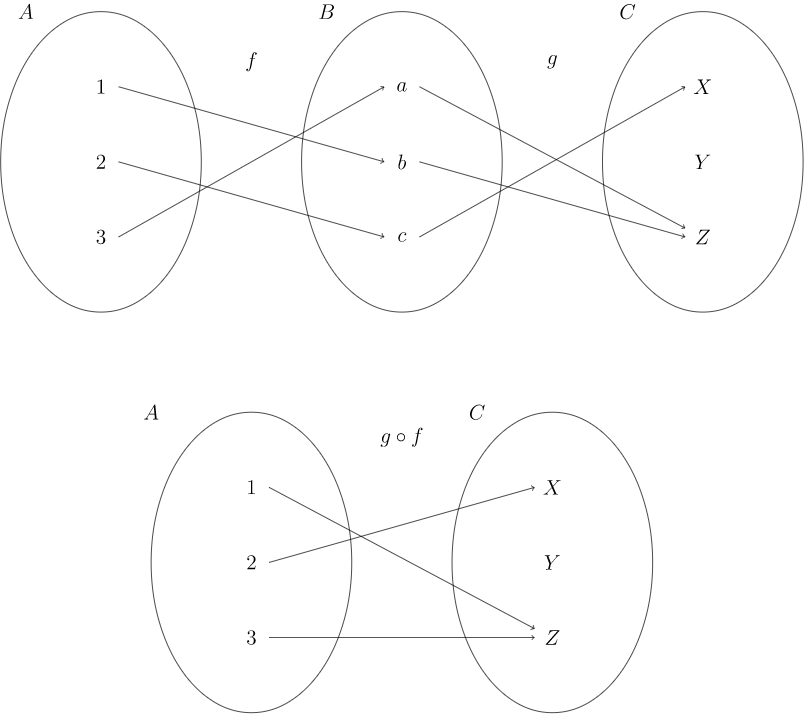
\(Figure \text { } 1.9\). Composición de mapas

Ejemplo\(1.10\)

Considere las funciones\(f: A \rightarrow B\) y\(g: B \rightarrow C\) que se definen en la Figura 1.9 (arriba).

Solución

La composición de estas funciones,\(g \circ f: A \rightarrow C\text{,}\) se define en la Figura 1.9 (abajo).

Ejemplo\(1.11\)

Let\(f(x) = x^2\) y\(g(x) = 2x + 5\text{.}\)

Solución

Entonces

\[ (f \circ g)(x) = f(g(x)) = (2x + 5)^2 = 4x^2 + 20x + 25 \nonumber \]

y

\[ (g \circ f)(x) = g(f(x)) = 2x^2 + 5\text{.} \nonumber \]

En general, el orden marca la diferencia; es decir, en la mayoría de los casos\(f \circ g \neq g \circ f\text{.}\)

Ejemplo\(1.12\)

A veces es el caso que\(f \circ g= g \circ f\text{.}\) Let\(f(x) = x^3\) y\(g(x) = \sqrt[3]{x}\text{.}\)

Solución

Entonces

\[ (f \circ g )(x) = f(g(x)) = f( \sqrt[3]{x}\, ) = (\sqrt[3]{x}\, )^3 = x \nonumber \]

y

\[ (g \circ f )(x) = g(f(x)) = g( x^3) = \sqrt[3]{ x^3} = x\text{.} \nonumber \]

Ejemplo\(1.13\)

Dada una\(2 \times 2\) matriz

\[ A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}\text{,} \nonumber \]

Solución

podemos definir un mapa\(T_A : {\mathbb R}^2 \rightarrow {\mathbb R}^2\) por

\[ T_A (x,y) = (ax + by, cx +dy) \nonumber \]

porque\((x,y)\) en\({\mathbb R}^2\text{.}\) Esto es en realidad multiplicación matricial; es decir,

\[ \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} ax + by \\ cx +dy \end{pmatrix}\text{.} \nonumber \]

Los mapas de\({\mathbb R}^n\) a\({\mathbb R}^m\) dados por matrices se denominan mapas lineales o transformaciones lineales.

Ejemplo\(1.14\)

Supongamos que\(S = \{ 1,2,3 \}\text{.}\) Definir un mapa\(\pi :S\rightarrow S\)

\[ \pi( 1 ) = 2, \qquad \pi( 2 ) = 1, \qquad \pi( 3 ) = 3\text{.} \nonumber \]

Solución

Se trata de un mapa biyectiva. Una forma alternativa de escribir\(\pi\) es

\[ \begin{pmatrix} 1 & 2 & 3 \\ \pi(1) & \pi(2) & \pi(3) \end{pmatrix} = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix}\text{.} \nonumber \]

Para cualquier conjunto,\(S\text{,}\) un mapeo uno a uno y en\(\pi : S \rightarrow S\) el mapeo se llama permutación de\(S\text{.}\)

Teorema\(1.15\)

Let\(f : A \rightarrow B\text{,}\)\(g : B \rightarrow C\text{,}\) y\(h : C \rightarrow D\text{.}\) Entonces

1. La composición de los mapeos es asociativa; es decir,\((h \circ g) \circ f = h \circ (g \circ f)\text{;}\)
2. Si\(f\) y\(g\) son ambos uno a uno, entonces el mapeo\(g \circ f\) es uno a uno;
3. Si\(f\) y\(g\) están ambos en, entonces el mapeo\(g \circ f\) está en;
4. Si\(f\) y\(g\) son biyectivos, entonces también lo es\(g \circ f\text{.}\)

Prueba

Vamos a probar (1) y (3). La parte (2) se deja como ejercicio. La parte (4) sigue directamente de (2) y (3).

(1) Debemos demostrar que

\[ h \circ (g \circ f) = (h \circ g) \circ f\text{.} \nonumber \]

Para\(a \in A\) nosotros tenemos

\ begin {align*} (h\ circ (g\ circ f)) (a) & = h ((g\ circ f) (a))\\ & = h (g (f (a)))\\ & = (h\ circ g) (f (a))\\ & = ((h\ circ g)\ circ f) (a)\ text {.} \ end {alinear*}

(3) Supongamos que\(f\) y ambos\(g\) están en funciones. Dado\(c \in C\text{,}\) debemos demostrar que existe\(a \in A\) tal que\((g \circ f)(a) = g(f(a)) = c\text{.}\) Sin embargo, ya que\(g\) está sobre, hay un elemento\(b \in B\) tal que\(g(b) = c\text{.}\) De igual manera, hay\(a \in A\) tal que\(f(a) = b\text{.}\) En consecuencia,

\[ (g \circ f)(a) = g(f(a)) = g(b) = c\text{.} \nonumber \]

Si\(S\) hay algún conjunto, usaremos\(id_S\) o\(id\) para denotar el mapeo de identidad de\(S\) a sí mismo. Definir este mapa por\(id(s) = s\) para todos\(s \in S\text{.}\) Un mapa\(g: B \rightarrow A\) es un mapeo inverso de\(f: A \rightarrow B\) si\(g \circ f = id_A\) y\(f \circ g = id_B\text{;}\) en otras palabras, la función inversa de una función simplemente “deshace” la función. Se dice que un mapa es invertible si tiene un inverso. Normalmente escribimos\(f^{-1}\) para la inversa de\(f\text{.}\)

Ejemplo\(1.16\)

La función\(f(x) = x^3\) tiene inversa\(f^{-1}(x) = \sqrt[3]{x}\) por Ejemplo 1.12.

Ejemplo\(1.17\)

El logaritmo natural y las funciones exponenciales,\(f(x) = \ln x\) y\(f^{-1}(x) = e^x\text{,}\) son inversos unos de otros siempre que seamos cuidadosos en la elección de dominios.

Solución

Observe que

\[ f(f^{-1}(x)) = f(e^x) = \ln e^x = x \nonumber \]

y

\[ f^{-1}(f(x)) = f^{-1}(\ln x) = e^{\ln x} = x \nonumber \]

siempre que la composición tenga sentido.

Ejemplo\(1.18\)

Supongamos que

\[ A = \begin{pmatrix} 3 & 1 \\ 5 & 2 \end{pmatrix}\text{.} \nonumber \]

Solución

Luego\(A\) define un mapa de\({\mathbb R}^2\) a\({\mathbb R}^2\) por

\[ T_A (x,y) = (3x + y, 5x + 2y)\text{.} \nonumber \]

Podemos encontrar un mapa inverso de\(T_A\) simplemente invirtiendo la matriz es\(A\text{;}\) decir,\(T_A^{-1} = T_{A^{-1}}\text{.}\) en este ejemplo,

\[ A^{-1} = \begin{pmatrix} 2 & -1 \\ -5 & 3 \end{pmatrix}; \nonumber \]

por lo tanto, el mapa inverso viene dado por

\[ T_A^{-1} (x,y) = (2x - y, -5x + 3y)\text{.} \nonumber \]

Es fácil verificar que

\[ T^{-1}_A \circ T_A (x,y) = T_A \circ T_A^{-1} (x,y) = (x,y)\text{.} \nonumber \]

No todos los mapas tienen una inversa. Si consideramos el mapa

\[ T_B (x,y) = (3x , 0 ) \nonumber \]

dada por la matriz

\[ B = \begin{pmatrix} 3 & 0 \\ 0 & 0 \end{pmatrix}\text{,} \nonumber \]

entonces un mapa inverso tendría que ser de la forma

\[ T_B^{-1} (x,y) = (ax + by, cx +dy) \nonumber \]

y

\[ (x,y) = T_B \circ T_B^{-1} (x,y) = (3ax + 3by, 0) \nonumber \]

para todos\(x\) y\(y\text{.}\) Claramente esto es imposible porque\(y\) podría no ser\(0\text{.}\)

Ejemplo\(1.19\)

Dada la permutación

\[ \pi = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} \nonumber \]

Solución

en\(S = \{ 1,2,3 \}\text{,}\) es fácil ver que la permutación definida por

\[ \pi^{-1} = \begin{pmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \end{pmatrix} \nonumber \]

es la inversa de\(\pi\text{.}\) De hecho, cualquier cartografía biyectiva posee una inversa, como veremos en el siguiente teorema.

Teorema\(1.20\)

Un mapeo es invertible si y solo si es tanto uno a uno como sobre.

Prueba

Supongamos primero que\(f:A \rightarrow B\) es invertible con inverso\(g: B \rightarrow A\text{.}\) Entonces\(g \circ f = id_A\) es el mapa de identidad; es decir,\(g(f(a)) = a\text{.}\) Si\(a_1, a_2 \in A\) con\(f(a_1) = f(a_2)\text{,}\) entonces\(a_1 = g(f(a_1)) = g(f(a_2)) = a_2\text{.}\) Consecuentemente,\(f\) es uno-a-uno. Ahora supongamos que\(b \in B\text{.}\) Para mostrar que\(f\) es sobre, es necesario encontrar un\(a \in A\) tal que\(f(a) = b\text{,}\) pero\(f(g(b)) = b\) con\(g(b) \in A\text{.}\) Let\(a = g(b)\text{.}\)

Por el contrario, dejemos\(f\) ser biyectiva y dejar\(b \in B\text{.}\) que Since\(f\) está en, existe\(a \in A\) tal que\(f(a) = b\text{.}\) Porque\(f\) es uno-a-uno,\(a\) debe ser único. Definir\(g\) dejando Ahora\(g(b) = a\text{.}\) hemos construido la inversa de\(f\text{.}\)

Relaciones de equivalencia y particiones

Una noción fundamental en matemáticas es la de igualdad. Podemos generalizar la igualdad con relaciones de equivalencia y clases de equivalencia. Una relación de equivalencia en un conjunto\(X\) es una relación\(R \subset X \times X\) tal que

• \((x, x) \in R\)para todos\(x \in X\) (propiedad reflexiva);
• \((x, y) \in R\)implica\((y, x) \in R\) (propiedad simétrica);
• \((x, y)\)e\((y, z) \in R\) implican\((x, z) \in R\) (propiedad transitiva).

Dada una relación de equivalencia\(R\) en un conjunto\(X\text{,}\) solemos escribir\(x \sim y\) en lugar de\((x, y) \in R\text{.}\) Si la relación de equivalencia ya tiene una notación asociada como\(=\text{,}\)\(\equiv\text{,}\) o\(\cong\text{,}\) usaremos esa notación.

Ejemplo\(1.21\)

Dejar\(p\text{,}\)\(q\text{,}\)\(r\text{,}\) y\(s\) ser enteros, donde\(q\) y\(s\) son distintos de cero. Definir\(p/q \sim r/s\) si\(ps = qr\text{.}\)

Solución

Claramente\(\sim\) es reflexivo y simétrico. Para demostrar que también es transitivo, supongamos que\(p/q \sim r/s\) y\(r/s \sim t/u\text{,}\) con\(q\text{,}\)\(s\text{,}\) y\(u\) todo distinto de cero. Entonces\(ps = qr\) y\(ru = st\text{.}\) Por lo tanto,

\[ psu = qru = qst\text{.} \nonumber \]

Dado que en\(s \neq 0\text{,}\)\(pu = qt\text{.}\) consecuencia,\(p/q \sim t/u\text{.}\)

Ejemplo\(1.22\)

Supongamos que\(f\) y\(g\) son funciones diferenciables en\({\mathbb R}\text{.}\) Podemos definir una relación de equivalencia en tales funciones dejando que\(f(x) \sim g(x)\) si\(f'(x) = g'(x)\text{.}\)

Solución

Es claro que\(\sim\) es tanto reflexivo como simétrico. Para demostrar la transitividad, supongamos que\(f(x) \sim g(x)\) y\(g(x) \sim h(x)\text{.}\) A partir del cálculo sabemos eso\(f(x) - g(x) = c_1\)\(c_1\) y\(g(x)- h(x) = c_2\text{,}\) dónde y\(c_2\) son ambas constantes. Por lo tanto,

\[ f(x) - h(x) = ( f(x) - g(x)) + ( g(x)- h(x)) = c_1 + c_2 \nonumber \]

y\(f'(x) - h'(x) = 0\text{.}\) Por lo tanto,\(f(x) \sim h(x)\text{.}\)

Ejemplo\(1.23\)

Para\((x_1, y_1 )\) y\((x_2, y_2)\) en\({\mathbb R}^2\text{,}\) definir\((x_1, y_1 ) \sim (x_2, y_2)\) si\(x_1^2 + y_1^2 = x_2^2 + y_2^2\text{.}\)

Solución

Entonces\(\sim\) es una relación de equivalencia sobre\({\mathbb R}^2\text{.}\)

Ejemplo\(1.24\)

Dejar\(A\) y\(B\) ser\(2 \times 2\) matrices con entradas en los números reales. Podemos definir una relación de equivalencia sobre el conjunto de\(2 \times 2\) matrices, diciendo\(A \sim B\) si existe una matriz invertible\(P\) tal que\(PAP^{-1} = B\text{.}\) Por ejemplo, si

\[ A = \begin{pmatrix} 1 & 2 \\ -1 & 1 \end{pmatrix} \quad \text{and} \quad B = \begin{pmatrix} -18 & 33 \\ -11 & 20 \end{pmatrix}\text{,} \nonumber \]

Solución

entonces\(A \sim B\) desde\(PAP^{-1} = B\) para

\[ P = \begin{pmatrix} 2 & 5 \\ 1 & 3 \end{pmatrix}\text{.} \nonumber \]

\(I\)Sea la matriz de\(2 \times 2\) identidad; es decir,

\[ I = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\text{.} \nonumber \]

Entonces,\(IAI^{-1} = IAI = A\text{;}\) por lo tanto, la relación es reflexiva. Para mostrar simetría, supongamos que\(A \sim B\text{.}\) Entonces existe una matriz invertible\(P\) tal\(PAP^{-1} = B\text{.}\) que So

\[ A = P^{-1} B P = P^{-1} B (P^{-1})^{-1}\text{.} \nonumber \]

Por último, supongamos que\(A \sim B\) y\(B \sim C\text{.}\) Entonces existen matrices invertibles\(P\) y\(Q\) tal que\(PAP^{-1} = B\) y\(QBQ^{-1} = C\text{.}\) Desde

\[ C = QBQ^{-1} = QPAP^{-1} Q^{-1} = (QP)A(QP)^{-1}\text{,} \nonumber \]

la relación es transitiva. Se dice que dos matrices que son equivalentes de esta manera son similares.

Una partición\({\mathcal P}\) de un conjunto\(X\) es una colección de conjuntos no vacíos de\(X_1, X_2, \ldots\) tal manera que\(X_i \cap X_j = \emptyset\) for\(i \neq j\) y\(\bigcup_k X_k = X\text{.}\) Let\(\sim\) be una relación de equivalencia en un conjunto\(X\) y let\(x \in X\text{.}\) Entonces\([x] = \{ y \in X : y \sim x \}\) se llama clase de equivalencia de\(x\text{.}\) Veremos que una relación de equivalencia da lugar a una partición vía clases de equivalencia. Además, siempre que existe una partición de un conjunto, existe alguna relación de equivalencia subyacente natural, como demuestra el siguiente teorema.

Teorema\(1.25\)

Dada una relación de equivalencia\(\sim\) en un conjunto\(X\text{,}\) las clases de equivalencia de\(X\) forman una partición de\(X\text{.}\) Inversamente, si\({\mathcal P} = \{ X_i\}\) es una partición de un conjunto\(X\text{,}\) entonces hay una relación de equivalencia\(X\) con clases de equivalencia\(X_i\text{.}\)

Prueba

Supongamos que existe una relación de equivalencia\(\sim\) en el conjunto\(X\text{.}\) Para cualquiera\(x \in X\text{,}\) la propiedad reflexiva muestra que\(x \in [x]\) y así\([x]\) es no vacía. Claramente\(X = \bigcup_{x \in X} [x]\text{.}\) Ahora vamos\(x, y \in X\text{.}\) Necesitamos demostrar que\([x] = [y]\) o bien\([x] \cap [y] = \emptyset\text{.}\) Supongamos que la intersección de\([x]\) y no\([y]\) está vacía y que\(z \in [x] \cap [y]\text{.}\) Entonces y\(z \sim y\text{.}\) Por simetría\(z \sim x\) y transitividad de\(x \sim y\text{;}\) ahí,\([x] \subset [y]\text{.}\) De igual manera,\([y] \subset [x]\) y así\([x] = [y]\text{.}\) pues, cualesquiera dos clases de equivalencia son o bien disjuntas o exactamente iguales.

Por el contrario, supongamos que\({\mathcal P} = \{X_i\}\) es una partición de un conjunto\(X\text{.}\) Dejar que dos elementos sean equivalentes si están en la misma partición. Claramente, la relación es reflexiva. Si\(x\) está en la misma partición como\(y\text{,}\) entonces\(y\) está en la misma partición como\(x\text{,}\) así\(x \sim y\) implica\(y \sim x\text{.}\) Finalmente, si\(x\) está en la misma partición que\(y\) y\(y\) está en la misma partición como\(z\text{,}\) entonces\(x\) debe estar en la misma partición como\(z\text{,}\) y se mantiene la transitividad.

Corolario\(1.26\)

Dos clases de equivalencia de una relación de equivalencia son disjuntas o iguales.

Examinemos algunas de las particiones dadas por las clases de equivalencia en el último conjunto de ejemplos.

Ejemplo\(1.27\)

En la relación de equivalencia del Ejemplo 1.21, dos pares de números enteros,\((p,q)\) y\((r,s)\text{,}\)

Solución

están en la misma clase de equivalencia cuando reducen a la misma fracción en sus términos más bajos.

Ejemplo\(1.28\)

En la relación de equivalencia del Ejemplo 1.22, dos funciones\(f(x)\) y\(g(x)\)

Solución

están en la misma partición cuando difieren por una constante.

Ejemplo\(1.29\)

Definimos una clase de equivalencia\({\mathbb R}^2\) por\((x_1, y_1 ) \sim (x_2, y_2)\) si\(x_1^2 + y_1^2 = x_2^2 + y_2^2\text{.}\)

Solución

Dos pares de números reales están en la misma partición cuando se encuentran en el mismo círculo alrededor del origen.

Ejemplo\(1.30\)

Dejar\(r\) y\(s\) ser dos enteros y supongamos que\(n \in {\mathbb N}\text{.}\) decimos que\(r\) es congruente con\(s\) modulo\(n\text{,}\) o\(r\) es congruente con\(s\) mod\(n\text{,}\) si\(r - s\) es uniformemente divisible por \(n\text{;}\)es decir,\(r - s = nk\) para algunos\(k \in {\mathbb Z}\text{.}\)

Solución

En este caso escribimos\(r \equiv s \pmod{n}\text{.}\) Por ejemplo,\(41 \equiv 17 \pmod{ 8}\) ya que\(41 - 17=24\) es divisible por\(8\text{.}\) Afirmamos que módulo de congruencia\(n\) forma una relación de equivalencia de\({\mathbb Z}\text{.}\) Ciertamente cualquier entero\(r\) es equivalente a sí mismo ya que\(r - r = 0\) es divisible por Ahora\(n\text{.}\) mostraremos que la relación es simétrica. Si\(r \equiv s \pmod{ n}\text{,}\) entonces\(r - s = -(s -r)\) es divisible por\(n\text{.}\) Así\(s - r\) es divisible por\(n\) y\(s \equiv r \pmod{ n}\text{.}\) Ahora supongamos que\(r \equiv s \pmod{ n}\) y\(s \equiv t \pmod{ n}\text{.}\) Entonces existen enteros\(k\) y\(l\) tal que\(r -s = kn\) y\(s - t = ln\text{.}\) Para mostrar la transitividad, es necesario probar que\(r - t\) es divisible por\(n\text{.}\) Sin embargo,

\[ r - t = r - s + s - t = kn + ln = (k + l)n\text{,} \nonumber \]

y así\(r - t\) es divisible por\(n\text{.}\)

Si consideramos la relación de equivalencia establecida por los enteros módulo\(3\text{,}\) entonces

\ begin {alinear*} {[0]} & =\ {\ ldots, -3, 0, 3, 6,\ ldots\},\\ {[1]} & =\ {\ ldots, -2, 1, 4, 7,\ ldots\},\\ {[2]} & =\ {\ ldots, -1, 2, 5, 8,\ ldots\}\ text {.} \ end {alinear*}

Observe eso\([0] \cup [1] \cup [2] = {\mathbb Z}\) y también que los conjuntos son desarticulados. Los conjuntos\([0]\text{,}\)\([1]\text{,}\) y\([2]\) forman una partición de los enteros.

Los enteros módulo\(n\) son un ejemplo muy importante en el estudio del álgebra abstracta y serán bastante útiles en nuestra investigación de diversas estructuras algebraicas como grupos y anillos. En nuestra discusión del módulo enteros\(n\) hemos asumido realmente un resultado conocido como el algoritmo de división, que será declarado y probado en el Capítulo 2.