4.1: Subgrupos cíclicos
- Page ID
- 111067
Muchas veces un subgrupo dependerá enteramente de un solo elemento del grupo; es decir, conocer ese elemento en particular nos permitirá computar cualquier otro elemento del subgrupo.
Supongamos que consideramos\(3 \in {\mathbb Z}\) y miramos todos los múltiplos (tanto positivos como negativos) de\(3\). Como conjunto, esto es
\[ 3 {\mathbb Z} = \{ \ldots, -3, 0, 3, 6, \ldots \}\text{.} \nonumber \]
Solución
Es fácil ver que\(3 {\mathbb Z}\) es un subgrupo de los enteros. Este subgrupo está completamente determinado por el elemento\(3\) ya que podemos obtener todos los demás elementos del grupo tomando múltiplos de\(3\text{.}\) Cada elemento en el subgrupo es “generado” por\(3\text{.}\)
Si\(H = \{ 2^n : n \in {\mathbb Z} \}\text{,}\)
Solución
entonces\(H\) es un subgrupo del grupo multiplicativo de números racionales distintos de cero,\({\mathbb Q}^*\text{.}\) Si\(a = 2^m\) y\(b = 2^n\) están en\(H\text{,}\) entonces también\(ab^{-1} = 2^m 2^{-n} = 2^{m-n}\) está en\(H\text{.}\) Por Proposición 3.31,\(H\) es un subgrupo de\({\mathbb Q}^*\) determinado por el elemento\(2\text{.}\)
Dejar\(G\) ser un grupo y\(a\) ser cualquier elemento en\(G\text{.}\) Luego el conjunto
\[ \langle a \rangle = \{ a^k : k \in {\mathbb Z} \} \nonumber \]
es un subgrupo de\(G\text{.}\) Además,\(\langle a \rangle\) es el subgrupo más pequeño del\(G\) que contiene\(a\text{.}\)
- Prueba
-
La identidad está en\(\langle a \rangle \) ya que\(a^0 = e\text{.}\) si\(g\) y\(h\) son cualesquiera dos elementos en\(\langle a \rangle \text{,}\) entonces por la definición de\(\langle a \rangle\) podemos escribir\(g = a^m\) y\(h = a^n\) para algunos enteros\(m\) y\(n\text{.}\) Así\(gh = a^m a^n = a^{m+n}\) es de nuevo en\(\langle a \rangle \text{.}\) Finalmente, si\(g = a^n\) en \(\langle a \rangle \text{,}\)entonces la inversa también\(g^{-1} = a^{-n}\) está en\(\langle a \rangle \text{.}\) Claramente, cualquier subgrupo\(H\) de\(G\) contener\(a\) debe contener todas las potencias de\(a\) por cierre; de ahí,\(H\) contiene\(\langle a \rangle \text{.}\) Por lo tanto,\(\langle a \rangle \) es el subgrupo más pequeño de\(G\) que contiene\(a\text{.}\)
Si estamos usando la notación “+”, como en el caso de los enteros en adición, escribimos\(\langle a \rangle = \{ na : n \in {\mathbb Z} \}\text{.}\)
Porque\(a \in G\text{,}\) llamamos\(\langle a \rangle \) al subgrupo cíclico generado por\(a\text{.}\) If\(G\) contiene algún elemento\(a\) tal que\(G = \langle a \rangle \text{,}\) entonces\(G\) es un grupo cíclico. En este caso\(a\) es un generador de\(G\text{.}\) Si\(a\) es un elemento de un grupo\(G\text{,}\) definimos el orden de\(a\) ser el entero positivo más pequeño\(n\) tal que\(a^n= e\text{,}\) y escribimos\(|a| = n\text{.}\) Si hay no es tal entero\(n\text{,}\) decimos que el orden de\(a\) es infinito y escribimos\(|a| = \infty\) para denotar el orden de\(a\text{.}\)
Observe que un grupo cíclico puede tener más de un solo generador. Ambos\(1\) y\(5\) generar\({\mathbb Z}_6\text{;}\)
Solución
por lo tanto,\({\mathbb Z}_6\) es un grupo cíclico. No todos los elementos de un grupo cíclico son necesariamente un generador del grupo. El orden de\(2 \in {\mathbb Z}_6\) es\(3\text{.}\) El subgrupo cíclico generado por\(2\) es\(\langle 2 \rangle = \{ 0, 2, 4 \}\text{.}\)
Los grupos\({\mathbb Z}\) y\({\mathbb Z}_n\) son grupos cíclicos. Los elementos\(1\) y\(-1\) son generadores para Ciertamente\({\mathbb Z}\text{.}\) podemos generar\({\mathbb Z}_n\) con 1 aunque puede haber otros generadores de\({\mathbb Z}_n\text{,}\) como en el caso de\({\mathbb Z}_6\text{.}\)
El grupo de unidades,\(U(9)\text{,}\) en\({\mathbb Z}_9\) es un grupo cíclico.
Solución
Como conjunto,\(U(9)\) es\(\{ 1, 2, 4, 5, 7, 8 \}\text{.}\) El elemento 2 es un generador para\(U(9)\) desde
\ begin {align*} 2^1 & = 2\ qquad 2^2 = 4\\ 2^3 & = 8\ qquad 2^4 = 7\\ 2^5 & = 5\ qquad 2^6 = 1\ text {.} \ end {alinear*}
No todos los grupos son un grupo cíclico. Considerar el grupo de simetría de un triángulo equilátero\(S_3\text{.}\) La tabla de multiplicación para este grupo es\(Figure \text { } 3.7\).
Solución
Los subgrupos de\(S_3\) se muestran en\(Figure \text { } 4.8\). Observe que cada subgrupo es cíclico; sin embargo, ningún elemento genera todo el grupo.
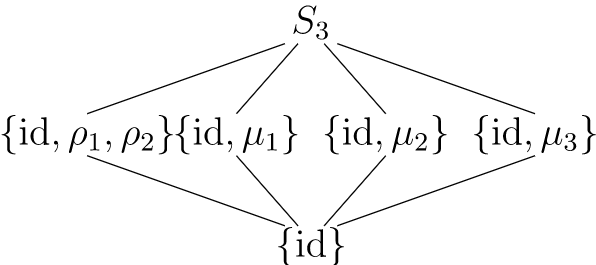
\(Figure \text { } 4.8.\)Subgrupos de\(S_3\)
Cada grupo cíclico es abeliano.
- Prueba
-
Dejar\(G\) ser un grupo cíclico y\(a \in G\) ser un generador para\(G\text{.}\) Si\(g\) y\(h\) están en\(G\text{,}\) entonces se pueden escribir como poderes de\(a\text{,}\) decir\(g = a^r\) y\(h = a^s\text{.}\) desde
\[ g h = a^r a^s = a^{r+s} = a^{s+r} = a^s a^r = h g\text{,} \nonumber \]
\(G\)es abeliano.
Subgrupos de grupos cíclicos
Podemos hacer algunas preguntas interesantes sobre los subgrupos cíclicos de un grupo y los subgrupos de un grupo cíclico. Si\(G\) es un grupo, ¿qué subgrupos de\(G\) son cíclicos? Si\(G\) es un grupo cíclico, ¿qué tipo de subgrupos\(G\) posee?
Cada subgrupo de un grupo cíclico es cíclico.
- Prueba
-
Las principales herramientas utilizadas en esta prueba son el algoritmo de división y el Principio de Ordenamiento Bien. Dejar\(G\) ser un grupo cíclico generado por\(a\) y supongamos que\(H\) es un subgrupo de\(G\text{.}\) Si\(H = \{ e \}\text{,}\) entonces trivialmente\(H\) es cíclico. Supongamos que\(H\) contiene algún otro elemento\(g\) distinto de la identidad. Entonces se\(g\) puede escribir como\(a^n\) para algún entero\(n\text{.}\) ya que\(H\) es un subgrupo, también\(g^{-1} = a^{-n}\) debe estar en\(H\text{.}\) Dado que ya sea\(n\) o\(-n\) es positivo, podemos suponer que\(H\) contiene potencias positivas de\(a\) y\(n \gt 0\text{.}\) Let \(m\)ser el número natural más pequeño tal que\(a^m \in H\text{.}\) Tal\(m\) existe por el Principio de Ordenamiento Bien.
Afirmamos que\(h = a^m\) es un generador para\(H\text{.}\) Debemos demostrar que cada uno\(h' \in H\) puede escribirse como un poder de\(h\text{.}\)\(h' \in H\) Since y\(H\) es un subgrupo de\(G\text{,}\)\(h' = a^k\) para algún entero\(k\text{.}\) Usando el algoritmo de división, podemos encontrar números\(q\) y \(r\)de tal manera que\(k = mq +r\) donde\(0 \leq r \lt m\text{;}\) por lo tanto,
\[ a^k = a^{mq +r} = (a^m)^q a^r = h^q a^r\text{.} \nonumber \]
Por lo tanto,\(a^r = a^k h^{-q}\text{.}\) ya que\(a^k\)\(h^{-q}\) están en\(H\text{,}\)\(a^r\) debe estar también en\(H\text{.}\) Sin embargo,\(m\) fue el número positivo más pequeño tal que\(a^m\) estaba en\(H\text{;}\) consecuencia,\(r=0\) y así\(k=mq\text{.}\) Por lo tanto,
\[ h' = a^k = a^{mq} = h^q \nonumber \]
y\(H\) es generado por\(h\text{.}\)
Los subgrupos de\({\mathbb Z}\) son exactamente\(n{\mathbb Z}\) para\(n = 0, 1, 2,\ldots\text{.}\)
Dejar\(G\) ser un grupo cíclico de orden\(n\) y supongamos que\(a\) es un generador para\(G\text{.}\) Entonces\(a^k=e\) si y solo si\(n\) divide\(k\text{.}\)
- Prueba
-
Primero supongamos que\(a^k=e\text{.}\) Por el algoritmo de división,\(k = nq + r\) donde de\(0 \leq r \lt n\text{;}\) ahí,
\[ e = a^k = a^{nq + r} = a^{nq} a^r = e a^r = a^r\text{.} \nonumber \]
Dado que el entero positivo más pequeño\(m\) tal que\(a^m = e\) es\(n\text{,}\)\(r= 0\text{.}\)
Por el contrario, si\(k\text{,}\) se\(n\) divide entonces\(k=ns\) para algún entero\(s\text{.}\) En consecuencia,
\[ a^k = a^{ns} = (a^n)^s = e^s = e\text{.} \nonumber \]
Dejar\(G\) ser un grupo cíclico de orden\(n\) y supongamos que\(a \in G\) es un generador del grupo. Si\(b = a^k\text{,}\) entonces el orden de\(b\) es\(n/d\text{,}\) donde\(d = \gcd(k,n)\text{.}\)
- Prueba
-
Deseamos encontrar el entero más pequeño\(m\) tal que\(e = b^m = a^{km}\text{.}\) Por la Proposición 4.12, este es el entero más pequeño\(m\) tal que\(n\) divide\(km\) o, equivalentemente,\(n/d\) divide\(m(k/d)\text{.}\) Dado que\(d\) es el mayor divisor común de\(n\) y\(k\text{,}\) \(n/d\)y\(k/d\) son relativamente primos. De ahí\(n/d\) que para\(m(k/d)\) dividirlo debe dividir\(m\text{.}\) El más pequeño tal\(m\) es\(n/d\text{.}\)
Los generadores de\({\mathbb Z}_n\) son los enteros\(r\) tales que\(1 \leq r \lt n\) y\(\gcd(r,n) = 1\text{.}\)
Examinemos el grupo\({\mathbb Z}_{16}\text{.}\)
Solución
Los números\(1\text{,}\)\(3\text{,}\)\(5\text{,}\)\(7\text{,}\)\(9\text{,}\)\(11\text{,}\)\(13\text{,}\) y\(15\) son los elementos de\({\mathbb Z}_{16}\) que son relativamente primos a\(16\text{.}\) Cada uno de estos elementos genera\({\mathbb Z}_{16}\text{.}\) Por ejemplo,
\ begin {align*} 1\ cdot 9 & = 9 & 2\ cdot 9 & = 2 & 3\ cdot 9 & = 11\\ 4\ cdot 9 & = 4 & 5\ cdot 9 & = 13 & 6\ cdot 9 & = 6\\ 7\ cdot 9 & = 15 & 8\ cdot 9 & = 8 & 9\ cdot 9 & = 1\\ 10\ cdot 9 & = 10 & 11\ cdot 9 & = 3 & 12\ cdot 9 & = 12\\ 13\ cdot 9 & = 5 & 14\ cdot 9 & = 14 & 15\ cdot 9 & = 7\ texto {.} \ end {alinear*}


