8.2: Códigos de Detección y Corrección de Errores

Última actualización
Guardar como PDF

Page ID: 111128

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Examinemos un modelo sencillo de un sistema de comunicaciones para transmitir y recibir mensajes codificados (Figura$8.1$).

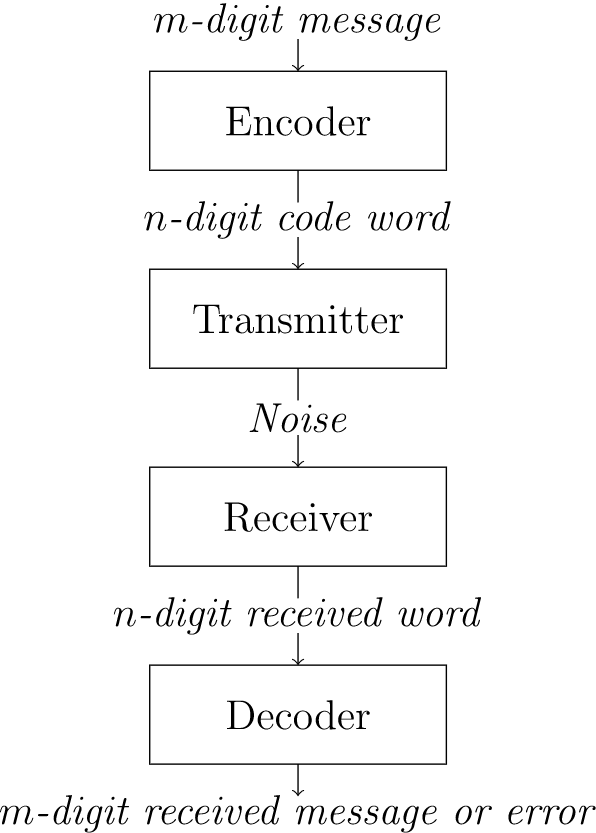
$clipboard_e212a461f2e1f43628316e18a086a05d3.png$

$Figure \text { } 8.1.$Codificación y decodificación de mensajes

Los mensajes no codificados pueden estar compuestos por letras o caracteres, pero normalmente consisten en$m$ -tuplas binarias. Estos mensajes son codificados en palabras de código, que consisten en$n$ -tuplas binarias, por un dispositivo llamado codificador. El mensaje se transmite y luego se descodifica. Consideraremos la ocurrencia de errores durante la transmisión. Se produce un error si hay un cambio en uno o más bits en la palabra de código. Un esquema de decodificación es un método que convierte una$n$ tupla recibida arbitrariamente en un mensaje decodificado significativo o da un mensaje de error para esa$n$ -tupla. Si el mensaje recibido es una palabra de código (una de las$n$ tuplas especiales permitidas para ser transmitidas), entonces el mensaje decodificado debe ser el mensaje único que se codificó en la palabra de código. Para las palabras no codificadas recibidas, el esquema de decodificación dará una indicación de error, o, si somos más inteligentes, intentará corregir el error y reconstruir el mensaje original. Nuestro objetivo es transmitir mensajes libres de errores de la manera más barata y rápida posible.

Ejemplo$8.2$

Un posible esquema de codificación sería enviar un mensaje varias veces y comparar las copias recibidas entre sí. Supongamos que el mensaje a codificar es una$n$ -tupla binaria$(x_{1}, x_{2}, \ldots, x_{n})\text{.}$ El mensaje se codifica en una$3n$ -tupla binaria simplemente repitiendo el mensaje tres veces:

\[ (x_{1}, x_{2}, \ldots, x_{n}) \mapsto (x_{1}, x_{2}, \ldots, x_{n}, x_{1}, x_{2}, \ldots, x_{n}, x_{1}, x_{2}, \ldots, x_{n})\text{.} \nonumber \]

Solución

Para decodificar el mensaje, elegimos como dígito$i$ th el que aparece en el lugar$i$ th en al menos dos de las tres transmisiones. Por ejemplo, si el mensaje original es$(0110)\text{,}$ entonces el mensaje transmitido será$(0110\; 0110\; 0110)\text{.}$ Si hay un error de transmisión en el quinto dígito, entonces la palabra clave recibida será la$(0110\; 1110\; 0110)\text{,}$ que se decodificará correctamente como$(0110)\text{.}$ ³ Este método de triple repetición automáticamente detectar y corregir todos los errores individuales, pero es lento e ineficiente: para enviar un mensaje que consiste en$n$ bits, se requieren bits$2n$ adicionales, y solo podemos detectar y corregir errores individuales. Veremos que es posible encontrar un esquema de codificación que codificará un mensaje de$n$ bits en$m$ bits con$m$ mucho menor que$3n\text{.}$

Ejemplo$8.3$

Incluso la paridad, un esquema de codificación de uso común, es mucho más eficiente que el esquema de repetición simple. El sistema de codificación ASCII (American Standard Code for Information Interchange) utiliza$8$ -tuplas binarias, produciendo$2^{8} = 256$ posibles$8$ -tuplas. Sin embargo, solo se necesitan siete bits ya que solo hay caracteres$2^7 = 128$ ASCII. ¿Qué se puede o se debe hacer con el bit extra?

Solución

Usando los ocho bits completos, podemos detectar errores de transmisión única. Por ejemplo, los códigos ASCII para A, B y C son

\ begin {alinear*}\ texto {A} & = 65_ {10} = 01000001_ {2},\\ texto {B} & = 66_ {10} = 01000010_ {2},\\ texto {C} & = 67_ {10} = 01000011_ {2}\ texto {.} \ end {align*}

Observe que el bit más a la izquierda siempre se establece en 0; es decir, los caracteres$128$ ASCII tienen códigos

\ begin {alinear*} 00000000_ {2} & = 0_ {10},\\ &\ vdots\\ 011111_ {2} & = 127_ {10}\ text {.} \ end {align*}

El bit se puede utilizar para la comprobación de errores en los otros siete bits. Se establece en uno$0$ o para$1$ que el número total de$1$ bits en la representación de un carácter sea par. Usando paridad par, los códigos para A, B y C ahora se convierten

\ begin {alinear*}\ texto {A} & = 01000001_ {2},\\\ texto {B} & = 01000010_ {2},\\ texto {C} & = 11000011_ {2}\ texto {.} \ end {align*}

Supongamos que se envía una A y un error de transmisión en el sexto bit es causado por ruido sobre el canal de comunicación para que$(0100\; 0101)$ se reciba. Sabemos que se ha producido un error ya que la palabra recibida tiene un número impar de$1$ s, y ahora podemos solicitar que la palabra clave se transmita nuevamente. Cuando se usa para la comprobación de errores, el bit más a la izquierda se denomina bit de verificación de paridad.

Con mucho, los códigos de detección de errores más comunes utilizados en las computadoras se basan en la adición de un bit de paridad. Por lo general, una computadora almacena información en$m$ -tuplas llamadas palabras. Las longitudes de palabras comunes son$8\text{,}$$16\text{,}$ y$32$ bits. Un bit en la palabra se deja de lado como el bit de verificación de paridad, y no se usa para almacenar información. Este bit se establece en cualquiera$0$ o$1\text{,}$ dependiendo del número de$1$ s en la palabra.

Agregar un bit de verificación de paridad permite la detección de todos los errores individuales porque cambiar un solo bit aumenta o disminuye el número de$1$ s en uno, y en cualquier caso la paridad se ha cambiado de par a impar, por lo que la nueva palabra no es una palabra clave. (También podríamos construir un esquema de detección de errores basado en paridad impar; es decir, podríamos establecer el bit de verificación de paridad para que una palabra clave siempre tenga un número impar de$1$ s.)

El sistema de paridad uniforme es fácil de implementar, pero tiene dos inconvenientes. Primero, los errores múltiples no son detectables. Supongamos que se envía una A y los bits primero y séptimo se cambian de$0$ a$1\text{.}$ La palabra recibida es una palabra clave, pero se decodificará en una C en lugar de una A. En segundo lugar, no tenemos la capacidad de corregir errores. Si$(1001\; 1000)$ se recibe la 8-tupla, sabemos que se ha producido un error, pero no tenemos idea de qué bit se ha cambiado. Ahora investigaremos un esquema de codificación que no sólo nos permitirá detectar errores de transmisión sino que en realidad corregirá los errores.

Ejemplo$8.4$

Supongamos que nuestro mensaje original es a$0$ o a$1\text{,}$ y que$0$ codifica$(000)$ y$1$ codifica para$(111)\text{.}$

Solución

Si solo ocurre un solo error durante la transmisión, podemos detectar y corregir el error. Por ejemplo, si$(101)$ se recibe a, entonces el segundo bit debe haber sido cambiado de$1$ a a$0\text{.}$ La palabra de código originalmente transmitida debe haber sido$(111)\text{.}$ Este método detectará y corregirá todos los errores individuales.

$Table \text { } 8.5$. Un código de repetición

Transmitido	Palabra recibida
Palabra de código	$000$	$001$	$010$	$011$	$100$	$101$	$110$	$111$
$000$	$0$	$1$	$1$	$2$	$1$	$2$	$2$	$3$
$111$	$3$	$2$	$2$	$1$	$2$	$1$	$1$	$0$

En Table$8.5$, presentamos todas las palabras posibles que podrían recibirse para las palabras de código transmitidas$(000)$ y$(111)\text{.}$ Table$8.5$ también muestra el número de bits por los cuales cada$3$ -tupla recibida difiere de cada palabra de código original.

Decodificación de máxima probabilidad

El esquema de codificación presentado en Ejemplo no$8.4$ es una solución completa al problema porque no tiene en cuenta la posibilidad de múltiples errores. Por ejemplo, se podría enviar un (000) o un (111) y recibir un (001). No tenemos medios para decidir a partir de la palabra recibida si hubo un solo error en el tercer bit o dos errores, uno en el primer bit y otro en el segundo. No importa qué esquema de codificación se utilice, se podría recibir un mensaje incorrecto. Podríamos transmitir a (000), tener errores en los tres bits y recibir la palabra clave (111). Es importante hacer suposiciones explícitas sobre la probabilidad y distribución de errores de transmisión para que, en una aplicación particular, se sepa si un esquema de detección de errores dado es apropiado. Supondremos que los errores de transmisión son raros, y, que cuando ocurren, ocurren independientemente en cada bit; es decir, si$p$ es la probabilidad de un error en un bit y$q$ es la probabilidad de un error en un bit diferente, entonces la probabilidad de que ocurran errores en ambos bits al mismo tiempo es También$pq\text{.}$ asumiremos que una$n$ -tupla recibida se decodifica en una palabra de código que está más cerca de ella; es decir, suponemos que el receptor utiliza decodificación de máxima verosimilitud. ⁴

Esta sección requiere un conocimiento de probabilidad, pero se puede omitir sin pérdida de continuidad.

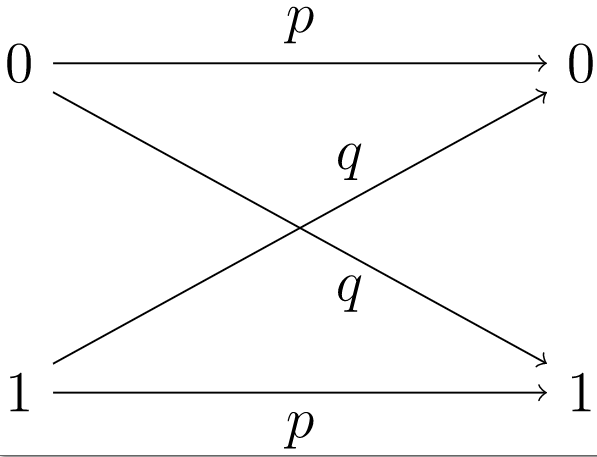
$Figure \text { } 8.6.$Canal simétrico binario

Un canal simétrico binario es un modelo que consiste en un transmisor capaz de enviar una señal binaria, ya sea a$0$ o a$1\text{,}$ junto con un receptor. $p$Sea la probabilidad de que la señal se reciba correctamente. Entonces$q = 1 - p$ es la probabilidad de una recepción incorrecta. Si$1$ se envía a, entonces la probabilidad de que$1$ se reciba a es$p$ y la probabilidad de que$0$ se reciba a es$q$ (Figura$8.6$). La probabilidad de que no ocurran errores durante la transmisión de una palabra de código binaria de longitud$n$ es$p^{n}\text{.}$ Por ejemplo, si$p=0.999$ y se envía un mensaje que consta de 10,000 bits, entonces la probabilidad de una transmisión perfecta es

\[ (0.999)^{10,000} \approx 0.00005\text{.} \nonumber \]

Teorema$8.7$

Si$(x_{1}, \ldots, x_{n})$ se transmite una$n$ tupla binaria a través de un canal simétrico binario con probabilidad de$p$ que no se produzca ningún error en cada coordenada, entonces la probabilidad de que haya errores en las$k$ coordenadas exactamente es

\[ \binom{n}{k} q^kp^{n - k}\text{.} \nonumber \]

Prueba

Arreglar$k$ diferentes coordenadas. Primero calculamos la probabilidad de que se haya producido un error en este conjunto fijo de coordenadas. La probabilidad de que ocurra un error en una determinada de estas$k$ coordenadas es$q\text{;}$ la probabilidad de que no ocurra un error en ninguna de las$n-k$ coordenadas restantes es$p\text{.}$ La probabilidad de cada uno de estos eventos$n$ independientes es$q^{k}p^{n-k}\text{.}$ El número de posibles patrones de error con exactamente$k$ errores que ocurren es igual a

\[ \binom{n}{k} = \frac{n!}{k!(n - k)!}\text{,} \nonumber \]

el número de combinaciones de$n$ cosas tomadas$k$ a la vez. Cada uno de estos patrones de error tiene probabilidad$q^{k}p^{n-k}$ de ocurrir; por lo tanto, la probabilidad de todos estos patrones de error es

\[ \binom{n}{k} q^{k}p^{n - k}\text{.} \nonumber \]

Ejemplo$8.8$

Supongamos que$p = 0.995$ y se envía$500$ un mensaje -bit.

Solución

La probabilidad de que el mensaje se haya enviado sin errores es

\[ p^{n} = (0.995)^{500} \approx 0.082\text{.} \nonumber \]

La probabilidad de que ocurra exactamente un error es

\[ \binom{n}{1} qp^{n - 1}= 500(0.005)(0.995)^{499} \approx 0.204\text{.} \nonumber \]

La probabilidad de exactamente dos errores es

\[ \binom{n}{2} q^{2}p^{n - 2}= \frac{500 \cdot 499}{2}(0.005)^{2}(0.995)^{498} \approx 0.257\text{.} \nonumber \]

La probabilidad de más de dos errores es aproximadamente

\[ 1 - 0.082 - 0.204 - 0.257 = 0.457\text{.} \nonumber \]

Códigos de bloque

Si queremos desarrollar códigos eficientes de detección y corrección de errores, necesitaremos herramientas matemáticas más sofisticadas. La teoría de grupos permitirá métodos más rápidos de codificación y decodificación de mensajes. Un código es un$(n, m)$ - código de bloque si la información que se va a codificar puede dividirse en bloques de dígitos$m$ binarios, cada uno de los cuales se puede codificar en dígitos$n$ binarios. Más específicamente, un código$(n, m)$ -block consiste en una función de codificación

\[ E:{\mathbb Z}^{m}_{2} \rightarrow {\mathbb Z}^{n}_{2} \nonumber \]

y una función de decodificación

\[ D:{\mathbb Z}^{n}_{2} \rightarrow {\mathbb Z}^{m}_{2}\text{.} \nonumber \]

Una palabra clave es cualquier elemento en la imagen de También$E\text{.}$ requerimos que$E$ sea uno a uno para que dos bloques de información no sean codificados en la misma palabra de código. Si nuestro código va a ser corrector de errores, entonces$D$ debe estar encendido.

Ejemplo$8.9$

El sistema de codificación de paridad par desarrollado para detectar errores individuales en caracteres ASCII es un código$(8,7)$ -block.

Solución

La función de codificación es

\[ E(x_7, x_6, \ldots, x_1) = (x_8, x_7, \ldots, x_1)\text{,} \nonumber \]

donde$x_8 = x_7 + x_6 + \cdots + x_1$ con adición en${\mathbb Z}_2\text{.}$

Dejar${\mathbf x} = (x_1, \ldots, x_n)$ y${\mathbf y} = (y_1, \ldots, y_n)$ ser binarios$n$ -tuplas. La distancia o distancia de Hamming,$d({\mathbf x}, {\mathbf y})\text{,}$ entre${\mathbf x}$ y${\mathbf y}$ es el número de bits en los que${\mathbf x}$ y${\mathbf y}$ difieren. La distancia entre dos palabras de código es el número mínimo de errores de transmisión requeridos para cambiar una palabra de código en la otra. La distancia mínima para un código,$d_{\min}\text{,}$ es la mínima de todas las distancias$d({\mathbf x}, {\mathbf y})\text{,}$ donde${\mathbf x}$ y${\mathbf y}$ son palabras clave distintas. El peso,$w({\mathbf x})\text{,}$ de una palabra de código binario${\mathbf x}$ es el número de$1$ s en${\mathbf x}\text{.}$ Claramente,$w({\mathbf x}) = d({\mathbf x}, {\mathbf 0})\text{,}$ donde${\mathbf 0} = (00 \cdots 0)\text{.}$

Ejemplo$8.10$

Dejar${\mathbf x} = (10101)\text{,}$${\mathbf y} = (11010)\text{,}$ y${\mathbf z} = (00011)$ ser todas las palabras de código en algún código$C\text{.}$

Solución

Entonces tenemos las siguientes distancias Hamming:

\[ d({\mathbf x},{\mathbf y}) = 4, \qquad d({\mathbf x},{\mathbf z}) = 3, \qquad d({\mathbf y},{\mathbf z}) = 3\text{.} \nonumber \]

La distancia mínima para este código es 3. También contamos con los siguientes pesos:

\[ w({\mathbf x}) = 3, \qquad w({\mathbf y}) = 3, \qquad w({\mathbf z}) = 2\text{.} \nonumber \]

La siguiente proposición enumera algunas propiedades básicas sobre el peso de una palabra de código y la distancia entre dos palabras de código. La prueba se deja como ejercicio.

Proposición$8.11$

Dejar${\mathbf x}\text{,}$${\mathbf y}\text{,}$ y${\mathbf z}$ ser binarios$n$ -tuplas. Entonces

$w({\mathbf x}) = d( {\mathbf x}, {\mathbf 0})\text{;}$
$d( {\mathbf x}, {\mathbf y}) \geq 0\text{;}$
$d( {\mathbf x}, {\mathbf y}) = 0$exactamente cuando${\mathbf x} = {\mathbf y}\text{;}$
$d( {\mathbf x}, {\mathbf y})= d( {\mathbf y}, {\mathbf x})\text{;}$
$d( {\mathbf x}, {\mathbf y}) \leq d( {\mathbf x}, {\mathbf z}) + d( {\mathbf z}, {\mathbf y})\text{.}$

$Table \text { } 8.12.$Distancias entre palabras de código de 4 bits

	$0000$	$0011$	$0101$	$0110$	$1001$	$1010$	$1100$	$1111$
$0000$	$0$	$2$	$2$	$2$	$2$	$2$	$2$	$4$
$0011$	$2$	$0$	$2$	$2$	$2$	$2$	$4 $	$2$
$0101$	$2$	$2$	$0$	$2$	$2$	$4$	$2$	$2$
$0110$	$2$	$2$	$2$	$0$	$4$	$2$	$2$	$2$
$1001$	$2$	$2$	$2$	$4$	$0$	$2$	$2$	$2$
$1010$	$2$	$2$	$4$	$2$	$2$	$0$	$2$	$2$
$1100$	$2$	$4$	$2$	$2$	$2$	$2$	$0$	$2$
$1111$	$4$	$2$	$2$	$2$	$2$	$2$	$2$	$0$

Los pesos en un código en particular suelen ser mucho más fáciles de calcular que las distancias Hamming entre todas las palabras de código en el código. Si un código se configura con cuidado, podemos aprovechar este hecho para nuestro beneficio.

Supongamos que${\mathbf x} = (1101)$ y${\mathbf y} = (1100)$ son palabras de código en algún código. Si transmitimos$(1101)$ y se produce un error en el bit más a la derecha, entonces se recibirá (1100). Dado que$(1100)$ es una palabra de código, el decodificador se descodificará$(1100)$ como el mensaje transmitido. Este código claramente no es muy apropiado para la detección de errores. El problema es que$d({\mathbf x}, {\mathbf y}) = 1\text{.}$ Si${\mathbf x} = (1100)$ y${\mathbf y} = (1010)$ son palabras de código, entonces$d({\mathbf x}, {\mathbf y}) = 2\text{.}$ Si${\mathbf x}$ se transmite y se produce un solo error, entonces nunca se${\mathbf y}$ puede recibir. Tabla$8.12$ da las distancias entre todas las palabras de código de 4 bits en las que los tres primeros bits llevan información y el cuarto es un bit de comprobación de paridad par. Podemos ver que la distancia mínima aquí es$2\text{;}$ por lo tanto, el código es adecuado como un solo código de detección de errores.

Para determinar exactamente cuáles son las capacidades de detección y corrección de errores para un código, necesitamos analizar la distancia mínima para el código. Dejar${\mathbf x}$ y${\mathbf y}$ ser palabras clave. Si$d({\mathbf x}, {\mathbf y}) = 1$ y se produce un error donde${\mathbf x}$ y${\mathbf y}$ difieren, entonces${\mathbf x}$ se cambia a${\mathbf y}\text{.}$ La palabra de código recibida es${\mathbf y}$ y no se da ningún mensaje de error. Ahora supongamos$d({\mathbf x}, {\mathbf y}) = 2\text{.}$ Entonces un solo error no puede cambiar${\mathbf x}$ a${\mathbf y}\text{.}$ Por lo tanto, si$d_{\min} = 2\text{,}$ tenemos la capacidad de detectar errores únicos. Sin embargo, supongamos que$d({\mathbf x}, {\mathbf y}) = 2\text{,}$${\mathbf y}$ se envía, y${\mathbf z}$ se recibe una palabra sin código de tal manera que

\[ d({\mathbf x}, {\mathbf z}) = d({\mathbf y}, {\mathbf z}) = 1\text{.} \nonumber \]

Entonces el decodificador no puede decidir entre${\mathbf x}$ y A${\mathbf y}\text{.}$ pesar de que somos conscientes de que se ha producido un error, no sabemos cuál es el error.

Supongamos$d_{\min} \geq 3\text{.}$ Entonces el esquema de decodificación de máxima probabilidad corrige todos los errores individuales. Comenzando con una palabra clave${\mathbf x}\text{,}$ un error en la transmisión de un solo bit da${\mathbf y}$ con$d({\mathbf x}, {\mathbf y}) = 1\text{,}$ pero$d({\mathbf z}, {\mathbf y}) \geq 2$ para cualquier otra palabra de código${\mathbf z} \neq {\mathbf x}\text{.}$ Si no requerimos la corrección de errores, entonces podemos detectar múltiples errores cuando un código tiene una distancia mínima que es mayor o igual a$3\text{.}$

Teorema$8.13$

Let$C$ be a code with$d_{\min} = 2n + 1\text{.}$ Then$C$ puede corregir cualquiera$n$ o menos errores. Además, se pueden detectar cualquiera$2n$ o menos errores en$C\text{.}$

Prueba

Supongamos que${\mathbf x}$ se envía una palabra clave y la palabra${\mathbf y}$ se recibe con como máximo$n$ errores. Entonces,$d( {\mathbf x}, {\mathbf y}) \leq n\text{.}$ si${\mathbf z}$ hay alguna palabra de código que no sea${\mathbf x}\text{,}$ entonces

\[ 2n+1 \leq d( {\mathbf x}, {\mathbf z}) \leq d( {\mathbf x}, {\mathbf y}) + d( {\mathbf y}, {\mathbf z}) \leq n + d( {\mathbf y}, {\mathbf z})\text{.} \nonumber \]

De ahí,$d({\mathbf y}, {\mathbf z} ) \geq n+1$ y se${\mathbf y}$ decodificará correctamente como${\mathbf x}\text{.}$ Ahora supongamos que${\mathbf x}$ se transmite y${\mathbf y}$ se recibe y que al menos se ha producido un error, pero no más que$2n$ errores. Entonces$1 \leq d( {\mathbf x}, {\mathbf y} ) \leq 2n\text{.}$ Dado que la distancia mínima entre las palabras de código$2n +1\text{,}$${\mathbf y}$ no puede ser una palabra de código. En consecuencia, el código puede detectar entre$1$ y$2n$ errores.

Ejemplo$\PageIndex{1}$

En Tabla$8.15$, las palabras de código${\mathbf c}_1 = (00000)\text{,}$${\mathbf c}_2 = (00111)\text{,}$${\mathbf c}_3 = (11100)\text{,}$ y${\mathbf c}_4 = (11011)$ determinar un solo código de corrección de errores.

Solución

$Table \text { } 8.15.$Distancias de Hamming para un código de corrección de errores

	$00000$	$00111$	$11100$	$11011$
$00000 $	$0$	$3$	$3$	$4$
$00111 $	$3$	$0$	$4$	$3$
$11100 $	$3$	$4$	$0$	$3$
$11011 $	$4$	$3$	$3$	$0$

Nota Histórica

La teoría moderna de la codificación comenzó en 1948 con el artículo de C. Shannon, “A Mathematical Theory of Information” [7]. Este artículo ofreció un ejemplo de un código algebraico, y el Teorema de Shannon proclamó exactamente cuán buenos podrían esperarse que fueran los códigos. Richard Hamming comenzó a trabajar con códigos lineales en Bell Labs a finales de los años 40 y principios de los 50 después de sentirse frustrado porque los programas que estaba ejecutando no podían recuperarse de simples errores generados por el ruido. La teoría de la codificación ha crecido enormemente en las últimas décadas. La Teoría de los Códigos Correctores de Errores, de MacWilliams y Sloane [5], publicada en 1977, ya contenía más de 1500 referencias. Se utilizaron códigos lineales (códigos de$(32, 6)$ bloque Reed-Muller) en las sondas espaciales Mariner de la NASA. Las sondas espaciales más recientes como Voyager han utilizado lo que se llama códigos de convolución. Actualmente, se está realizando una investigación muy activa con los códigos Goppa, que dependen en gran medida de la geometría algebraica.

Transmitido	Palabra recibida
Palabra de código	\(000\)	\(001\)	\(010\)	\(011\)	\(100\)	\(101\)	\(110\)	\(111\)
\(000\)	\(0\)	\(1\)	\(1\)	\(2\)	\(1\)	\(2\)	\(2\)	\(3\)
\(111\)	\(3\)	\(2\)	\(2\)	\(1\)	\(2\)	\(1\)	\(1\)	\(0\)

	\(0000\)	\(0011\)	\(0101\)	\(0110\)	\(1001\)	\(1010\)	\(1100\)	\(1111\)
\(0000\)	\(0\)	\(2\)	\(2\)	\(2\)	\(2\)	\(2\)	\(2\)	\(4\)
\(0011\)	\(2\)	\(0\)	\(2\)	\(2\)	\(2\)	\(2\)	\(4 \)	\(2\)
\(0101\)	\(2\)	\(2\)	\(0\)	\(2\)	\(2\)	\(4\)	\(2\)	\(2\)
\(0110\)	\(2\)	\(2\)	\(2\)	\(0\)	\(4\)	\(2\)	\(2\)	\(2\)
\(1001\)	\(2\)	\(2\)	\(2\)	\(4\)	\(0\)	\(2\)	\(2\)	\(2\)
\(1010\)	\(2\)	\(2\)	\(4\)	\(2\)	\(2\)	\(0\)	\(2\)	\(2\)
\(1100\)	\(2\)	\(4\)	\(2\)	\(2\)	\(2\)	\(2\)	\(0\)	\(2\)
\(1111\)	\(4\)	\(2\)	\(2\)	\(2\)	\(2\)	\(2\)	\(2\)	\(0\)

	\(00000\)	\(00111\)	\(11100\)	\(11011\)
\(00000 \)	\(0\)	\(3\)	\(3\)	\(4\)
\(00111 \)	\(3\)	\(0\)	\(4\)	\(3\)
\(11100 \)	\(3\)	\(4\)	\(0\)	\(3\)
\(11011 \)	\(4\)	\(3\)	\(3\)	\(0\)

Search

Teorema\(8.7\)

Ejemplo\(8.8\)

Ejemplo\(8.9\)

Ejemplo\(8.10\)

Proposición\(8.11\)

Teorema\(8.13\)

Ejemplo\(\PageIndex{1}\)

Ejemplo\(8.2\)

Ejemplo\(8.3\)

Ejemplo\(8.4\)

Decodificación de máxima probabilidad

Teorema\(8.7\)

Ejemplo\(8.8\)

Ejemplo\(8.9\)

Ejemplo\(8.10\)

Proposición\(8.11\)

Teorema\(8.13\)

Ejemplo\(\PageIndex{1}\)

Nota Histórica