12.1: Grupos de Matriz

Algunos hechos del álgebra lineal

Antes de estudiar los grupos matriciales, debemos recordar algunos hechos básicos del álgebra lineal. Una de las ideas más fundamentales del álgebra lineal es la de una transformación lineal. Una transformación lineal o mapa lineal\(T : {\mathbb R}^n \rightarrow {\mathbb R}^m\) es un mapa que conserva la adición de vectores y la multiplicación escalar; es decir, para vectores\({\mathbf x}\)\({\mathbb R}^n\) y\({\mathbf y}\) en y un escalar\(\alpha \in {\mathbb R}\text{,}\)

\ begin {align*} T ({\ mathbf x} + {\ mathbf y}) & = T ({\ mathbf x}) T ({\ mathbf y})\\ T (\ alpha {\ mathbf y}) & =\ alpha T ({\ mathbf y})\ text {.} \ end {alinear*}

Una\(m \times n\) matriz con entradas en\({\mathbb R}\) representa una transformación lineal de\({\mathbb R}^n\) a\({\mathbb R}^m\text{.}\) Si escribimos vectores\({\mathbf x} = (x_1, \ldots, x_n)^{t}\) y\({\mathbf y} = (y_1, \ldots, y_n)^{t}\) en\({\mathbb R}^n\) como matrices de columna, entonces una\(m \times n\) matriz

\[ A = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix} \nonumber \]

mapea los vectores\({\mathbb R}^m\) linealmente por multiplicación matricial. Observe que si\(\alpha\) es un número real,

\[ A({\mathbf x} + {\mathbf y} ) = A {\mathbf x }+ A {\mathbf y} \qquad \text{and} \qquad \alpha A {\mathbf x} = A ( \alpha {\mathbf x})\text{,} \nonumber \]

donde

\[ {\mathbf x} = \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix}\text{.} \nonumber \]

A menudo abreviaremos la matriz\(A\) escribiendo\((a_{ij})\text{.}\)

Por el contrario, si\(T : {\mathbb R}^n \rightarrow {\mathbb R}^m\) es un mapa lineal, podemos asociar una matriz\(A\) con\(T\) considerando lo que\(T\) hace a los vectores

\ begin {align*} {\ mathbf e} _1 & = (1, 0,\ ldots, 0) ^ {t}\\ {\ mathbf e} _2 & = (0, 1,\ ldots, 0) ^ {t}\\ &\ vdots &\\ {\ mathbf e} _n & = (0, 0,\ ldots, 1) ^ {t}\ text {.} \ end {alinear*}

Podemos escribir cualquier vector\({\mathbf x} = (x_1, \ldots, x_n)^{t}\) como

\[ x_1 {\mathbf e}_1 + x_2 {\mathbf e}_2 + \cdots + x_n {\mathbf e}_n\text{.} \nonumber \]

En consecuencia, si

\ begin {alinear*} T ({\ mathbf e} _1) & = (a_ {11}, a_ {21},\ ldots, a_ {m1}) ^ {t},\\ T ({\ mathbf e} _2) & = (a_ {12}, a_ {22},\ ldots, a_ {m2}) ^ {t},\\ & vpuntos &\\ T ({\ mathbf e} _n) & = (a_ {1n}, a_ {2n},\ ldots, a_ {mn}) ^ {t}\ texto {,}\ final {alinear*}

entonces

\ begin {align*} T ({\ mathbf x}) & = T (x_1 {\ mathbf e} _1 + x_2 {\ mathbf e} _2 +\ cdots + x_n {\ mathbf e} _n)\\ & = x_1 T ({\ mathbf e} _1) + x_2 T ({\ mathbf e} _2) +\ cdots + _n T ({\ mathbf e} _n)\\ & =\ izquierda (\ suma_ {k=1} ^ {n} a_ {1k} x_k,\ ldots,\ suma_ {k=1} ^ {n} a_ {mk} x_k\ derecha) ^ {t}\\ & = A {\ mathbf x}\ texto { .} \ end {alinear*}

Ejemplo\(12.1\)

Si dejamos\(T : {\mathbb R}^2 \rightarrow {\mathbb R}^2\) ser el mapa dado por

\[ T(x_1, x_2) = (2 x_1 + 5 x_2, - 4 x_1 + 3 x_2)\text{,} \nonumber \]

los axiomas que\(T\) deben satisfacer para ser una transformación lineal son fácilmente verificados.

Solución

Los vectores de columna\(T {\mathbf e}_1 = (2, -4)^{t}\) y nos\(T {\mathbf e}_2 = (5,3)^{t}\) dicen que\(T\) viene dada por la matriz

\[ A = \begin{pmatrix} 2 & 5 \\ -4 & 3 \end{pmatrix}\text{.} \nonumber \]

Como nos interesan los grupos de matrices, necesitamos saber qué matrices tienen inversos multiplicativos. Recordemos que una\(n \times n\) matriz\(A\) es invertible exactamente cuando existe otra matriz\(A^{-1}\) tal que\(A A^{-1} = A^{-1} A = I\text{,}\) donde

\[ I = \begin{pmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{pmatrix} \nonumber \]

es la matriz\(n \times n\) de identidad. A partir del álgebra lineal sabemos que\(A\) es invertible si y sólo si el determinante de\(A\) es distinto de cero. A veces se dice que una matriz invertible es no singular.

Ejemplo\(12.2\)

Si\(A\) es la matriz

\[ \begin{pmatrix} 2 & 1 \\ 5 & 3 \end{pmatrix}\text{,} \nonumber \]

entonces la inversa de\(A\) es

Solución

\[ A^{-1} = \begin{pmatrix} 3 & -1 \\ -5 & 2 \end{pmatrix}\text{.} \nonumber \]

Se nos garantiza que\(A^{-1}\) existe, ya que\(\det(A) = 2 \cdot 3 - 5 \cdot 1 = 1\) es distinto de cero.

Algunos otros datos sobre determinantes también resultarán útiles en el transcurso de este capítulo. Dejar\(A\) y\(B\) ser\(n \times n\) matrices. Del álgebra lineal tenemos las siguientes propiedades de determinantes.

• El determinante es un homomorfismo dentro del grupo multiplicativo de números reales; es decir,\(\det( A B) = (\det A )(\det B)\text{.}\)
• Si\(A\) es una matriz invertible, entonces\(\det(A^{-1}) = 1 / \det A\text{.}\)
• Si definimos la transposición de una matriz\(A = (a_{ij})\) para ser\(A^{t} = (a_{ji})\text{,}\) entonces\(\det(A^{t}) = \det A\text{.}\)
• Dejar\(T\) ser la transformación lineal asociada a una\(n \times n\) matriz\(A\text{.}\) Luego\(T\) multiplica los volúmenes por un factor de\(|\det A|\text{.}\) En el caso de\({\mathbb R}^2\text{,}\) esto significa que\(T\) multiplica áreas por\(|\det A|\text{.}\)

Los mapas lineales, matrices y determinantes están cubiertos en cualquier texto elemental de álgebra lineal; sin embargo, si no ha tenido un curso en álgebra lineal, es un proceso sencillo verificar estas propiedades directamente para\(2 \times 2\) matrices, el caso del que más nos preocupa.

Los grupos lineales generales y especiales

El conjunto de todas las matrices\(n \times n\) invertibles forma un grupo llamado grupo lineal general. Denotaremos este grupo por\(GL_n({\mathbb R})\text{.}\) El grupo lineal general tiene varios subgrupos importantes. Las propiedades multiplicativas del determinante implican que el conjunto de matrices con determinante uno es un subgrupo del grupo lineal general. Dicho de otra manera, supongamos que\(\det(A) =1\)\(\det(AB) = \det(A) \det (B) = 1\) y\(\det(B) = 1\text{.}\) Entonces y\(\det(A^{-1}) = 1 / \det A = 1\text{.}\) Este subgrupo se llama el grupo lineal especial y se denota por\(SL_n({\mathbb R})\text{.}\)

Ejemplo\(12.3\)

Dada una\(2 \times 2\) matriz

\[ A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}\text{,} \nonumber \]

el determinante de\(A\) es\(ad-bc\text{.}\) El grupo\(GL_2({\mathbb R})\) consiste en aquellas matrices en las que\(ad-bc \neq 0\text{.}\) La inversa de\(A\) es

\[ A^{-1} = \frac{1}{ad-bc} \begin{pmatrix} d & -b \\ -c & a \end{pmatrix}\text{.} \nonumber \]

Solución

Si\(A\) está en\(SL_2({\mathbb R})\text{,}\) entonces

\[ A^{-1} = \begin{pmatrix} d & -b \\ -c & a \end{pmatrix}\text{.} \nonumber \]

Geométricamente,\(SL_2({\mathbb R})\) es el grupo que conserva las áreas de paralelogramos. Let

\[ A = \begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix} \nonumber \]

estar en\(SL_2({\mathbb R})\text{.}\) En Figura\(12.4\), el cuadrado unitario correspondiente a los vectores\({\mathbf x} = (1,0)^{t}\) y\({\mathbf y} = (0,1)^{t}\) es tomado por\(A\) al paralelogramo con lados\((1,0)^{t}\) y es\((1, 1)^{t}\text{;}\) decir,\(A {\mathbf x} = (1,0)^{t}\) y\(A {\mathbf y} = (1, 1)^{t}\text{.}\) Observe que estos dos paralelogramos tienen la misma área.

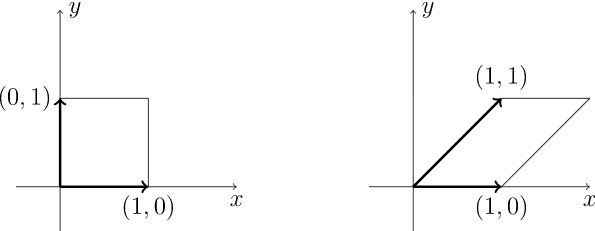
\(Figure \text { } 12.4.\)\(SL_2(\mathbb R)\)actuando sobre el cuadrado de la unidad

El grupo ortogonal\(O(n)\)

Otro subgrupo de\(GL_n({\mathbb R})\) es el grupo ortogonal. Una matriz\(A\) es ortogonal si\(A^{-1} = A^{t}\text{.}\) El grupo ortogonal consiste en el conjunto de todas las matrices ortogonales. Escribimos\(O(n)\) para el grupo\(n \times n\) ortogonal. Dejamos como ejercicio la prueba de que\(O(n)\) es un subgrupo de\(GL_n( {\mathbb R})\text{.}\)

Ejemplo\(12.5\)

Las siguientes matrices son ortogonales:

Solución

\[ \begin{pmatrix} 3/5 & -4/5 \\ 4/5 & 3/5 \end{pmatrix}, \quad \begin{pmatrix} 1/2 & -\sqrt{3}/2 \\ \sqrt{3}/2 & 1/2 \end{pmatrix}, \quad \begin{pmatrix} -1/\sqrt{2} & 0 & 1/ \sqrt{2} \\ 1/\sqrt{6} & -2/\sqrt{6} & 1/\sqrt{6} \\ 1/ \sqrt{3} & 1/ \sqrt{3} & 1/ \sqrt{3} \end{pmatrix}\text{.} \nonumber \]

Hay una forma más geométrica de visualizar el grupo\(O(n)\text{.}\) Las matrices ortogonales son exactamente aquellas matrices que conservan la longitud de los vectores. Podemos definir la longitud de un vector usando el producto interno euclidiano, o producto punto, de dos vectores. El producto interno euclidiano de dos vectores\({\mathbf x}=(x_1, \ldots, x_n)^{t}\) y\({\mathbf y}=(y_1, \ldots, y_n)^{t}\) es

\[ \langle {\mathbf x}, {\mathbf y} \rangle = {\mathbf x}^{t} {\mathbf y} = (x_1, x_2, \ldots, x_n) \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix} = x_1 y_1 + \cdots + x_n y_n\text{.} \nonumber \]

Definimos la longitud de un vector\({\mathbf x}=(x_1, \ldots, x_n)^{t}\) para que sea

\[ \| {\mathbf x} \| = \sqrt{\langle {\mathbf x}, {\mathbf x} \rangle} = \sqrt{x_1^2 + \cdots + x_n^2}\text{.} \nonumber \]

Asociada a la noción de la longitud de un vector está la idea de la distancia entre dos vectores. Definimos la distancia entre dos vectores\({\mathbf x}\) y\({\mathbf y}\) ser\(\| {\mathbf x}-{\mathbf y} \|\text{.}\) Dejamos como ejercicio la prueba de la siguiente proposición sobre las propiedades de los productos internos euclidianos.

Proposición\(12.6\)

Dejar\({\mathbf x}\text{,}\)\({\mathbf y}\text{,}\) y\({\mathbf w}\) ser vectores en\({\mathbb R}^n\) y\(\alpha \in {\mathbb R}\text{.}\) Entonces

1. \(\langle {\mathbf x}, {\mathbf y} \rangle = \langle {\mathbf y}, {\mathbf x} \rangle\text{.}\)
2. \(\langle {\mathbf x}, {\mathbf y} + {\mathbf w} \rangle = \langle {\mathbf x}, {\mathbf y} \rangle + \langle {\mathbf x}, {\mathbf w} \rangle\text{.}\)
3. \(\langle \alpha {\mathbf x}, {\mathbf y} \rangle = \langle {\mathbf x}, \alpha {\mathbf y} \rangle = \alpha \langle {\mathbf x}, {\mathbf y} \rangle\text{.}\)
4. \(\langle {\mathbf x}, {\mathbf x} \rangle \geq 0\)con igualdad exactamente cuando\({\mathbf x} = 0\text{.}\)
5. Si\(\langle {\mathbf x}, {\mathbf y} \rangle = 0\) para todos\({\mathbf x}\) en\({\mathbb R}^n\text{,}\) entonces\({\mathbf y} = 0\text{.}\)

Ejemplo\(12.7\)

El vector\({\mathbf x} =(3,4)^{t}\) tiene longitud También\(\sqrt{3^2 + 4^2} = 5\text{.}\) podemos ver que la matriz ortogonal

\[ A= \begin{pmatrix} 3/5 & -4/5 \\ 4/5 & 3/5 \end{pmatrix} \nonumber \]

conserva la longitud de este vector. El vector\(A{\mathbf x} = (-7/5,24/5)^{t}\) también tiene longitud 5.

Dado que\(\det(A A^{t}) = \det(I) = 1\) y\(\det(A) = \det( A^{t} )\text{,}\) el determinante de cualquier matriz ortogonal es cualquiera\(1\) o\(-1\text{.}\) Considere los vectores de columna

\[ {\mathbf a}_j = \begin{pmatrix} a_{1j} \\ a_{2j} \\ \vdots \\ a_{nj} \end{pmatrix} \nonumber \]

de la matriz ortogonal\(A= (a_{ij})\text{.}\) Desde\(AA^{t} = I\text{,}\)\(\langle {\mathbf a}_r, {\mathbf a}_s \rangle = \delta_{rs}\text{,}\) donde

\[ \delta_{rs} = \begin{cases} 1 & r = s \\ 0 & r \neq s \end{cases} \nonumber \]

es el delta de Kronecker. En consecuencia, los vectores de columna de una matriz ortogonal tienen todos longitud 1; y el producto interno euclidiano de vectores de columna distintos es cero. Cualquier conjunto de vectores que satisfaga estas propiedades se denomina conjunto ortonormal. Por el contrario, dada una\(n \times n\) matriz\(A\) cuyas columnas forman un conjunto ortonormal, se deduce que\(A^{-1} = A^{t}\text{.}\)

Decimos que una matriz\(A\) es conservadora a distancia, conservadora de longitud o conservadora de producto interna cuando\(\| A{\mathbf x}- A{\mathbf y} \| =\| {\mathbf x}- {\mathbf y} \|\text{,}\)\(\| A{\mathbf x} \| =\| {\mathbf x} \|\text{,}\) o\(\langle A{\mathbf x}, A{\mathbf y} \rangle = \langle {\mathbf x},{\mathbf y} \rangle\text{,}\) respectivamente. El siguiente teorema, que caracteriza al grupo ortogonal, dice que estas nociones son las mismas.

Teorema\(12.8\)

\(A\)Déjese ser una\(n \times n\) matriz. Las siguientes declaraciones son equivalentes.

1. Las columnas de la matriz\(A\) forman un conjunto ortonormal.
2. \(A^{-1} = A^{t}\text{.}\)
3. Para vectores\({\mathbf x}\) y\({\mathbf y}\text{,}\)\(\langle A{\mathbf x}, A {\mathbf y} \rangle = \langle {\mathbf x}, {\mathbf y} \rangle\text{.}\)
4. Para vectores\({\mathbf x}\) y\({\mathbf y}\text{,}\)\(\| A{\mathbf x}- A{\mathbf y} \| = \| {\mathbf x}- {\mathbf y} \|\text{.}\)
5. Para cualquier vector\({\mathbf x}\text{,}\)\(\| A{\mathbf x} \| = \| {\mathbf x}\|\text{.}\)

Prueba

Ya hemos demostrado que (1) y (2) son equivalentes.

\((2) \Rightarrow (3)\text{.}\)

\ begin {align*}\ langle A {\ mathbf x}, A {\ mathbf y}\ rangle & = (A {\ mathbf x}) ^ {t} A {\ mathbf y}\\ & = {\ mathbf x} ^ {t} A^ {t} A {\ mathbf y}\\ & = {\ mathbf x} ^ {t} {\ y mathbf}\\ & =\ langle {\ mathbf x}, {\ mathbf y}\ rangle\ texto {.} \ end {alinear*}

\((3) \Rightarrow (2)\text{.}\)Desde

\ begin {align*}\ langle {\ mathbf x}, {\ mathbf x}\ rangle & =\ langle A {\ mathbf x}, A {\ mathbf x}\ rangle\\ & = {\ mathbf x} ^ {t} A^ {t} A {\ mathbf x}\\ & =\ langle {\ mathbf x}, A^ {t} A {\ mathbf x}\ rangle\ text {,}\ end {align*}

sabemos que\(\langle {\mathbf x}, (A^{t} A - I){\mathbf x} \rangle = 0\) para todos Por\({\mathbf x}\text{.}\) lo tanto,\(A^{t} A -I = 0\) o\(A^{-1} = A^{t}\text{.}\)

\((3) \Rightarrow (4)\text{.}\)Si\(A\) es la preservación interna del producto, entonces\(A\) es la preservación a distancia, ya que

\ begin {align*}\ | A {\ mathbf x} - A {\ mathbf y}\ |^2 & =\ | A ({\ mathbf x} - {\ mathbf y})\ |^2\\ & =\ langle A ({\ mathbf x} - {\ mathbf y}), A ({\ mathbf x} - {\ mathbf y})\ rangle\\ & =\ langle {\ mathbf x} - {\ mathbf y}, {\ mathbf x} - {\ mathbf y}\ rangle\\ & =\ | {\ mathbf x} - {\ mathbf y}\ |^2\ text {.} \ end {alinear*}

\((4) \Rightarrow (5)\text{.}\)Si\(A\) es preservar la distancia, entonces\(A\) es preservar la longitud. Dejando\({\mathbf y} = 0\text{,}\) que tengamos

\[ \| A{\mathbf x}\| = \| A{\mathbf x}- A{\mathbf y} \| = \| {\mathbf x}- {\mathbf y} \| = \| {\mathbf x} \|\text{.} \nonumber \]

\((5) \Rightarrow (3)\text{.}\)Utilizamos la siguiente identidad para mostrar que preservar la longitud implica preservar el producto interno:

\[ \langle {\mathbf x}, {\mathbf y} \rangle = \frac{1}{2} \left[ \|{\mathbf x} +{\mathbf y}\|^2 - \|{\mathbf x}\|^2 - \|{\mathbf y}\|^2 \right]\text{.} \nonumber \]

Observe que

\ begin {align*}\ langle A {\ mathbf x}, A {\ mathbf y}\ rangle & =\ frac {1} {2}\ left [\ |A {\ mathbf x} + A {\ mathbf y}\ |^2 -\ |A {\ mathbf x}\ |^2 -\ |A {\ mathbf y}\ |^2\ derecha]\\ & =\ frac {1} {2}\ left [\ |A ({\ mathbf x} + {\ mathbf y})\ |^2 -\ |A {\ mathbf x}\ |^2 -\ |A {\ mathbf y}\ |^2\ derecha]\\ & =\ frac {1} {2}\ left [\ | {\ mathbf x} + {\ mathbf y}\ |^2 -\ | {\ mathbf x}\ |^2 -\ | {\ mathbf y}\ |^2\ derecha]\\ & =\ langle {\ mathbf x}, {\ mathbf y}\ rangle\ texto {.} \ end {alinear*}

\(Figure \text { } 12.9.\)\(O(2)\)actuando sobre\(\mathbb R^2\)

Ejemplo 12.10

Examinemos el grupo ortogonal\({\mathbb R}^2\) un poco más de cerca. Un elemento\(A \in O(2)\) está determinado por su acción sobre\({\mathbf e}_1 = (1, 0)^{t}\) y\({\mathbf e}_2 = (0, 1)^{t}\text{.}\) Si\(A{\mathbf e}_1 = (a,b)^{t}\text{,}\) entonces\(a^2 + b^2 = 1\text{,}\) ya que la longitud de un vector debe conservarse cuando se multiplica por\(A\text{.}\) Desde la multiplicación de un elemento de\(O(2)\) conserva longitud y ortogonalidad,\(A{\mathbf e}_2 = \pm(-b, a)^{t}\text{.}\) Si elegimos \(A{\mathbf e}_2 = (-b, a)^{t}\text{,}\)entonces

\[ A = \begin{pmatrix} a & -b \\ b & a \end{pmatrix} = \begin{pmatrix} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{pmatrix}, \nonumber \]

donde\(0 \leq \theta \lt 2 \pi\text{.}\) La matriz\(A\) gira un vector en\(\mathbb R^2\) sentido antihorario alrededor del origen en un ángulo de\(\theta\) (Figura 12.9).

Si elegimos\(A{\mathbf e}_2 = (b, -a)^{t}\text{,}\) entonces obtenemos la matriz

\[ B = \begin{pmatrix} a & b \\ b & -a \end{pmatrix} = \begin{pmatrix} \cos \theta & \sin \theta \\ \sin \theta & -\cos \theta \end{pmatrix}. \nonumber \]

Aquí,\(\det B = -1\) y

\[ B^2 = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}. \nonumber \]

Una reflexión sobre el eje horizontal viene dada por la matriz

\[ C = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}, \nonumber \]

y\(B = AC\) (véase la Figura 12.9). Así, una reflexión alrededor de una línea\(\ell\) es simplemente una reflexión alrededor del eje horizontal seguida de una rotación.

Dos de los otros grupos matriciales o relacionados con la matriz que consideraremos son el grupo ortogonal especial y el grupo de movimientos euclidianos. El grupo ortogonal especial,\(SO(n)\text{,}\) es solo la intersección de\(O(n)\) y es\(SL_n({\mathbb R})\text{;}\) decir, esos elementos\(O(n)\) con uno determinante. El grupo euclidiano, se\(E(n)\text{,}\) puede escribir como pares ordenados\((A, {\mathbf x})\text{,}\) donde\(A\) está adentro\(O(n)\) y\({\mathbf x}\) está en\({\mathbb R}^n\text{.}\) Definimos multiplicación por

\[ (A, {\mathbf x}) (B, {\mathbf y}) = (AB, A {\mathbf y} +{\mathbf x})\text{.} \nonumber \]

La identidad del grupo es\((I,{\mathbf 0})\text{;}\) la inversa de\((A, {\mathbf x})\) es\((A^{-1}, -A^{-1} {\mathbf x})\text{.}\) En el Ejercicio 12.4.6, se le pide que compruebe que efectivamente\(E(n)\) es un grupo bajo esta operación.

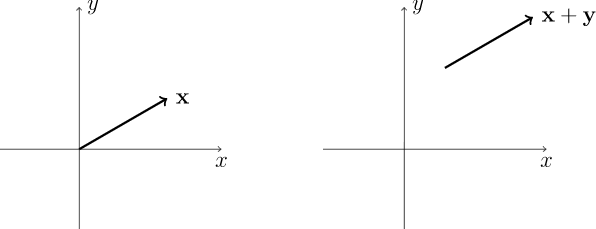
\(Figure \text { } 12.11.\)Traducciones en\(\mathbb R^2\)