12.2: Simetría
- Page ID
- 111144
Una isometría o movimiento rígido en\({\mathbb R}^n\) es una función de preservación de distancia\(f\) desde\({\mathbb R}^n\) hasta\({\mathbb R}^n\text{.}\) Esto significa que\(f\) debe satisfacer
para todos\({\mathbf x}, {\mathbf y} \in {\mathbb R}^n\text{.}\) No es difícil demostrar que\(f\) debe ser un mapa uno a uno. Por teorema\(12.8\), cualquier elemento en\(O(n)\) es una isometría en\({\mathbb R}^n\text{;}\) sin embargo,\(O(n)\) no incluye todas las isometrías posibles en La\({\mathbb R}^n\text{.}\) traducción por un vector también\({\mathbf x}\text{,}\)\(T_{\mathbf y}({\mathbf x}) = {\mathbf x} + {\mathbf y}\) es una isometría (Figura\(12.11\)); sin embargo,\(T\) no puede estar en\(O(n)\) ya que no es un mapa lineal.
Nos interesan mayormente las isometrías\({\mathbb R}^2\text{.}\) en De hecho, las únicas isometrías en\({\mathbb R}^2\) son rotaciones y reflexiones sobre el origen, traducciones, y combinaciones de las dos. Por ejemplo, una reflexión de deslizamiento es una traslación seguida de una reflexión (Figura 12.12). En\({\mathbb R}^n\) todas las isometrías se dan de la misma manera. La prueba es muy fácil de generalizar.
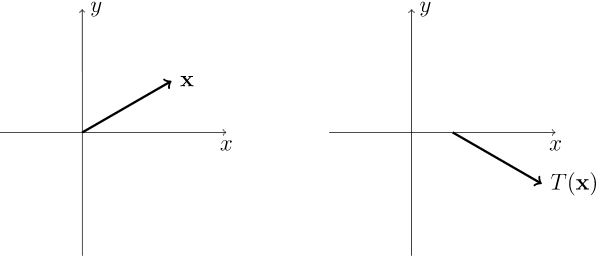
\(Figure \text { } 12.12.\)Reflexiones de deslizamiento
Lema\(12.13\)
Una isometría\(f\) que fija el origen en\({\mathbb R}^2\) es una transformación lineal. En particular,\(f\) viene dado por un elemento en\(O(2)\text{.}\)
- Prueba
-
Dejar\(f\) ser una isometría en la\({\mathbb R}^2\) fijación del origen. Primero mostraremos que\(f\) conserva los productos internos. Dado que,\(f(0) = 0\text{,}\)\(\| f({\mathbf x})\| = \| {\mathbf x} \|\text{;}\) por tanto,
\ begin {align*}\ | {\ mathbf x}\ |^2 - 2\ langle f ({\ mathbf x}), f ({\ mathbf y})\ rangle +\ | {\ mathbf y}\ |^2 & =\ | f ({\ mathbf x})\ |^2 - 2\ langle f ({\ mathbf x}), f ({\ mathbf x}), f ({\ mathbf x})\ mathbf y})\ rangle +\ | f ({\ mathbf y})\ |^2\\ & =\ langle f ({\ mathbf x}) - f ({\ mathbf y}), f ({\ mathbf x}) - f ({\ mathbf y})\ rangle\\ & =\ | f ({\ mathbf x}) - f ({\ mathbf y})\ |^2\\ & =\ | {\ mathbf x} - {\ mathbf y}\ |^2\ & =\ langle {\ mathbf x} - {\ mathbf y}, {\ mathbf x} - {\ mathbf y}\ rangle\\ & =\ | {\ mathbf x}\ |^2 - 2\ langle {\ mathbf x}, {\ mathbf y}\ rangle +\ | {\ mathbf y}\ |^2\ text {.} \ end {align*}En consecuencia,
\[ \langle f({\mathbf x}), f({\mathbf y}) \rangle = \langle {\mathbf x}, {\mathbf y} \rangle\text{.} \nonumber \]Ahora vamos\({\mathbf e}_1\) y\({\mathbf e_2}\) ser\((1, 0)^^{t}\) y\((0, 1)^^{t}\text{,}\) respectivamente. Si
\[ {\mathbf x} = (x_1, x_2) = x_1 {\mathbf e}_1 + x_2 {\mathbf e}_2\text{,} \nonumber \]entonces
\[ f({\mathbf x}) = \langle f({\mathbf x}), f({\mathbf e}_1) \rangle f({\mathbf e}_1) + \langle f({\mathbf x}), f({\mathbf e}_2) \rangle f({\mathbf e}_2) = x_1 f({\mathbf e}_1)+x_2 f({\mathbf e}_2)\text{.} \nonumber \]La linealidad de\(f\) fácilmente sigue.
Para cualquier isometría arbitraria,\(f\text{,}\)\(T_{\mathbf x} f\) se fijará el origen de algún vector\({\mathbf x}\) en\({\mathbb R}^2\text{;}\) por lo tanto,\(T_{\mathbf x} f({\mathbf y}) = A {\mathbf y}\) para alguna matriz en\(A \in O(2)\text{.}\) consecuencia,\(f({\mathbf y}) = A {\mathbf y} + {\mathbf x}\text{.}\) dadas las isometrías
su composición es
Este último cómputo nos permite identificar el grupo de isometrías\({\mathbb R}^2\) con\(E(2)\text{.}\)
Teorema\(12.14\)
El grupo de isometrías\({\mathbb R}^2\) es el grupo euclidiano,\(E(2)\text{.}\)
Un grupo de simetría en\({\mathbb R}^n\) es un subgrupo del grupo de isometrías sobre el\({\mathbb R}^n\) que fija un conjunto de puntos\(X \subset {\mathbb R}^n\text{.}\) Es importante darse cuenta de que el grupo de simetría de\(X\) depende \({\mathbb R}^n\)tanto de como de\(X\text{.}\) Por ejemplo, el grupo de simetría del origen en\({\mathbb R}^1\) es\({\mathbb Z}_2\text{,}\) pero el grupo de simetría del origen en\({\mathbb R}^2\) es\(O(2)\text{.}\)
Teorema\(12.15\)
Los únicos grupos de simetría finita en\({\mathbb R}^2\) son\({\mathbb Z}_n\) y\(D_n\text{.}\)
- Prueba
-
Simplemente necesitamos encontrar todos los subgrupos finitos de\(E(2)\text{.}\) Cualquier grupo\(G\) de simetría finita\(G\) en\({\mathbb R}^2\) debe fijar el origen y debe ser un subgrupo finito de\(O(2)\text{,}\) ya que las traducciones y reflexiones de deslizamiento tienen orden infinito. Por el Ejemplo 12.10, los elementos en\(O(2)\) son rotaciones de la forma
\[ R_{\theta} = \begin{pmatrix} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{pmatrix} \nonumber \]o reflexiones de la forma
\[ T_{\phi} = \begin{pmatrix} \cos \phi & - \sin \phi \\ \sin \phi & \cos \phi \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} = \begin{pmatrix} \cos \phi & \sin \phi \\ \sin \phi & - \cos \phi \end{pmatrix}\text{.} \nonumber \]Observe eso\(\det(R_{\theta})=1\text{,}\)\(\det(T_{\phi})=-1\text{,}\) y\(T_{\phi}^2=I\text{.}\) Podemos dividir la prueba hasta en dos casos. En el primer caso, todos los elementos en\(G\) tienen uno determinante. En el segundo caso, existe al menos un elemento\(G\) con determinante\(-1\text{.}\)
Caso 1.
El determinante de cada elemento en\(G\) es uno. En este caso cada elemento en\(G\) debe ser una rotación. Ya que\(G\) es finito, hay un ángulo más pequeño, digamos\(\theta_0\text{,}\) tal que el elemento correspondiente\(R_{\theta_0}\) es la rotación más pequeña en la dirección positiva. Afirmamos que\(R_{\theta_0}\) genera\(G\text{.}\) Si no, entonces para algún entero positivo\(n\) hay un ángulo\(\theta_1\) entre\(n \theta_0\) y\((n+1) \theta_0\text{.}\) Si es así, entonces\((n+1) \theta_0 - \theta_1\) corresponde a una rotación menor\(\theta_0\text{,}\) que la que contradice la minimalidad de\(\theta_0\text{.}\)
Caso 2.
El grupo\(G\) contiene una reflexión\(T\text{.}\) El núcleo del homomorfismo\(\phi : G \rightarrow \{-1, 1\}\) dado por\(A \mapsto \det(A)\) consiste en elementos cuyo determinante es 1. Por lo tanto,\(|G/ \ker \phi|=2\text{.}\) sabemos que el kernel es cíclico por el primer caso y es un subgrupo\(G\) de, digamos, orden\(n\text{.}\) De ahí,\(|G| = 2n\text{.}\) Los elementos de\(G\) son
\[ R_{\theta}, \ldots, R_{\theta}^{n-1}, TR_{\theta}, \ldots, TR_{\theta}^{n-1}\text{.} \nonumber \]Estos elementos satisfacen la relación
\[ TR_{\theta}T = R_{\theta}^{-1}\text{.} \nonumber \]En consecuencia,\(G\) debe ser isomórfico para\(D_n\) en este caso.
Los grupos de papel tapiz
Supongamos que deseamos estudiar patrones de papel tapiz en el plano o cristales en tres dimensiones. Los patrones de papel tapiz son simplemente patrones repetidos en el plano (Figura\(12.16\)).
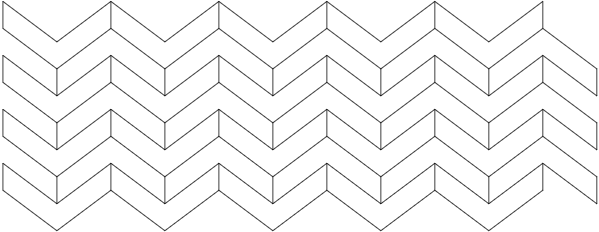
\(Figure \text { } 12.16.\)Un patrón de papel tapiz en\(\mathbb R^2\)
Los análogos de los patrones de papel tapiz en\({\mathbb R}^3\) son los cristales, que podemos pensar como patrones repetitivos de moléculas en tres dimensiones (Figura\(12.17\)). El equivalente matemático de un fondo de pantalla o patrón de cristal se llama celosía.
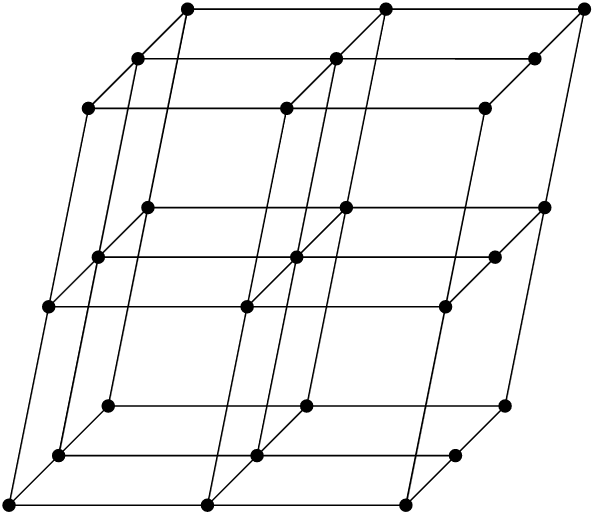
\(Figure \text { } 12.17.\)Una estructura cristalina en\(\mathbb R^3\)
Examinemos los patrones de papel tapiz en el avión un poco más de cerca. Supongamos que\({\mathbf x}\) y\({\mathbf y}\) son vectores linealmente independientes en\({\mathbb R}^2\text{;}\) esto es, un vector no puede ser un múltiplo escalar del otro. Una celosía de\({\mathbf x}\) y\({\mathbf y}\) es el conjunto de todas las combinaciones lineales\(m {\mathbf x} + n {\mathbf y}\text{,}\) donde\(m\) y\(n\) son números enteros. Los vectores\({\mathbf x}\) y\({\mathbf y}\) se dice que son una base para la celosía.
Observe que una celosía puede tener varias bases. Por ejemplo, los vectores\((1,1)^^{t}\) y\((2,0)^^{t}\) tienen la misma celosía que los vectores\((-1, 1)^^{t}\) y\((-1, -1)^^{t}\) (Figura\(12.18\)). Sin embargo, cualquier celosía está completamente determinada por una base. Dadas dos bases para la misma celosía, digamos\(\{ {\mathbf x}_1, {\mathbf x}_2 \}\) y\(\{ {\mathbf y}_1, {\mathbf y}_2 \}\text{,}\) podemos escribir
donde\(\alpha_1\text{,}\)\(\alpha_2\text{,}\)\(\beta_1\text{,}\) y\(\beta_2\) son enteros. La matriz correspondiente a esta transformación es
Si queremos dar\({\mathbf x}_1\) y\({\mathbf x}_2\) en términos de\({\mathbf y}_1\) y sólo\({\mathbf y}_2\text{,}\) necesitamos calcular es\(U^{-1}\text{;}\) decir,
Dado que\(U\) tiene entradas enteras, también\(U^{-1}\) debe tener entradas enteras; de ahí los determinantes de ambos\(U\) y\(U^{-1}\) deben ser enteros. Porque\(U U^{-1} = I\text{,}\)
en consecuencia,\(\det(U) = \pm 1\text{.}\) una matriz con entradas determinantes\(\pm 1\) y enteros se llama unimodular. Por ejemplo, la matriz
es unimodular. Debe quedar claro que hay una longitud mínima para los vectores en una celosía.
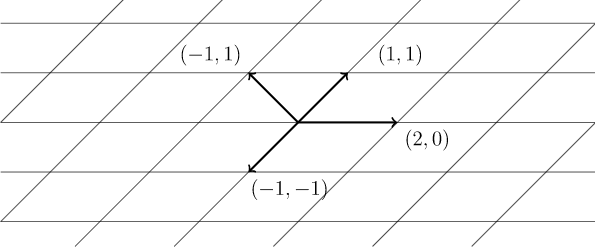
\(Figure \text { } 12.18.\)Una celosía en\(\mathbb R^2\)
Podemos clasificar las celosías mediante el estudio de sus grupos de simetría. El grupo de simetría de una celosía es el subgrupo de\(E(2)\) que mapea la celosía a sí misma. Consideramos que dos celosías son equivalentes si tienen el mismo grupo de simetría.\({\mathbb R}^2\) De igual manera, la clasificación de los cristales en\({\mathbb R}^3\) se logra asociando un grupo de simetría, llamado grupo espacial, con cada tipo de cristal. Dos celosías se consideran diferentes si sus grupos espaciales no son los mismos. La pregunta natural que ahora se plantea es cuántos grupos espaciales existen.
Un grupo espacial se compone de dos partes: un subgrupo de traducción y un punto. El subgrupo de traducción es un subgrupo abeliano infinito del grupo espacial formado por las simetrías traslacionales del cristal; el grupo de puntos es un grupo finito que consiste en rotaciones y reflexiones del cristal alrededor de un punto. Más específicamente, un grupo espacial es un subgrupo de\(G \subset E(2)\) cuyas traducciones son un conjunto de la forma\(\{ (I, t) : t \in L \}\text{,}\) donde\(L\) es una celosía. Los grupos espaciales son, por supuesto, infinitos. Usando argumentos geométricos, podemos probar el siguiente teorema (ver [5] o [6]).
Teorema\(12.19\)
Cada grupo de traducción en\({\mathbb R}^2\) es isomórfico a\ ({\ mathbb Z}\ times {\ mathbb Z}\ text { . }\
El grupo de puntos de\(G\) es\(G_0 = \{A : (A,b) \in G \text{ for some } b \}\text{.}\) En particular,\(G_0\) debe ser un subgrupo de\(O(2)\text{.}\) Supongamos que\({\mathbf x}\) es un vector en una celosía\(L\) con grupo de espacio grupo de\(G\text{,}\) traducción\(H\text{,}\) y grupo de puntos\(G_0\text{.}\) Para cualquier elemento\((A, {\mathbf y})\) en\(G\text{,}\)
por lo tanto,\((I, A {\mathbf x})\) está en el grupo de traducción de\(G\text{.}\) Más específicamente,\(A {\mathbf x}\) debe estar en la celosía\(L\text{.}\) Es importante señalar que no\(G_0\) suele ser un subgrupo del grupo espacial\(G\text{;}\) sin embargo, si\(T\) es el subgrupo de traducción de\(G\text{,}\) entonces\(G/T \cong G_0\text{.}\) El prueba del siguiente teorema se puede encontrar en [2], [5], o [6].
Teorema\(12.20\)
El grupo de puntos en los grupos de fondo de pantalla es isomorfo a\({\mathbb Z}_n\) o\(D_n\text{,}\) donde\(n = 1, 2, 3, 4, 6\text{.}\)
Para responder a la pregunta de cómo se pueden combinar los grupos de puntos y los grupos de traducción, debemos mirar los diferentes tipos de celosías. Las celosías se pueden clasificar por la estructura de una sola celda de celosía. Las posibles formas celulares son paralelogramo, rectangular, cuadrada, rómbica y hexagonal (Figura 12.21). Los grupos de fondo de pantalla ahora se pueden clasificar de acuerdo con los tipos de reflejos que ocurren en cada grupo: estos son normalmente reflejos, reflejos de deslizamiento, ambos, o ninguno.
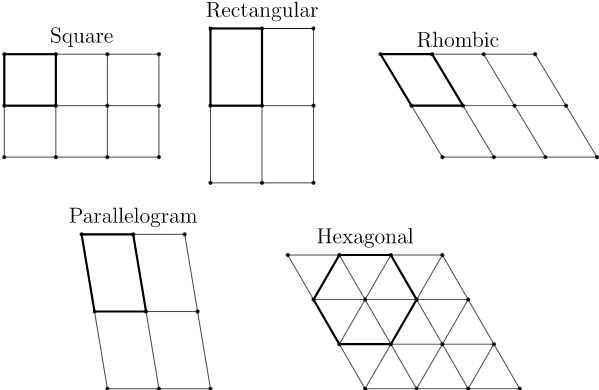
\(Figure \text { } 12.21.\)Tipos de celosías en\(\mathbb R^2\)
| Grupos de Notación y Espacio | Grupo de puntos | Tipo de celosía | ¿Reflexiones o reflexiones de deslizamiento? |
|---|---|---|---|
| p1 | \({\mathbb Z}_1\) | paralelogramo | ninguno |
| p2 | \({\mathbb Z}_2\) | paralelogramo | ninguno |
| p3 | \({\mathbb Z}_3\) | hexagonal | ninguno |
| p4 | \({\mathbb Z}_4\) | cuadrado | ninguno |
| p6 | \({\mathbb Z}_6\) | hexagonal | ninguno |
| pm | \(D_1\) | rectangular | reflexiones |
| pg | \(D_1\) | rectangular | reflejos de deslizamiento |
| cm | \(D_1\) | rómbico | ambos |
| pmm | \(D_2\) | rectangular | reflexiones |
| pmg | \(D_2\) | rectangular | reflejos de deslizamiento |
| pgg | \(D_2\) | rectangular | ambos |
| c2mm | \(D_2\) | rómbico | ambos |
| p3m1, p31m | \(D_3\) | hexagonal | ambos |
| p4m, p4g | \(D_4\) | cuadrado | ambos |
| p6m | \(D_6\) | hexagonal | ambos |
Teorema\(12.23\)
Hay exactamente 17 grupos de papel tapiz.
Los 17 grupos de papel tapiz se enumeran en la Tabla\(12.22\). Los grupos p3m1 y p31m se pueden distinguir por si todos sus centros triplicados se encuentran o no en los ejes de reflexión: los de p3m1 deben, mientras que los de p31m pueden no. De manera similar, los cuatro centros de p4m deben estar sobre los ejes de reflexión mientras que los de p4g no necesitan (Figura\(12.24\)). La prueba completa de este teorema se puede encontrar en varias de las referencias al final de este capítulo, incluyendo [5], [6], [10] y [11].
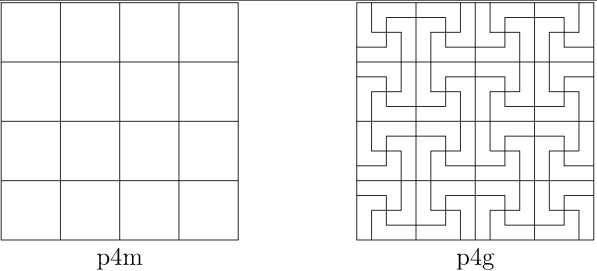
\(Figure \text { } 12.24.\)Los grupos de papel tapiz p4m y p4g
Nota Histórica
Los grupos de simetría han intrigado a los matemáticos desde hace mucho tiempo. Leonardo da Vinci fue probablemente la primera persona en conocer todos los grupos puntuales. En el Congreso Internacional de Matemáticos en 1900, David Hilbert dio una ahora famosa dirección esbozando 23 problemas para guiar las matemáticas en el siglo XX. El decimoctavo problema de Hilbert se preguntaba si los grupos cristalográficos en\(n\) dimensiones eran siempre finitos o no. En 1910, L. Bieberbach demostró que los grupos cristalográficos son finitos en todas las dimensiones. Descubrir cuántos de estos grupos hay en cada dimensión es otro asunto. En\({\mathbb R}^3\) hay 230 grupos espaciales diferentes; en\({\mathbb R}^4\) hay 4783. Nadie ha podido calcular el número de grupos espaciales para\({\mathbb R}^5\) y más allá. Es interesante observar que los grupos cristalográficos se encontraron matemáticamente para\({\mathbb R}^3\) antes de que los 230 tipos diferentes de cristales fueran descubiertos realmente en la naturaleza.


