14.5: Ejercicios

1

Los ejemplos\(14.1–14.5\) en la primera sección describen cada uno una acción de un grupo\(G\) sobre un conjunto\(X\text{,}\) que dará lugar a la relación de equivalencia definida por\(G\) -equivalencia. Para cada ejemplo, computar las clases de equivalencia de la relación de equivalencia, las clases de equivalencia\(G\) -.

2

Calcular todos\(X_g\) y todos\(G_x\) para cada uno de los siguientes grupos de permutación.

1. \(X= \{1, 2, 3\}\text{,}\)\(G=S_3=\{(1), (1 \, 2), (1 \, 3), (2 \, 3), (1 \, 2 \, 3), (1 \, 3 \, 2) \}\)
2. \(X = \{1, 2, 3, 4, 5, 6\}\text{,}\)\(G = \{(1), (1 \, 2), (3 \, 4 \, 5), (3 \, 5 \, 4), (1 \, 2)(3 \, 4 \, 5), (1 \, 2)(3 \, 5 \, 4) \}\)

3

Calcular las clases de\(G\) -equivalencia de\(X\) para cada uno de los\(G\) -conjuntos en Ejercicio\(14.5.2\). Para cada uno\(x \in X\) verificar que\(|G|=|{\mathcal O}_x| \cdot |G_x|\text{.}\)

4

Dejar\(G\) ser el grupo aditivo de los números reales. Que la acción de\(\theta \in G\) en el plano real\({\mathbb R}^2\) se dé girando el plano en sentido contrario a las agujas del reloj alrededor del origen a través de\(\theta\) radianes. Dejar\(P\) ser un punto en el plano distinto del origen.

1. Demostrar que\({\mathbb R}^2\) es un\(G\) -set.
2. Describir geométricamente la órbita que contiene\(P\text{.}\)
3. Encuentra el grupo\(G_P\text{.}\)

5

Supongamos que eso\(G\) actúa sobre sí mismo por conjugación; es decir,\(G = A_4\)\((g,h)~\mapsto~ghg^{-1}\text{.}\)

1. Determinar las clases de conjugación (órbitas) de cada elemento de\(G\text{.}\)
2. Determinar todos los subgrupos de isotropía para cada elemento de\(G\text{.}\)

6

Encuentra las clases de conjugación y la ecuación de clase para cada uno de los siguientes grupos.

1. \(\displaystyle S_4\)
2. \(\displaystyle D_5\)
3. \(\displaystyle {\mathbb Z}_9\)
4. \(\displaystyle Q_8\)

7

Escribe la ecuación de clase para\(S_5\) y para\(A_5\text{.}\)

8

Si un cuadrado permanece fijo en el plano, ¿de cuántas formas diferentes se pueden colorear las esquinas del cuadrado si se usan tres colores?

9

¿De cuántas formas se pueden colorear los vértices de un triángulo equilátero usando tres colores diferentes?

10

Encuentre el número de formas en que se puede construir un troquel de seis lados si cada lado está marcado de manera diferente con\(1, \ldots, 6\) puntos.

11

Hasta una rotación, ¿de cuántas formas se pueden colorear las caras de un cubo con tres colores diferentes?

12

Considera alambres\(12\) rectos de igual longitud con sus extremos soldados entre sí para formar los bordes de un cubo. Se puede usar alambre de plata o cobre para cada borde. ¿De cuántas formas diferentes se puede construir el cubo?

13

Supongamos que coloreamos cada una de las ocho esquinas de un cubo. Usando tres colores diferentes, ¿de cuántas formas se pueden colorear las esquinas hasta una rotación del cubo?

14

Cada una de las caras de un tetraedro regular se puede pintar ya sea de rojo o blanco. Hasta una rotación, ¿de cuántas formas diferentes se puede pintar el tetraedro?

15

Supongamos que los vértices de un hexágono regular deben ser coloreados ya sea de rojo o blanco. ¿De cuántas maneras se puede hacer esto hasta una simetría del hexágono?

16

Una molécula de benceno está compuesta por seis átomos de carbono y seis átomos de hidrógeno, unidos entre sí en forma hexagonal como en la Figura\(14.28\).

1. ¿Cuántos compuestos diferentes se pueden formar reemplazando uno o más de los átomos de hidrógeno por un átomo de cloro?
2. Encuentra el número de diferentes compuestos químicos que se pueden formar reemplazando tres de los seis átomos de hidrógeno en un anillo de benceno por un\(CH_3\) radical.

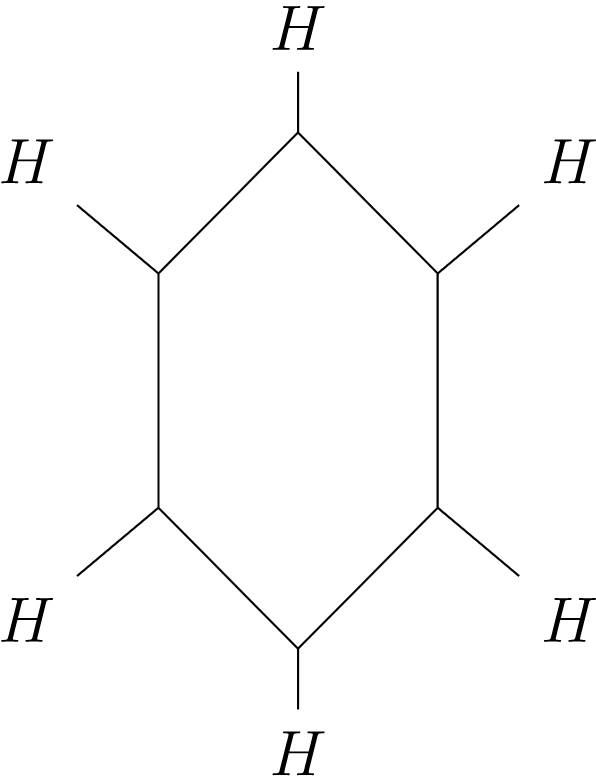
\(Figure \text { } 14.28.\)Un anillo de benceno

17

Cuántas clases de equivalencia de funciones de conmutación hay si las variables de entrada\(x_1\text{,}\)\(x_2\text{,}\) y\(x_3\) pueden permutarse por cualquier permutación en\(S_3\text{?}\) ¿Qué pasa si las variables de entrada\(x_1\text{,}\)\(x_2\text{,}\)\(x_3\text{,}\) y\(x_4\) pueden permutarse por cualquier permutación en\(S_4\text{?}\)

18

¿Cuántas clases de equivalencia de funciones de conmutación hay si las variables de entrada\(x_1\text{,}\)\(x_2\text{,}\)\(x_3\text{,}\) y\(x_4\) pueden permutarse por cualquier permutación en el subgrupo de\(S_4\) generados por la permutación\((x_1, x_2, x_3, x_4)\text{?}\)

19

Una corbata a rayas tiene\(12\) bandas de color. Cada banda puede ser coloreada por uno de los cuatro colores posibles. ¿Cuántas posibles corbatas de diferentes colores hay?

20

Un grupo actúa fielmente sobre un\(G\) -set\(X\) si la identidad es el único elemento de\(G\) que deja a cada elemento\(X\) fijo. Demostrar que\(G\) actúa fielmente sobre\(X\) si y solo si no hay dos elementos distintos de\(G\) tener la misma acción en cada elemento de\(X\text{.}\)

21

\(p\)Déjese ser prime. Demostrar que el número de diferentes grupos abelianos de orden\(p^n\) (hasta isomorfismo) es el mismo que el número de clases de conjugación en\(S_n\text{.}\)

22

Vamos a\(a \in G\text{.}\) mostrar eso para cualquier\(g \in G\text{,}\)\(gC(a) g^{-1} = C(gag^{-1})\text{.}\)

23

Seamos\(|G| = p^n\) un grupo no abeliano para\(p\) prime. Demostrar que\(|Z(G)| \lt p^{n - 1}\text{.}\)

24

Dejar\(G\) ser un grupo con orden\(p^n\) donde\(p\) es primo y\(X\) un finito\(G\) -set. Si el conjunto de elementos\(X_G = \{ x \in X : gx = x \text{ for all }g \in G \}\) está\(X\) fijado por la acción de grupo, entonces demuestre que\(|X| \equiv |X_G| \pmod{ p}\text{.}\)

25

Si\(G\) es un grupo de orden\(p^n\text{,}\) donde\(p\) es primo y\(n \geq 2\text{,}\) mostrar que\(G\) debe tener un subgrupo adecuado de orden\(p\text{.}\) Si\(n \geq 3\text{,}\) es cierto que\(G\) va a tener un subgrupo apropiado de orden\(p^2\text{?}\)