19.3: El álgebra de los circuitos eléctricos

Última actualización
Guardar como PDF

Page ID: 111267

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La utilidad de los álgebras booleanos se ha vuelto cada vez más evidente en las últimas décadas con el desarrollo de la computadora moderna. El diseño del circuito de los chips de computadora se puede expresar en términos de álgebras booleanas. En esta sección desarrollaremos el álgebra booleana de circuitos e interruptores eléctricos; sin embargo, estos resultados pueden generalizarse fácilmente al diseño de circuitos informáticos integrados.

Un interruptor es un dispositivo, ubicado en algún punto de un circuito eléctrico, que controla el flujo de corriente a través del circuito. Cada interruptor tiene dos estados posibles: puede estar abierto, y no permitir el paso de corriente a través del circuito, o un puede ser cerrado, y permitir el paso de corriente. Estos estados son mutuamente excluyentes. Requerimos que cada interruptor esté en un estado u otro, un interruptor no puede abrirse y cerrarse al mismo tiempo. Además, si un switch está siempre en el mismo estado que otro, denotaremos ambos por la misma letra; es decir, dos conmutadores que estén ambos etiquetados con la misma letra siempre$a$ estarán abiertos al mismo tiempo y cerrados al mismo tiempo.

Dados dos interruptores, podemos construir dos tipos fundamentales de circuitos. Dos interruptores$a$ y$b$ están en serie si conforman un circuito del tipo que se ilustra en la Figura$19.25$. La corriente puede pasar entre los terminales$A$ y$B$ en un circuito en serie solo si ambos interruptores$a$ y$b$ están cerrados. Denotaremos esta combinación de interruptores por$a \wedge b\text{.}$ Dos interruptores$a$ y$b$ están en paralelo si forman un circuito del tipo que aparece en la Figura$19.26$. En el caso de un circuito paralelo, la corriente puede pasar entre$A$ y$B$ si alguno de los interruptores está cerrado. Denotamos una combinación paralela de circuitos$a$ y$b$ por$a \vee b\text{.}$

$clipboard_ee55a276b702a98ed11ce74a6a9ec4214.png$

$Figure \text { } 19.25.$$a \wedge b$

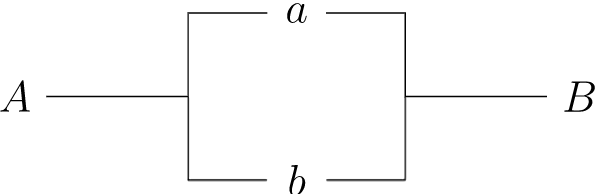
$clipboard_e14a7991a53145add6a510c6b72201807.png$

$Figure \text { } 19.26.$$a \vee b$

Podemos construir circuitos eléctricos más complicados a partir de circuitos en serie y paralelos reemplazando cualquier interruptor en el circuito por uno de estos dos tipos fundamentales de circuitos. Los circuitos construidos de esta manera se denominan circuitos serie-paralelo.

Consideraremos dos circuitos equivalentes si actúan igual. Es decir, si colocamos los conmutadores en circuitos equivalentes exactamente igual obtendremos el mismo resultado. Por ejemplo, en un circuito en serie$a \wedge b$ es exactamente lo mismo que$b \wedge a\text{.}$ Notar que esta es exactamente la ley conmutativa para álgebras booleanas. De hecho, el conjunto de todos los circuitos serie-paralelo forma un álgebra booleana bajo las operaciones de$\vee$ y$\wedge\text{.}$ Podemos usar diagramas para verificar los diferentes axiomas de un álgebra booleana. La ley distributiva,$a \wedge ( b \vee c ) = (a \wedge b ) \vee ( a \wedge c )\text{,}$ se ilustra en la Figura$19.27$. Si$a$ es un interruptor, entonces$a'$ es el interruptor que siempre está abierto cuando$a$ está cerrado y siempre cerrado cuando$a$ está abierto. Un circuito que siempre está cerrado está$I$ en nuestro álgebra; un circuito que siempre está abierto es$O\text{.}$ Las leyes para$a \wedge a' = O$ y se$a \vee a' = I$ muestran en$Figure 19.28$.

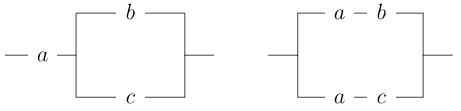
$clipboard_e6e2296c11fcd655712024cbcd49ffc0d.png$

$Figure \text { } 19.27.$$a \wedge ( b \vee c ) = (a \wedge b ) \vee ( a \wedge c )$

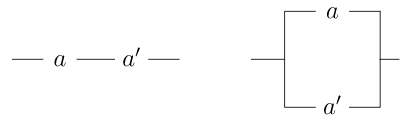
$clipboard_e4168dd26e32fbe6020dd1fb7ed27b4e9.png$

$Figure \text { } 19.28.$$a \wedge a' = O$y$a \vee a' = I$

Ejemplo$19.29$

Cada expresión booleana representa un circuito de conmutación. Por ejemplo, dada la expresión$(a \vee b) \wedge (a \vee b') \wedge (a \vee b)\text{,}$

Solución

podemos construir el circuito en la Figura$19.32$.

Teorema$19.30$

El conjunto de todos los circuitos es un álgebra booleana

Dejamos como ejercicio la prueba de este teorema para los axiomas de álgebra booleana aún no verificados. Ahora podemos aplicar las técnicas de álgebras booleanas a la teoría del cambio.

Ejemplo$19.31$

Dado un circuito complejo, ahora podemos aplicar las técnicas del álgebra booleana para reducirlo a uno más simple. Considera el circuito en la Figura$19.32$. Desde

\ begin {align*} (a\ vee b)\ wedge (a\ vee b')\ wedge (a\ vee b) & = (a\ vee b)\ wedge (a\ vee b)\ wedge (a\ vee b')\\ & = (a\ vee b)\ wedge (a\ vee b')\\ & = a\ vee (b\ wedge b')\ ')\\ & = a\ vee O\\ & = a\ text {,}\ end {alinear*}

Solución

podemos sustituir el circuito más complicado por un circuito que contenga el interruptor único$a$ y lograr la misma función.

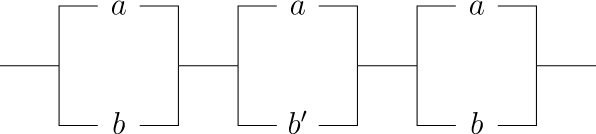
$clipboard_ebfde87e273368f1bbf2a962d8856b70e.png$

$Figure \text { } 19.32.$$(a \vee b) \wedge (a \vee b') \wedge (a \vee b)$

Nota Histórica

George Boole (1815—1864) fue la primera persona en estudiar celosías. En 1847, publicó La investigación de las leyes del pensamiento, libro en el que utilizó celosías para formalizar la lógica y el cálculo de las proposiciones. Boole creía que las matemáticas eran el estudio de la forma más que del contenido; es decir, no le preocupaba tanto lo que estaba calculando como por cómo lo estaba calculando. El trabajo de Boole fue llevado a cabo por su amigo Augustus De Morgan (1806—1871). De Morgan observó que el principio de dualidad a menudo se sostiene en la teoría de conjuntos, como lo ilustran las leyes de De Morgan para la teoría de conjuntos. Creía, al igual que Boole, que las matemáticas eran el estudio de los símbolos y las operaciones abstractas.

La teoría de conjuntos y la lógica fueron avanzadas aún más por matemáticos como Alfred North Whitehead (1861-1947), Bertrand Russell (1872—1970) y David Hilbert (1862-1943). En Principia Mathematica, Whitehead y Russell intentaron mostrar la conexión entre las matemáticas y la lógica mediante la deducción del sistema numérico natural de las reglas de la lógica formal. Si los números naturales pudieran determinarse a partir de la lógica misma, entonces también podría ser gran parte del resto de las matemáticas existentes. Hilbert intentó construir las matemáticas mediante el uso de la lógica simbólica de una manera que demostrara la consistencia de las matemáticas. Su planteamiento fue asestado un golpe mortal por Kurt Gödel (1906—1978), quien demostró que siempre habrá problemas “indecibles” en cualquier sistema axiomático suficientemente rico; es decir, que en cualquier sistema matemático de cualquier consecuencia, siempre habrá afirmaciones que nunca podrán probarse ni verdaderas ni falsas.

Como suele ocurrir, esta investigación básica en matemáticas puras posteriormente se volvió indispensable en una amplia variedad de aplicaciones. Los álgebras booleanos y la lógica se han vuelto esenciales en el diseño de los circuitos integrados a gran escala que se encuentran en los chips de computadora actuales. Los sociólogos han utilizado celosías y álgebras booleanas para modelar jerarquías sociales; los biólogos las han utilizado para describir biosistemas.