22.1: Estructura de un Campo Finito

Recordemos que un campo\(F\) tiene característica\(p\) si\(p\) es el entero positivo más pequeño tal que por cada elemento distinto de cero\(\alpha\) en\(F\text{,}\) tenemos\(p \alpha = 0\text{.}\) Si no existe tal entero, entonces\(F\) tiene característica\(0\text{.}\) Del Teorema \(16.19\)sabemos que\(p\) debe ser prime. Supongamos que\(F\) es un campo finito con\(n\) elementos. Entonces\(n \alpha = 0\) para todos\(\alpha\) en\(F\text{.}\) Consecuentemente, la característica de\(F\) debe ser\(p\text{,}\) donde\(p\) es un primo dividiendo\(n\text{.}\) Esta discusión se resume en la siguiente proposición.

Proposición\(22.1\).

Si\(F\) es un campo finito, entonces la característica de\(F\) es\(p\text{,}\) donde\(p\) es primo.

 

A lo largo de este capítulo asumiremos que\(p\) es un número primo a menos que se indique lo contrario.

Proposición\(22.2\).

Si\(F\) es un campo finito de característica\(p\text{,}\) entonces el orden de\(F\) es\(p^n\) para algunos\(n \in {\mathbb N}\text{.}\)

Prueba

Dejar\(\phi : {\mathbb Z} \rightarrow F\) ser el homomorfismo anular definido por\(\phi(n) = n \cdot 1\text{.}\) Dado que la característica de\(F\) es\(p\text{,}\) el núcleo de\(\phi\) debe ser\(p {\mathbb Z}\) y la imagen de\(\phi\) debe ser un subcampo de\(F\) isomórfico a\({\mathbb Z}_p\text{.}\) Denotaremos este subcampo por\(K\text{.}\) Desde \(F\)es un campo finito, debe ser una extensión finita de\(K\) y, por lo tanto, una extensión algebraica de\(K\text{.}\) Supongamos que\([F : K] = n\) es la dimensión de\(F\text{,}\) donde\(F\) es un espacio\(K\) vectorial. Deben existir elementos\(\alpha_1, \ldots, \alpha_n \in F\) tales que cualquier elemento\(\alpha\) en\(F\) pueda escribirse de manera única en la forma

\[ \alpha = a_1 \alpha_1 + \cdots + a_n \alpha_n\text{,} \nonumber \]

donde están los\(a_i\)'s en\(K\text{.}\) Dado que hay\(p\) elementos en\(K\text{,}\) hay\(p^n\) posibles combinaciones lineales de los s.\(\alpha_i\) por lo tanto, el orden de\(F\) debe ser\(p^n\text{.}\)

Lema\(22.3\). Freshman's Dream

\(p\)Sea primo y\(D\) sea un dominio integral de característica\(p\text{.}\) Entonces

\[ a^{p^n} + b^{p^n} = (a + b)^{p^n} \nonumber \]

para todos los enteros positivos\(n\text{.}\)

Prueba

Vamos a probar este lema usando inducción matemática en\(n\text{.}\) Podemos usar la fórmula binomial (ver Capítulo 2, Ejemplo\(2.4\)) para verificar el caso para\(n = 1\text{;}\) eso es,

\[ (a + b)^p = \sum_{k = 0}^{p} \binom{p}{k} a^k b^{p - k}\text{.} \nonumber \]

Si\(0 \lt k \lt p\text{,}\) entonces

\[ \binom{p}{k} = \frac{p!}{k!(p - k)!} \nonumber \]

debe ser divisible por\(p\text{,}\) ya que\(p\) no se puede dividir\(k!(p - k)!\text{.}\) Tenga en cuenta que\(D\) es un dominio integral de característica\(p\text{,}\) por lo que todos menos el primer y último términos en la suma deben ser cero. Por lo tanto,\((a + b)^p = a^p + b^p\text{.}\)

Ahora supongamos que el resultado se mantiene para todos\(k\text{,}\) donde\(1 \leq k \leq n\text{.}\) Por la hipótesis de inducción,

\[ (a + b)^{p^{n + 1}} = ((a + b)^p)^{p^{n}} = (a^p + b^p)^{p^{n}} = (a^p)^{p^{n}} + (b^p)^{p^{n}} = a^{p^{n + 1}} + b^{p^{n + 1}}\text{.} \nonumber \]

Por lo tanto, el lema es cierto\(n + 1\) y la prueba está completa.

Que\(F\) sea un campo. Un polinomio\(f(x) \in F[x]\) de grado\(n\) es separable si tiene raíces\(n\) distintas en el campo de división de es\(f(x)\text{;}\) decir,\(f(x)\) es separable cuando se facciona en distintos factores lineales sobre el campo de división de\(f\text{.}\) Una extensión\(E\) de \(F\)es una extensión separable de\(F\) si cada elemento en\(E\) es la raíz de un polinomio separable en\(F[x]\text{.}\)

Ejemplo\(22.4\).

El polinomio\(x^2 - 2\) es separable\({\mathbb Q}\) ya que tiene\((x - \sqrt{2}\, )(x + \sqrt{2}\, )\text{.}\) en cuenta como De hecho,\({\mathbb Q}(\sqrt{2}\, )\) es una extensión separable de\({\mathbb Q}\text{.}\) Let\(\alpha = a + b \sqrt{2}\) be any element in\({\mathbb Q}(\sqrt{2}\, )\text{.}\) If\(b = 0\text{,}\) then

Solución

\(\alpha\)es una raíz de\(x - a\text{.}\) Si\(b \neq 0\text{,}\) entonces\(\alpha\) es la raíz del polinomio separable

\[ x^2 - 2 a x + a^2 - 2 b^2 = (x - (a + b \sqrt{2}\, ))(x - (a - b \sqrt{2}\, ))\text{.} \nonumber \]

Afortunadamente, tenemos una prueba fácil para determinar la separabilidad de cualquier polinomio. Vamos

\[ f(x) = a_0 + a_1 x + \cdots + a_n x^n \nonumber \]

ser cualquier polinomio en\(F[x]\text{.}\) Definir la derivada\(f(x)\) de ser

\[ f'(x) = a_1 + 2 a_2 x + \cdots + n a_n x^{n - 1}\text{.} \nonumber \]

Lema\(22.5\).

Dejar\(F\) ser un campo y\(f(x) \in F[x]\text{.}\) Entonces\(f(x)\) es separable si y solo si\(f(x)\) y\(f'(x)\) son relativamente primos.

Prueba

Que\(f(x)\) sean separables. Luego\(f(x)\) factores sobre algún campo de extensión de\(F\) como\(f(x) = (x - \alpha_1) (x - \alpha_2) \cdots (x - \alpha_n)\text{,}\) dónde\(\alpha_i \neq \alpha_j\) para\(i \neq j\text{.}\) Tomando la derivada de\(f(x)\text{,}\) vemos que

\ begin {align*} f' (x) & = (x -\ alpha_2)\ cdots (x -\ alpha_n)\\ & + (x -\ alpha_1) (x -\ alpha_3)\ cdots (x -\ alpha_n)\\ & +\ cdots + (x -\ alpha_1)\ cdots (x -\ alpha_ {n - 1})\ texto {.} \ end {align*}

De ahí,\(f(x)\) y no\(f'(x)\) pueden tener factores comunes.

Para probar lo contrario, demostraremos que lo contrapositivo de la afirmación es cierto. Supongamos que\(f(x) = (x - \alpha)^k g(x)\text{,}\) donde\(k \gt 1\text{.}\) Diferenciar, tenemos

\[ f'(x) = k ( x - \alpha)^{k-1} g(x) + (x- \alpha)^k g'(x)\text{.} \nonumber \]

Por lo tanto,\(f(x)\) y\(f'(x)\) tienen un factor común.

Teorema\(22.6\).

Por cada primo\(p\) y cada entero positivo\(n\text{,}\) existe un campo finito\(F\) con\(p^n\) elementos. Además, cualquier campo de orden\(p^n\) es isomórfico al campo de división de\(x^{p^n} -x\) más de\({\mathbb Z}_p\text{.}\)

Prueba

Dejar\(f(x) = x^{p^n} - x\) y dejar\(F\) ser el campo de división de\(f(x)\text{.}\) Entonces por Lema 22.5,\(f(x)\) tiene ceros\(p^n\) distintos en\(F\text{,}\) ya que\(f'(x) = p^n x^{p^n - 1} - 1 = -1\) es relativamente primo a\(f(x)\text{.}\) Afirmamos que las raíces de\(f(x)\) forman un subcampo de\(F\text{.}\) Ciertamente 0 y 1 son ceros de \(f(x)\text{.}\)Si\(\alpha\) y\(\beta\) son ceros de\(f(x)\text{,}\) entonces\(\alpha + \beta\) y también\(\alpha \beta\) son ceros de\(f(x)\text{,}\) desde\(\alpha^{p^n} + \beta^{p^n} = (\alpha + \beta)^{p^n}\) y También\(\alpha^{p^n} \beta^{p^n} = (\alpha \beta)^{p^n}\text{.}\) necesitamos demostrar que la inversa aditiva y la inversa multiplicativa de cada raíz de\(f(x)\) son raíces de\(f(x)\text{.}\) Para cualquier cero\(\alpha\) de\(f(x)\text{,}\) sabemos que también\(-\alpha\) es un cero de\(f(x)\text{,}\) desde

\[ f(-\alpha) = (-\alpha)^{p^n} - (-\alpha) = -\alpha^{p^n} + \alpha = -(\alpha^{p^n} - \alpha) = 0\text{,} \nonumber \]

siempre que\(p\) sea impar. Si\(p = 2\text{,}\) entonces

\[ f(-\alpha) = (-\alpha)^{2^n} - (-\alpha) = \alpha + \alpha = 0\text{.} \nonumber \]

Si\(\alpha \neq 0\text{,}\) entonces\((\alpha^{-1})^{p^n} = (\alpha^{p^n})^{-1} = \alpha^{-1}\text{.}\) Dado que los ceros\(f(x)\) forman un subcampo de\(F\) y\(f(x)\) se divide en este subcampo, el subcampo debe ser todo de\(F\text{.}\)

Dejar\(E\) ser cualquier otro campo de orden\(p^n\text{.}\) Para mostrar que\(E\) es isomórfico a\(F\text{,}\) debemos demostrar que cada elemento en\(E\) es una raíz de\(f(x)\text{.}\) Ciertamente 0 es una raíz de\(f(x)\text{.}\) Let\(\alpha\) be un elemento distinto de cero de\(E\text{.}\) El orden del grupo multiplicativo de elementos distintos de cero de\(E\) es\(p^n-1\text{;}\) por lo tanto,\(\alpha^{p^n-1} =1\) o\(\alpha^{p^n} -\alpha = 0\text{.}\) Dado que\(E\) contiene\(p^n\) elementos,\(E\) debe ser un campo de división de\(f(x)\text{;}\) sin embargo, por Corolario 21.36, el campo de división de cualquier polinomio es único hasta el isomorfismo.

El campo finito único con\(p^n\) elementos se llama el campo de orden Galois\(p^n\text{.}\) Denotaremos este campo por\(\gf(p^n)\text{.}\)

Teorema\(22.7\).

Cada subcampo del campo Galois\(\gf(p^n)\) tiene\(p^m\) elementos, donde\(m\) divide\(n\text{.}\) Por el contrario, si\(m \mid n\) para\(m \gt 0\text{,}\) entonces existe un subcampo único de\(\gf(p^n)\) isomórfico a\(\gf(p^m)\text{.}\)

Prueba

Dejar\(F\) ser un subcampo de\(E = \gf(p^n)\text{.}\) Entonces\(F\) debe ser una extensión de campo de\(K\) que contenga\(p^m\) elementos, donde\(K\) es isomórfico a\({\mathbb Z}_p\text{.}\) Entonces\(m \mid n\text{,}\) desde\([E:K] = [E:F][F:K]\text{.}\)

Para probar lo contrario, supongamos que\(m \mid n\) para algunos\(m \gt 0\text{.}\) Entonces\(p^m -1\) divide\(p^n -1\text{.}\) Consecuentemente,\(x^{p^m -1} - 1\) divide\(x^{p^n -1} -1\text{.}\) Por lo tanto,\(x^{p^m} - x\) debe dividir\(x^{p^n} - x\text{,}\) y cada cero de\(x^{p^m} - x\) es también un cero de\(x^{p^n} - x\text{.}\) Así,\(\gf(p^n)\) contiene, como subcampo, un campo de división de\(x^{p^m} - x\text{,}\) los cuales debe ser isomórfico a\(\gf(p^m)\text{.}\)

Ejemplo\(22.8\).

La celosía de los subcampos de\(\gf(p^{24})\) se da en la Figura\(22.9\).

Solución

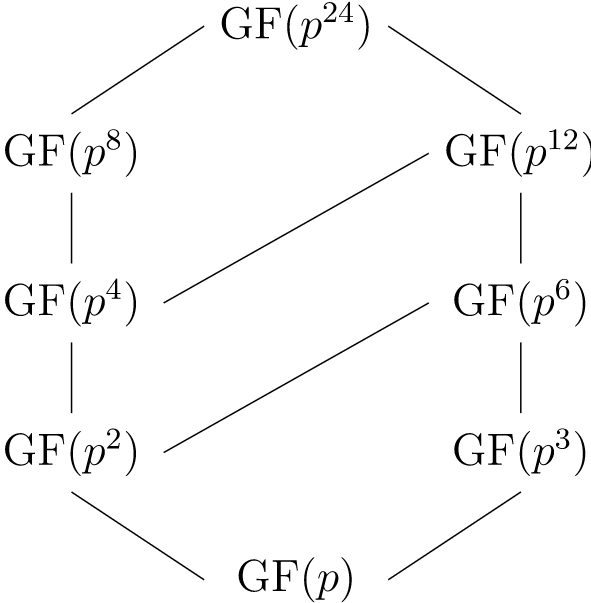
\(Figure \text { } 22.9.\)Subcampos de\(\gf(p^{24})\)

Con cada campo\(F\) tenemos un grupo multiplicativo de elementos distintos de cero de los\(F\) cuales denotaremos por\(F^*\text{.}\) El grupo multiplicativo de cualquier campo finito es cíclico. Este resultado se desprende del resultado más general que probaremos en el próximo teorema.

Teorema\(22.10\).

Si\(G\) es un subgrupo finito\(F^\ast\text{,}\) del grupo multiplicativo de elementos distintos de cero de un campo\(F\text{,}\) entonces\(G\) es cíclico.

Prueba

\(G\)Sea un subgrupo finito\(F^\ast\) de orden\(n\text{.}\) Por el Teorema Fundamental de Grupos Abelianos Finitos (Teorema\(13.4\)),

\[ G \cong {\mathbb Z}_{p_1^{e_1}} \times \cdots \times {\mathbb Z}_{p_k^{e_k}}\text{,} \nonumber \]

donde\(n = p_1^{e_1} \cdots p_k^{e_k}\) y los\(p_1, \ldots, p_k\) son (no necesariamente distintos) primos. Dejar\(m\) ser el mínimo común múltiplo de\(p_1^{e_1}, \ldots, p_k^{e_k}\text{.}\) Entonces\(G\) contiene un elemento de orden\(m\text{.}\) Ya que cada\(\alpha\) en\(G\) satisface\(x^r - 1\) para alguna\(r\) división también\(m\text{,}\)\(\alpha\) debe ser una raíz de\(x^m - 1\text{.}\) Desde\(x^m -1\) tiene a lo sumo \(m\)raíces\(F\text{,}\)\(n \leq m\text{.}\) en Por otro lado, sabemos que\(m \leq |G|\text{;}\) por lo tanto,\(m = n\text{.}\) Así,\(G\) contiene un elemento de orden\(n\) y debe ser cíclico.

Corolario\(22.11\).

El grupo multiplicativo de todos los elementos distintos de cero de un campo finito es cíclico.

Corolario\(22.12\).

Cada extensión finita\(E\) de un campo finito\(F\) es una extensión simple de\(F\text{.}\)

Prueba

Dejar\(\alpha\) ser un generador para el grupo cíclico\(E^{\ast}\) de elementos distintos de cero de\(E\text{.}\) Entonces\(E = F( \alpha )\text{.}\)

Ejemplo\(22.13\).

El campo finito\(\gf(2^4)\) es isomórfico al campo\({\mathbb Z}_2/ \langle 1 + x + x^4 \rangle\text{.}\) Por lo tanto, los elementos de\(\gf(2^4)\) pueden tomarse para ser

\[ \{ a_0 + a_1 \alpha + a_2 \alpha^2 + a_3 \alpha^3 : a_i \in {\mathbb Z}_2 \text{ and } 1 + \alpha + \alpha^4 = 0 \}\text{.} \nonumber \]

Solución

Recordando que\(1 + \alpha +\alpha^4 = 0\text{,}\) sumamos y multiplicamos elementos de\(\gf(2^4)\) exactamente como sumamos y multiplicamos polinomios. El grupo multiplicativo de\(\gf(2^4)\) es isomórfico a\({\mathbb Z}_{15}\) con generador\(\alpha\text{:}\)

\ begin {alinear*} &\ alfa^1 =\ alfa y &\ alfa^6 =\ alfa^2 +\ alfa^3 & &\ alfa^ {11} =\ alfa +\ alfa^2 +\ alfa^3 &\\ &\ alfa^2 =\ alfa^2 & &\ alfa^7 = 1 +\ alfa +\ alfa^3 &\ alfa^ {12} = 1 + alfa\ +\ alfa^2 +\ alfa^3 &\\ &\ alfa^3 =\ alfa^3 & &\ alfa^8 = 1 +\ alfa^2 & &\ alfa^ {13} = 1 +\ alfa^2 +\ alfa^3 &\\ &\ alfa^4 = 1 +\ alfa & &\ alfa^9 =\ alfa +\ alfa^3 &\ alfa^4 = 1 +\ alfa^3 &\\ alfa^5 = alfa +\ alfa^2 & alfa^2 & alfa^^ {10} = 1 +\ alfa +\ alfa^2 & &\ alfa^ {15} = 1. &\ end {alinear*}