1.1: Números Complejos

Los números complejos fueron originalmente inventados para resolver problemas en álgebra. Posteriormente se reconoció que el álgebra de números complejos proporciona un elegante conjunto de herramientas para la geometría en el plano. En esta sección se presentan los fundamentos del álgebra y geometría de los números complejos.

Los elementos en el conjunto de números complejos\(\mathbb{C}\) están en correspondencia uno a uno con puntos en el plano real bidimensional\(\mathbb{R}^{2}\) (donde\(\mathbb{R}\) denota el conjunto de números reales). Escribiremos\(z\leftrightarrow (x,y)\) para denotar que el número complejo\(z\) corresponde al par ordenado\((x,y)\) de números reales.

Partes reales e imaginarias

Dado un número complejo\(z\) correspondiente al punto\((x,y)\) en\(\mathbb{R}^{2}\), decimos que\(x\) es la parte real de\(z\) y esa\(y\) es la parte imaginaria de\(z\), denotado\(Re\left ( z \right )=x\) y\(Im⁡(z)=y\). El conjunto\(\mathbb{C}\) contiene el conjunto\(\mathbb{R}\) como un subconjunto. El número real\(x\), que también es el número complejo\(x\), corresponde al par ordenado\((x,0)\). Un número complejo que corresponde a un par ordenado\((0,y)\) se llama imaginario (puro). El número complejo i corresponde al par ordenado\((0,1)\). Aquí hay un resumen hasta el momento.

\ begin {align*}
z &\ leftrightarrow (Re\ left (z\ right), Im\ left (z\ right))\\
x\ in\ mathbb {R} &\ leftrightarrow (x,0)\\
i &\ left trightarrow (0.1)
\ end {align*}

Módulo y argumento

Figura 1.1.1. La norma y el argumento de un número complejo son coordenadas polares.

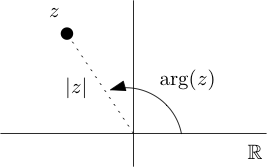
Dado un número complejo\(z\leftrightarrow (x,y)\text{,}\) dejan\((r,\theta)\) ser coordenadas polares para el punto\((x,y)\) tal que\(r≥0\) y\(θ\) se mide en radianes. El módulo o norma de\(z\text{,}\) denotado\(|z|\), se define como la coordenada polar\(r=\sqrt{x^2+y^2}\) y el argumento de\(z\text{,}\) denotado\(\arg(z)\), es el polar coordenada\(θ\), es decir, el ángulo orientado hecho por el vector real\((x,y)\) con el eje real positivo. Es decir,\((|z|,\arg{z})\) son coordenadas polares para el punto\((x,y)\text{.}\) Ver Figura 1.1.1. Aquí hay un resumen.

Norma y argumento.

\ [
z\ leftrightarrow (x, y) =\ izquierda (|z|\ cos (\ arg {z}), |z|\ sin (\ arg {z})\ derecha)\ label {normargdef}\ tag {1.1.1}
\]

Suma y multiplicación de números complejos

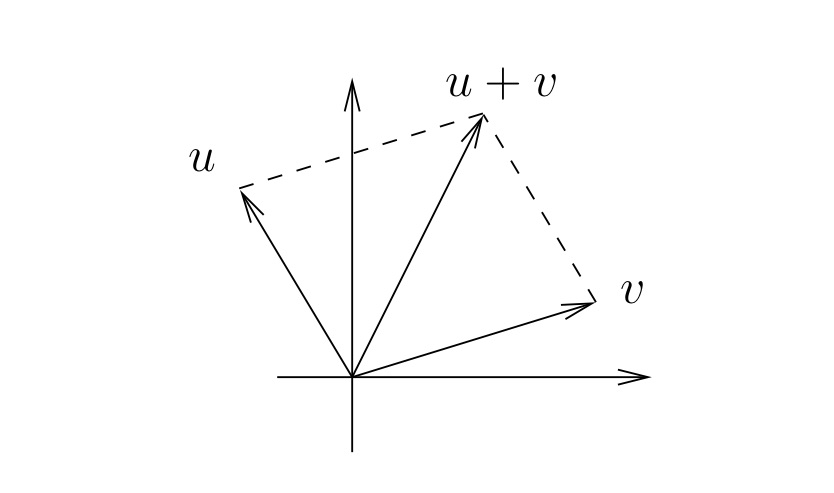
Dados los números complejos\(z\leftrightarrow (x,y)\) y\(z'\leftrightarrow(x',y')\text{,}\) la suma\(z+z'\) se define por lo siguiente.

Adición compleja.

\ [
z+z'\ leftrightarrow (x+x', y+y')\ label {complexadddef}\ tag {1.1.2}
\]

En otras palabras, la adición compleja corresponde a la adición de vector real. Ver Figura 1.1.2.

Figura 1.1.2. La adición del complejo es la adición del vector

El producto\(zz'\) se define de la siguiente manera.

Multiplicación compleja.

\ begin {align}
|zz'| & = |z||z'|\ label {complexmultdefnorm}\ tag {1.1.3}\\
\ arg (zz') & =\ arg {z} +\ arg {z'}\ label {complexmultdefarg}\ tag {1.1.4}
\ end {align}

La interacción entre la adición compleja y la multiplicación se expresa por la siguiente relación, la cual se mantiene para cualquier complejo\(z,u,v\text{.}\) Ver Figura 1.1.3.

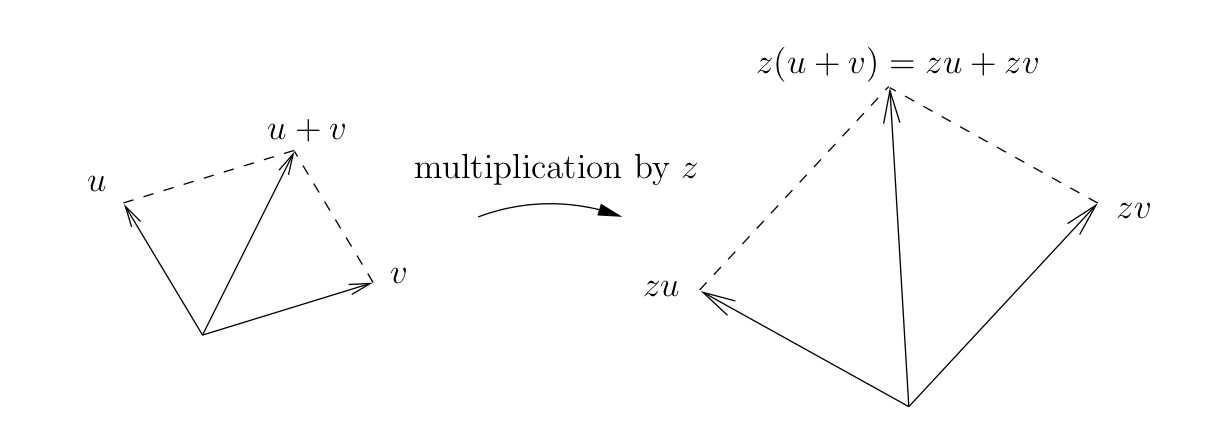
Derecho distributivo.

\ [
z (u+v) = zu+zv\ label {distributivelaw}\ tag {1.1.5}
\]

Figura 1.1.3. La ley distributiva: la multiplicación por\(z\) gira los vectores\(u\text{,}v\text{,}\) y\(u+v\) por ángulo\(\arg z\) y escalas por el factor\(|z|\text{.}\)

A continuación se presentan una serie de relaciones que surgen de las definiciones de suma y multiplicación complejas. \(a,b,c,d\)Dejen ser números reales y dejar que\(z,u,v\) sean números complejos. Se mantienen las siguientes relaciones. ¹

\ begin {align}
a+ib &\ leftrightarrow (a, b)\ tag {1.1.6}\\
a+b\;\;\ text {(suma compleja)} &= a+b\;\;\ text {(suma real)}\ label {addextiende}\ tag {1.1.7}\
ab\;\;\ text {(producto complejo)} & = ab\;\ texto {(producto real)}\ label {multextends}\ tag {1.1.8}\\
|a|\;\;\ text {(norma compleja)} & = |a|\;\;\ text {(valor absoluto real)}\ label {normextends}\ tag {1.1.9}\\
1z & = z1 = z\ label {multidentidad}\ tag {1.1.10}\
i^2 & = -1\ etiqueta {i2isminus1}\ tag {1.1.11}\\
(a+ib) + (c+id) & = (a+c) + i (b+d)\ tag {1.1.12}\\
(a+ib) (c+id) & = (ac-bd) + i (ad+bc)\ label {complexmultrectangular}\ tag {1.1.13}
\ end {align}

La función exponencial compleja

La serie Taylor para la función real\(y=e^x\) es

\ [
e^x = 1 +x +\ frac {x^2} {2} +\ frac {x^3} {3!} +\ cdots.
\ nonumber\]

La convergencia para secuencias y series de números complejos se puede definir de manera que extienda naturalmente las definiciones para números reales. Resulta que la serie de potencia compleja

\ [
1 +z +\ frac {z^2} {2} +\ frac {z^3} {3!} +\ cdots
\ nonumber\]

converge para cada número complejo\(z\text{,}\) por lo que definimos la función exponencial compleja por

\ [
e^z= 1 +z +\ frac {z^2} {2} +\ frac {z^3} {3!} +\ cdots.
\ nonumber\]

El exponencial complejo obedece las leyes familiares de lo exponencial real. Para\(z,w\) en\(\mathbb{C}\), tenemos

\ begin {alinear*}
e^ze^w & = e^ {z+w}\\
e^0 & =1
\ end {alinear*}

Una propiedad clave del complejo exponencial es la siguiente, llamada fórmula de Euler.

La fórmula de Euler.

\ [
e^ {it} =\ cos t + i\ sin t\;\;\ text {(por $t$ reales)}\ label {eulersformula}\ tag {1.1.14}
\]

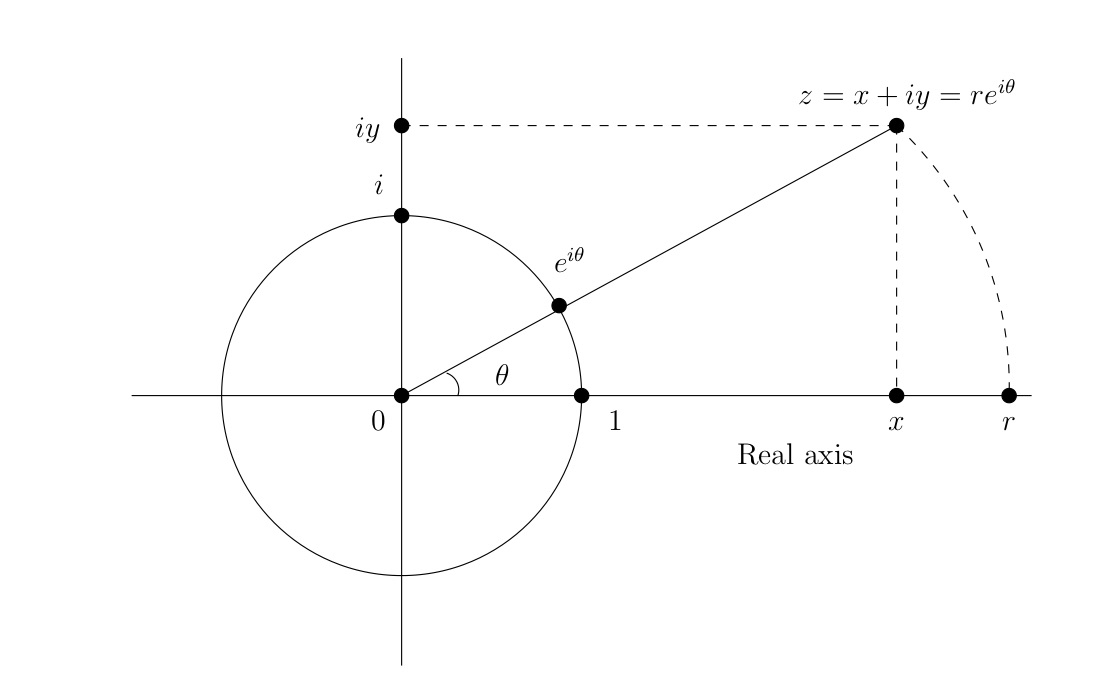
Para\(z\) con\(r=|z|\) y\(t=\arg(z)\text{,}\) la expresión\(z=re^{it}\) se llama la forma polar para\(z\text{.}\) Por el contrario, llamamos a\(z=x+iy\) la forma rectangular (o la forma cartesiana ) para\(z\text{.}\) la Figura 1.1.4 muestra un resumen del contenido geométrico de las formas rectangulares y polares para un número complejo\(z\text{.}\)

Así es como se ve la multiplicación compleja en forma polar. Para\(z=re^{i\theta}, w=se^{i\phi}\text{,}\) nosotros tenemos

\ [
zw = (re^ {i\ theta}) (se^ {i\ phi}) = rse^ {i (\ theta +\ phi)}. \ label {complexmultpolar}\ tag {1.1.15}
\]

A partir de esto es fácil ver que para\(r\neq 0\text{,}\) nosotros tenemos

\ [
\ izquierda (re^ {i\ theta}\ derecha)\;\ izquierda (\ frac {1} {r} e^ {-i\ theta}\ derecha) = 1.
\ nonumber\]

Porque\(z=re^{i\theta}\) con\(r\neq 0\text{,}\) llamamos\(\frac{1}{r}e^{-i\theta}\) al inverso multiplicativo de\(z\text{,}\) denotado\({1}/{z}\) o\(z^{-1}\text{.}\)

Figura 1.1.4. Formas rectangulares y polares para un número complejo\(z\)

Conjugación

El conjugado del número complejo\(z=x+iy=re^{i\theta}\text{,}\) denotado\(\overline{z}\) o\(z^\ast\), se define como\(z^\ast = x-iy = re^{-i\theta}\text{.}\) Geométricamente,\(z^\ast\) es la reflexión de\(z\) a través del eje real (el\(x\) -eje) en\(\mathbb{R}^{2}\). Aquí hay algunas relaciones que involucran conjugados.

\ begin {align}
Re (z) & =\ frac {z + z^\ ast} {2}\ label {realpartformula}\ tag {1.1.16}\
Im (z) & =\ frac {z - z^\ ast} {2i}\ label {imagpartformula}\ tag {1.1.17}\\
|z|^2 & = zz^\ ast\ label {zzbarie {zzbarie snormsq}\ tag {1.1.18}\\
2\ arg z & =\ frac {z} {z^\ ast}\;\;\ text {(for $z\ neq 0$)}\ tag {1.1.19}\\
\ frac {1} {z}
& =\ frac {z^\ ast} {zz^\ ast} =\ frac {z^\ ast} {|z|^2}\;\;\ text {(para $z\ neq 0$)}\ tag {1.1.20}\\
(w) ^\ ast & = z^\ ast w^\ ast\ tag {1.1.21}
\ end {align}

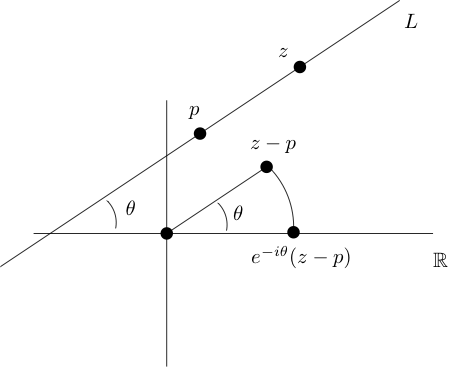
Círculos y líneas

Dejar\(C\) ser el círculo de radio\(r\gt 0\) y con centro\(a\in \mathbb{C}\text{.}\) Un punto\(z\) se encuentra sobre\(C\) si y sólo si la distancia desde\(z\) a a es igual\(r\text{.}\) En símbolos matemáticos,\(C\) es el conjunto de soluciones\(z\) para la siguiente ecuación.

\ [
|z-a|=r\ etiqueta {circleeqn}\ tag {1.1.22}
\]

La línea real\(\mathbb{R}\) es el conjunto de soluciones\(z\) de la ecuación\(Im⁡(z)=0\). De manera más general, deja\(L\) ser una línea que contiene el punto\(p\in \mathbb{C}\) y hace un ángulo\(\theta\) con el eje real (establecer\(\theta=0\) si\(L\) es paralela al eje real). Si\(z\in L\text{,}\) entonces\(e^{-i\theta}(z-p)\) es real, entonces\(Im(e^{-i\theta}(z-p))=0\text{.}\) Ver Figura 1.1.5. Por el contrario, si\(e^{-i\theta}(z-p)\) es real, entonces\(z\) se encuentra en\(L\text{.}\) Multiplicar por una constante positiva\(k\text{,}\)\(a=ke^{-i\theta}\) y establecer y,\(b=-ke^{-i\theta}p\text{,}\) concluimos que la línea\(L\) es el conjunto de soluciones a la siguiente ecuación.

\ [
Im (az+b) =0\ etiqueta {lineeqn}\ etiqueta {1.1.23}
\]

Figura 1.1.5. Una línea en el plano complejo.

Ejercicios

Ejercicio 1

¿Cuál es la diferencia entre las coordenadas polares y la forma polar? ¿Cuál es la diferencia entre las coordenadas rectangulares y la forma rectangular? Escribe fórmulas para convertir de coordenadas polares a rectangulares y viceversa.

Solución

Let\(z\) be a complex number, let\(x=Re(z)\text{,}\)\(y=Im(z)\text{,}\)\(r=|z|\) and\(\theta = \arg(z)\text{.}\) The pair\((r,θ)\) is called the polar coordinates for\(z\text{,}\) while the expression\(re^{i\theta}\) is called the polar form for\(z\text{.}\) The pair\((x,y)\) is called the rectangular coordinates for\(z\text{,}\) mientras que la expresión\(x+iy\) se llama la forma rectangular para\(z\text{.}\)

Para convertir de polar a rectangular, utilice las ecuaciones\(x=r\cos \theta, y=r\sin \theta\) (mostrar bocetos para explicar estas fórmulas). Para convertir de rectangular a polar, use\(r=\sqrt{x^2+y^2}\) y\(\tan \theta = y/x\text{.}\) Para la última ecuación, debe usar juicio cuándo\(x=0\) decidir si\(θ\) debe ser\(\pi/2\) o También\(-\pi/2\text{.}\) debe usar juicio al calcular\(\theta = \arctan (y/x)\text{.}\) El codominio estándar para arctan es el intervalo \((\pi/2,\pi/2)\text{,}\)por lo que necesita usar\(\theta = \arctan (y/x) + \pi\) para\(x\lt 0\text{.}\)

Ejercicio 2

Exprese cada uno de los siguientes en forma rectangular y polar.

a.\(\displaystyle 3(2-i) + 6(1+i)\)

b.\(\displaystyle \left(2e^{i\pi/6}\right)\left(3e^{-i\pi/3}\right)\)

c.\(\displaystyle (2+3i)(4-i)\)

d.\(\displaystyle (1+i)^3\)

Responder

a.\(\displaystyle 12+3i=\sqrt{153}\;e^{i\arctan(1/4)}\)

b.\(\displaystyle 6e^{-i\pi/6}=3\sqrt{3}-3i\)

c.\(\displaystyle 11+10i=\sqrt{221}\;e^{i\arctan(10/11)}\)

d.\(\displaystyle -2+2i=2\sqrt{2}\;e^{i3\pi/4}\)

Ejercicio 3

Demostrar la siguiente propiedad de norma.

La desigualdad triangular.

Para dos números complejos\(z,w\text{,}\) tenemos

\ (\ [
|z+w|\ leq |z|+|w|.
\ nonumber\]\)

Solución

El enfoque más simple es geométrico: Esboza el paralelogramo para la adición de vectores y usa el hecho de que la longitud de cualquier lado de un triángulo es menor que la suma de las longitudes de los otros dos lados.

Aquí hay una ruta a una prueba algebraica: Dejar\(z=a+bi\text{,}\)\(w=c+di\text{.}\) Manipular la desigualdad del triángulo (comience por cuadrar ambos lados) para obtener

\ (\ [
2abcd\ leq b^2c^2 + a^2d^2.
\ nonumber\]\)

Esto es lo mismo que la afirmación claramente verdadera

\ [
0\ leq b^2c^2 + a^2d^2 - 2abcd = (bc-ad) ^2.
\ nonumber\]

Concluya observando que todos los pasos de la derivación son reversibles.

Ejercicio 4

Demostrar (1.1.18).

Solución

Vamos\(z=re^{i\theta}\text{.}\) Entonces\(\overline{z}=re^{-i\theta}\text{,}\) y tenemos

\ begin {align*}
z\ overline {z} & = re^ {i\ theta} re^ {-i\ theta}\\
& = r^2 e^0\\
& = r^2 = |z|^2.
\ end {align*}

Ejercicio 5

Dejar\(p\) y\(q\) ser números complejos. Demostrar que la distancia (distancia ordinaria entre puntos en el plano) entre\(p\) y\(q\) es\(|p-q|\text{.}\)

Pista

Use forma rectangular.

Solución

Vamos\(p=a+ib\) y\(q=c+id\text{.}\) tenemos

\ begin {align*}
|p-q| & = | (a+ib) - (c+id) |\\
& = | (a-c) +i (b-d) |\\
& =\ sqrt {(a-c) ^2 + (b-d) ^2}.
\ end {align*}

Esta última expresión es la distancia de\(p\) a\(q\text{,}\) así que terminamos.

Ejercicio 6

Exprese cada uno de los siguientes en forma rectangular y polar.

a.\(\displaystyle \displaystyle \frac{2+i}{3-i}\)

b.\(\displaystyle \displaystyle \frac{1+2i}{1-2i}\)

c.\(\displaystyle \displaystyle \frac{2e^{i\pi/4}}{3e^{-i\pi/2}}\)

Responder

a.\(\displaystyle \displaystyle \frac{1}{2} + \frac{1}{2}i=\frac{\sqrt{2}}{2}e^{i\pi/4}\)

b.\(\displaystyle \displaystyle -\frac{3}{5} +\frac{4}{5}i=e^{i(\arctan(-4/3)+\pi)}\)

c.\(\displaystyle \displaystyle \frac{2}{3}e^{i3\pi/4}=-\frac{\sqrt{2}}{3} + \frac{\sqrt{2}}{3}i\)

Ejercicio 7

Verificar las fórmulas (1.1.16) y (1.1.17).

Solución

Vamos\(z=x+iy\text{.}\) Entonces tenemos

• \(\displaystyle \frac{z+\overline{z}}{2}= \frac{2x}{2}=x=Re(z)\text{,}\)y
• \(\displaystyle \frac{z-\overline{z}}{2i}=\frac{2iy}{2i}=y=Im(z)\text{.}\)

Ejercicio 8

Dado un número complejo distinto de cero\(z\text{,}\) explicar por qué\(z\) tiene exactamente dos raíces cuadradas, y explicar cómo encontrarlas.

Solución

Ya que al cuadrar un número cuadra la norma y duplica el argumento, se puede encontrar una raíz cuadrada tomando la raíz cuadrada de la norma y dividiendo el argumento por dos. Es decir, para\(z=re^{i\theta}\text{,}\) una raíz cuadrada de\(z\) es\(\sqrt{r}e^{i\theta/2}\text{.}\) Otra raíz cuadrada de\(z\) es lo negativo de esa expresión. Cualquier otra raíz cuadrada de\(z\) tendría que tener norma\(\sqrt{|z|}\) y argumento\(\theta/2\) más o menos un múltiplo entero de\(\pi\text{,}\) por lo que estas deben ser todas las raíces cuadradas de\(z\text{.}\)

Ejercicio 9

Encuentra todas las soluciones complejas de las siguientes ecuaciones.

a.\(\displaystyle \displaystyle z^2 + 3z + 5 = 0\)

b.\(\displaystyle (z - i)(z + i) = 1\)

c.\(\displaystyle \displaystyle \frac{2z + i}{-z+3i} = z\)

Responder

a.\(\displaystyle \displaystyle -\frac{3}{2} \pm i\frac{\sqrt{11}}{2}\)

b.\(\displaystyle 0\)

c.\(\displaystyle (1/2)[(-2 \pm 281^{1/4}\cos \varphi) + i(3 \pm 281^{1/4}\sin \varphi)]\text{,}\) donde

\(\varphi=(\arctan(16/5)+\pi)/2\)

Ejercicio 10

Utilice el hecho de que\(e^{ia}e^{ib}=e^{i(a+b)}\) junto con la fórmula de Euler\(e^{i\theta}=\cos\theta + i\sin\theta\) para derivar las fórmulas trigonométricas de suma de ángulos a continuación.

\ comenzar {alinear*}
\ cos (a+b) & =\ cos a\ cos b -\ sin a\ sin b\
\ sin (a+b) & =\ cos a\ sin b +\ sin a\ cos b
\ fin {alinear*}

Solución

Usando la fórmula de Euler para la primera igualdad a continuación, y luego usando la multiplicación compleja para la segunda igualdad, tenemos

\ begin {align}
e^ {ia} e^ {ib} & = (\ cos a + i\ sin a) (\ cos b + i\ sin b)\ notag\\
& = (\ cos a\ cos b -\ sin a\ sin b) + i (\ cos a\ sin b +\ sin a\ cos b). \ label {localtag1}\ tag {\(\star\)}
\ end {align}

Por otro lado, la fórmula de Euler también da

\ comenzar {reunir}
e^ {i (a+b)} =\ cos (a+b) + i\ sin
(a+b). \ label {localtag2}\ tag {\(\star\star\)}
\ end {reunir}

Equiparar partes reales e imaginarias de (⋆) y (⋆) da las identidades trigonométricas deseadas.

Ejercicio 11

Círculos y líneas.

a. para una variable real\(x\) y una constante real\(a\text{,}\) completar el cuadrado se refiere a reescribir la expresión de la\(x^2 - 2ax\) siguiente manera.

\ [
x^2-2ax = x^2-2ax +a^2 - a^2 =\ izquierda (x-a\ derecha) ^2
-a^2.
\ nonumber\]

Una versión compleja de completar el cuadrado para una variable compleja z y una constante compleja a es la siguiente.

\ [
|z|^2-2re (za^\ ast) =|z-a|^2
-|a|^2\ label {complexcompletesquare}\ tag {1.1.24}
\]

Escribir una derivación para justificar esto. Luego usa completar el cuadrado para encontrar el centro y el radio del círculo dado por la ecuación\(|z|^2 -iz +iz^\ast -5=0\text{.}\)

b. escribir una prueba alternativa para la forma general para la ecuación de una línea (1.1.23), de la siguiente manera. Vamos\(a=u+iv\text{,}\)\(b=r+is\text{,}\)\(z=x+iy\text{.}\) Encuentra la ecuación de la línea\(Im(az+b)=0\) en términos de las variables reales\(x,y\) y constantes reales\(u,v,r,s\text{.}\) Explique por qué es necesario que\(a\neq 0\text{.}\)

Ejercicio 12

Números complejos como matrices reales 2×2.

Vamos\({\mathcal M}_\mathbb{C}\) denotar el conjunto de matrices 2×2 de la forma\(\left[\begin{array}{cc}a& b\\-b& a\end{array}\right]\) con\(a,b\in \mathbb{R}\text{.}\) Dado un número complejo\(z\) con forma cartesiana\(z=a+bi\text{,}\) vamos a\(M(z)\) denotar la matriz en\ (\ left [\ begin {array} {cc} a &
b\\ -b& a\ end {array}\ right]\) in\({\mathcal M}_\mathbb{C}\text{.}\) Inversamente, dada una matriz \(M\in {\mathcal M}_\mathbb{C}\)con entrada superior izquierda\(a\) y entrada superior derecha\(b\text{,}\) permiten\(C(M)\) denotar el número complejo\(a+bi\text{.}\) Es claro que las asignaciones\(z\to M(z)\) y\(M\to C(M)\) son inversas entre sí, y establecer una correspondencia uno a uno\(\mathbb{C}\leftrightarrow {\mathcal M}_\mathbb{C}\text{.}\)

a. Espectáculo que\({\mathcal M}_\mathbb{C}\) se cierra bajo suma y multiplicación. Es decir, supongamos que\(M,N\) son elementos de\({\mathcal M}_\mathbb{C}\text{.}\) Mostrar eso\(M+N\) y también\(MN\) son elementos de\({\mathcal M}_\mathbb{C}\text{.}\)

b. Demostrar que la suma compleja y la multiplicación se “reflejan” en Es\({\mathcal M}_\mathbb{C}\text{.}\) decir, mostrar eso\(C(M(z)+M(w))=z+w\) y\(C(M(z)M(w))=zw\) para todos\(z,w\in \mathbb{C}\text{.}\)