1.4: Relaciones de equivalencia

Definiciones

Una relación en un conjunto\(X\) es un subconjunto de\(X\times X\text{.}\) Dada una relación\(R\subseteq X\times X\text{,}\) que escribimos\(x\sim_R y\text{,}\) o simplemente\(\) x~y si\(\) R se entiende por contexto, para denotar eso\(\). (x, y) R. Una relación es reflexiva si\(\) x~x por cada\(\) x en\(\) .X. Una relación es simétrica si\(x\sim y\) implica\(y\sim x\text{.}\) Una relación es transitiva si\(x\sim y\) y\(y\sim z\) juntos implican que\(x\sim z\text{.}\) Una relación se denomina relación de equivalencia si es reflexiva, simétrica y transitiva. Dada una relación de equivalencia sobre\(X\) y un elemento\(x\in X\text{,}\) que escribimos\([x]\) para denotar el conjunto

\ [
[x] =\ {y\ en X\ dos puntos x\ sim y\},\ etiqueta {equivalenciaclase}\ etiqueta {1.4.1}
\]

llamada la clase de equivalencia del elemento\(x\text{.}\) El conjunto de clases de equivalencia se denota es\(X/\!\!\sim\text{,}\) decir,

\ [
X/\! \! \ sim\; =\ {[x]\ dos puntos x\ en X\}. \ label {setofequivclasses}\ tag {1.4.2}
\]

Una partición de un conjunto\(X\) es una colección de conjuntos disjuntos no vacíos cuya unión es\(X\text{.}\)

Hechos

Hecho 1.4.1. Relaciones de equivalencia y particiones.

\(X\)Déjese ser un conjunto. Las relaciones de equivalencia sobre\(X\) y las particiones de\(X\) están en correspondencia uno a uno, de la siguiente manera. Dada una relación de equivalencia\(∼\) en\(X\text{,}\) la colección

\ [
X/\! \! \ sim\; =\ {[x]\ dos puntos x\ en X\}
\ nonumber\]

es una partición de\(X\text{.}\) Por el contrario, dada una partición\({\mathcal P}\) de\(X\text{,}\) la relación\(\sim_{\mathcal P}\) definida por

\ [
x\ sim_ {\ mathcal P} y\ Leftrightarrow x, y\ text {mienten en el mismo elemento de} {\ mathcal P}
\ nonumber\]

es una relación de equivalencia. Estas correspondencias son inversas entre sí. Es decir,\(\sim = \sim_{(X/\sim)}\) y\(X/(\sim_{\mathcal P}) = {\mathcal P}\text{.}\)

Hecho 1.4.2. Construcción de funciones sobre conjuntos de clases de equivalencia.

Dejar\(∼\) ser una relación de equivalencia en un conjunto\(X\text{,}\) let\(\pi\colon X\to X/\!\!\sim\) denotar el mapa dado por\(x\to [x]\text{,}\) y let\(f\colon X\to Y\) ser una función. Existe un mapa\(\overline{f}\colon X/\!\!\sim \to Y\) tal que\((\overline{f}\circ \pi)(x)=f(x)\) para todos\(x\in X\) si y solo si\(f\) es constante en clases de equivalencia (es decir, si y solo si\([x\sim y\Rightarrow f(x)=f(y)]\text{.}\)

Nota sobre terminología: cuando una función\(f\) es constante en clases de equivalencia, decimos que la función asociada\(\overline{f}\) está bien definida.

Hecho 1.4.3. Construcción de relaciones de equivalencia y particiones a partir de funciones.

Dada una función\(f\colon X\to Y\text{,}\) hay una relación de equivalencia natural\(\sim_f\) en\(X\) dada por\(x\sim_f y\) si y solo si\(f(x)=f(y)\text{.}\) El conjunto correspondiente de clases de equivalencia es\(X/\!\!\sim_f \; = \{f^{-1}(y)\colon y\in f(X)\}\text{.}\) Además, la función\(X/\!\!\sim_f \; \to f(X)\) dada por\([x]\to f(x)\) es una correspondencia uno a uno.

Ejemplo importante: los enteros módulo un entero n

Dejar\(n\) ser un entero positivo. \(\sim_n\)Sea la relación sobre los enteros\(\mathbb{Z}\) dada por

\ [
x\ sim_n y\ Leftrightarrow n| (x-y)
\ nonumber\]

(recuerde que los símbolos "\(a|b\)" para enteros\(a,b\text{,}\) pronunciados "\(a\)divide\(b\) “, significa\(b=ka\) para algún entero\(k\)). Es fácil demostrar que\(\sim_n\) es una relación de equivalencia, y que las clases de equivalencia son precisamente el conjunto

\ [
Z/\! \! \ sim_n =\ {[0], [1], [2],\ ldots, [n-1]\}.
\ nonumber\]

Punto de control 1.4.4.

1. Verificar que la relación\(\sim_n\) sea efectivamente una relación de equivalencia.

2. Verificar que las clases de equivalencia de la relación de equivalencia\(\sim_n\) son de hecho\(\{[0],[1],[2],\ldots,[n-1]\}\text{.}\) Pista: Utilice el algoritmo de división, que dice que para cualquiera\(x\in \mathbb{Z}\text{,}\) hay enteros únicos\(q,r\text{,}\) con\(r \) en el rango\(0\leq r\leq n-1\text{,}\) tal que\(x=qn+r\text{.}\)

 

Este conjunto de clases de equivalencia es fundamental y omnipresente en matemáticas. En lugar de escribir\(Z/\!\!\sim_n\text{,}\) la notación universalmente utilizada es\(\mathbb{Z}_n\text{.}\) En lugar de escribir\(x\sim_n y\text{,}\) la notación universalmente utilizada es\(x=y\pmod{n}\) (o a veces\(x\equiv y\pmod{n}\)).

Una herramienta útil: diagramas conmutativos

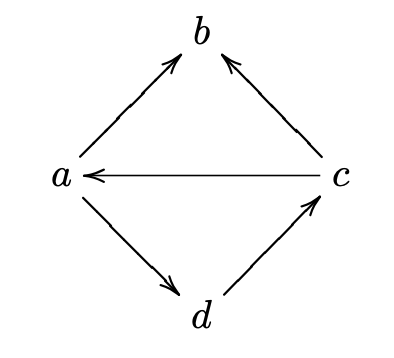
Una gráfica dirigida (o dígrafo) es un conjunto\(V\) de vértices y un conjunto\(E\subset V\times V\) de aristas dirigidas. Dibujamos imágenes de dígrafos dibujando una flecha apuntando de un vértice\(v\) a un vértice\(w\) cada vez que\((v,w)\in E\text{.}\) Ver Figura 1.4.5.

Un camino en una gráfica dirigida es una secuencia de vértices\(v_0,v_2,\ldots,v_{n}\) tal que\((v_{i-1},v_i)\in E\) para\(1\leq i\leq n\text{.}\) El vértice\(v_0\) se llama el vértice inicial y\(v_n\) se llama el vértice final de la ruta\(v_0,v_2,\ldots,v_{n}\text{.}\)

Figura 1.4.5. Ejemplo de una gráfica dirigida con conjunto de vértices\(V=\{a,b,c,d\}\) y conjunto\(E=\{(a,b),(c,b),(c,a),(a,d),(d,c)\text{.}\) de bordes Las secuencias de vértices\(c,b\) y\(c,a,b\) son ambas rutas desde\(c\) hasta\(b\text{.}\)

Un diagrama conmutativo es una gráfica dirigida con dos propiedades.

1. Los vértices están etiquetados por conjuntos y los bordes dirigidos están etiquetados por funciones entre esos conjuntos. Es decir, el borde dirigido\(f=(X,Y)\) denota una función\ (f\ dos puntos
   X\ a Y\ text {.}\)
2. Siempre que hay dos caminos desde un vértice inicial\(X\) hasta un vértice final,\(Y\text{,}\) la composición de las funciones a lo largo de una ruta es igual a la composición de las funciones a lo largo de la otra ruta. Es decir, si\(X_0,X_1,\ldots,X_n\) es un trazado con aristas\(f_i\colon X_{i-1}\to X_{i}\) para\(1\leq i\leq n\) y\(X_0=Y_0,Y_1,Y_2,\ldots,Y_m=X_n\) es un trazado con aristas\(1\leq i\leq m\text{,}\) para\(1\leq i\leq m\text{,}\) entonces

   \ [
   f_n\ circ f_ {n-1}\ circ\ cdots\ circ f_1=g_m\ circ
   g_ {m-1}\ circ\ cdots\ circ g_1.
   \ nonumber\]

La Figura 1.4.6 muestra un diagrama conmutativo que va con el hecho 1.4.2.

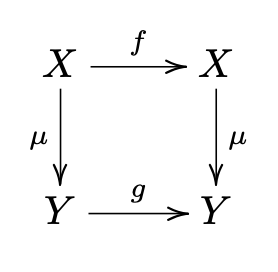
La Figura 1.4.7 muestra un diagrama conmutativo que ilustra la definición de transformaciones conjugadas.

Figura 1.4.6. Un diagrama conmutativo que muestra la relación\(\overline{f}\circ \pi = f\) en Fact 1.4.2.

Figura 1.4.7. Un diagrama conmutativo que ilustra la definición de transformaciones conjugadas\(f,g\) dada en el Grupo de Ejercicio 1.3.3.3—6.

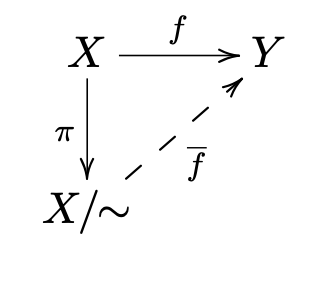
Ejercicios

Los enteros módulo\(n\text{.}\) Let n ser un entero positivo.

Ejercicio 1

Sea ω el número complejo\(\omega=e^{2\pi i/n}\text{,}\) y\(f\colon \mathbb{Z}\to \mathbb{C}\) déjese dar por\(m\to \omega^m\text{.}\) Mostrar que la relación de equivalencia\(\sim_f\) dada por el hecho 1.4.3 es la misma que\(\sim_n\text{.}\)

Ejercicio 2

Demostrar que la operación de adición en\(\mathbb{Z}_n\) dada por

\ [
[x] + [y] := [x+y]
\ nonumber\]

está bien definido. Esto significa mostrar que si\([x]=[x']\) y\([y]=[y']\text{,}\) entonces\([x+y]=[x'+y']\text{.}\)

Ejercicio 3

Demostrar que la operación de multiplicación en\(\mathbb{Z}_n\) dada por

\ [
[x]\ cdot [y] := [xy]
\ nonumber\]

está bien definido.

Ejercicio 4

Construcción alternativa de\(\mathbb{Z}_n\) Otra definición estándar del conjunto\(\mathbb{Z}_n\), junto con sus operaciones de suma y multiplicación, es la siguiente. Dado un entero\(a\text{,}\) escribimos\(a MOD n\) para denotar el resto obtenido al dividir\(a\) por\(n\) (el entero\(a MOD n\) es el mismo que el entero\(r\) en la sentencia del algoritmo de división dado en Checkpoint 1.4.4 ). Ahora define\(\mathbb{Z}_n\) para ser el conjunto

\ [
\ mathbb {Z} _n=\ {0,1,2,\ ldots, n-1\},
\ nonumber\]

definir la operación de adición\(+_n\)\(\mathbb{Z}_n\) en

\ [
x+_n y= (x+y) MOD n
\ nonumber\]

y definir la operación\(\cdot_n\) de multiplicación\(\mathbb{Z}_n\) por

\ [
x\ cdot_n y = (xy) MOD n.
\ nonumber\]

Mostrar que esta versión de\(\mathbb{Z}_n\) es equivalente a la versión desarrollada en Ejercicio 1.4.5.2 y Ejercicio 1.4.5.3.

Ejercicio 5

Ejemplos de diagramas conmutativos.

1. Dibuja un diagrama conmutativo que ilustre los resultados del Ejercicio 1.3.3.5.
2. La ley distributiva para\(\mathbb{Z}_n\) dice que

   \ [
   [x]\ izquierda ([y] + [z]\ derecha) = [x] [y] +
   [x] [z]
   \ nonúmero\]

   para todos\([x],[y],[z]\in \mathbb{Z}_n\text{.}\) Etiquete los mapas en el diagrama conmutativo a continuación para expresar la ley distributiva.

   

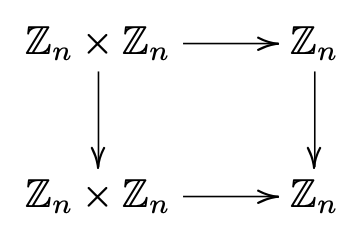
   Figura 1.4.8.

Ejercicio 6

Demostrar Hecho 1.4.1.

Ejercicio 7

Demostrar Hecho 1.4.2.

Ejercicio 8

Demostrar Hecho 1.4.3.