2.1: Ejemplos de grupos
- Page ID
- 115623
Los grupos son uno de los objetos algebraicos más básicos, pero tienen una estructura lo suficientemente rica como para ser ampliamente útiles en todas las ramas de las matemáticas y sus aplicaciones. Un grupo es un conjunto\(G\) con una operación binaria\(G\times G \to G\) que tiene una lista corta de propiedades específicas. Antes de dar la definición completa de un grupo en la siguiente sección (ver Definición 2.2.1), esta sección introduce ejemplos de algunos grupos importantes y útiles.
Permutaciones
Una permutación de un conjunto\(X\) es una biyección de\(X\) a sí misma, es decir, una función que es a la vez uno-a-uno y sobre. Dadas dos permutaciones\(\alpha,\beta\) de un conjunto\(X\text{,}\) escribimos\(\alpha\beta\) para denotar la composición de funciones\(\alpha\circ\beta\text{.}\)
Dejar\(X\) ser un conjunto y dejar\(Perm(X)\) denotar el conjunto de todas las permutaciones de\(X\text{.}\) El grupo de permutaciones de\(X\) es el conjunto\(G=Perm(X)\) junto con la operación binaria\(G\times G\to G\) dada por la composición de la función, es decir,\((\alpha,\beta) \to \alpha\circ\beta\text{.}\) Para el caso especial\(X = \{1,2,\ldots,n\}\) para algún entero\(n\geq 1\text{,}\) el grupo\(Perm(X)\) se llama el grupo simétrico, y se denota\(S_n\text{.}\)
- Punto de control 2.1.2.
-
Una permutación σ de\(X=\{1,2,\ldots,n\}\) puede especificarse mediante una lista de valores\([\sigma(1),\sigma(2),\ldots,\sigma(n)]\text{.}\) 1 Por ejemplo, la lista\([3,1,2]\) especifica la permutación\(\sigma\colon \{1,2,3\}\to\{1,2,3\}\) dada por
\ [
\ sigma (1) =3,\;\ sigma (2) =1,\;\ sigma (3) =2.
\ nonumber\]Let\(\tau=[2,1,3]\text{.}\) Find\(\sigma\tau\text{,}\)\(\tau\sigma\text{,}\) y\(\sigma^2=\sigma\sigma\text{.}\)
Contestar
\(\sigma\tau= [1,3,2]\text{,}\)\(\tau\sigma=[3,2,1]\text{,}\)\(\sigma^2=[2,3,1]\)
Simetrías de polígonos regulares
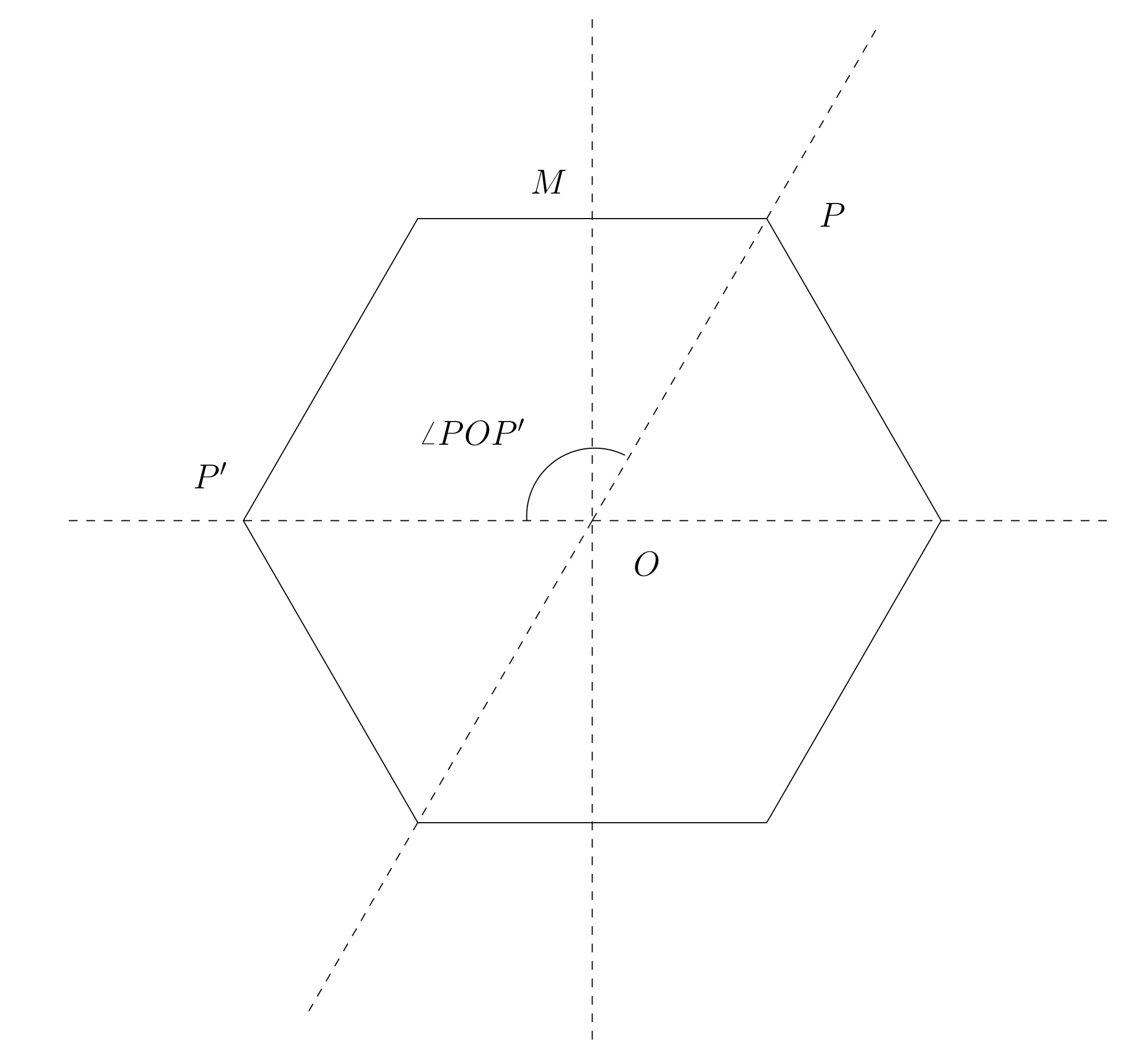
Informalmente e intuitivamente, decimos que los polígonos regulares tienen simetrías rotacionales y especulares. Específicamente, las simetrías rotacionales son rotaciones alrededor del centro\(O\) del polígono, en sentido horario o antihorario, por algún ángulo\(\angle POP'\text{,}\) donde\(P,P'\) se encuentran dos vértices cualesquiera. Las simetrías especulares del polígono son reflejos a través de líneas de la forma\(\overline{OP}\) o\(\overline{OM}\text{,}\) donde\(P\) está cualquier vértice y\(M\) es el punto medio de cualquier borde del polígono. Ver Figura 2.1.3.
Aquí hay algunas notaciones estándar para rotaciones y reflexiones en el plano. Ver Figura 2.1.4.
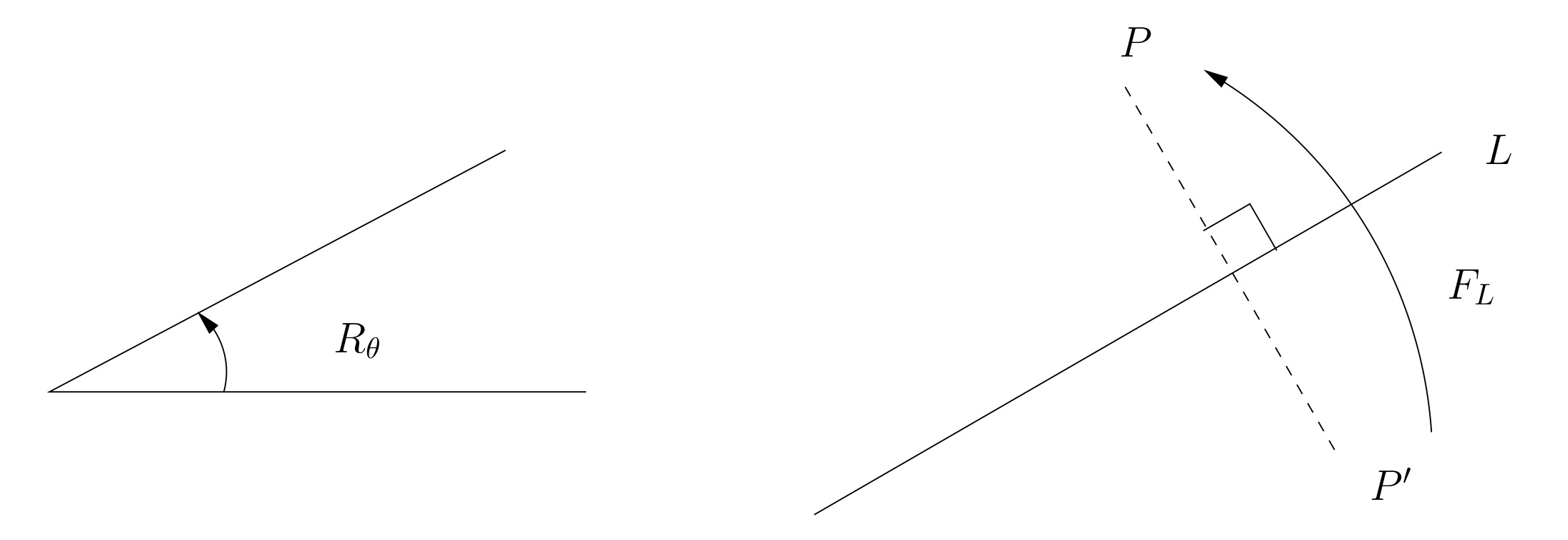
Rotaciones en el avión.
Fijar un punto central\(O\text{.}\) Escribimos\(R_\theta\) para denotar la rotación por ángulo\(\theta\) alrededor del punto Las unidades de\(O\text{.}\) ángulo pueden ser revoluciones o grados o radianes, lo que sea más conveniente. Observamos la convención habitual de que los valores positivos\(\theta\) denotan rotaciones en sentido antihorario y los valores negativos\(\theta\) denotan rotaciones en sentido horario.
Reflexiones en el plano.
Escribimos\(F_L\) para denotar la reflexión a través de la línea\(L\text{.}\) Esto significa que\(P'=F_L(P)\) si y solo si\(\overline{PP'}\perp L\) y la distancia de\(P\) a\(L\) es la misma que la distancia de\(P'\) a\(L\text{.}\)
Dadas simetrías\(A,B\text{,}\) escribimos\(AB\)\(A\circ B\text{.}\) para denotar la composición Por ejemplo, para las simetrías del triángulo equilátero, con ángulos en grados, y con\(L=\overline{OP}\) para algún vértice\(P\text{,}\) tenemos\(R_{240}R_{120}=R_{0}\) y\(F_LR_{120}=R_{-120}F_L\text{.}\)
El grupo diedro, denotado\(D_n\) es el conjunto de simetrías de rotación y reflexión del\(n\) -gon regular junto con la operación binaria de composición de funciones.
- Punto de control 2.1.6.
-
Dejar\(X\) ser el cuadrado centrado en el origen en el\(x,y\) -plano con vértices en\((\pm 1,\pm 1)\text{.}\) El cuadrado\(X\) tiene líneas de simetría\(H,V,D,D'\) (horizontal, vertical, diagonal, y otra diagonal) donde\(H,V\) denotan los\(x,y\) ejes, respectivamente, y\(D,D'\) denotan las líneas \(y=-x,y=x\text{,}\)respectivamente. Ver Figura 2.1.7.
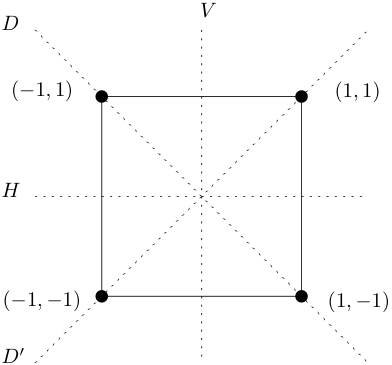
Figura 2.1.7. Líneas de simetría para el cuadrado. Las simetrías de la plaza\(X\) son
\ [
D_4=\ {R_0, R_ {1/4}, R_ {1/2}, R_ {3/4}, F_H, F_V, F_D, F_ {D'}\}
\ nonumber\]donde las unidades de ángulos de rotación son revoluciones. Encuentra lo siguiente.
- \(\displaystyle R_{1/4}R_{1/2}\)
- \(\displaystyle R_{1/4}F_H\)
- \(\displaystyle F_HR_{1/4}\)
- \(\displaystyle F_HF_D\)
- \(\displaystyle F_DF_H\)
- \(\displaystyle (F_DR_{1/2})^2= F_DR_{1/2}F_DR_{1/2}\)
- \(\displaystyle (F_DR_{1/2})^3\)
Contestar
- \(\displaystyle R_{3/4}\)
- \(\displaystyle F_{D'}\)
- \(\displaystyle F_D\)
- \(\displaystyle R_{1/4}\)
- \(\displaystyle R_{3/4}\)
- \(\displaystyle R_0\)
- \(\displaystyle F_{D'}\)
Los números complejos de la norma 1
El grupo de círculo, denotado\(S^1\text{,}\) es el conjunto
\ [
S^1=\ {z\ in\ mathbb {C}\ dos puntos |z|=1\}
\ nonúmero\]
de números\(1\) complejos de norma junto con la operación binaria\(S^1\times S^1\to S^2\) dada por la multiplicación compleja, es decir,\((z,w)\to zw\text{.}\)
- Punto de control 2.1.9.
-
Demostrar que si\(z,w\) son elementos de\(S^1\text{,}\) entonces su producto también\(zw\) está en\(S^1\text{.}\)
Las raíces n-ésimas de la unidad
Dejar\(n\geq 1\) ser un entero. El conjunto
\ [
C_n=\ {z\ in\ mathbb {C}\ dos puntos
z^n=1\}
\ nonúmero\]
se llama el conjunto de raíces (complejas)\(n\) -ésima de la unidad.
- Punto de control 2.1.10.
-
1. Vamos\(\omega=e^{i2\pi/n}\text{.}\) Mostrar que\(\omega^k\) está en\(C_n\) para todos los enteros\(k\text{.}\)
2. Mostrar que, si\(z\) es un elemento de\(C_n\text{,}\) entonces\(z=\omega^k\) para algún entero\(k\text{.}\)
3. Demostrar que el conjunto\(C_n\) consiste precisamente en los\(n\) elementos
\ [
\ {\ omega^0,\ omega^1,\ omega^2,\ lpuntos,\ omega^ {n-1}\}.
\ nonumber\]
El conjunto\(C_n=\{\omega^0,\omega^1,\omega^2,\ldots,\omega^{n-1}\}\), junto con la operación de multiplicación compleja, se llama el grupo de\(n\) -ésimo raíces de la unidad.
Enteros
El conjunto\(\mathbb{Z}\) de enteros, junto con la operación de suma, se denomina grupo de enteros. De igual manera, el conjunto\(\mathbb{Z}_n\) de enteros módulo\(n\) (donde\(n\) es algún entero\(n\geq 1\)), junto con la operación de módulo de suma\(n\text{,}\) se llama el grupo de enteros mod\(n\).
Matrices invertibles
Dejar\(n\geq 1\) ser un entero. Escribimos\(GL(n,\mathbb{R})\) para denotar el conjunto de matrices\(n\times n\) invertibles con entradas reales. Escribimos\(GL(n,\mathbb{C})\) para denotar el conjunto de matrices\(n\times n\) invertibles con entradas complejas.
El conjunto\(GL(n,\mathbb{R})\) (respectivamente\(GL(n,\mathbb{C})\), junto con la operación binaria de multiplicación matricial, se denomina grupo de matrices invertibles\(n×n\) reales (respectivamente, complejas), o también grupo lineal general
Elementos distintos de cero en un campo
\(\mathbb{F}\)Sea un campo, como los números racionales\(\mathbb{Q}\), los números\(\mathbb{R}\) reales o los números complejos\(\mathbb{C}\). Escribimos\(\mathbb{F}^\ast\) para denotar el conjunto de elementos distintos de cero en\(\mathbb{F}\).
\(\mathbb{F}\)Déjese ser un campo. El conjunto\(\mathbb{F}^\ast\), junto con la operación binaria de multiplicación, se denomina grupo de elementos distintos de cero en el campo\(\mathbb{F}\).
Cuaterniones unitarios
El conjunto\(U(\mathbb{H})\) de cuaterniones de norma\(1\) (definido en la Subsección 1.2.4), junto con la operación binaria de multiplicación de cuaterniones, se denomina grupo de cuaterniones unitarios.
Ejercicios
Matrices para el grupo diedro D4. Dejar\(H\) denotar el\(x\) eje -en el\(x,y\) plano. El mapa\(F_H\colon \mathbb{R}^2\to \mathbb{R}^2\) es un mapa lineal cuya matriz es\ (\ displaystyle\ left [\ begin {array} {cc} 1 & 0\\ 0 &
-1\ end {array}\ right]\ text {.}\) El mapa\(R_{1/4}\colon \mathbb{R}^2\to \mathbb{R}^2\) es un mapa lineal cuya matriz es\ (\ displaystyle\ left [\ begin {array} {cc} 0 & -1\\ 1 &
0\ end {array}\ right]\ text {.}\) Encuentre las matrices para los elementos restantes del grupo diedro\(D_4\) como se especifica en Checkpoint 2.1.6.
Operaciones de números complejos para el grupo diedro\(D_4\). Dejar\(H\) denotar la línea real\(\mathbb{R}\) en el plano complejo\(\mathbb{C}\text{.}\) El mapa\(F_H\colon \mathbb{C}\to \mathbb{C}\) es conjugación compleja\(z\to {z}^\ast\text{.}\) El mapa\(R_{1/4}\colon \mathbb{C}\to \mathbb{C}\) es el mapa\(z\to e^{i\pi/2}z=iz\text{.}\) Encuentra los mapas\(\mathbb{C}\to \mathbb{C}\) para los elementos restantes del grupo diedro\(D_4\) como se especifica en Checkpoint 2. 1.6.
Recordemos que una operación binaria\ ((x, y)
\ a x\ ast y\) es conmutativa si\ (x\ ast
y=y\ ast x\) para todos los valores posibles de\(x,y\text{.}\)
- ¿Cuáles de las operaciones grupales en los ejemplos de esta sección son conmutativas? ¿Cuáles no son?
- Demostrar que no\(S_n\) es conmutativo para\(n\gt 2\text{.}\)
Una de las propiedades de un grupo es la existencia de un elemento de identidad. Se trata de un elemento de grupo e con la propiedad que\(eg=ge=g\) para cada uno\( g\) en\(G\text{.}\) Encuentra un elemento de identidad para cada uno de los grupos en los ejemplos de esta sección.
Una de las propiedades de un grupo es la existencia de un elemento inverso para cada elemento del grupo. Esto quiere decir que para cada uno\(g\) de un grupo\(G\text{,}\) hay un elemento\(h\) con la propiedad que\(gh=hg=e\text{,}\) donde\(e\) está el elemento de identidad del grupo. Encuentra inversos para la siguiente lista de elementos de grupo.
- \([4,2,1,3]\)en\(S_4\)
- \(R_{120}\)en\(D_6\) (donde\(120\) está en grados)
- \(\frac{1}{\sqrt{2}}(-1+i)\)en\(S^1\)
- \(7\)en\(\mathbb{Z}\)
- \(7\)en\(\mathbb{Z}_9\)
- \(\displaystyle \left[\begin{array}{cc}1 & 2\\ 2 & 1\end{array}\right]\)en\(GL(2,\mathbb{R})\)
- \(r=a+bi+cj+dk\)en\(U(\mathbb{H})\)


