3.2: Geometría Möbius

La geometría de Möbius proporciona un marco unificador para el estudio de geometrías planas. En particular, los grupos de transformación de geometrías hiperbólicas y elípticas en las secciones que siguen son subgrupos del grupo de transformaciones de Möbius.

Transformaciones de Möbius

Una transformación de Möbius (también llamada transformación fraccionaria lineal) del plano complejo extendido\(\hat{\mathbb{C}}\) es una función de la forma

\ begin {ecuación}
f (z) =\ frac {az+b} {cz+d}\ label {stdlinfractransf}\ tag {3.2.1}
\ end {ecuación}

donde\(z\) es una variable compleja,\(a,b,c,d\) son constantes complejas, y\(ad-bc\neq 0\text{.}\) para completar la definición, hacemos las asignaciones\(f(-d/c)=\infty\) y\(f(\infty)=a/c\) si\(c\neq 0\text{.}\) si\(c=0\text{,}\) asignamos\(f(\infty)=\infty\text{.}\)

Nota sobre convención notacional: Se acostumbra utilizar letras mayúsculas como\(S,T,U\) para denotar transformaciones de Möbius. También es costumbre omitir los paréntesis, y escribir\(Tz\) en lugar de\(T(z)\) denotar el valor de una transformación de Möbius.

Punto de control 3.2.1.

Dejar\(f(x)=(ax+b)/(cx+d)\) ser una función de una variable real\(x\) con constantes reales\(a,b,c,d\) con\(ad-bc\neq 0\) y\(c\neq 0\text{.}\)

1. Demostrar que\(\displaystyle \lim_{x\to -d/c}|f(x)|=\infty\text{.}\)
2. Demostrar que\(\displaystyle \lim_{x\to \infty}f(x)=a/c\text{.}\)

Punto de control 3.2.2.

Demostrar que la condición\(ad-bc\neq 0\) es necesaria y suficiente para la invertibilidad. Encuentra una fórmula para la inversa de\(z\to (az+b)/(cz+d)\text{.}\)

Punto de control 3.2.3.

Mostrar que la composición de dos transformaciones de Möbius es una transformación de Möbius. Sugerencia: Primero mostrar que la composición tiene la forma\(z\to \frac{rz+s}{tz+u}\text{.}\) Siguiente, en lugar de un cálculo de fuerza bruta para verificar que\(ru-ts\neq 0\text{,}\) use Checkpoint 3.2.2.

Definición 3.2.4.

El conjunto de todas las transformaciones de Möbius forma un grupo\(\mathbf{M}\text{,}\) llamado el grupo Möbius, bajo la operación de composición de funciones. La geometría de Möbius es el par\((\hat{\mathbb{C}},\mathbf{M})\text{.}\)

Existe una relación natural entre las operaciones del grupo Möbius y las operaciones de grupos matriciales. El mapa\ ({\ mathcal T}\ colon
GL (2,\ mathbb {C})\ a\ mathbf {M}\) ser dado por

\ begin {ecuación}
\ left [
\ begin {array} {cc} a& b\\ c& d\ end {array}\ right]\ to
\ left [z\ to\ frac {az+b} {cz+d}\ right]\ label {gl2tomobgp}\ tag {3.2.2}
\ end {ecuación}

es un homomorfismo grupal. El núcleo de\({\mathcal T}\) es el grupo de matrices escalares distintas de cero.

\ begin {ecuación*}
\ ker {\ mathcal T} =\ left\ {\ left [
\ begin {array} {cc} k& 0\\ 0& k\ end {array}\ right],
k\ neq 0\ right\}\ text {.}
\ end {ecuación*}

El grupo cociente\(GL(2,\mathbb{C})/\ker{\mathcal T}\) se llama el grupo lineal proyectivo\(PGL(2,\mathbb{C})\text{.}\) Así tenemos un grupo isomorfismo

\ begin {ecuación*}
PGL (2,\ mathbb {C})\ approx\ mathbf {M}\ texto {.}
\ end {ecuación*}

Punto de control 3.2.5.

Mostrar que el mapa\({\mathcal T}\) es un homomorfismo grupal. Demostrar que el núcleo de\({\mathcal T}\) es

\ begin {ecuación*}
\ ker {\ mathcal T} =\ left\ {\ left [
\ begin {array} {cc} k& 0\\ 0& k\ end {array}\ right],
k\ neq 0\ right\}\ text {.}
\ end {ecuación*}

Homotedades, rotaciones, traducciones e inversiones (ver Cuadro 3.1.4 en la Sección 3.1) son casos especiales de transformaciones de Möbius. Estas transformaciones básicas pueden verse como bloques de construcción para transformaciones generales de Möbius, de la siguiente manera.

Proposición 3.2.6.

Cada transformación de Möbius es una composición de homotedades, rotaciones, traducciones e inversiones.

Prueba.

Ver Ejercicio 3.2.6.1

Punto de control 3.2.7.

1. Identificar los valores de los coeficientes\(a,b,c,d\) en una transformación de Möbius\(z\to \frac{az+b}{cz+d}\) que es homothety, rotación, traslación e inversión, respectivamente.
2. Escribe una transformación de Möbius que haga “rotación en sentido horario por un cuarto de rotación alrededor del punto\(2-i\)”.

Corolario 3.2.8.

Las transformaciones de Möbius son conformes.

Prueba.

Aplicar la Proposición 3.2.6 y el Grupo de Ejercicios 3.1.4.2—5.

A continuación, una simple observación, en forma del siguiente Lema, conduce a un resultado llamado Teorema Fundamental de la Geometría Möbius.

Lema 3.2.9.

Si una transformación de Möbius tiene más de dos puntos fijos, entonces es la transformación de identidad.

Prueba.

Pista: solo resuelve\(z=\frac{az+b}{cz+d}\text{.}\) Tendrás que considerar casos.

Proposición 3.2.10. El teorema fundamental de la geometría de Möbius.

Una transformación de Möbius está completamente determinada por tres pares de entrada-salida cualquiera. Esto significa que para cualquier triple de valores de entrada distintos\(z_1,z_2,z_3\) en\(\hat{\mathbb{C}}\) y cualquier triple de valores de salida distintos\(w_1,w_2,w_3\) en\(\hat{\mathbb{C}}\text{,}\) hay un único\(T\in \mathbf{M}\) tal que\(Tz_i=w_i\) para\(i=1,2,3\text{.}\)

Prueba.

Esquema: Supongamos que hay dos transformaciones de este tipo,\(S\) y\(T\text{.}\) Mostrar que\ (S\ circ
T^ {-1}\) corrige tres puntos. Ahora aplica el Lema anterior.

Relación cruzada

En lo que sigue, consideramos el caso especial del triple de salida\(w_1=1\text{,}\)\(w_2=0\text{,}\)\(w_3=\infty\text{.}\) Dado tres puntos distintos\(z_1,z_2,z_3\) en\(\hat{\mathbb{C}}\text{,}\) escribimos\((\cdot,z_1,z_2,z_3)\) para denotar la transformación única de Möbius que satisface\ (z_1\ a
1\ text {,}\)\(z_2\to 0\text{,}\) y\(z_3\to \infty\text{.}\) escribimos \((z_0,z_1,z_2,z_3)\)para denotar la imagen de\(z_0\) bajo\((\cdot,z_1,z_2,z_3)\text{.}\) La expresión\((z_0,z_1,z_2,z_3)\) se llama la relación cruzada de la\(4\) -tupla\(z_0,z_1,z_2,z_3\text{.}\) Las dos proposiciones siguientes dan importantes propiedades de relación cruzada.

Proposición 3.2.11. La relación cruzada es invariante.

Dejar\(z_1,z_2,z_3\) ser distintos puntos en\(\hat{\mathbb{C}}\text{,}\) let\(z_0\in \hat{\mathbb{C}}\text{,}\) y dejar\(T\) ser cualquier transformación de Möbius. Entonces tenemos

\ begin {ecuación*}
(z_0, z_1, z_2, z_3) = (Tz_0, Tz_1, Tz_2, Tz_3).
\ end {ecuación*}

Prueba.

Las transformaciones\((\cdot,z_1,z_2,z_3)\) y\((\cdot,Tz_1,Tz_2,Tz_3)\circ T\) ambas envían\(z_1\to 1\text{,}\)\(z_2\to 0\text{,}\) y\(z_3\to \infty\text{,}\) así deben ser iguales, por el Teorema Fundamental. Ahora aplica ambas transformaciones a\(z_0\text{.}\)

Proposición 3.2.12.

Dejar\(z_1,z_2,z_3\) ser distintos puntos en\(\hat{\mathbb{C}}\text{,}\) let\(T=(\cdot,z_1,z_2,z_3)\text{,}\) y dejar\(C_T=T^{-1}\left(\hat{\mathbb{R}}\right)\) ser la imagen inversa de la línea real extendida\(\hat{\mathbb{R}}=\mathbb{R}\cup \{\infty\}\) bajo\(T\text{.}\) Entonces\(C_T\) es un círculo euclidiano o línea recta. Además,\(C_T\) es el círculo euclidiano único o línea recta que contiene los puntos\(z_1,z_2,z_3\text{.}\)

Prueba.

Ver Ejercicio 3.2.6.4

Corolario 3.2.13.

La relación cruzada\((z_0,z_1,z_2,z_3)\) es real si y solo si se\(z_0,z_1,z_2,z_3\) encuentran sobre un círculo euclidiano o línea recta.

Corolario 3.2.14.

Deja entrar\(C\) un círculo euclidiano o una línea recta\(\hat{\mathbb{C}}\) y dejar que\(T\) sea cualquier transformación de Möbius. Entonces\(T(C)\) es un círculo euclidiano o línea recta.

Un círculo euclidiano o línea recta se llama clina (pronunciada “kline”) o círculo generalizado. Las proposiciones y corolarios anteriores muestran que el conjunto de todos los clinos es una sola clase de congruencia de figuras en geometría de Möbius.

Simetría con respecto a una clina

Geométricamente, el mapa de conjugación\(z\to z^{\ast}\) en el plano complejo es reflejo a través de la línea real. Esta simetría “espejo” generaliza a simetría con respecto a cualquier cline, de la siguiente manera. Dado un cline\(C\) que contiene\(z_1,z_2,z_3\) en\(\hat{\mathbb{C}}\text{,}\) let\(T=(\cdot,z_1,z_2,z_3)\text{.}\) Dado cualquier punto\(z\text{,}\) el punto simétrico con respecto a\(C\) es

\ begin {ecuación}
z^ {\ ast C} = (T^ {-1}\ circ conj\ circ T) (z)\ label {symmptdef}\ tag {3.2.3}
\ end {ecuación}

donde\(conj\colon \hat{\mathbb{C}}\to \hat{\mathbb{C}}\) está la extensión del mapa de conjugación al plano complejo extendido que envía\(\infty\to \infty^\ast=\infty\text{.}\) La idea es mapear\(C\) a la línea real vía\(T\text{,}\) luego conjugada, luego mapear la línea real de nuevo a\(C\text{.}\) Ver Figura 3.2.15.

Figura 3.2.15. Puntos simétricos\(z,z^{\ast C}\) con respecto al círculo\(C\)

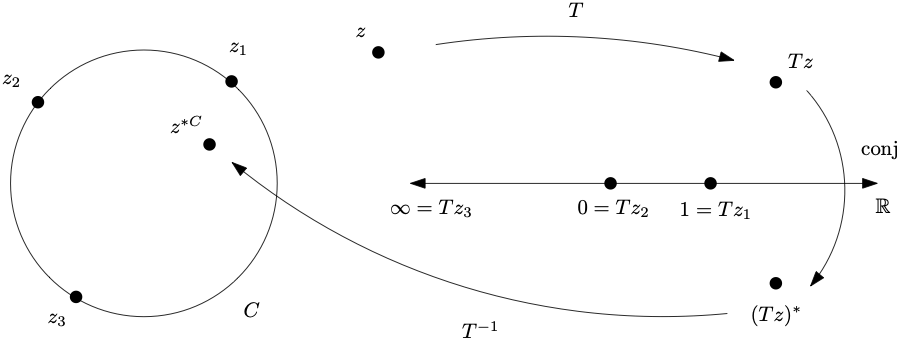
La definición de punto simétrico depende únicamente del círculo\(C\text{,}\) y no de los tres puntos\(z_1,z_2,z_3\text{.}\) Este hecho es corolario de la siguiente Proposición.

Proposición 3.2.16.

\(C\)Déjese ser un cline y\(S\) déjese ser una transformación Möbius. Si\(z,z'\) son un par de puntos que son simétricos con respecto a\(C\text{,}\) entonces\(Sz,Sz'\) son simétricos con respecto al cline Es\(S(C)\text{.}\) decir, tenemos

\ begin {ecuación*}
(Sz) ^ {\ ast S (C)} = S (z^ {\ ast C}).
\ end {ecuación*}

Prueba.

Dejen\(z_1,z_2,z_3\) ser tres puntos\(C\text{,}\) para que\(Sz_1,Sz_2,Sz_3\) sean tres puntos en\(S(C)\text{.}\) Let\(T=(\cdot,z_1,z_2,z_3)\) y let\(U=(\cdot,Sz_1,Sz_2,Sz_3)\text{.}\) Por invarianza de la relación cruzada, tenemos

\ begin {ecuación*}
(U\ circ S) z=tz\ text {.}
\ end {ecuación*}

Así tenemos

\ begin {align*}
(Sz) ^ {\ ast S (C)} & = (U^ {-1}\ circ conj\ circ
U) (Sz)\;\;\ text {(por definición)}\\
& = (S\ circ S^ {-1}\ circ U^ {-1}\ circ conj\ circ
U\ circ S) (z)\
& = S (S^ {-1}\ circ U^ {-1}\ circ conj\ circ
U\ circ S) (z)\\
& = S (T^ {-1}\ circ conj\ circ T) (z)\\
& = S (z^ {\ ast C})
\ end {alinear*}

según se desee.

Corolario 3.2.17.

La definición de\(z^{\ast C}\) depende únicamente del círculo\(C\text{,}\) y no de los tres puntos\(z_1,z_2,z_3\) utilizados en la definición (3.2.3).

Prueba.

Ver Ejercicio 3.2.6.6.

Formas normales

Concluimos esta sección sobre la geometría de Möbius con una discusión sobre la forma normal de una transformación de Möbius. Comenzamos con un Lema.

Lema 3.2.18.

Si una transformación de Möbius tiene exactamente dos puntos fijos\(0\) y\(\infty\text{,}\) luego tiene la forma\(z\to \alpha z\) para algunos no cero\ (\ alpha\ in
\ mathbb {C}\ text {.}\) Si una transformación de Möbius tiene un solo punto fijo en\(\infty\text{,}\) entonces tiene la forma\(z\to z+\beta\) para algunos distintos de cero\(\beta\in \mathbb{C}\text{.}\)

Prueba.

Ver Ejercicio 3.2.6.5.

Ahora supongamos que una transformación de Möbius\(T\) tiene dos puntos fijos,\(p\) y\(q\text{.}\) Let\(S\) be given by\(Sz = \frac{z-p}{z-q}\text{.}\) Let\(w=Sz\) and let\(U=S\circ T\circ S^{-1}\) be the transformation of the\(w\) -plane that is conjugada to\(T\) via\(S\) (ver Ejercicio Grupo 1. 3.3.3—6). Es fácil comprobar que\(U\) tiene exactamente dos puntos fijos\(0\) y\(\infty\text{.}\) Aplicando el Lema anterior, tenemos\(Uw=\alpha w\) para algunos no cero\ (\ alpha\ in
\ mathbb {C}\ text {.}\) Aplicando ambos lados de\(S\circ T=U\circ S\) a\(z\text{,}\) tenemos lo siguiente forma normal para\(T\text{.}\)

\ begin {ecuación}
\ frac {tz-p} {tz-q} =\ alfa
\ frac {z-p} {z-q}\ label {normalform2fixedpts}\ tag {3.2.4}
\ end {ecuación}

La transformación\(T\) se llama elíptica, hiperbólica o loxodérmica si\(U\) es una rotación\((|\alpha |=1)\), una homotez\((\alpha >0)\), o ninguna, respectivamente.

Por último, supongamos que una transformación de Möbius\(T\) tiene exactamente un punto fijo en\(p\text{.}\) Let\(S\) be given by\(Sz = \frac{1}{z-p}\text{.}\) Again, let\(w=Sz\) and let\(U=S\circ T\circ S^{-1}\text{.}\) Esta vez,\(U\) tiene exactamente un punto fijo en\(\infty\text{.}\) Aplicando el Lema, tenemos\(Uw=w+\beta\) para algunos no cero\ (\ beta \ in
\ mathbb {C}\ text {.}\) Aplicando ambos lados de\(S\circ T=U\circ S\) a\(z\text{,}\) tenemos la siguiente forma normal para\(T\text{.}\)

\ begin {ecuación}
\ frac {1} {tz-p} =
\ frac {1} {z-p} +\ beta\ label {normalformfixedpt}\ tag {3.2.5}
\ end {ecuación}

Una transformación de Möbius de este tipo se llama parabólica. A continuación se presenta un resumen de la terminología de clasificación asociada a las formas normales.

Cuadro 3.2.19. Resumen de formas normales de\(T\in \mathbf{M}\)

tipo de forma normal	forma normal	tipo de transformación conjugada
elíptica	\(\frac{Tz-p}{Tz-q}= \alpha \frac{z-p}{z-q}, |\alpha|=1\)	rotación
hiperbólico	\ (\ frac {tz-p} {tz-q} =\ alfa\ frac {z-p} {z-q}, \ alfa\ gt 0\)	homothety
loxodérmico	\ (\ frac {tz-p} {tz-q} =\ alfa\ frac {z-p} {z-q}, \ alfa\ neq 0\) \(|\alpha |\neq 1, \alpha\not\gt 0\)	composición de la homotez con rotación
parabólico	\ (\ frac {1} {tz-p} =\ frac {1} {z-p} +\ beta, \ beta\ neq 0\)	traducción

Círculos Steiner

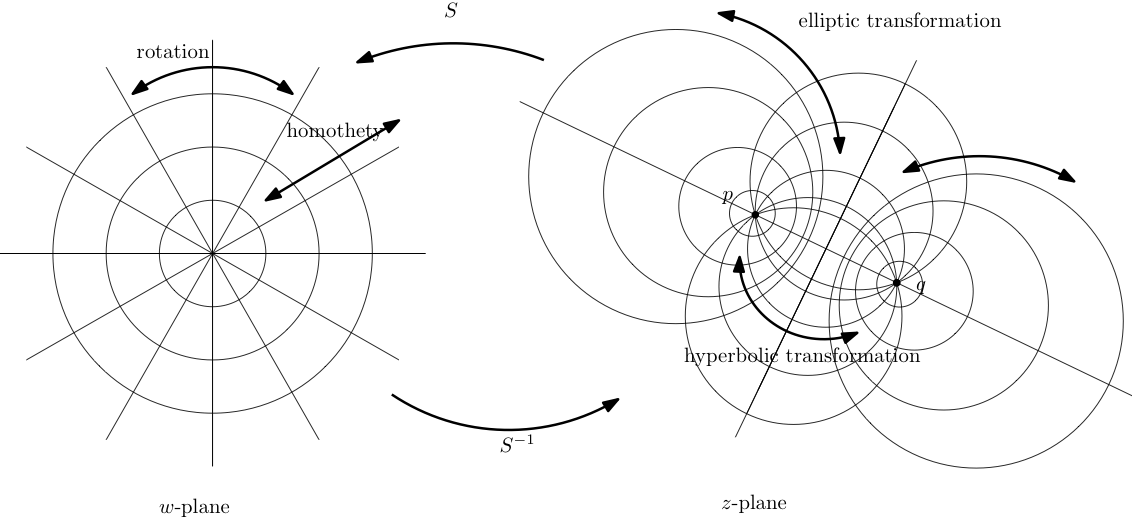
Figura 3.2.20. La rejilla de coordenadas polares y la cuadrícula de coordenadas circulares Steiner

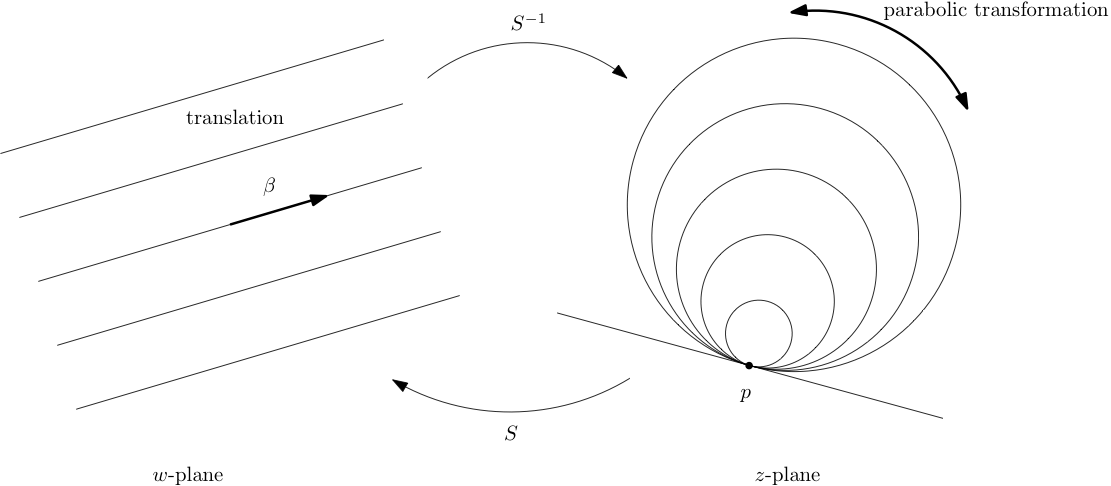
Figura 3.2.21. Líneas de rejilla de coordenadas degeneradas y círculos Steiner degenerados

La discusión de las formas normales muestra que cualquier transformación de Möbius sin identidad se conjuga con una de dos formas básicas,\(w\to \alpha w\) o\(w\to w+\beta\text{.}\) El sistema de coordenadas naturales para representar la acción de\ (w\ a
\ alpha w\) es coordenadas polares estándar. Ver Figura 3.2.20. Una homotez es un flujo a lo largo de líneas radiales y una rotación es un flujo alrededor de círculos polares. El sistema de coordenadas naturales “degeneradas” para representar una traducción\(w\to w+\beta\) es una familia de líneas paralelas a la línea que contiene el origen y\(\beta\text{.}\) A translation by\(\beta\) es un flujo a lo largo de estas líneas paralelas. Ver Figura 3.2.21.

Tirando de las cuadrículas de coordenadas polares y\(z\) degeneradas de vuelta al plano por\(S^{-1}\) cables a cuadrículas de coordenadas llamadas círculos de Steiner. ¹ En el caso donde\(T\) tiene dos puntos fijos\(p,q\text{,}\) el mapa de conjugación\(Sz=\frac{z-p}{z-q}\) toma\(p\to 0\text{,}\)\(q\to \infty\text{.}\) Por lo tanto\(S^{-1}\) mapas\(0\to p\) y\(\infty \to q\text{.}\) La transformación\(S^{-1}\) mapea líneas radiales en el plano w a clines en el \(z\)-plano que contiene\(p\) y\(q\) llama círculos Steiner del primer tipo y\(S^{-1}\) mapea círculos polares en el\(w\) -plano a clines en el\(z\) -plano llamados círculos Steiner del segundo tipo o círculos de Apolonio. Ver Figura 3.2.20.

En el caso de que\(T\) tenga un punto fijo\(p\text{,}\) el mapa de conjugación\(Sz=\frac{1}{z-p}\) envía\(p\to \infty\text{,}\) así\(S^{-1}\)\(S^{-1}\) mapas\(\infty \to p\text{,}\) y mapea líneas en el\(w\) plano que son paralelas a la línea a través\(0\) y\(\beta\) a clines en el\(z\) -plano que contienen \(p\text{.}\)Cada cline de esta familia es tangente a todos los demás cline de esta familia exactamente en un punto\(p\text{.}\) Clines en esta familia se llaman círculos Steiner degenerados. Ver Figura 3.2.21. El Cuadro 3.2.22 resume la representación gráfica de las transformaciones de Möbius.

Cuadro 3.2.22. Resumen de Steiner circle pictures of Möbius transformations

tipo de forma normal	dinámica gráfica
elíptica	fluir a lo largo de círculos Steiner de segundo tipo
hiperbólico	fluyen a lo largo de círculos Steiner de primer tipo
loxodérmico	composición de flujos elípticos e hiperbólicos
parabólico	fluir a lo largo de círculos Steiner degenerados

Ejercicios

Ejercicio 1

Descomposición de las transformaciones de Möbius en cuatro tipos básicos.

1. Explique por qué una transformación de la forma\(z\to az\text{,}\) con una constante compleja distinta de cero, es una composición de una homotez y una rotación.
2. Identificar explícitamente cada homotez, rotación, traslación e inversión en (3.2.6) a (3.2.9) en la derivación a continuación para el caso\(c\neq 0\text{.}\)

   \ begin {align}
   z &\ a cz+d\ label {mobiusdecompfirst}\ tag {3.2.6}\\
   &\ a\ frac {1} {cz+d}\ tag {3.2.7}\\
   &\ a\ frac {bc-ad} {cz+d} + a\ tag {3.2.8}\\
   &\ a
   \ frac {1} {c}\ left (\ frac {bc-ad} {cz+d} + a\ derecha)\ label { mobiusdecomplast}\ tag {3.2.9}\\
   & =\ frac {az+b} {cz+d}\ tag {3.2.10}
   \ end {align}

3. Escribe tu propia descomposición para el caso\(c=0\text{.}\)

Ejercicio 2

Forma explícita para la transformación\(\) (⋅, z1, z2, z3).

1. Demostrar que, para el caso especial cuando\(z_1,z_2,z_3\) son complejos (es decir, ninguno de los tres puntos lo es\(\infty\)), tenemos lo siguiente.

   \ begin {align}
   (\ cdot, z_1, z_2, z_3) &=
   \ left [z\ to\ frac {z-z_2} {z-z_3}\ frac {z_1-z_3} {z_1-z_2}\ derecha]\ label {mob10inftyform}\ tag {3.2.11}\\
   (z_0, z_1, z_2, z_3) &=\ frac {z_0-z_2} {z_0-z_3}\ frac {z_1-z_3} {z_1-z_2}\ label {crossratiofracform}\ tag {3.2.12}
   \ end {align}

2. Encuentra fórmulas explícitas para\((\cdot,z_1,z_2,z_3)\) cuándo y\(z_1=\infty\text{,}\) luego haz lo mismo para\(z_2=\infty\) y\(z_3=\infty\text{.}\)

Ejercicio 3

Encuentra transformaciones de Möbius que realicen las siguientes asignaciones.

1. \(\displaystyle 1\to a, 0\to b, \infty\to c\)
2. \(\displaystyle a\to d, b\to e, c\to f\)

Ejercicio 4

Demostrar Proposición 3.2.12. Sugerencia: Vamos\(Tz=\frac{az+b}{cz+d}\text{,}\) luego manipular\(Tz=(Tz)^\ast\) a una ecuación con\(|z|^2,z,z^\ast\) términos y coeficientes que involucran\(a,b,c,d\) y sus conjugados. Luego use “complejo completando el cuadrado” (ver (1.1.24)). La siguiente pista muestra una versión de una ecuación circular; mira si es necesario, y úsala para trabajar parcialmente hacia adelante desde\(Tz=(Tz)^\ast\text{,}\) y parcialmente hacia atrás desde la ecuación en la pista.

Pista

\ (\ izquierda| z-\ izquierda (\ frac {a^\ ast d-bc^\ ast} {ac^\ ast -a^\ ast
c}\ derecha)\ derecha|^2 =\ izquierda|\ frac {ad-bc} {ac^\ ast -a^\ ast c}\ derecha|^2\)

Ejercicio 5

Demostrar Lema 3.2.18.

Ejercicio 6

Simetría con respecto a una clina.

1. Demostrar Corolario 3.2.17.
2. Dejar\(C\) ser el círculo de la unidad. Mostrar esa\(z^{\ast C} = 1/z^\ast\text{.}\) Sugerencia: Esto es solo un cálculo, pero la elección de\(z_1,z_2,z_3\) podría hacerlo más o menos tedioso. Podrías probar\(\omega,\omega^2,\omega^3=1\text{,}\) donde\(\omega=e^{2\pi i/3}\text{.}\)
3. Ahora vamos a\(C\) ser un círculo con centro a y radio\(r\gt 0\text{.}\) Usa la Proposición 3.2.16 para mostrar que\(z^{\ast C} = \frac{r^2}{(z-a)^\ast}+a\text{.}\)
4. Dejar\(C\) ser una línea recta. Demostrar que\(z^{\ast C}\) es el reflejo de\(z\) través\(C\text{.}\)

Formas normales y círculos Steiner.

Ejercicio 7

Encuentra la forma normal y dibuja una gráfica usando círculos Steiner para las siguientes transformaciones.

1. \(\displaystyle z\to \frac{1}{z}\)
2. \(\displaystyle z\to \frac{3z-1}{z+1}\)

Ejercicio 8

Dejar\(p\) ser el único punto fijo de una transformación de Möbius que se conjuga a\(w\to w+\beta\) vía\(Sz=\frac{1}{z-p}\text{.}\) Mostrar que la línea única en el degenerado Steiner clines a través\(p\) es paralela a la dirección dada por\(\beta^\ast\text{.}\)

Pista

Mostrar que\(S^{-1}w=\frac{pw+1}{w}\text{,}\) así\(S^{-1}\) lleva\(0,\beta,\infty\) a\(\infty,\frac{p\beta+1}{\beta},p\text{.}\) Así la única línea recta de Steiner degenerada\(p\) está en la dirección dada por\ (\ frac {p\ beta+1} {\ beta} -p
=\ frac {1} {\ beta}\ propto\ beta^\ ast\ text {.}\)

Ejercicio 9

Mostrar que un círculo (generalizado) de Apolonio (un círculo Steiner del segundo tipo) se caracteriza como el conjunto de puntos de la forma

\ begin {ecuación*}
C=\ izquierda\ {P\ in\ mathbb {C}\ colon\ frac {d (P, A)} {d (P, B)} =k\ derecha\}
\ final {ecuación*}

para algunos\(A,B\in \mathbb{C}\) y algunos constantes reales\(k\gt 0\text{.}\)