3.3: Geometría hiperbólica

Antes del descubrimiento de la geometría hiperbólica, se creía que la geometría euclidiana era la única geometría posible del plano. De hecho, la geometría hiperbólica surgió como un subproducto de los esfuerzos para demostrar que no había alternativa a la geometría euclidiana. En esta sección, presentamos una versión kleiniana de geometría hiperbólica.

Definición 3.3.1.

Dejar\(\mathbb{D}=\{z\colon |z|\lt 1\}\) denotar el disco de la unidad abierta en el plano complejo. El grupo hiperbólico, denotado\(\mathbf{H}\), es el subgrupo del grupo\(\mathbf{M}\) de transformaciones Möbius que\(\mathbb{D}\) se mapean sobre sí mismo. El par\((\mathbb{D},\mathbf{H})\) es el modelo de disco (Poincaré) de geometría hiperbólica.

Comentarios sobre terminología: Cuidado con los dos significados diferentes del adjetivo “hiperbólico”. Decir que una transformación de Möbius es hiperbólica significa que está conjugada con una homotez (ver Subsección 3.2.4). Eso no es lo mismo que un elemento del grupo de transformaciones hiperbólicas.

El grupo de transformación hiperbólica

Comenzamos con una observación sobre las transformaciones de Möbius que mapean discos abiertos sobre sí mismos. Dejar\(C=\{z\colon |z-a|=r\}\) ser un círculo con centro a y radio\ (r\ gt
0\ text {.}\) Dejar\(D=\{z\colon |z-a|\lt r\}\) denotar el disco abierto delimitado por\(C\text{,}\) y dejar\(E=\{z\colon |z-a|\gt r\}\) denotar el complemento del disco cerrado delimitado por\(C\text{.}\) Ahora supongamos que una transformación de Möbius se\(T\) mapea\(D\) sobre sí mismo. Cada punto\(z\in D\) tiene un punto simétrico\(z^{\ast C}\in E\text{,}\) y debido a que\(T\) lleva puntos simétricos a puntos simétricos (Proposición 3.2.16), debe ser el que se\(T\) mapee\(E\) sobre sí mismo. Por proceso de eliminación, debe ser que se\(T\) mapea\(C\) sobre sí mismo. Así hemos probado como caso especial el siguiente Lema.

Lema 3.3.2.

Si\(T\in \mathbf{H}\text{,}\) entonces\(T\) mapea el círculo de la unidad sobre sí mismo.

Dado\(T\in \mathbf{H}\text{,}\) deja\(z_0\in\mathbb{D}\) ser el punto que\(T\) mapea a\(0\text{.}\) Debe ser que\(T\) mapee el punto simétrico\(\frac{1}{z^\ast}\) a\(\infty\text{,}\) así\(T\) tiene la forma

\ begin {ecuación*}
Tz =\ alfa\ frac {z-z_0} {z-\ frac {1} {z_0^\ ast}} =
\ alpha z_0^\ ast\ frac {z-z_0} {1-z_0^\ ast z}
\ end {ecuación*}

para algunos\(\alpha\text{.}\) Una derivación directa muestra que\(|\alpha z_0^\ast|=1\text{,}\) para que tengamos (3.3.1) a continuación. Otro cálculo establece una fórmula alternativa (3.3.2) para\(T\in \mathbf{H}\text{.}\) Ver Ejercicio 3.3.6.1.

Proposición 3.3.3.

Una transformación de Möbius\(T\) está en\(\mathbf{H}\) H si un solo si se\(T\) puede escribir en la forma

\ begin {ecuación}
tz=e^ {it}\ frac {z-z_0} {1-z_0^\ ast z}\ label {diskhypgptrans0inftyform}\ tag {3.3.1}
\ end {ecuación}

para algunos\(t\in \mathbb{R}\) y\(z_0\in \mathbb{D}\text{.}\) Alternativamente, tenemos\(T\in \mathbf{H}\) si y solo si se\(T\) puede escribir en el formulario

\ begin {ecuación}
Tz=\ frac {az+b} {b^\ ast
z+a^\ ast}\ label {diskhypgptranssu11form}\ tag {3.3.2}
\ end {ecuación}

para algunos de\(a,b\in \mathbb{C}\) tal manera que\(|a|^2-|b|^2=1\text{.}\)

Clasificación de clinos en geometría hiperbólica

Los clinos de geometría de Möbius se clasifican en varios tipos en geometría hiperbólica, como se resume en la Tabla 3.3.4.

Cuadro 3.3.4. Clines en geometría hiperbólica

tipo de curva hiperbólica	tipo cline
línea recta hiperbólica	un cline que intersecta el círculo unitario en ángulo recto
círculo hiperbólico	un círculo completamente contenido en\(\mathbb{D}\)
horociclo	un círculo con todos menos un punto adentro\(\mathbb{D}\), tangente al círculo unitario
hiperciclo	una clina que cruza el círculo unitario en un ángulo no recto

Formas normales para el grupo hiperbólico

En esta subsección, se sigue el desarrollo de formas normales para transformaciones generales de Möbius dadas en la Subsección 3.2.4 para derivar formas normales e interpretaciones gráficas para transformaciones en el grupo hiperbólico. Comenzamos con una observación sobre puntos fijos de una transformación de Möbius que mapea un cline a sí mismo.

Lema 3.3.5.

Deja\(T\in \mathbf{M}\) y deja\(C\) ser un cline. Si\(Tz=z\text{,}\) entonces\(T(z^{\ast C})=z^{\ast C}\text{.}\)

Comprobante.

Aplicar Proposición 3.2.16

Ahora dejemos\(T\) ser un elemento no identitario de\(\mathbf{H}\). El hecho de que\(T\) mapea el círculo unitario a sí mismo implica que hay exactamente tres casos posibles para puntos fijos de\(T\text{.}\)

1. Hay un par de puntos fijos\(p,q\) con\(|p|\lt 1\text{,}\)\(|q|\gt 1\text{,}\) y es\(q=\frac{1}{p^\ast}\text{,}\) decir,\(p,q\) son un par de puntos simétricos (con respecto al círculo unitario) que no se encuentran en el círculo unitario.
2. Hay un par de puntos fijos que se encuentran en el círculo unitario.
3. Hay un solo punto fijo que se encuentra en el círculo unitario.

Punto de control 3.3.6.

Dar un argumento para justificar los tres casos anteriores.

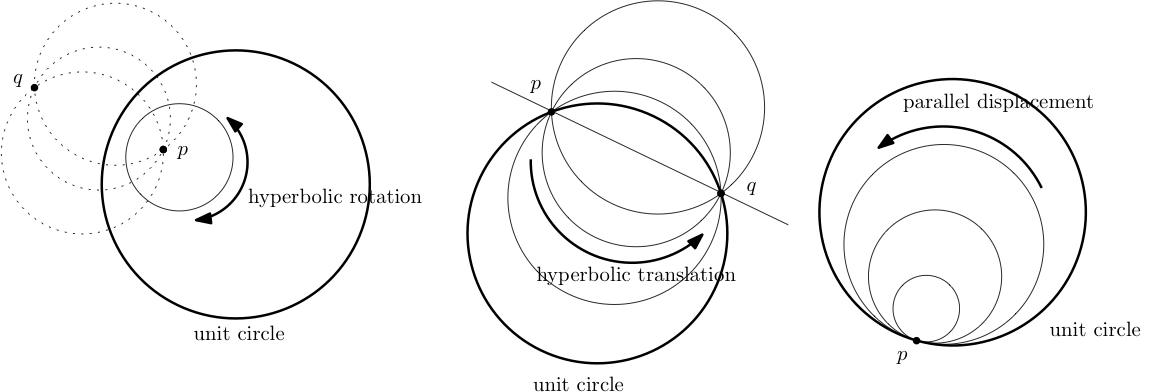
Figura 3.3.7. Tres tipos de transformaciones hiperbólicas

Para los casos\(1\) y\(2\) superiores, el mapa\(T\) que actúa en el\(z\) plano -está conjugado con el mapa\(U=S\circ T\circ S^{-1}\) que actúa en el\(w\) plano por\(Uw=\lambda w\text{,}\) para algunos distintos de cero\(\lambda\in\mathbb{C}\text{,}\) a través del mapa\(w=Sz=\frac{z-p}{z-q}\text{.}\) En caso\(1\) de que el mapa\(S\) lleve el círculo unitario a algún polar círculo,\(C\text{,}\) dígalo\(U\) debe mapearse\(C\) a sí mismo. De ello se deduce que\(|\lambda|=1\text{,}\) así el tipo de forma normal de Möbius para\(T\) es elíptica. La acción de\(T\) es una rotación sobre círculos Steiner de segundo tipo (círculos hiperbólicos) con respecto a los puntos fijos\(p,q\text{.}\) Una transformación\(T\in \mathbf{H}\) de este tipo se denomina rotación hiperbólica. Ver Figura 3.3.7.

Por caso\(2\), el mapa\(w=Sz=\frac{z-p}{z-q}\) lleva el círculo unitario a una línea recta, digamos a\(L\text{,}\) través del origen, por lo que\(U=S\circ T\circ S^{-1}\) debe mapearse\(L\) a sí mismo. De ello se deduce que\(\lambda\) es real. Ya que\(\mathbb{D}\) los\(S\) mapas a uno de los dos medios planos a cada lado\(L\text{,}\) del mapa\(U\) deben tomar este medio plano a sí mismo. Si sigue ese\(\lambda\) debe ser un número real positivo, por lo que el tipo de forma normal de Möbius para\(T\) es hiperbólico. La acción de\(T\) es un flujo sobre círculos Steiner de primer tipo (hiperciclos y una línea recta hiperbólica) con respecto a los puntos fijos\(p,q\text{.}\) Una transformación\(T\in \mathbf{H}\) de este tipo se llama traducción hiperbólica. Ver Figura 3.3.7.

Para el caso\(3\), el mapa de conjugación\(w=Sz=\frac{1}{z-p}\) toma\(T\) a\(U=S\circ T\circ S^{-1}\) de la forma\(Uw=w+\beta\) para algunos\(\beta\neq 0\text{.}\) El tipo de forma normal de Möbius para\(T\) es parabólico. La acción de\(T\) es un flujo a lo largo de círculos Steiner degenerados (horociclos) tangentes al círculo unitario en\(p\text{.}\) Una transformación\(T\in \mathbf{H}\) de este tipo se llama desplazamiento paralelo. Ver Figura 3.3.7.

Esto completa la lista de tipos de transformación para el grupo hiperbólico. Véase el Cuadro 3.3.8 para un resumen.

Cuadro 3.3.8. Formas normales para el grupo hiperbólico

tipo de transformación hiperbólica	Möbius forma normal	dinámica gráfica
rotación hiperbólica	elíptica	flujo alrededor de círculos hiperbólicos
Desplazamiento paralelo	parabólico	flujo alrededor de horociclos
traducción hiperbólica	hiperbólico	flujo a lo largo de hiperciclos
(ninguno)	loxodérmico

Longitud y área hiperbólica

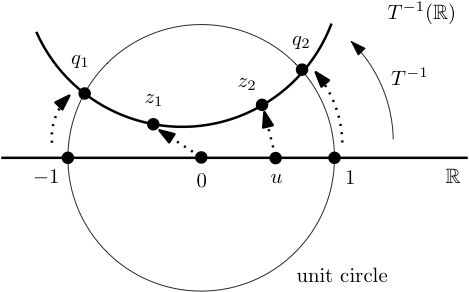
Figura 3.3.9. Construyendo la línea recta hiperbólica que contiene dos puntos\(z_1,z_2\)

Dejar\(z_1,z_2\) ser distintos puntos en\(\mathbb{D}\) Let\(T\in\mathbf{H}\) be la transformación que envía\(z_1\to 0\) y\(z_2\to  u\gt 0\text{.}\) Entonces\(T^{-1}(\mathbb{R})\) es una línea recta hiperbólica que contiene\(z_1,z_2\text{.}\) Let\(q_1=T^{-1}(-1)\) and\(q_2=T^{-1}(1)\text{.}\) See Figura 3.3.9.

Punto de control 3.3.10.

Utilice la Proposición 3.3.3 para escribir una fórmula para la transformación\(T\) en el párrafo anterior.

Solución

\(Sz=\frac{z-z_1}{1-z_1^\ast z}\text{,}\)Vamos a dejar\ (t=-\ arg
(Sz_2)\ text {,}\) y vamos\(Tz=e^{it}Sz\text{,}\) así que tenemos\(Tz_1=0\) y\(Tz_2=u\gt 0\text{.}\) Porque\(T\in \mathbf{H}\text{,}\)\(T\) está determinado por los dos parámetros.

Un simple cálculo verifica que\((0,u,1,-1)=\frac{1+u}{1-u}\text{.}\) Por invarianza de la relación cruzada, tenemos\((z_1,z_2,q_2,q_1)=\frac{1+u}{1-u}\text{.}\) For\ (0\ leq u\ lt
1\ text {,}\) tenemos

\ begin {ecuación*}
1\ leq\ frac {1+u} {1-u}\ lt\ infty
\ end {ecuación*}

con igualdad a la izquierda si y sólo si\(u=0\text{.}\)

Punto de control 3.3.11.

Haz el cálculo simple mencionado anteriormente.

Pista

Uso (3.2.12).

Ahora, dado cualquier punto\(z_1,z_2\) en\(\mathbb{D}\) no necesariamente distinto, definir la cantidad\(d(z_1,z_2)\) por

\ begin {ecuación}
d (z_1, z_2) =
\ left\ {\ begin {array} {cc}\ ln ((z_1, z_2, q_2, q_1)) & z_1\ neq
z_2\\ 0 & z_1=z_2\ end {array}\ right. \ label {hyperbolicdistdef}\ tag {3.3.3}
\ end {ecuación}

donde\(q_1,q_2\) están los puntos ideales en la línea recta hiperbólica conectando\(z_1,z_2\) (con cada uno\(q_i\) al\(z_i\) final de la línea) como se describió anteriormente, en el caso\(z_1\neq z_2\text{.}\) De la discusión anterior tenemos

\ begin {ecuación}
d (z_1, z_2) =\ ln\ izquierda (\ frac {1+u} {1-u}\ derecha)\ label {disthyperbolicfrac}\ tag {3.3.4}
\ end {ecuación}

donde\(u=\left|\frac{z_2-z_1}{1-z_1^\ast z_2}\right|\text{.}\)

Punto de control 3.3.12.

Justificar el valor de\(u\) in (3.3.4).

Proposición 3.3.13.

La función\(d\) dada por (3.3.3) es invariante bajo la acción del grupo hiperbólico. Es decir, tenemos

\ begin {ecuación}
d (z_1, z_2) = d (Tz_1, Tz_2)\ tag {3.3.5}
\ end {ecuación}

para todos\(z_1,z_2\in \mathbb{D}\) y para todos\(T\in\mathbf{H}\text{.}\)

Punto de control 3.3.14.

Demostrar Proposición 3.3.13.

La siguiente Proposición muestra que\(d\) es una métrica sobre el espacio hiperbólico, y justifica referirse\(d(z_1,z_2)\) como la distancia (hiperbólica) entre los puntos\(z_1,z_2.\)

Proposición 3.3.15.

La función\(d\) dada por (3.3.3) define una métrica en Es\(\mathbb{D}\text{.}\) decir,\(d\) satisface

1. \(d(z_1,z_2)\geq 0\text{,}\)y\(d(z_1,z_2)=0\) si y solo si\(z_1=z_2\)
2. \(\displaystyle d(z_1,z_2)=d(z_2,z_1)\)
3. \(d(z_1,z_3)\leq d(z_1,z_2)+d(z_2,z_3)\)(la desigualdad del triángulo)

para todos\(z_1,z_2,z_3\) en\(\mathbb{D}\text{.}\)

Comprobante.

La propiedad 1 sigue inmediatamente de (3.3.4). La propiedad 2 es un cálculo simple: simplemente escriba las expresiones de relación cruzada para\(d(z_1,z_2)\)\(d(z_2,z_1)\) y compare. El comprobante de Inmueble 3 se esboza en el ejercicio Ejercicio 3.3.6.4.

Ahora vamos a\(\gamma\) ser una curva parametrizada por\ (t\ a z (t) =x (t)
+ iy (t)\ text {,}\) donde\(x(t),y(t)\) están diferenciables funciones de valor real del parámetro real\(t\) en un intervalo\(a\lt t\lt b\text{.}\) Considera un segmento corto de\(\gamma\text{,}\) digamos, en un intervalo\ (t_0\ leq t\ leq
t_1\ text {.}\) Let\(z_0=z(t_0)\) y\(z_1=z(t_1)\text{.}\) Entonces tenemos\(d(z(t_0),z(t_1))=\ln\left(\frac{1+u}{1-u}\right)\) donde\(u=\left|\frac{z_1-z_0}{1-z_0^\ast(z_1)}\right|\text{.}\) La cantidad\(|z_1-z_0|\) es bien aproximada por\(|z'(t_0)|dt\text{,}\) donde\(z'(t)=x'(t)+iy'(t)\) y\(dt=t_1-t_0\text{.}\) Así,\(u\) es bien aproximada por\(\frac{|z'(t_0)|}{1-|z(t_0)|^2}\;dt\text{.}\) La aproximación de Taylor de primer orden para\(\ln((1+u)/(1-u))\) es \(2u\text{.}\)Armando todo esto, tenemos lo siguiente.

\ begin {ecuación}
\ texto {Longitud} (\ gamma) =2\ int_a^b\ frac {|z' (t) |} {1-|z (t) |^2}\; dt\ label {hyperboliclength formula}\ tag {3.3.6}
\ end {ecuación}

Punto de control 3.3.16.

Demostrar que la aproximación de Taylor de primer orden\(\ln((1+u)/(1-u))\) es\(2u\text{.}\)

Punto de control 3.3.17.

Encuentra la longitud del círculo hiperbólico parametrizado\(z(t) = \alpha e^{it}\) por\(0\leq t\leq 2\pi\text{,}\) donde\(0\lt \alpha\lt 1\)

Concluimos esta subsección sobre longitud y área hiperbólica con una fórmula integral para el área de una región\(R\) en el\(\mathbb{D}\text{,}\) seguimiento del desarrollo en [4]. En función de las dos variables reales\(r\) y\(\theta\text{,}\) la expresión de forma polar\(z=re^{i\theta}\) da lugar a las dos curvas parametrizadas\(r\to z_1(r)=re^{i\theta}\) (donde\(\theta\) es constante) y\(\theta \to z_2(\theta) = re^{i\theta}\) (donde\(r\) es constante). Usando\ (z_1' (r) =
e^ {i\ theta}\) y\(z_2'(\theta)=ire^{i\theta}\text{,}\) el diferencial de longitud de arco\(ds=\frac{2|z'(t)|\;dt}{1-|z(t)|^2}\) para las dos curvas son los siguientes.

\ begin {ecuación*}
\ frac {2|e^ {i\ theta} |\; dr} {1-r^2} =\ frac {2\; dr} {1-r^2}
\ ;(\ texto {para curva} z_1)
\ end {ecuación*}

\ begin {ecuación*}
\ frac {2|ire^ {i\ theta} |\; dr} {1-r^2} =\ frac {2r\; dr} {1-r^2}
\ ;(\ texto {para curva} z_2)
\ end {ecuación*}

\(dA=\frac{4r\;dr\;d\theta}{(1-r^2)^2}\text{,}\)Así tenemos para que el área de una región\(R\) sea

\ begin {ecuación}
\ texto {Área} (R) =\ iint_r
dA =\ iint_r\ frac {4r\; dr\; d\ theta} {(1-r^2) ^2}. \ label {hyperbolicareaintformula}\ tag {3.3.10}
\ end {ecuación}

Punto de control 3.3.18.

Encuentra el área del disco hiperbólico\ (\ {|z|\ leq
\ alpha\}\ text {,}\) para\(0\lt \alpha\lt 1\text{.}\)

El modelo de medio plano superior

Definición 3.3.19. El modelo de medio plano superior de geometría hiperbólica.

Vamos a\(\mathbb{U}=\{z\colon Im(z)\gt 0\}=\{z\colon Im(z)\gt 0\}\) denotar la mitad superior del plano complejo por encima del eje real, y dejar\(\mathbf{H}_{\mathbb{U}}\) denotar el subgrupo del grupo\(\mathbf{M}\) de transformaciones Möbius que mapean\(\mathbb{U}\) sobre sí mismo. El par\((\mathbb{U},\mathbf{H}_{\mathbb{U}})\) es el modelo de medio plano superior de geometría hiperbólica.

Proposición 3.3.20.

Una transformación de Möbius\(T\) está en\(\mathbf{H}_{\mathbb{U}}\) si y solo si se\(T\) puede escribir en la forma

\ begin {ecuación}
Tz=\ frac {az+b} {cz+d}\ label {halfplanhypgptrans}\ tag {3.3.11}
\ end {ecuación}

tales que\(a,b,c,d\) son reales y\ (ad-bc\ gt
0\ text {.}\)

Las líneas rectas hiperbólicas en el modelo de medio plano superior son clines que intersectan la línea real en ángulo recto. La distancia hiperbólica entre dos puntos\(z_1,z_2\) en el medio plano superior es

\ begin {ecuación}
d (z_1, z_2) =\ ln ((z_1, z_2, q_2, q_1))\ tag {3.3.12}
\ end {ecuación}

donde\(q_1,q_2\) están los puntos en la línea real (extendida) al final de la recta hiperbólica que contiene\(z_1,z_2\text{,}\) con cada uno\(q_i\) en el mismo “lado” que el correspondiente\(z_i\text{.}\) La longitud hiperbólica de una curva\(\gamma\) parametrizada por\ (t\ a
z (t) =x (t) +iy (t)\) on el intervalo\(a\leq t\leq b\) es

\ begin {ecuación}
\ texto {Longitud} (\ gamma) =\ int_a^b
\ frac {|z' (t) |} {y (t)}\; dt. \ label {halfplanelengthformula}\ tag {3.3.13}
\ end {ecuación}

El área hiperbólica de una región\(R\) en\(\mathbb{U}\)

\ begin {ecuación}
\ texto {Área} (R) =\ iint_r
dA =\ iint_r\ frac {dx\; dy} {y^2}. \ label {upperhalfplaneareaintformula}\ tag {3.3.14}
\ end {ecuación}

Ejercicios

Ejercicio 1

Demostrar la Proposición 3.3.3 utilizando el siguiente esquema.

1. Complete el comprobante de (3.3.1) usando este esquema: Dejar\(|z|=1\) y aplicar Lemma 3.3.2. Tenemos

   \ begin {ecuación*}
   1=|Tz|=|\ alpha z_0^\ ast|\ izquierda|\ frac {z-z_0} {1-z_0^\ ast
   z}\ derecha|.
   \ end {ecuación*}

   Continuar con esta derivación para demostrar que\(|\alpha z_0^\ast|=1\text{.}\)
2. Demostrar (3.3.2) verificando lo siguiente. Dado\(z_0\in \mathbb{D}\) y\(t\in \mathbb{R}\text{,}\) mostrar que las asignaciones\ (a=\ frac {e^ {it/2}} {\ sqrt {1-|z_0|^2}},
   b=\ frac {-e^ {it/2} z_0} {\ sqrt {1-|z_0|^2}}\) satisfacen\(|a|^2-|b|^2=1\) y que

   \ begin {ecuación}
   \ frac {az+b} {b^\ ast z+a^\ ast} = e^ {it}\ frac {z-z_0} {1-z_0^\ ast z}\ text {.} \ label {twohyptransformssame}\ tag {3.3.15}
   \ fin {ecuación}

   Por el contrario, dado\(a,b\in \mathbb{C}\) con\(|a|^2-|b|^2=1\text{,}\) mostrar que las asignaciones\(t=2\arg a, z_0=-\frac{b}{a}\) satisfacen\ (z_0
   \ in\ mathbb {D}\ text {,}\) y que (3.3.15) sostiene.

Ejercicio 2

Dos puntos determinan una línea.

Dejar\(p,q\) ser distintos puntos en\(\mathbb{D}\text{.}\) Mostrar que hay una línea recta hiperbólica única que contiene\(p\) y\(q\text{.}\)

Pista

Empieza por elegir una transformación que mande\(p\to 0\text{.}\)

Ejercicio 3

Dejar caer una perpendicular de un punto a una línea.

Dejar\(L\) ser una línea recta hiperbólica y dejar\(p\in\mathbb{D}\) ser un punto no en\(L\text{.}\) Mostrar que hay una línea recta hiperbólica única\(M\) que contiene\(p\) y es ortogonal a\(L\text{.}\)

Pista

Empieza por elegir una transformación que mande\(p\to 0\text{.}\)

Ejercicio 4

La desigualdad triangular para la métrica hiperbólica.

\(d(a,b)\leq d(a,c)+d(c,b)\)Demuéstralo para todos\(a,b,c\) en el\(\mathbb{D}\) uso del esquema a continuación.

1. Mostrar que la desigualdad del triángulo se mantiene con estricta igualdad cuando\(a,b,c\) son colineales y\(c\) está entre\(a\) y\(b\text{.}\) Sugerencia: Este es un cálculo sencillo utilizando las expresiones de relación cruzada para los valores de\(d\text{.}\)
2. Mostrar que la desigualdad triangular se mantiene con estricta desigualdad cuando\(a,b,c\) son colineales y no\(c\) está entre\(a\) y\(b\text{.}\)
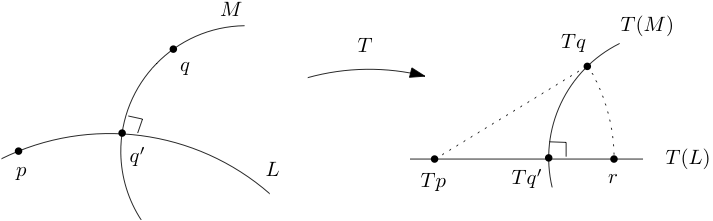
3. Dejar\(p\in \mathbb{D}\) mentir sobre una línea hiperbólica\(L\text{,}\)\(q\in \mathbb{D}\text{,}\) dejar\(M\) ser una línea a través de\(q\) perpendicular a\(L\) (esta línea\(M\) existe por el Ejercicio 3.3.6.3), y dejar\(q'\) ser el punto de intersección de\(L,M\text{.}\) Mostrar esa\(d(p,q')\leq d(p,q)\text{.}\) Sugerencia: aplicar\ (T\ in
   \ mathbf {H}\) que toma\(p\to 0\) y toma\(L\to \mathbb{R}\text{.}\) Let\(t=-\arg(Tq)\) if\(Re(Tq)\geq 0\) y\(t=\pi-\arg(Tq)\) let\(t=\pi-\arg(Tq)\) si Let\(r=e^{it}Tq\text{.}\) Ver Figura 3.3.21.
4. Dado arbitrario\(a,b,c\text{,}\) aplicar una transformación\(T\) para enviar\(a\to 0\) y\(b\) a un punto real no negativo. Deja caer una perpendicular de Tc a la línea real, digamos, para\(c'\text{.}\) Aplicar resultados de los pasos anteriores de este esquema.

Figura 3.3.21.

Ejercicio 5

Demostrar Proposición 3.3.20.

Ejercicio 6

Longitud integral en el modelo de medio plano superior.

Este ejercicio es para establecer (3.3.13). La estrategia es obtener la expresión diferencial

\ begin {ecuación*}
d (z (t_0), z (t_1))\ approx\ frac {|z' (t) |dt} {y (t)}
\ final {ecuación*}

para una curva\(z(t)=x(t)+iy(t)\) con\(z(t_0)=z_0\text{,}\)\(z(t_1)=z_1\text{,}\) y\(dt=t_1=t_0\) usando la siguiente secuencia de pasos.

• Primero, mapear\(z_0,z_1\) adentro\(\mathbb{U}\) a\(z_0',z_1'\) in\(\mathbb{D}\) usando una transformación\(\mu\) que preserva la distancia.
• Usando el análisis que usamos para obtener la fórmula integral de longitud del modelo de disco (3.3.6), tenemos

  \ begin {ecuación*}
  d (z_0', z_1') =\ ln\ izquierda (\ frac {1+u} {1-u}\ derecha)
  \ end {ecuación*}

  donde\ (u=\ izquierda|\ frac {z_1'-z_0'} {1- (z_0') ^\ ast
  z_1'}\ derecha|\ text {.}\)
• Traducir la expresión anterior en términos de\(z_0,z_1\text{,}\) y mostrar que la aproximación diferencial es\(\frac{|z'(t)|dt}{y(t)}\text{.}\)

Complete las partes del ejercicio a continuación para llevar a cabo la estrategia que se acaba de describir.

1. Espectáculo que\(\mu z=\frac{z-i}{z+i}\) lleva\(\mathbb{U}\) a\(\mathbb{D}\).
2. Deja\(z_0'=\mu z_0\) y\(z_1'=\mu z_1\text{.}\) muestra eso

   \ begin {ecuación*}
   \ frac {z_1'-z_0'} {1- (z_0') ^\ ast
   z_1'} =e^ {it}\ frac {z_1-z_0} {z_0^\ ast - z_1}
   \ end {ecuación*}

   para algunos reales\(t\text{.}\)
3. Dejar\ (u=\ izquierda|\ frac {z_1-z_0} {z_0^\ ast -
   z_1}\ derecha|\ text {.}\) Mostrar eso

   \ begin {ecuación*}
   \ ln\ izquierda (\ frac {1+u} {1-u}\ derecha)\ approx\ frac {|z (t) |dt} {y (t)}.
   \ end {ecuación*}

Ejercicio 7

Área integral en el modelo de medio plano superior.

Adaptar el argumento en el párrafo anterior a la integral de área del modelo de disco (3.3.10) para establecer la integral de área de medio plano superior (3.3.14).

Figura 3.3.22. Triángulo hiperbólico\(\triangle ABC\)

Área de un triángulo hiperbólico.

La siguiente secuencia de ejercicios establece la fórmula de área para triángulos hiperbólicos.

Ejercicio 8

Área de un triángulo dobles-asintótico.

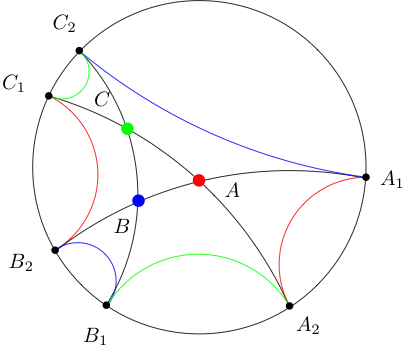
Un triángulo con un vértice adentro\(\mathbb{D}\) y dos vértices en el círculo unitario, conectados por arcos de círculos que son ortogonales al círculo unitario, se llama triángulo hiperbólico doblemente-asintótico. Ejemplos son\(\triangle AA_1A_2\text{,}\)\ (\ triángulo
BB_1B_2\ text {,}\) y\(\triangle CC_1C_2\) en la Figura 3.3.22.

1. Explique por qué cualquier triángulo dobles-asintótico en el medio plano superior es congruente con el que se muestra en la Figura 3.3.23 para algún ángulo\(\alpha\text{.}\)
2. Ahora use la fórmula de integración para el modelo de medio plano superior para mostrar que el área del triángulo dobles-asintótico con ángulo\(\alpha\) (en el vértice interior a\(\mathbb{U}\)) es\(\pi-\alpha\text{.}\)

Figura 3.3.23. Triángulo hiperbólico doble asintótico en el medio plano superior con vértices\(1,p,\infty\) con\(p\) en la mitad superior del círculo unitario

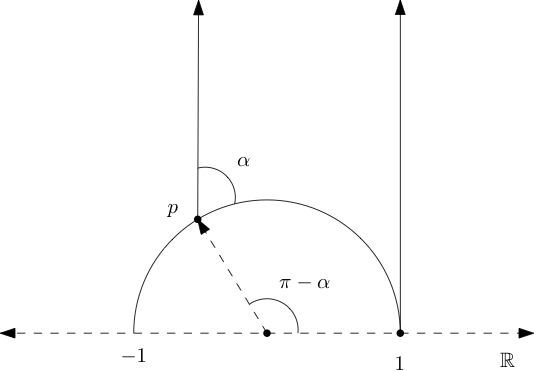
Ejercicio 9

Área de un n-gon asintótico.

Un polígono con\(n\geq 3\) vértices en el círculo unitario, conectado por arcos de círculos que son ortogonales al círculo unitario, se denomina\(n\) -gon asintótico. Un ejemplo de hexágono asintótico es la figura con vértices\(A_1,A_2,B_1,B_2,C_2,C_2\) conectados por las líneas hiperbólicas coloreadas en la Figura 3.3.22. Mostrar que el área de un\(n\) -gon asintótico es\(\pi(n-2)\text{.}\)

Pista

Particionar el\(n\) -gon asintótico\(n\) en triángulos dobles-asintóticos.

Ejercicio 10

Área de un triángulo hiperbólico.

Dejar\(\triangle ABC\) ser un triángulo hiperbólico. Extienda los tres lados\(AB\text{,}\)\(BC\text{,}\)\(AC\) a seis puntos en el círculo unitario. Ver Figura 3.3.22. Utilice una partición del hexágono asintótico cuyos vértices son estos seis puntos para mostrar que el área de\(\triangle ABC\) es

\ begin {ecuación}
\ texto {Área} (\ triángulo
ABC) =\ pi- (\ ángulo A +\ ángulo B +\ ángulo C). \ label {hyperbolictrianglearea}\ tag {3.3.16}
\ end {ecuación}

Pista

Dividir el hexágono asintótico con vértices\(A_1,A_2,B_1,B_2,C_1,C_2\text{.}\) Comienza con los seis triángulos dobles-asintóticos superpuestos cuyas bases son arcos coloreados y cuyo vértice en\(\mathbb{D}\) es el que\(A,B,C\) coincida con el color de la base. Por ejemplo, los dos triángulos rojos dobles-asintóticos son\(\triangle AA_1A_2\) y\ (\ triángulo
AC_1B_2\ text {.}\)