3.5: Geometría Proyectiva

La motivación temprana para el desarrollo de la geometría proyectiva vino de artistas que intentaban resolver problemas prácticos en el dibujo y la pintura en perspectiva. En esta sección, presentamos una versión kleiniana moderna de geometría proyectiva.

A lo largo de esta sección,\(\mathbb{F}\) es un campo,\(V\) es un espacio vectorial sobre\(\mathbb{F}\text{,}\)\(\mathbb{P}(V)=(V\setminus \!\{0\})/\mathbb{F}^\ast\) es el espacio proyectivo, y\(PGL(V)=GL(V)/\mathbb{F}^\ast\) es el grupo de transformación proyectiva. Consulte el Ejercicio 2.5.3.6 para conocer las definiciones y los detalles. Escribiremos\([T]\) para la transformación proyectiva que es la clase de equivalencia de la transformación lineal\(T\) de\(V\text{.}\)

Puntos, líneas y planos proyectivos

Los puntos en el espacio proyectivo corresponden bijectivamente a los subespacios\(1\) -dimensionales de\(V\) vía

\ begin {ecuación*}
[v]\ izquierdafila\ {\ alfa v\ colon\ alfa\ alfa\ in\ mathbb {F}\}.
\ end {ecuación*}

El conjunto de subespacios\(1\) -dimensionales en\(V\text{,}\) denotado\(G(1,V)\text{,}\) es un espacio modelo alternativo para la geometría proyectiva. Por lo general, denotaremos puntos en el espacio proyectivo usando letras mayúsculas, como\(P\text{,}\)\(Q\text{,}\) etc.

Una línea en el espacio proyectivo es un conjunto de la forma

\ comenzar {ecuación*}
\ ell_\ Pi=\ {[v]\ dos puntos v\ in\ Pi\ setmenos\ {0\}\}
\ final {ecuación*}

para algún subespacio\(2\) -dimensional\(\Pi\) en\(V\text{.}\) Así, las líneas proyectivas corresponden bijectivamente a los subespacios\(2\) -dimensionales de\(V\) vía

\ begin {ecuación*}
\ ell_ {\ Pi}\ izquierdafila\ Pi.
\ end {ecuación*}

El conjunto de subespacios\(2\) -dimensionales en\(V\) se denota Los\(G(2,V)\text{.}\) puntos en el espacio proyectivo se denominan colineales si se encuentran juntos en una línea proyectiva. Por lo general, denotaremos líneas proyectivas usando letras minúsculas, como\(\ell\text{,}\)\(m\text{,}\) etc.

Hay un desplazamiento por\(1\) en el uso de la palabra “dimensión” en lo que respecta a los subconjuntos de\(\mathbb{P}(V)\) y el subespacio correspondiente en\(V\text{.}\) En general, un plano\(k\) -dimensional en\(\mathbb{P}(V)\) es un conjunto de la forma\(\{[v]\colon v\in G(k+1,V)\}\text{,}\) donde\(G(d,V)\) denota el conjunto de subespacios\(d\) -dimensionales de\(V\text{.}\) ¹ Planos también se denominan subespacios en el espacio proyectivo, aunque el espacio proyectivo no sea un espacio vectorial.

\(P_1=[v_1],P_2=[v_2],\ldots,P_k=[v_k]\)Se dice que los puntos están en posición general si los vectores\(v_1,v_2,\ldots,v_k\) son independientes en\(V\text{.}\)

Coordenadas

Para lo que resta de esta sección, consideramos\(V=\mathbb{F}^{n+1}\text{.}\) Para legibilidad, escribiremos\(P=[v]=[x_0,x_1,x_2,\ldots,x_{n}]\) (en lugar de lo más engorroso\([(x_0,x_1,x_2,\ldots,x_n)]\) para denotar el punto en el espacio proyectivo que es la clase de equivalencia proyectiva del punto\(v=(x_0,x_1,x_2,\ldots,x_{n})\) en\(\mathbb{F}^{n+1}\text{.}\) Las entradas xi se llaman coordenadas homogéneas de\(P\text{.}\) Si\(x_0\neq 0\text{,}\) entonces

\ begin {ecuación*}
P= [x_0, x_1, x_2,\ ldots, x_n] =\ left [1,\ frac {x_1} {x_0},\ frac {x_2} {x_0},\ ldots,\ frac {x_n} {x_0}\ derecha].
\ end {ecuación*}

Los números\(x_i/x_0\) para\(1\leq i\leq n\) se denominan coordenadas no homogéneas para\(P\text{.}\) Los\(n\) grados de libertad que son aparentes en coordenadas no homogéneas explican por qué\(\mathbb{P}(\mathbb{F}^{n+1})\) se llama\(n\) -dimensional. Muchos textos escriben\(\mathbb{F}\mathbb{P}(n)\text{,}\)\(\mathbb{F}\mathbb{P}_n\text{,}\) o simplemente\(\mathbb{P}_n\) cuando\(\mathbb{F}\) se entiende, para denotar\(\mathbb{P}(\mathbb{F}^{n+1})\text{.}\)

Libertad en las transformaciones proyectivas

En un espacio vectorial\(n\) -dimensional, cualquier vector\(n\) independiente puede mapearse a cualquier otro conjunto de vectores\(n\) independientes mediante una transformación lineal. Por lo tanto, parece un poco sorprendente que en el espacio proyectivo en\(n\) dimensiones\(\mathbb{F}\mathbb{P}_n=\mathbb{P}(\mathbb{F}^{n+1})\text{,}\) sea posible mapear cualquier conjunto de\(n+2\) puntos a cualquier otro conjunto de\(n+2\) puntos, siempre que ambos conjuntos de puntos cumplan con suficientes condiciones de “independencia”. Esta subsección da los detalles de este resultado, denominado Teorema Fundamental de la Geometría Proyectiva.

Dejar\(e_1,e_2,\ldots, e_n,e_{n+1}\) denotar los vectores base estándar para\(\mathbb{F}^{n+1}\) y\(e_0=\sum_{i=1}^{n+1}e_i\text{.}\) let Let\(v_1,v_2,\ldots,v_{n+1}\) ser otra base para\(\mathbb{F}^{n+1}\) y dejar\(c_1,c_2,\ldots,c_{n+1}\) ser escalares distintos de cero. Dejar\(T\) ser la transformación lineal\(T\) de\(\mathbb{F}^{n+1}\) dada por\(e_i\to c_iv_i\) para\(1\leq i\leq n+1\text{.}\) Proyectivamente,\([T]\) envía\([e_i]\to [v_i]\) y\([e_0]\to [\sum_i c_iv_i]\text{.}\)

Ahora supongamos que hay otro mapa con el\([S]\) que concuerda\([T]\) en los\(n+2\) puntos\([e_0],[e_1],[e_2],\ldots,[e_{n+1}]\text{.}\) Entonces\ ([U] := [S] ^ {-1}\ circ
[T]\) arregla todos los puntos\([e_0],[e_1],[e_2],\ldots,[e_{n+1}]\text{.}\) Esto significa que\(Ue_i=k_ie_i\) para algunos escalares distintos de cero\(k_1,k_2,\ldots,k_{n+1}\) y que\(Ue_0=k'e_0\) para algunos\(k'\neq 0\text{.}\) Esto implica

\ begin {ecuación*}
(k_1, k_2,\ ldots, k_ {n+1}) =( k', k',\ ldots, k')
\ end {ecuación*}

así que tenemos\(k'=k_1=k+2=\cdots k_{n+1}\text{.}\) Por lo tanto\([U]\) es la transformación de la identidad, así que\([S]=[T]\text{.}\) acabamos de demostrar el siguiente lema de existencia y singularidad.

Lema 3.5.1.

Dejar\(v_1,v_2,\ldots,v_{n+1}\) ser un conjunto independiente de vectores\(\mathbb{F}^{n+1}\) y dejar que\(v_0=\sum_{i=1}^{n+1}c_iv_i\) para algunos escalares distintos de cero\(c_1,c_2,\ldots,c_{n+1}\text{.}\) Existe una transformación proyectiva única que mapea\([e_i]\to [v_i]\) para\(0\leq i\leq n+1\text{.}\)

Teorema 3.5.2. Teorema Fundamental de la Geometría Proyectiva.

Let\(P_0,P_1,P_2,\ldots,P_{n+1}\) Ser un conjunto de\(n+2\) puntos en\(\mathbb{P}(\mathbb{F}^{n+1})\) tal que todos los subconjuntos de tamaño\(n+1\) están en posición general. \(Q_0,Q_1,Q_2,\ldots,Q_{n+1}\)Sea otro de esos conjuntos. Existe una transformación proyectiva única que mapea\(P_i\to Q_i\text{,}\)

El plano proyectivo real

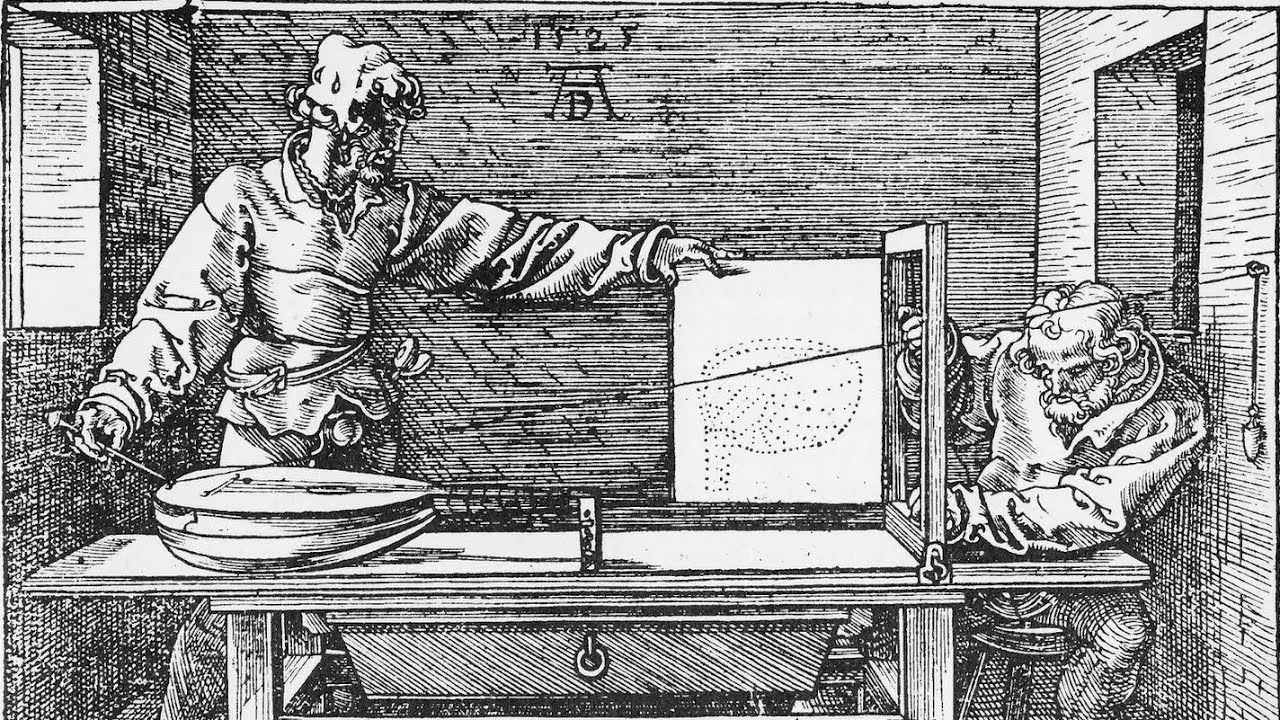
El resto de esta sección se dedica a la geometría plana\(\mathbb{P}(\mathbb{R}^3)=\mathbb{R}\mathbb{P}_2\) llamada plano proyectivo real. Es de interés histórico por su uso práctico temprano por parte de los artistas. Líneas a través del origen en las líneas de visión del\(\mathbb{R}^3\) modelo en el mundo real como se ve desde un ojo colocado en el origen. Un plano que no pasa por el origen modela el “plano de imagen” del lienzo del artista. La Figura 3.5.3 muestra una xilografía de Albrecht Durero que ilustra un gadget de “máquina de perspectiva” utilizado por artistas del siglo XVI para poner en práctica el modelo proyectivo para la creación de imágenes.

Figura 3.5.3. Hombre dibujando un laúd, Alberto Durero, 1525.

Un subespacio bidimensional\(\Pi\) en\(\mathbb{P}^3\) se especifica por un vector normal\(n=(n_1,n_2,n_3)\) a través de la ecuación es\(n\cdot v=0\text{,}\) decir, un punto\(v=(x,y,z)\) se encuentra\(\Pi\) con el vector normal\(n\) si y solo si\(n\cdot v=n_1x+n_2y+n_3z=0\text{.}\) Cualquier múltiplo distinto de cero de también\(n\) es un vector normal para\(\Pi\text{,}\) así el conjunto\(G(2,\mathbb{R})\) de subespacios\(2\) -dimensionales en\(\mathbb{R}^3\) está en correspondencia uno a uno\(\mathbb{R}^3/\mathbb{R}^\ast\text{.}\) Escribiremos\(\ell=[n]=[n_1,n_2,n_3]\) para denotar la línea proyectiva\(\ell\) cuyo subespacio\(2\) -dimensional correspondiente\(\mathbb{R}^3\) tiene vectores normales proporcionales a\((n_1,n_2,n_3)\text{.}\) Cuidado la notación sobrecargada! Debe especificarse si la clase\([v]\) de equivalencia de un vector\(v\) in\(\mathbb{R}^3\) denota un punto proyectivo o una línea proyectiva.

La ecuación tiene\(n\cdot v=0\) sentido proyectivamente. Esto significa que si\(n\cdot v=0\) para vectores\(n,v\text{,}\) entonces

\ begin {ecuación}
(\ alpha
n)\ cdot (\ beta v) =0\;\;\ texto {para todos}\;\;\ alfa,\ beta\ in
\ mathbb {F} ^\ ast\ text {,}\ label {projdotprodzero}\ tag {3.5.1}
\ end {ecuación}

¡aunque el valor del producto dot no esté bien definido para las clases de equivalencia proyectiva! Así escribiremos\(\ell\cdot P=[n_1,n_2,n_3]\cdot [x,y,z]=0\) para una línea proyectiva\(\ell=[n_1,n_2,n_3]\) y un punto proyectivo\(P=[x,y,z]\text{,}\) a media (3.5.1), y haremos la siguiente interpretación del producto punto como relación de incidencia en\(\mathbb{R}\mathbb{P}_2\text{.}\)

\ begin {ecuación}
\ ell\ cdot P = 0\;\;\ Izquierda fila\;
\; P\;\;\ texto {se encuentra en}\;\;\;\ ell\;\;\ Izquierda\;\ Trightarrow
\;\;\ ell\;\ texto {contiene}\;\;\; P.\ etiqueta {3.5.2}
\ final {ecuación}

Dados dos vectores independientes\(v,w\) en\(\mathbb{R}^3\text{,}\) su producto cruzado\(v\times w\) es un vector normal para el espacio\(2\) -dimensional abarcado por\(v,w\text{.}\) Dados subespacios\(2\)\(\Pi,\Sigma\) bidimensionales\(\mathbb{R}^3\) con vectores normales,\(n,m\text{,}\) el producto cruzado\(n\times m\) es un vector que se encuentra a lo largo del subespacio\(1\) -dimensional\(\Pi\cap\Sigma\text{.}\) La bilinaridad del producto cruzado implica que el producto cruzado está bien definido en las clases proyectivas, es decir, podemos escribir\([u]\times [v]:=[u\times v]\text{.}\) Así tenemos lo siguiente.

Proposición 3.5.4.

Dados dos puntos\(P=[u],P'=[u']\) adentro\(\mathbb{R}\mathbb{P}_2\text{,}\) hay una línea proyectiva única\(\overline{PP'}=[u\times u']\) que los contiene. Dadas dos líneas\(\ell=[n],\ell'=[n']\) en\(\mathbb{R}\mathbb{P}_2\text{,}\) hay un punto proyectivo único\([n\times n']\) en su intersección\(\ell\cap \ell'\text{.}\)

Ejercicios

Ejercicio 1

Utilice Lema 3.5.1 para probar el Teorema Fundamental de la Geometría Proyectiva.

Ejercicio 2: Gráficas de coordenadas y coordenadas no homogéneas

Para facilitar el pensamiento sobre la interacción entre la geometría proyectiva\(\mathbb{P}(\mathbb{F}^{n+1})=\mathbb{F}\mathbb{P}_n\) y la geometría de\(\mathbb{F}^{n}\) (en lugar de\(\mathbb{F}^{n+1}\text{!}\)) es útil tener una definición cuidadosa para “tomar coordenadas no homogéneas en posición\(i\)”. Aquí está:\(U_i\) Sea el subconjunto\(\mathbb{F}\mathbb{P}_n\) de puntos cuya coordenada homogénea\(x_i\) es distinta de cero. Que\ (\ pi_i\ colon u_i\ a
\ mathbb {F} ^n\) sea dado por

\ begin {ecuación*}
[x_0, x_2,\ ldots x_ {i-1}, x_i, x_ {i+1},\ ldots, x_n]
\ a\ izquierda (\ frac {x_0} {x_i},\ frac {x_2} {x_i},\ ldots
\ frac {x_ {i-1}} {x_i},\ frac {x_ {i+1}} {x_i},\ ldots,\ frac {x_n} {x_i}\ derecha).
\ end {ecuación*}

El inverso unilateral\(\mathbb{F}^n\to \mathbb{F}\mathbb{P}_n\) dado por

\ begin {ecuación*}
(x_0, x_1,\ ldots x_ {i-1},\ anchohat {x_i}, x_ {i+1},\ ldots, x_n)
\ a [x_0, x_1,\ lpuntos x_ {i-1} ,1, x_ {i+1},\ ldots, x_n]
\ end {ecuación*}

(donde el sombrero circunfleja indica un elemento eliminado de una secuencia) se llama el\(i\) -ésimo gráfico de coordenadas para\(\mathbb{F}\mathbb{P}_n\text{.}\) ¿Cuál es el mapa que resulta de aplicar el\(0\) -ésimo gráfico de coordenadas\(\mathbb{C}\to \mathbb{C}\mathbb{P}_2\) seguido de tomar coordenadas homogéneas en posición\(1\)?

Ejercicio 3: La geometría de Möbius es geometría proyectiva

Mostrar que la geometría de Möbius\((\hat{\mathbb{C}},\mathbf{M})\) y la geometría proyectiva\((\mathbb{P}(\mathbb{C}^2),PGL(2))\) son equivalentes a través del mapa\(\mu\colon \mathbb{P}(\mathbb{C}^2) \to \hat{\mathbb{C}}\) dado por

\ begin {ecuación}
\ mu ([\ alpha,\ beta]) =\ left\ {
\ begin {array} {cc}
\ alpha/\ beta &\ beta\ neq 0\\
\ infty &\ beta=0
\ end {array}
\ right.. \ label {mobiusmodelequivmap}\ tag {3.5.3}
\ end {ecuación}

Comentario: Observe que\(\mu\) es una extensión de\ (\ pi_1\ colon
U_1\ a\ mathbb {C}\) dada por\(\pi_1([x_0,x_1])=\frac{x_0}{x_1}\) (definida en el Ejercicio 3.5.5.2).

Ejercicio 4: Relación cruzada

El espacio proyectivo\(\mathbb{P}_1=\mathbb{P}(\mathbb{F}^2)\) se llama la línea proyectiva). El mapa\(\mu\colon \mathbb{P}_1\to \hat{\mathbb{F}}\text{,}\) dado por\(\mu([x_0,x_1])=\frac{x_0}{x_1}\) (definido en el Ejercicio 3.5.5.3, pero donde\(\mathbb{F}\) puede haber cualquier campo, con\(\hat{\mathbb{F}}=\mathbb{F}\cup \{\infty\}\)) toma los puntos

\ begin {ecuación*}
[e_0] = [1,1], [e_2] = [0,1], [e_1] = [1,0]
\ final {ecuación*}

en\(\mathbb{P}_1\) a los puntos\(1,0,\infty\) en\(\hat{\mathbb{F}}\text{,}\) respectivamente. Dejar\((\cdot,P_1,P_2,P_3)\) denotar la transformación proyectiva única\([T]\) que lleva\(P_1,P_2,P_3\) a\([e_0],[e_2],[e_1]\text{.}\) La relación cruzada\((P_0,P_1,P_2,P_3)\) se define para ser\(\mu([T](P_0))\text{.}\)).

1. Demostrar que esta definición de relación cruzada en geometría proyectiva corresponde a la relación cruzada de la geometría de Möbius para el caso\(\mathbb{F}=\mathbb{C}\text{,}\) a través del mapa es\(\mu\text{,}\) decir, mostrar que lo siguiente sostiene.

   \ begin {ecuación*}
   (P_0, P_1, P_2, P_3) =(\ mu (P_0),\ mu (P_1),\ mu (P_2),\ mu (P_3))
   \ end {ecuación*}

2. Demostrar que

   \ (\ begin {ecuación*}
   (P_0, P_1, P_2, P_3) =\ frac {\ det (P_0P_2)\ det (P_1P_3)} {\ det (P_1P_2)\ det (P_0P_3)}
   \ end {ecuación*}\)

   donde\(\det(P_iP_j)\) esta el determinante de la matriz\ (\ begin {bmatrix}
   {a_i} & {a_j}\\
   {b_i} & {b_j}
   \ end {bmatrix}\ text {,}\) donde\(P_i=[a_i,b_i]\text{.}\)

Ejercicio 5: Condición para la colinealidad en RP2

Dejar\(u=(u_1,u_2,u_3),v=(v_1,v_2,v_3),w=(w_1,w_2,w_3)\) ser vectores adentro\(\mathbb{R}^3\text{,}\) y dejar\(M\) ser la matriz\ (M=\ left [\ begin {array} {ccc}
u_1 & v_1 & w_1\\
u_2 & v_2 & w_2\\
u_3 & v_3 & w_3\\ end {array}\ right]\) Mostrar que\([u],[v],[w]\) son colineales en\(\mathbb{R}\mathbb{P}_2\) si y solo si \(\det M=0\text{.}\)

Figura 3.5.5. Teorema de Pappus

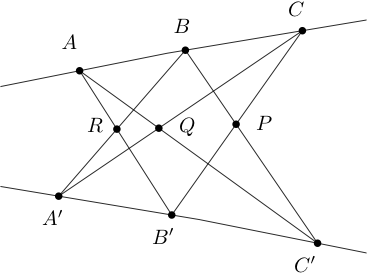
El siguiente es un famoso teorema de la geometría clásica.

Ejercicio 6: Teorema de Pappus

Let\(A,B,C\) be tres puntos colineales distintos en\(\mathbb{R}\mathbb{P}_2\text{.}\) Let\(A',B',C'\) be otros tres puntos colineales distintos en una línea diferente. Dejar\(P,Q,R\) ser los puntos de intersección\(P=BC'\cap B'C\text{,}\)\ (Q=AC'\ cap
A'C\ text {,}\)\(R=AB'\cap A'B\text{.}\) Entonces los puntos\(P,Q,R\) son colineales. Ver Figura 3.5.5.

Siga el esquema a continuación para probar el Teorema de Pappus bajo la suposición adicional de que no tres de\(\) A, A′, P, R son colineales. Aplicando el Teorema Fundamental de la Geometría Proyectiva, podemos asumir\(A=[e_1]\text{,}\)\(A'=[e_2]\text{,}\)\(P=[e_3]\text{,}\) y\(R=[e_0]\text{.}\)

• Verifica eso\(AR=[0,-1,1]\) y\(A'R=[1,0,-1]\text{.}\)
• Explique por qué se deduce eso\(B'=[r,1,1]\) y\(B=[1,s,1]\) para algunos\(r,s\text{.}\)
• Explicar por qué\(C=[rs,s,1]\) y\(C'=[r,rs,1]\text{.}\)
• Explicar por qué\(Q=[rs,rs,1]\text{.}\)
• Observe que\(P,Q,R\) todos se encuentran en\([1,-1,0]\text{.}\)

Pista

Para el segundo punto de viñeta, use el hecho de que\(B'=[x,y,z]\) se encuentra\(AR\)\(y=z\text{.}\) para obtener Para el tercer punto de viñeta, use coordenadas conocidas\(A,B,B',P\) para para obtener coordenadas para líneas\(AB,PB'\text{.}\) Luego\(C= AB\cap PB'\text{.}\) Use un proceso similar para\(C'\text{.}\) Cuatro la cuarta viñeta, use\(Q=AC'\times A'C\text{.}\)

Ejercicio 7: Cuadricos

Un quadric in\(\mathbb{P}(\mathbb{F}^{n+1})\) es un conjunto de puntos cuyas coordenadas homogéneas satisfacen una ecuación de la forma

\ begin {ecuación}
\ suma_ {0\ leq i\ leq j\ leq n} c_ {ij} x_ix_j=0. \ label {cuadriceqn}\ tag {3.5.4}
\ end {ecuación}

Un quadric in\(\mathbb{R}\mathbb{P}_2\) se llama cónico.

1. Explique por qué (3.5.4) es una definición legítima de un conjunto de puntos en\(\mathbb{P}(\mathbb{F}^{n+1})\text{.}\)
2. Considera la cónica\(C\) dada por

   \ begin {ecuación*}
   x_0^2+x_1^2 -x_2^2=0.
   \ end {ecuación*}

   ¿Cuáles son las cifras en\(\mathbb{R}^2\) ese resultado de tomar coordenadas no homogéneas (ver Ejercicio 3.5.5.2)\(C\) en posiciones\(0,1,2\text{?}\)