3.6: Ejercicios adicionales

Ejercicios

Ejercicio 1

Subgrupo euclidiano del grupo Möbius.

Dejar\(\mathbf{E}\) denotar el subgrupo del grupo Möbius\(\mathbf{M}\) generado por rotaciones y traslaciones, es decir, transformaciones del tipo\(z\to e^{it}z\) para\(t\in \mathbb{R}\) y\(z\to z+b\) para\(b\in C\text{.}\) La geometría a veces\((\mathbb{C},\mathbf{E})\) se llama “geometría euclidiana”. ¿\((\mathbb{C},\mathbf{E})\)Equivale a la geometría euclidiana definida en la Subsección 3.1.1? ¿Por qué o por qué no?

Ejercicio 2

Geometría elíptica y geometría esférica.

¿La geometría elíptica es\((\hat{\mathbb{C}},\mathbf{S})\) equivalente a la geometría esférica definida en la Subsección 3.1.1? ¿Por qué o por qué no?

Ejercicio 3

Desplazamientos paralelos en geometría hiperbólica.

Dejar\(T\) ser un elemento del grupo hiperbólico\(\mathbf{H}\), con un solo punto fijo\(p\) y forma normal

\ begin {ecuación*}
\ frac {1} {tz-p} =\ frac {1} {1-p} +\ beta.
\ end {ecuación*}

\(p\beta\)Demostrar que debe ser un número imaginario puro, es decir, debe haber un número real\(k\) tal que\(p\beta=ki\text{.}\)

Ejercicio 4

Demostrar que todos los elementos del grupo elíptico\(\mathbf{S}\) son elípticos en el sentido de forma normal, es decir, tenemos\(|\alpha|=1\) en la expresión de forma normal

\ begin {ecuación*}
\ frac {tz-p} {tz-q} =\ alpha
\ frac {z-p} {z-q}.
\ end {ecuación*}

Sugerencia: Primero encuentre los puntos fijos\(p,q\text{,}\) luego ponga\(z=\infty\) en la ecuación de forma normal y resuelva para\(\alpha\text{.}\)

Ejercicio 5

Derivación alternativa de la fórmula para elementos de grupos elípticos.

Para obtener una fórmula explícita para los elementos del grupo elíptico, comenzamos con una condición necesaria. Sea\ (r=s^ {-1}\ circ
T\ circ s\) la rotación de\(S^2\) esos levantamientos\(T\) vía proyección estereográfica. Si\(P,Q\) hay un par de puntos finales de un diámetro de\(S^2\text{,}\) entonces también\(R(P),R(Q)\) debe ser un par de puntos finales de un diámetro. El ejercicio 1.3.3.7 establece la condición de que dos números complejos\(p,q\) sean proyecciones estereográficas de puntos finales de un diámetro si y solo si\(pq^\ast = -1\text{.}\) Así tenemos la siguiente condición necesaria para\(T\text{.}\)

\ begin {ecuación}
pq^\ ast = -1\;\;\ text {implica}\;\; Tp (Tq) ^\ ast =
-1\ label {diamendpreservecond}\ tag {3.6.1}
\ end {ecuación}

Ahora supongamos que\(Tz=\frac{az+b}{cz+d}\) con\(ad-bc=1\text{.}\) Resolver la ecuación
\ (Tp =\ frac {-1} {(T (\ frac {-1} {p^\ ast})) ^\ ast}\) lleva a\(c=-b^\ast\) y\(d=a^\ast\text{.}\) así concluimos que\(T\) tiene la siguiente forma.

\ begin {ecuación}
Tz=\ frac {az+b} {-b^\ ast z+a^\ ast},\;\; |a|a|^2+|b|^2=1\ label {elípticatranssu2form}\ tag {3.6.2}
\ end {ecuación}

Realizar el cómputo a derivar (3.6.2). Explique por qué no hay pérdida de generalidad asumiendo\(ad-bc=1\text{.}\)

Ejercicio 6

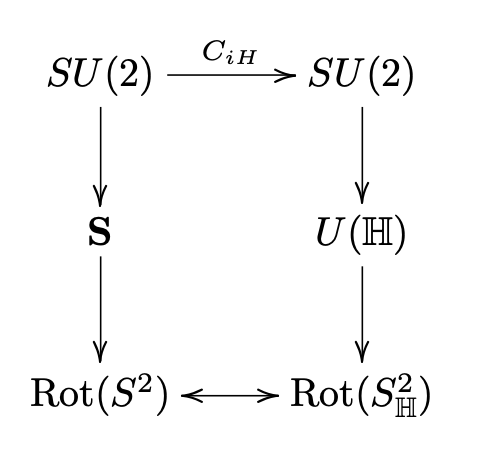
Identificaciones de U (H) y S con Rot (S2).

La discusión de la geometría elíptica (Sección 3.4) establece dos formas de construir rotaciones a partir de matrices. El propósito de este ejercicio es conciliar estas identificaciones. Dado\(a,b\in \mathbb{C}\) con\(|a|^2+|b|^2=1\text{,}\) vamos a definir los siguientes objetos, todos parametrizados por\(a,b\text{.}\)

\ begin {alinear*}
M_ {a, b} & =\ left [\ begin {array} {cc} {a} &
{b}\\ {-b^\ ast} & {a^\ ast}\ end {array}\ derecha]\\
r_ {a, b} & = Re (a) +Im (a) I+Re (b) J+im (b) k\\
R_ {r_ {a, b}} & =\ izquierda [u\ a
r_ {a, b} ur_ {a, b} ^\ ast\ derecha]\;\;\ texto {para} u\ en S^2_\ mathbb {H}\\
T_ {a, b} & =\ izquierda [z\ a\ frac {az+b} {-b^\ ast
z+a^\ ast}\ derecha]\;\;\ texto {para} z\ in\ hat {\ mathbb {C}}\\
R_ {T_ {a, b}} & = s^ {-1}\ circ T_ {a, b}\ circ s
\ final {alinear*}

Los objetos anteriores están organizados a lo largo de dos secuencias de mapeos. La rotación\(R_{r_{a,b}}\) está al final del “camino del cuaternión”

\ begin {align}
SU (2) &\ a U (\ mathbb {H})\ a Rot (S^2_\ mathbb {H})\ label {quatpath}\ tag {3.6.3}\\
M_ {a, b} &
\ a r_ {a, b}\ a R_ {r_ {a, b}}\ notag
\ end {align}

y la rotación\(R_{T_{a,b}}\) está al final del “camino de Möbius”

\ begin {align}
SU (2) &\ a\ S\ a Rot (S^2)\ label {mobiuspath}\ tag {3.6.4}\\
M_ {a, b} &
\ a T_ {a, b}\ a R_ {T_ {a, b}}. \ noetiqueta
\ end {align}

Este problema se trata de comparar las rotaciones\(R_{r_{a,b}}\) y\(R_{T_{a,b}}\) (ver Cuadro 3.6.1) y conciliar la diferencia. Los ángulos de rotación son los mismos, pero los ejes son diferentes, pero sólo por un reordenamiento de coordenadas y un signo menos.

Cuadro 3.6.1. Eje y ángulo de rotación para construcciones de rotación de cuaternión y Möbius

\(R_{v,\theta}\)	eje de rotación\(v\)	ángulo de rotación\(\theta\)
\(R_{r_{a,b}}\)	\(\frac{(Im(a),Re(b),Im(b))}{\sqrt{1-(Re(a))^2}}\)	\(2\arccos(Re(a))\)
\(R_{T_{a,b}}\)	\(\frac{(Im(b),-Re(b),Im(a))}{\sqrt{1-(Re(a))^2}}\)	\(2\arccos(Re(a))\)

Los ejercicios que se detallan a continuación verifican los valores para\(v,\theta\) el Cuadro 3.6.1.

1. Utilice la Proposición 1.2.9 para justificar los valores para\(v\) y\(\theta\) para\(R_{r_{a,b}}\) en el Cuadro 3.6.1.
2. Resuelve\(T_{a,b}z=z\) demostrar que uno de los puntos fijos de\(T_{a,b}\) es

   \ begin {ecuación*}
   p=-ib\ izquierda (\ frac {\ sqrt {1- (Re (a)) ^2} + Im (a)} {|b|^2}\ derecha).
   \ end {ecuación*}

3. Demostrar que\(s\left(\frac{(Im(b),-Re(b),Im(a))}{\sqrt{1-(Re(a))^2}}\right)=p\text{.}\)
4. Demostrar que

   \ begin {ecuación}
   T_ {a, b} = s\ circ h\ circ R_ {r_ {a, b}}\ circ h\ circ s^ {-1}\ label {trhcommute}\ tag {3.6.5}
   \ end {ecuación}

   donde\(h\colon \mathbb{R}^3\to \mathbb{R}^3\) se da por\((x,y,z)\to (z,-y,z)\text{.}\) Aquí hay una manera de hacer esto: evaluar ambos lados de (3.6.5) en los tres puntos ¡\(p,0,\infty\text{.}\)Explica por qué esto es suficiente! Utilizar la multiplicación de cuaterniones\(R_{r_{a,b}}\text{.}\) para evaluar Por ejemplo,\(R_{r_{a,b}}(1,0,0)=r_{a,b}ir_{a,b}^\ast\) bajo la identificación natural\(\mathbb{R}^3\leftrightarrow \mathbb{R}^3_\mathbb{H}\text{.}\)
5. Aquí hay una manera de conciliar el camino del cuaternión (3.6.3) con el camino de Möbius (3.6.4). Dejar\ (H=\ frac {1} {\ sqrt {2}}\ left [\ begin {array} {cc}
   1& 1\\ 1& -1\ end {array}\ right]\) (la matriz a veces\(H\) se llama la matriz Hadamard) y vamos\(C_{iH}\) denotar el mapa\(M\to (iH)M(iH)^{-1}\text{.}\) Mostrar que el diagrama en la Figura 3.6.2 conmuta. Pista: Observe eso\(iH\in SU(2)\) y eso\(Q(iH)=\frac{1}{\sqrt{2}}(i+k)\text{,}\) y eso\(R_{Q(iH)}=h\text{.}\)

Figura 3.6.2. El mapa\(C_{iH}\) viene dado por\(C_{iH}(T)=(iH)T(iH)^{-1}\text{.}\) La columna de mapas de la izquierda es el “camino de Möbius”, y la columna de mapas a la derecha es el “camino del cuaternión”.

Figura 3.6.3. Triángulo recto\(\triangle ABC\)

Ejercicio 7

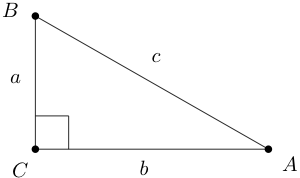
Teoremas de Pitágoras.

Dejar\(\triangle ABC\) ser un triángulo rectángulo con ángulo recto\(\angle C\) con longitudes laterales\(a=d(B,C)\text{,}\)\(b=d(A,C)\text{,}\) y\(c=d(A,B)\) para que la longitud de la hipotenusa sea\(c\text{.}\) Ver Figura 3.6.3.

1. Demostrar las siguientes identidades.

   \ begin {align}
   \ cosh\ left (\ ln\ left (\ frac {1+u} {1-u}\ right)\ right) & =
   \ frac {1+u^2} {1-u^2}\;\ ;( 0\ lt u\ lt 1)\ label {coshhyperbolicdistidentity}\ tag {3.6.6}\\
   \ cos (2\ arctan u) & =\ frac {1-u^2} {1+u^2}\ etiqueta {cosellipticistidentidad}\ etiqueta {3.6.7}
   \ end {align}

2. El Teorema de Pitágoras Hiperbólicas. Demostrar que

   \ begin {ecuación}
   \ cosh (c) =\ cosh (a)\ cosh (b)\ label {hyperbolicpitagthm}\ tag {3.6.8}
   \ end {ecuación}

   si\(T\) es un triángulo hiperbólico.
3. El Teorema de Pitágoras Elípticas. Demostrar que

   \ begin {ecuación}
   \ cos (c) =\ cos (a)\ cos (b)\ label {elipticpitagthm}\ tag {3.6.9}
   \ end {ecuación}

   if\(T\) es un triángulo elíptico.

Sugerencia: Utilizar una transformación para colocar\(C\) en\(0\) in\(\mathbb{D}\) o\(\hat{\mathbb{C}}\), con\(A\) es real y\(B\) puro imaginario. Usa la fórmula\ (d (p, q) =
\ ln ((1+u)/(1-u))\) con\(u=\left|\frac{q-p}{1-p^\ast q}\right|\) para la distancia hiperbólica. Usa la fórmula\ (d (p, q) =
2\ arctan (u)\ text {,}\) con\ (u=\ izquierda|\ frac {q-p} {1+p^\ ast
q}\ derecha|\) para distancia elíptica. Las identidades de parte\((a)\) serán útiles.