2.1: Simetría y funciones
- Page ID
- 111044
Ahora trabajaremos hacia una definición precisa de un grupo. En matemáticas, a menudo comenzamos exploraciones con algún concepto general (en nuestro caso, simetría) y luego trabajamos sobre esos conceptos hasta llegar a una definición muy precisa. Tener definiciones precisas nos permite mejores abstracciones y generalizaciones; cuanto más precisas sean nuestras definiciones, mejores serán las matemáticas que podemos esperar derivar.
Recordemos nuestra definición de las simetrías de un objeto geométrico: todas las formas de mover ese objeto de nuevo sobre sí mismo sin cambiarlo. Cada una de estas diferentes formas de mover el objeto de nuevo sobre sí mismo podemos identificar como una función. Llamemos a nuestro objeto\(X\). Then every symmetry of \(X\) we can identify as a certain special function \(f:X\rightarrow X\).
Anteriormente señalamos que dejando\(X\) alone should also be a symmetry of \(X\). This is the identity function! \(id:X\rightarrow X\), with \(id(x)=x\) for all points \(x\in X\).
A continuación, notamos que la composición de funciones es una operación útil: De hecho, si tenemos dos simetrías diferentes\(f\) and \(g\) of \(X\), then their composition \(g\circ f\) will also be a symmetry. The first function applied to \(X\) 'moves \(X\) onto itself without changing it,' and then the second does as well. Thus, the composition is also a symmetry.
Finalmente, observamos de pasada que la composición de funciones es asociativa: para tres simetrías\(f,g,h\), we have \((f\circ g)\circ h = f\circ (g\circ h)\).
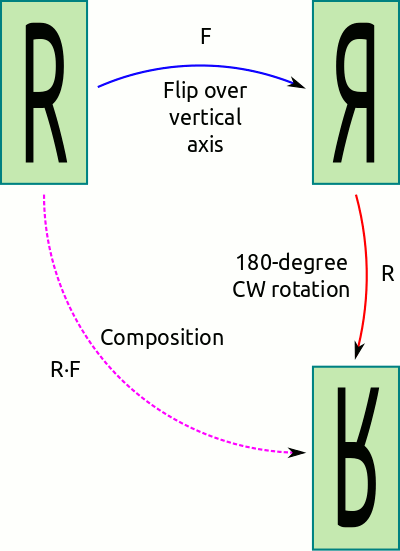
Composición de dos simetrías de un rectángulo.
¡Realmente necesitamos algunos ejemplos aquí! Entonces consideremos la cara perfectamente simétrica. Solo hay dos simetrías: la identidad y el giro de izquierda a derecha (reflexión sobre el eje vertical). Llamar a la identidad\(e\) and the flip \(f\). Then we see that, considered as functions from the face to itself, \(f\circ f=e\).
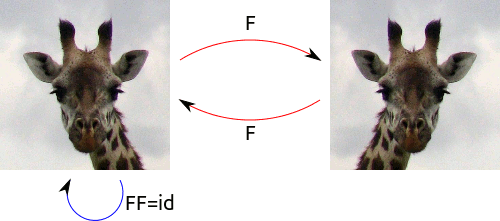
Las flechas rojas describen el giro sobre el eje vertical. Hazlo dos veces, y terminas donde empezaste:\(F\circ F=id\).
Ahora recuerda nuestro hexágono 'accidentado', que sólo tenía simetrías rotacionales. Llamar a la identidad\(e\) and let \(r\) be the clockwise rotation by \(60^\circ\). All of the other rotations we can think of as \(r\) composed with itself some number of times; we'll just write this as \(r^k\). So all of the symmetries of the bumpy hexagon are \(\{e, r, r^2, r^3, r^4, r^5\}\). We notice that \(r^5\circ r=r^6=e\). This is quite interesting! In fact, we can make a 'composition table' to keep track of what happens when we compose any two of the symmetries.
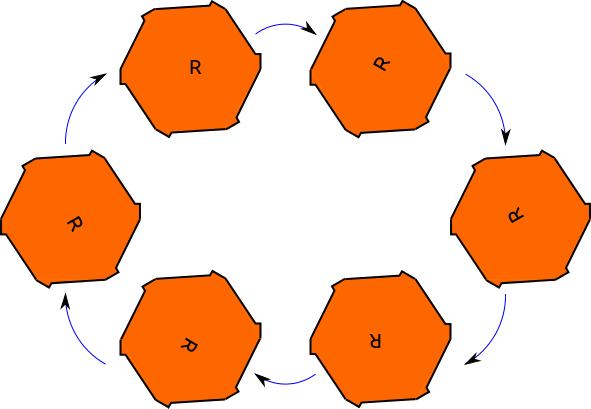
Las seis simetrías rotacionales del hexágono accidentado. La flecha azul representa la rotación\(r\); \(r^6=id\).
And now we can make a slightly less obvious observation: For any of these functions, we can find another symmetry taking the object 'back' to its original orientation. Thus, for any symmetry \(f\), there exists a \(g\) such that \(f\circ g=e\). The function \(g\) is then called the inverse of \(f\). We've already seen two examples of this.


