19.3: Introducción a los modelos de Markov

Última actualización
Guardar como PDF

Page ID: 115270

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

from urllib.request import urlretrieve

urlretrieve('https://raw.githubusercontent.com/colbrydi/jupytercheck/master/answercheck.py', 
            'answercheck.py');

En teoría de probabilidad, un modelo de Markov es un modelo estocástico utilizado para modelar sistemas que cambian aleatoriamente. Se supone que los estados futuros dependen únicamente del estado actual, no de los hechos ocurridos antes de él.

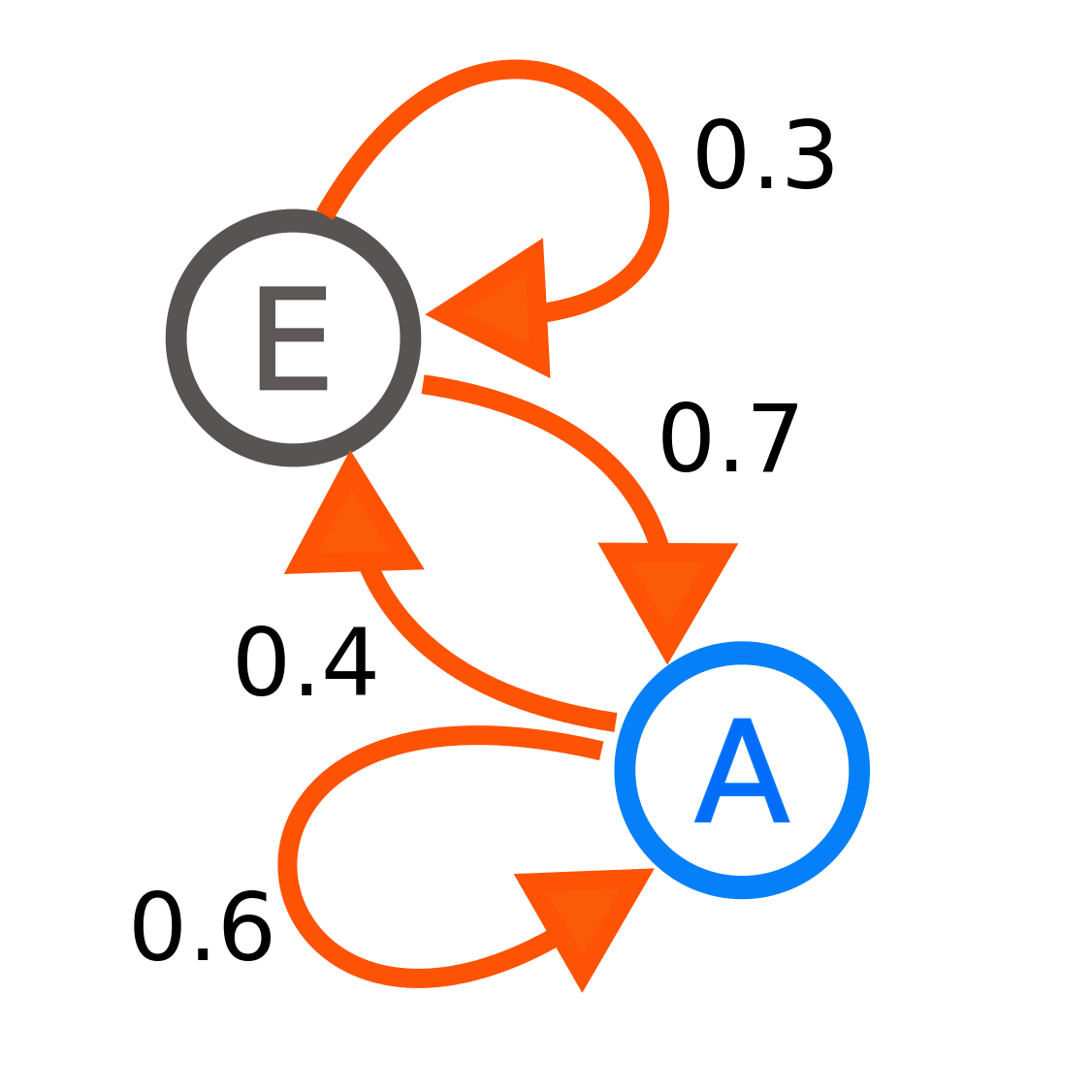
Un modelo de Markov. — Un diagrama que representa un proceso de Markov de dos estados, con los estados etiquetados E y A. Vía Wikipedia

Cada número representa la probabilidad de que el proceso de Markov cambie de un estado a otro, con la dirección indicada por la flecha. Por ejemplo, si el proceso de Markov está en el estado A, entonces la probabilidad de que cambie al estado E es 0.4, mientras que la probabilidad de que permanezca en el estado A es 0.6.

El modelo de estado anterior puede ser representado por una matriz de transición.

En cada paso de tiempo (\(t\)) la probabilidad de moverse entre estados depende del estado anterior (\(t−1\)):

\[A_{t} = 0.6A_{(t-1)}+0.7E_{(t-1)} \nonumber \]

\[E_{t} = 0.4A_{(t-1)}+0.3E_{(t-1)} \nonumber \]

El modelo de estado anterior (\(S_t = [A_t, E_t]^T\)) se puede representar en la siguiente notación matricial:

\[S_t = PS_{(t-1)} \nonumber \]

Hacer esto

Crear una\(2 \times 2\) matriz (P) que represente la matriz de transición para el espacio Markov anterior.

#Put your answer to the above question here

from answercheck import checkanswer

checkanswer.matrix(P,'de1c99f4b4a8d7ea541a084d836ba7e4');