3.4: Propiedades de las funciones continuas
- Page ID
- 107856
Recordemos de la Definición 2.6.3 que un subconjunto\(A\) de\(\mathbb{R}\) es compacto si y solo si cada secuencia\(\left\{a_{n}\right\}\) en\(A\) tiene una subsecuencia\(\left\{a_{n_{k}}\right\}\) que converge a un punto\(a \in A\).
Dejar\(D\) ser un subconjunto compacto no vacío de\(\mathbb{R}\) y dejar\(f: D \rightarrow \mathbb{R}\) ser una función continua. Entonces\(f{D}\) es un subconjunto compacto de\(\mathbb{R}\). En particular,\(f(D)\) está cerrado y acotado.
- Prueba
-
Tome cualquier secuencia\(\left\{y_{n}\right\}\) en\(f(D)\). Entonces para cada uno\(n\), existe\(a_{n} \in D\) tal que\(y_{n}=f\left(a_{n}\right)\). Dado que\(D\) es compacto, existe una subsecuencia\(\left\{a_{n_{k}}\right\}\) de\(\left\{a_{n}\right\}\) y un punto\(a \in D\) tal que
\[\lim _{k \rightarrow \infty} a_{n_{k}}=a \in D .\]
Ahora se deduce del Teorema 3.3.3 que
\[\lim _{k \rightarrow \infty} y_{n_{k}}=\lim _{k \rightarrow \infty} f\left(a_{n_{k}}\right)=f(a) \in f(D) .\]
Por lo tanto,\(f(D)\) es compacto.
La conclusión final se desprende del Teorema 2.6.5\(\square\)
Decimos que la función\(f: D \rightarrow \mathbb{R}\) tiene un mínimo absoluto en\(\bar{x} \in D\) si
\[f(x) \geq f(\bar{x}) \text { for every } x \in D.\]
De igual manera, decimos que\(f\) tiene un máximo absoluto en\(\bar{x}\) si
\[f(x) \leq f(\bar{x}) \text { for every } x \in D.\]
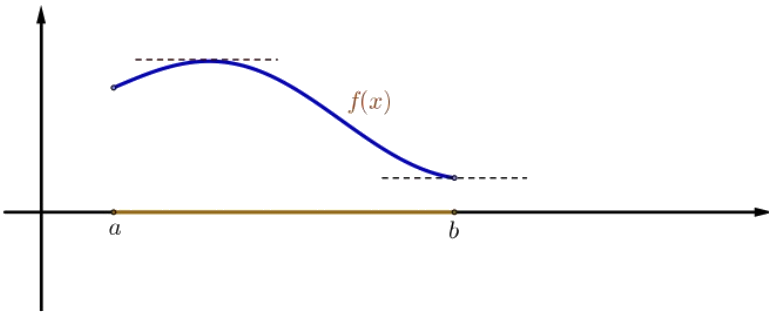
Figura\(3.2\): Máximo absoluto y mínimo absoluto de\(f\) on\([a, b]\).
Supongamos que\(f: D \rightarrow \mathbb{R}\) es continuo y\(D\) es un conjunto compacto. Entonces\(f\) tiene un mínimo absoluto y un máximo asolute encendido\(D\).
- Prueba
-
Ya que\(D\) es compacto,\(A=f(D)\) está cerrado y acotado (ver Teorema 2.6.5). Vamos
\[m=\inf A=\inf _{x \in D} f(x).\]
En particular,\(m \in \mathbb{R}\). Por cada\(n \in \mathbb{N}\), existe\(a_{n} \in A\) tal que
\[m \leq a_{n}<m+1 / n.\]
Para cada uno\(n\), ya que\(a_{n} \in A=f(D)\), existe\(x_{n} \in D\) tal que\(a_{n}=f\left(x_{n}\right)\) y, de ahí,
\[m \leq f\left(x_{n}\right)<m+1 / n.\]
Por la compacidad de\(D\), existe un elemento\(\bar{x} \in D\) y una subsecuencia\(\left\{x_{n_{k}}\right\}\) que converge a\(\bar{x} \in D\) as\(k \rightarrow \infty\). Porque
\[m \leq f\left(x_{n_{k}}\right)<m+\frac{1}{n_{k}} \text { for every } k\]
por el teorema squeeze (Teorema 2.1.6) concluimos\(\lim _{k \rightarrow \infty} f\left(x_{n_{k}}\right)=m\). Por otro lado, por continuidad tenemos\(\lim _{k \rightarrow \infty} f\left(x_{n_{k}}\right)=f(\bar{x})\). Concluimos que\(f(\bar{x})=m \leq f(x)\) para cada\(x \in D\). Así,\(f\) tiene un mínimo absoluto en\(\bar{x}\). La prueba es similar para el caso de máximo absoluto. \(\square\)
La prueba del Teorema 3.4.2 se puede acortar aplicando el Teorema 2.6.4. Sin embargo, hemos proporcionado una prueba directa en su lugar.
Si\(f:[a, b] \rightarrow \mathbb{R}\) es continuo, entonces tiene un mínimo absoluto y un máximo absoluto encendido\([a, b]\).
- Prueba
-
Agrega prueba aquí y automáticamente se ocultará
El corolario 3.4.4 a veces se conoce como el Teorema del Valor Extremo. Se deduce inmediatamente del Teorema 3.4.2, y el hecho de que el intervalo\([a, b]\) es compacto (ver Ejemplo 2.6.4).
El siguiente resultado es una propiedad básica de funciones continuas que se utiliza en una variedad de situaciones.
Dejar\(f: D \rightarrow \mathbb{R}\) ser continuo en\(c \in D\). Supongamos\(f(c) > 0\). Entonces existe\(\delta > 0\) tal que
\[f(x)>0 \text { for every } x \in B(c ; \delta) \cap D.\]
- Prueba
-
Vamos\(\varepsilon=f(c)>0\). Por la continuidad de\(f\) at\(c\), existe\(\delta > 0\) tal que\(x \in D\) y\(|x-c|<\delta\), entonces
\(|f(x)-f(c)|<\varepsilon\).
Esto implica, en particular, que\(f(x)>f(c)-\varepsilon=0\) para cada\(x \in B(c ; \delta) \cap D\). La prueba ya está completa. \(\square\)
Un resultado análogo se mantiene si\(f(c)<0\).
Dejar\(f:[a, b] \rightarrow \mathbb{R}\) ser una función continua. Supongamos\(f(a) \cdot f(b)<0\) (esto significa cualquiera\(f(a)<0<f(b) \text { or } f(a)>0>f(b)\)). Entonces existe\(c \in (a,b)\) tal que\(f(c)=0\).
- Prueba
-
Solo probamos el caso\(f(a)<0<f(b)\) (el caso\(f(a)>0>f(b)\) es completamente análogo). Definir
\[A=\{x \in[a, b]: f(x) \leq 0\} .\]
Este conjunto no está vacío desde\(a \in A\). Este conjunto también está acotado desde\(A \subset[a, b]\). Por lo tanto,\(c=\sup A\) existe y\(a \leq c \leq b\). Eso lo vamos a demostrar\(f(c)=0\) demostrando\(f(c)<0\) y\(f(c)>0\) llevando a contradicciones.
Supongamos\(f(c)<0\). Entonces existe\(\delta > 0\) tal que
\[f(x)<0 \text { for all } x \in B(c ; \delta) \cap[a, b] .\]
Porque\(c<b\) (desde\(f(b)>0\)), podemos encontrar\(s \in(c, b)\) tal que\(f(s) < 0\) (de hecho\(s=\min \{c+ \delta / 2,(c+b) / 2\}\) va a hacer). Esto es una contradicción porque\(s \in A\) y\(s>c\).
Supongamos\(f(c)>0\). Entonces existe\(\delta > 0\) tal que
\[f(x)>0 \text { for all } x \in B(c ; \delta) \cap[a, b] .\]
Ya que\(a<c\) (porque\(f(a)<0\)), existe\(t \in(a, c)\) tal que\(f(x)>0\) para todos\(x \in(t, c)\) (de hecho,\(t=\max \{c-\delta / 2,(a+c) / 2\}\) va a hacer). Por otro lado, ya que\(t<c=\sup A\), existe\(t^{\prime} \in A\) con\(t<t^{\prime} \leq c\). Pero entonces\(t<t^{\prime}\) y\(f\left(t^{\prime}\right) \leq 0\). Esto es una contradicción. Concluimos que\(f(c)=0\). \(\square\)
Dejar\(f:[a, b] \rightarrow \mathbb{R}\) ser una función continua. Supongamos\(f(a)<\gamma<f(b)\). Entonces existe un número\(c \in(a, b)\) tal que\(f(c)=\gamma\).
La misma conclusión sigue si\(f(a)>\gamma>f(b)\).
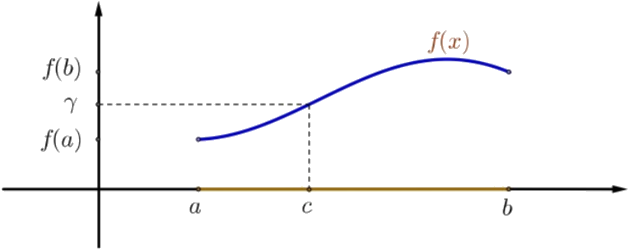
Figura\(3.3\): Ilustración del Teorema del Valor Intermedio.
- Prueba
-
Definir
\[\varphi(x)=f(x)-\gamma, x \in[a, b] .\]
Entonces\(\varphi\) es continuo encendido\([a,b]\). Además,
\[\varphi(a) \varphi(b)=[f(a)-\gamma][f(b)-\gamma]<0 .\]
Por Teorema 3.4.7, existe\(c \in (a,b)\) tal que\(\varphi(c)=0\). Esto equivale a\(f(c)=\gamma\). La prueba ya está completa. \(\square\)
Dejar\(f:[a, b] \rightarrow \mathbb{R}\) ser una función continua. Vamos
\[m=\min \{f(x): x \in[a, b]\} \text { and } M=\max \{f(x): x \in[a, b]\} .\]
Entonces para cada\(\gamma \in[m, M]\), existe\(c \in [a,b]\) tal que\(f(c)=\gamma\).
- Prueba
-
Agrega prueba aquí y automáticamente se ocultará
Utilizaremos el Teorema del Valor Intermedio para demostrar que la ecuación\(e^{x}=-x\) tiene al menos una solución real. Asumiremos conocido que la función exponencial es continua\(\mathbb{R}\) y que\(e^{x}<1\) para\(x<0\).
Solución
Primero defina la función\(f: \mathbb{R} \rightarrow \mathbb{R}\) por\(f(x)=e^{x}+x\). Observe que la ecuación dada tiene una solución\(x\) si y solo si\(f(x)=0\). Ahora, la función\(f\) es continua (como la suma de funciones continuas). Además, tenga en cuenta que\(f(-1)=e^{-1}+(-1)<1-1=0\) y\(f(0)=1>0\). Ahora podemos aplicar el Teorema del Valor Intermedio a la función\(f\) en el intervalo\([-1,0]\) con\(\gamma=0\) para concluir que existe\(c \in [-1,0]\) tal que\(f(c)=0\). El punto\(c\) es la solución deseada a la ecuación original.
Mostramos ahora que, dado\(n \in \mathbb{N}\), cada número real positivo tiene una raíz\(n\) -ésima positiva.
Solución
Dejar\(n \in \mathbb{N}\) y dejar\(a \in \mathbb{R}\) con\(a>0\). Primero observe eso\((1+a)^{n} \geq 1+n a>a\) (ver Ejercicio 1.3.7). Ahora considere la función\(f:[0, \infty) \rightarrow \mathbb{R}\) que le da\(f(x)=x^{n}\). Desde\(f(0)=0\) y\(f(1+a)>a\), se deduce del Teorema del Valor Intermedio que existe\(x \in(0,1+a)\) tal que\(f(x)=a\). Es decir\(x^{n}=a\), como se desee. (Mostramos más adelante en el Ejemplo 4.3.1 que tal\(x\) es único.)
Presentamos a continuación una segunda prueba del Teorema 3.4.8 que no depende del Teorema 3.4.7, sino que, en cambio, se basa en el Teorema de Intervalos Anidados (Teorema 2.3.3).
Construimos una secuencia de intervalos anidados de la siguiente manera. Establecer\(a_{1}=a\),\(b_{1}=b\), y dejar\(I_{1}=[a, b]\). Vamos\(c_{1}=(a+b) / 2\). Si\(f\left(c_{1}\right)=\gamma\), ya terminamos. De lo contrario, ya sea
\ [\ begin {array} {l}
f\ left (c_ {1}\ right) >\ gamma\ quad\ text {o}\\
f\ left (c_ {1}\ right) <\ gamma
\ end {array}.\]
En el primer caso, establecer\(a_{2}=a_{1}\) y\(b_{1}=c_{1}\). En el segundo caso, establecer\(a_{2}=c_{1}\) y\(b_{2}=b_{1}\). Ahora listo\(I_{2}=\left[a_{2}, b_{2}\right]\). Obsérvese que en cualquier caso,
\[f\left(a_{2}\right)<\gamma<f\left(b_{2}\right) .\]
Set\(c_{2}=\left(a_{2}+b_{2}\right) / 2\). Si\(f\left(c_{2}\right)=\gamma\), de nuevo estamos hechos. De lo contrario, ya sea
\ [\ begin {array} {l}
f\ left (c_ {2}\ right) >\ gamma\ quad\ text {o}\\
f\ left (c_ {2}\ right) <\ gamma
\ end {array}.\]
En el primer caso, establecer\(a_{3}=a_{2}\) y\(b_{3}=c_{2}\). En el segundo caso, establecer\(a_{3}=c_{2}\) y\(b_{3}=b_{2}\). Ahora listo\(I_{3}=\left[a_{3}, b_{3}\right]\). Obsérvese que en cualquier caso,
\[f\left(a_{3}\right)<\gamma<f\left(b_{3}\right) .\]
Procediendo de esta manera, o encontramos algunos\(c_{n_{0}}\) tales que\(f\left(c_{n_{0}}\right)=\gamma\) y, por lo tanto, la prueba es completa, o construimos una secuencia de intervalos delimitados cerrados\(\left\{I_{n}\right\}\) con\(I_{n}=\left[a_{n}, b_{n}\right]\) tal que para todos\(n\),
- \(I_{n} \supset I_{n+1}\),
- \(b_{n}-a_{n}=(b-a) / 2^{n-1}\), y
- \(f\left(a_{n}\right)<\gamma<f\left(b_{n}\right)\).
En este caso, procedemos de la siguiente manera. La condición ii) implica que\(\lim _{n \rightarrow \infty}\left(b_{n}-a_{n}\right)=0\). Por el Teorema de Intervalos Anidados (Teorema 2.3.3, parte (b)), existe\(c \in[a, b]\) tal que\(\bigcap_{n=1}^{\infty} I_{n}=\{c\}\). Además, como vemos a partir de la prueba de ese teorema,\(a_{n} \rightarrow c\) y\(b_{n} \rightarrow c\) como\(n \rightarrow \infty\).
Por la continuidad de\(f\), obtenemos
\ [\ begin {array} {l}
\ lim _ {n\ fila derecha\ infty} f\ izquierda (a_ {n}\ derecha) =f (c)\ quad\ texto {y}\\
\ lim _ {n\ fila derecha\ infty} f\ izquierda (b_ {n}\ derecha) =f (c)
\ end {array}.\]
Ya que\(f\left(a_{n}\right)<\gamma<f\left(b_{n}\right)\) para todos\(n\), condición (iii) anterior y Teorema 2.1.5 dan
\ [\ begin {array} {l}
f (c)\ leq\ gamma\ quad\ text {y}\\
f (c)\ geq\ gamma
\ end {array}.\]
De ello se deduce que\(f(c)=\gamma\). Tenga en cuenta que\(f(a)<\gamma<f(b)\), desde entonces\(c \in (a,b)\). La prueba ya está completa. \(\square\)
Ahora vamos a discutir la continuidad de la función inversa. Para una función\(f: D \rightarrow E\), donde\(E\) es un subconjunto de\(\mathbb{R}\), podemos definir la nueva función\(f: D \rightarrow \mathbb{R}\) por la misma notación de función. \(f: D \rightarrow E\)Se dice que la función es continua en un punto\(\bar{x} \in D\) si la función correspondiente\(f: D \rightarrow \mathbb{R}\) es continua en\(\bar{x}\).
Dejar\(f:[a, b] \rightarrow \mathbb{R}\) ser estrictamente creciente y continuo en\([a,b]\). Dejar\(c=f(a)\) y\(d=f(b)\). Entonces\(f\) es uno a uno\(f([a, b])=[c, d]\),, y la función inversa\(f^{-1}\) definida\([c,d]\) por
\[f^{-1}(f(x))=x \text { where } x \in[a, b] ,\]
es una función continua desde\([c,d]\) hacia\([a,b]\).
- Prueba
-
Las dos primeras aseveraciones se derivan de la monotonicidad\(f\) y del Teorema del Valor Intermedio (véase también Corolario 3.4.9). Vamos a demostrar que\(f^{-1}\) es continuo en\([c,d]\). Arreglar cualquiera\(\bar{y} \in [c,d]\) y fijar cualquier secuencia\(\left\{y_{k}\right\}\) en la\([c,d]\) que converja a\(\bar{y}\). Dejar\(\bar{x} \in[a, b]\) y\(x_{k} \in[a, b]\) ser tal que
\[f(\bar{x})=\bar{y} \text { and } f\left(x_{k}\right)=y_{k} \text { for every } k .\]
Entonces\(f^{-1}(\bar{y})=\bar{x}\) y\(f^{-1}\left(y_{k}\right)=x_{k}\) para cada\(k\). Supongamos por contradicción que\(\left\{x_{k}\right\}\) no converge a\(\bar{x}\). Entonces existe\(\varepsilon_{0}>0\) y una subsecuencia\(\left\{x_{k_{\ell}}\right\}\) de\(\left\{x_{k}\right\}\) tal manera que
\[\left|x_{k_{\ell}}-\bar{x}\right| \geq \varepsilon_{0} \text { for every } \ell .\]
Dado que la secuencia\(\left\{x_{k_{\ell}}\right\}\) está acotada, tiene una subsecuencia adicional que converge a\(x_{0} \in[a, b]\). Para simplificar la notación, volveremos a llamar a la nueva subsecuencia\(\left\{x_{k_{\ell}}\right\}\). Tomando límites en (3.7), obtenemos
\[\left|x_{0}-\bar{x}\right| \geq \varepsilon_{0}>0 .\]
Por otro lado, por la continuidad de\(f\),\(\left\{f\left(x_{k_{\ell}}\right)\right\}\) converge a\(f\left(x_{0}\right)\). Ya que\(f\left(x_{k_{\ell}}\right)=y_{k_{\ell}} \rightarrow \bar{y}\) como\(\ell \rightarrow \infty\), se deduce que\(f\left(x_{0}\right)=\bar{y}=f(\bar{x})\). Esto implica\(x_{0}=\bar{x}\), lo que contradice (3.8). \(\square\)
Un resultado similar se mantiene si el dominio de\(f\) es el intervalo abierto\((a,b)\) con algunas consideraciones adicionales. Si\(f:(a, b) \rightarrow \mathbb{R}\) es creciente y acotado, siguiendoen el argumento en el Teorema 3.2.4 podemos demostrar que ambos\(\lim _{x \rightarrow a^{+}} f(x)=c\) y\(\lim _{x \rightarrow b^{-}} f(x)=d\) existen en\(\mathbb{R}\) (ver Ejercicio 3.2.10). Utilizando el Teorema del Valor Intermedio lo obtenemos\(f((a, b))=(c, d)\). Ahora podemos proceder como en el teorema anterior para mostrar que\(f\) tiene una inversa continua de\((c,d)\) a\((a,b)\).
Si\(:(a, b) \rightarrow \mathbb{R}\) es creciente, continuo, acotado por debajo, pero no acotado arriba, entonces\(\lim _{x \rightarrow a^{+}} f(x)= c \in \mathbb{R}\), sino\(\lim _{x \rightarrow b^{-}} f(x)=\infty\) (nuevamente ver Ejercicio 3.2.10). En este caso podemos mostrar usando el Teorema del Valor Intermedio que\(f((a, b))=(c, \infty)\) y podemos proceder como anteriormente para demostrar que\(f\) tiene una inversa continua de\((c, \infty)\) a\((a,b)\).
Las otras posibilidades conducen a resultados similares.
Un teorema similar se puede probar para funciones estrictamente decrecientes.
Ejercicio\(\PageIndex{1}\)
Dejar\(f: D \rightarrow \mathbb{R}\) ser continuo en\(c \in D\) y dejar\(\gamma \in \mathbb{R}\). Supongamos\(f(c)>\gamma\). Demostrar que existe\(\delta>0\) tal que
\[f(x)>\gamma \text { for every } x \in B(c ; \delta) \cap D .\]
- Responder
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{2}\)
Dejar\(f,g\) ser funciones continuas encendidas\([a,b]\). Supongamos\(f(a)<g(a)\) y\(f(b)>g(b)\). Demostrar que existe\(x_{0} \in(a, b)\) tal que\(f\left(x_{0}\right)=g\left(x_{0}\right)\).
Ejercicio\(\PageIndex{3}\)
Demostrar que la ecuación\(\cos x=x\) tiene al menos una solución en\(\mathbb{R}\). (Supongamos que se sabe que la función\(\cos x\) es continua.
Ejercicio\(\PageIndex{4}\)
Demostrar que la ecuación\(x^{2}-2=\cos (x+1)\) tiene al menos dos soluciones reales. (Supongamos que se sabe que la función\(\cos x\) es continua.)
Ejercicio\(\PageIndex{5}\)
Dejar\(f:[a, b] \rightarrow[a, b]\) ser una función continua.
- Demostrar que la ecuación\(f(x)=x\) tiene una solución sobre\([a,b]\).
- Supongamos además que
\[|f(x)-f(y)|<|x-y| \text { for all } x, y \in[a, b], x \neq y .\]
Demostrar que la ecuación\(f(x)=x\) tiene una solución única en\([a,b]\)
Ejercicio\(\PageIndex{6}\)
Dejar\(f\) ser una función continua en\([a,b]\) y\(x_{1}, x_{2}, \ldots, x_{n} \in[a, b]\). Demostrar que existe\(c \in [a,b]\) con
\ [f (c) =\ frac {f\ izquierda (x_ {1}\ derecha) +f\ izquierda (x_ {2}\ derecha) +\ cdots f\ izquierda (x_ {n}\ derecha)} {n} . \
Ejercicio\(\PageIndex{7}\)
Supongamos que\(f\) es una función continua sobre\(\mathbb{R}\) tal que\(|f(x)| < |x| \text { for all } x \neq 0\).
- \(f(0)=0\)Demuéstralo.
- Dados dos números positivos\(a\) y\(b\) con\(a < b\), demostrar que existe\(\ell \in[0,1)\) tal que\[|f(x)| \leq \ell|x| \text { for all } x \in[a, b].\]
Ejercicio\(\PageIndex{8}\)
Dejar\(f, g:[0,1] \rightarrow[0,1]\) ser funciones continuas de tal manera que
\[f(g(x))=g(f(x)) \text { for all } x \in[0,1] . \nonumber\]
Supongamos además que\(f\) es monótona. Demostrar que existe\(x_{0} \in[0,1]\) tal que
\[f\left(x_{0}\right)=g\left(x_{0}\right)=x_{0} . \nonumber\]


