3.8: Juegos Abiertos y Cerrados. Barrios
- Page ID
- 113841
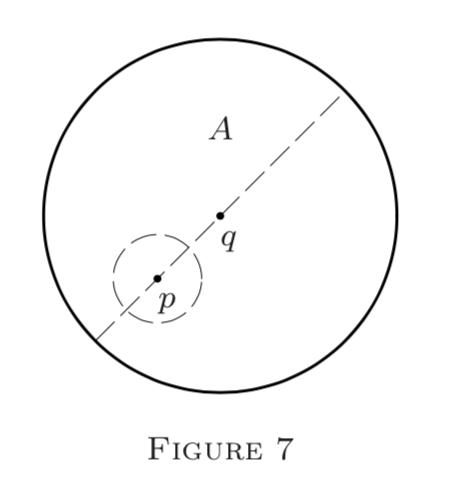
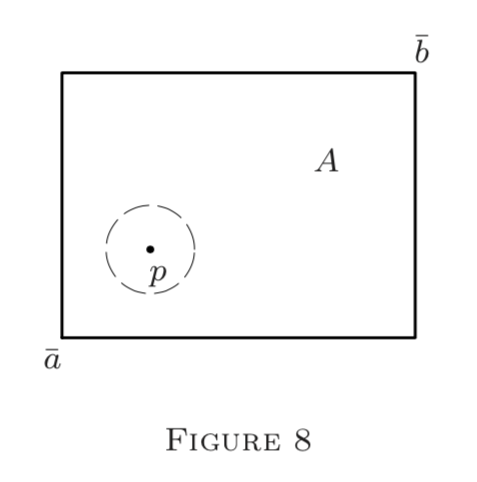
I.\(A\) Sea un globo abierto en\((S, \rho)\) o un intervalo abierto\((\overline{a}, \overline{b})\) en\(E^{n} .\) Entonces cada uno\(p \in A\) puede encerrarse en un globo pequeño\(G_{p}(\delta) \subseteq A(\) Figuras 7 y 8\()\). (Esto fallaría para los puntos de “límite”; pero no hay ninguno dentro de un abierto\(G_{q}\) o\((\overline{a}, \overline{b}) . )\).
Esto sugiere las siguientes ideas, para cualquier\((S, \rho)\).
\(p\)Se dice que un punto es interior a un conjunto\(A \subseteq(S, \rho)\) iff\(A\) contiene algunos\(G_{p} ;\) es decir,\(p,\) junto con algún globo\(G_{p},\) pertenece a\(A .\) Entonces también decimos que\(A\) es un barrio de\(p .\) El conjunto de todos los puntos interiores de\(A\) (“el interior de\(A^{\prime \prime}\) se denota\(A^{0} .\) Nota:\(\emptyset^{0}=\emptyset\) y\(S^{0}=S !\)
\(\mathrm{A}\)conjunto\(A \subseteq(S, \rho)\) se dice que es abierto iff\(A\) coincide con su interior\(\left(A^{0}=A\right) .\) Tales son\(\emptyset\) y\(S .\)
(1) Como se señaló anteriormente, un globo abierto solo\(G_{q}(r)\) tiene puntos interiores, y por lo tanto es un conjunto abierto en el sentido de Definición\(2 .\) (Ver Problema 1 para una prueba.)
(2) Lo mismo se aplica a un intervalo abierto\((\overline{a}, \overline{b})\) en\(E^{n} .\) (Ver Problema\(2 . )\)
(3) El interior de cualquier intervalo en\(E^{n}\) nunca incluye sus puntos finales\(\overline{a}\) y\(\overline{b}\). De hecho, coincide con el intervalo abierto\((\overline{a}, \overline{b}) .\) (Ver Problema\(4 . )\)
(4) El conjunto\(R\) de todos los racionales en no\(E^{1}\) tiene puntos interiores en absoluto\(\left(R^{0}=\emptyset\right)\) porque no puede contener ningún\(G_{p}=(p-\varepsilon, p+\varepsilon) .\) Efectivamente, cualquiera de tales\(G_{p}\) contiene irracionales (ver Capítulo 2, §§11-12, Problema 5\(),\) por lo que no está contenido del todo en\(R .\)
(propiedad de Hausdorff). Dos puntos cualesquiera\(p\) y\(q\)\((p \neq q)\) adentro\((S, \rho)\) son centros de dos globos disjuntos.
Más precisamente,
\[(\exists \varepsilon>0) \quad G_{p}(\varepsilon) \cap G_{q}(\varepsilon)=\emptyset.\]
- Prueba
-
Como\(p \neq q,\) tenemos\(\rho(p, q)>0\) por axioma métrico\(\left(\mathrm{i}^{\prime}\right) .\) Así podemos poner
\[\varepsilon=\frac{1}{2} \rho(p, q)>0.\]
Queda por demostrarlo con esto\(\varepsilon, G_{p}(\varepsilon) \cap G_{q}(\varepsilon)=\emptyset\).
Buscando una contradicción, supongamos que esto falla. Luego está\(x \in G_{p}(\varepsilon) \cap G_{q}(\varepsilon)\) así que\(\rho(p, x)<\varepsilon\) y\(\rho(x, q)<\varepsilon .\) Por la ley del triángulo,
\[\rho(p, q) \leq \rho(p, x)+\rho(x, q)<\varepsilon+\varepsilon=2 \varepsilon ; \text{ i.e., } \rho(p, q)<2 \varepsilon,\]
lo cual es imposible ya que\(\rho(p, q)=2 \varepsilon . \square\)
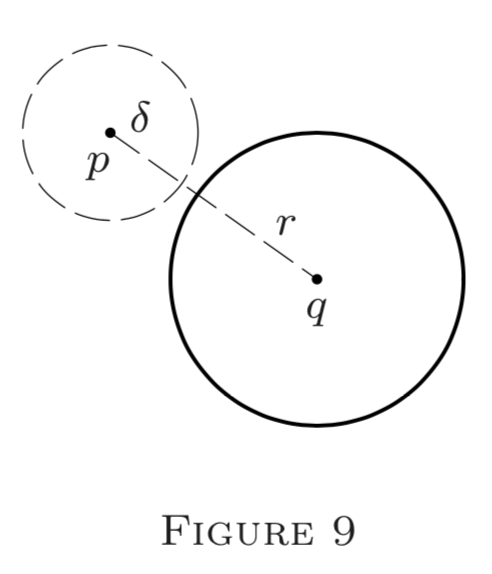
Nota. Una mirada a la Figura 9 explica la idea de esta prueba, es decir, para obtener dos globos disjuntos de igual radio, basta con elegir Se aconseja\(\varepsilon \leq \frac{1}{2} \rho(p, q) .\) al lector que utilice dichos diagramas\(E^{2}\) como guía.
II. Ahora podemos definir conjuntos cerrados en términos de conjuntos abiertos.
Se dice que un conjunto\(A \subseteq(S, \rho)\) está cerrado si su complemento\(-A=S-A\) está abierto, es decir, solo tiene puntos interiores.
Es decir, cada uno\(p \in-A\) (afuera\(A )\) está en algún globo\(G_{p} \subseteq-A\) para que
\[A \cap G_{p}=\emptyset.\]
(Continuación).
(5) Los conjuntos\(\emptyset\) y\(S\) están cerrados, por sus complementos,\(S\) y\(\emptyset,\) son abiertos, como se señaló anteriormente. Así, un conjunto puede ser tanto cerrado como abierto (“clopen”).
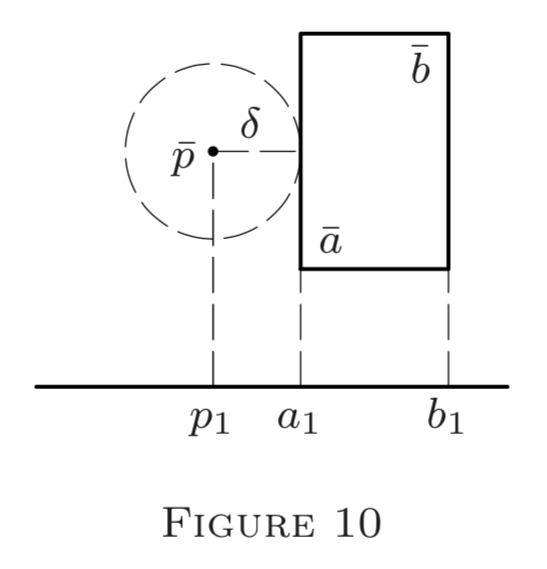
(6) Todos los globos cerrados dentro\((S, \rho)\) y todos los intervalos cerrados en\(E^{n}\) son conjuntos cerrados por Definición\(3 .\) Indeed (ver Figuras 9 y\(10 ),\) si\(A=\overline{G}_{q}(r)\) o\(A=[\overline{a}, \overline{b}]\), entonces cualquier punto\(p\) exterior\(A\) puede ser encerrado en un globo\(G_{p}(\delta)\) disjunta de\(A ;\) así, por \(3, A\)La definición es cerrada (ver Problema 12\()\).
(7) Un conjunto de un punto\(\{q\}\) (también llamado “singleton”) en siempre\((S, \rho)\) está cerrado, porque cualquier\(p\) exterior\(\{q\}(p \neq q)\) está en un globo\(\{q\}\) disgregado de por Teorema 1 En un espacio discreto (§§11,) Ejemplo (3)), también\(\{q\}\) está abierto ya que es un\(g\) lóbulo abierto,\(\{q\}=G_{q}\left(\frac{1}{2}\right)(\) ¿por qué? \() ;\)entonces es “clopen". De ahí que en ese espacio, todos los conjuntos sean “clopen”. Para\(p \in A\) implica de\(\{p\}=G_{p}\left(\frac{1}{2}\right) \subseteq A ;\) manera similar para\(-A .\) Así\(A\) y\(-A\) tener puntos interiores solamente, por lo que ambos están abiertos.
(8) El intervalo\((a, b]\) en no\(E^{1}\) es abierto ni cerrado. (¿Por qué?)
III. (El resto de esta sección podrá ser diferido hasta el Capítulo (4, §10.)
La unión de cualquier familia finita o infinita de conjuntos abiertos\(A_{i}(i \in I)\), denotada
\[\bigcup_{i \in I} A_{i},\]
está abierto en sí mismo. Así también es
\[\bigcap_{i=1}^{n} A_{i}\]
para finitamente muchos juegos abiertos. (Esto falla para infinitamente muchos conjuntos\(A_{i} ;\) ver Problema 11 a continuación.)
- Prueba
-
Debemos demostrar que cualquier punto\(p\) de\(A=\bigcup_{i} A_{i}\) es interior a\(A\).
Ahora bien si\(p \in \bigcup_{i} A_{i}, p\) está en algunos\(A_{i},\) y es un punto interior de\(A_{i}\) (para\(A_{i}\) está abierto, por suposición). Así hay un globo
\[G_{p} \subseteq A_{i} \subseteq A,\]
según se requiera.
Para las intersecciones finitas, basta con considerar dos conjuntos abiertos\(A\) y\(B\) (para\(n\) conjuntos, todo luego sigue por inducción). Debemos demostrar que cada uno\(p \in A \cap B\) es interior para\(A \cap B .\)
Ahora como\(p \in A\) y\(A\) está abierto, tenemos algunos\(G_{p}\left(\delta^{\prime}\right) \subseteq A .\) De igual manera, hay\(G_{p}\left(\delta^{\prime \prime}\right) \subseteq B .\) Entonces el más pequeño de los dos globos, llamarlo\(G_{p},\) está en ambos\(A\) y\(B,\) así
\[G_{p} \subseteq A \cap B\]
y\(p\) es interior de\(A \cap B,\) hecho. \(\square\)
Si los conjuntos\(A_{i}(i \in I)\) están cerrados, también lo es
\[\bigcap_{i \in I} A_{i}\]
(incluso para infinitamente muchos conjuntos). Así también es
\[\bigcup_{i=1}^{n} A_{i}\]
para finitamente muchos conjuntos cerrados\(A_{i} .\) (Una vez más, esto falla para infinitamente muchos conjuntos\(A_{i} . )\)
- Prueba
-
Vamos\(A=\bigcap_{i \in I} A_{i} .\) Para probar que\(A\) está cerrado, demostramos que\(-A\) está abierto.
Ahora por teoría de conjuntos (ver Capítulo 1, §§1-3, Teorema 2),
\[-A=-\bigcap_{i} A_{i}=\bigcup_{i}\left(-A_{i}\right),\]
donde los\(\left(-A_{i}\right)\) están abiertos (para los\(A_{i}\) están cerrados\() .\) Así por Teorema\(2,-A\) está abierto, según se requiera.
La segunda aserción (como\(\bigcup_{i=1}^{n} A_{i} )\) sigue de manera bastante similar. \(\square\)
\(A\)conjunto no vacío\(A \subseteq(S, \rho)\) está abierto iff\(A\) es una unión de globos abiertos.
Porque si\(A\) es tal unión, está abierta por Teorema\(2 .\) Por el contrario, si\(A\) está abierto, entonces cada uno\(p \in A\) está en algunos\(G_{p} \subseteq A .\) Todos esos\(G_{p}(p \in A)\) cubren todos\(A,\) así\(A \subseteq \bigcup_{p \in A} G_{p} .\) también,\(\bigcup_{p \in A} G_{p} \subseteq A\) ya que todos\(G_{p}\) están en\(A .\) Así
\[A=\bigcup_{p \in A} G_{p}.\]
Cada conjunto finito\(F\) en un espacio métrico\((S, \rho)\) está cerrado.
- Prueba
-
Si\(F=\emptyset, F\) está cerrado por Ejemplo\((5) .\) Si\(F \neq \emptyset,\) vamos
\[F=\left\{p_{1}, \ldots, p_{n}\right\}=\bigcup_{k=1}^{n}\left\{p_{k}\right\}.\]
Ahora por Ejemplo\((7),\) cada uno\(\left\{p_{k}\right\}\) está cerrado; de ahí que así sea\(F\) por teorema\(3 . \square\)
Nota. La familia de todos los conjuntos abiertos en un espacio dado\((S, \rho)\) se denota por\(\mathcal{G}\); la de todos los conjuntos cerrados, por\(\mathcal{F} .\) Así\(" A \in \mathcal{G}^{\prime \prime}\) significa que\(A\) está abierto; “Un\(\in \mathcal{F}^{\prime \prime}\) medio que\(A\) está cerrado. Por Teoremas 2 y\(3,\) tenemos
\[(\forall A, B \in \mathcal{G}) \quad A \cup B \in \mathcal{G} \text{ and } A \cap B \in \mathcal{G};\]
similar para\(\mathcal{F} .\) Esta es una especie de “ley de cierre”. Eso decimos\(\mathcal{F}\) y\(\mathcal{G}\) estamos “cerrados bajo uniones e intersecciones finitas”.
En conclusión, consideremos cualquier subespacio\((A, \rho)\) de\((S, \rho) .\) Como sabemos a partir del §11 es un espacio métrico en sí mismo, por lo que tiene sus propios conjuntos abiertos y cerrados (los cuales deben consistir en puntos de\(A\) solamente\() .\) Mostraremos ahora que se obtienen de los de\((S, \rho)\) al intersectar estos últimos conjuntos con\(A .\)
Dejar\((A, \rho)\) ser un subespacio de\((S, \rho) .\) Entonces los conjuntos abiertos (cerrados) en\((A, \rho)\) son exactamente todos los conjuntos de la forma\(A \cap U,\) con\(U\) abierto\((\) cerrado\()\) en\(S\).
- Prueba
-
Let\(G\) be open in\((A, \rho) .\) Por Corolario\(1, G\) es la unión de algunos globos abiertos\(G_{i}^{*}(i \in I)\) en\((A, \rho) .\) (Por brevedad, omitimos los centros y radios; también omitimos el caso trivial\(G=\emptyset .\)
\[G=\bigcup_{i} G_{i}^{*}=\bigcup_{i}\left(A \cap G_{i}\right)=A \cap \bigcup_{i} G_{i},\]
por teoría de conjuntos (ver Capítulo 1, §§1-3,\) Problema 9).
De nuevo por Corolario\(1, U=\bigcup_{i} G_{i}\) es un conjunto abierto en\((S, \rho) .\) Así\(G\) tiene la forma
\[A \cap \bigcup_{i} G_{i}=A \cap U,\]
con\(U\) abierto en\(S,\) como se afirma.
Por el contrario, supongamos lo último,\(p \in A\) y vamos\(p \in G .\) Entonces y\(p \in U .\) Como\(U\) está abierto adentro\((S, \rho),\) hay un globo\(G_{p}\) en\((S, \rho)\) tal que\(p \in G_{p} \subseteq U .\) Como\(p \in A,\) tenemos
\[p \in A \cap G_{p} \subseteq A \cap U.\]
Sin embargo,\(A \cap G_{p}\) es un globo en\((A, \rho),\) llamarlo\(G_{p}^{*} .\) Así
\[p \in G_{p}^{*} \subseteq A \cap U=G;\]
es decir,\(p\) es un punto interior de\(G\) en\((A, \rho) .\) Vemos que cada uno\(p \in G\) es interior a\(G,\) como un conjunto en\((A, \rho),\) así\(G\) está abierto en\((A, \rho) .\)
Esto prueba el teorema de los sets abiertos. Ahora\(F\) déjese cerrar en\((A, \rho) .\) Entonces por Definición\(3, A-F\) está abierto en\((A, \rho) .\) (Por supuesto, al trabajar en\((A, \rho)\), reemplazamos\(S\) por\(A\) en tomar complementos.) Déjalo\(G=A-F,\) así\(F=A-G,\) y\(G\) está abierto en\((A, \rho) .\) Por lo que se mostró arriba,\(G=A \cap U\) con\(U\) open in\(S\).
Así
\[F=A-G=A-(A \cap U)=A-U=A \cap(-U)\]
por teoría de conjuntos. Aquí\(-U=S-U\) está cerrado\((S, \rho)\) ya que\(U\) está abierto ahí. Así\(F=A \cap(-U),\) como se requiera.
La prueba de lo contrario (para sets cerrados) se deja como ejercicio. \(\square\)


