3.9: Conjuntos acotados. Diámetros
- Page ID
- 113840
I. Geométricamente, el diámetro de un globo cerrado\(E^{n}\) podría definirse como la distancia máxima entre dos de sus puntos. En un globo abierto en no\(E^{n},\) hay distancia “máxima” (¿por qué?) , pero aún podemos considerar la suprema de todas las distancias dentro del globo. Además, esto tiene sentido en cualquier conjunto\(A \subseteq(S, \rho) .\) Así lo aceptamos como una definición general, para cualquier conjunto de este tipo.
El diámetro de un conjunto\(A \neq \emptyset\) en un espacio métrico\((S, \rho),\) denotado\(d A,\) es el supremo (in\(E^{*}\)) de todas las distancias\(\rho(x, y),\) con\(x, y \in A ;^{1}\) símbolos,
\[d A=\sup _{x, y \in A} \rho(x, y).\]
Si\(A=\emptyset,\) ponemos\(d A=0 .\) Si\(d A<+\infty, A\) se dice que está acotado\((\) en\((S, \rho) ) .\)
Equivalentemente, podríamos definir un conjunto acotado como en el enunciado del siguiente teorema.
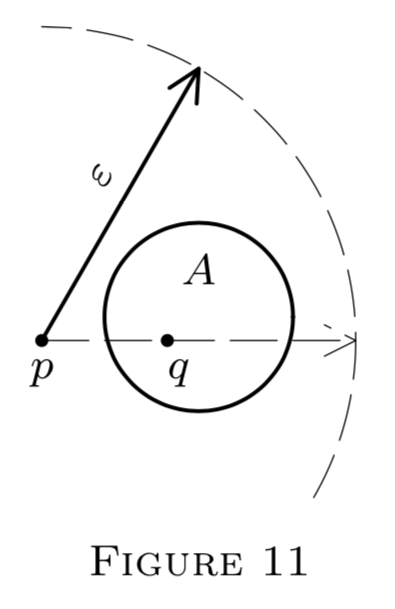
\(A\)conjunto\(A \subseteq(S, \rho)\) está limitado iff\(A\) está contenido en algún globo. Si es así, el centro p de este globo se puede elegir a voluntad.
- Prueba
-
Si\(A=\emptyset,\) todo es trivial.
Así vamos\(A \neq \emptyset ;\) a dejar\(q \in A,\) y elegir cualquier\(p \in S .\) Ahora si\(A\) está acotado, entonces\(d A<+\infty,\) así podemos elegir un real\(\varepsilon>\)\(\rho(p, q)+d A\) como un radio adecuado para un globo\(G_{p}(\varepsilon) \supseteq A(\) ver Figura 11 para la motivación\().\) Ahora bien, si\(x \in A,\) entonces por la definición de\(d A\) \(\rho(q, x) \leq d A ;\)así por la ley del triángulo,
\(\begin{aligned} \rho(p, x) & \leq \rho(p, q)+\rho(q, x) \\ & \leq \rho(p, q)+d A<\varepsilon; \end{aligned}\)
es decir,\(x \in G_{p}(\varepsilon) .\) así\((\forall x \in A) x \in G_{p}(\varepsilon)\) como se requiera.
Por el contrario, si\(A \subseteq G_{p}(\varepsilon),\) entonces alguno también\(x, y \in A\) están en\(G_{p}(\varepsilon) ;\) tal\(\rho(x, p)<\varepsilon\) y de\(\rho(p, y)<\varepsilon,\) dónde
\[\rho(x, y) \leq \rho(x, p)+\rho(p, y)<\varepsilon+\varepsilon=2 \varepsilon.\]
Así 2\(\varepsilon\) es un límite superior de todos\(\rho(x, y)\) con\(x, y \in A .\) Por lo tanto,
\[d A=\sup \rho(x, y) \leq 2 \varepsilon<+\infty;\]
es decir,\(A\) está acotado, y todo está probado. \(\square\)
Como caso especial obtenemos lo siguiente.
\(A\)conjunto\(A \subseteq E^{n}\) está acotado iff hay un real\(K>0\) tal que
\[(\forall \overline{x} \in A) \quad|\overline{x}|<K\]
(*de manera similar en\(C^{n}\) y otros espacios normados).
- Prueba
-
Por teorema\(1(\) elegir\(\overline{0}\) para\(p), A\) está limitado iff\(A\) está contenido en algún globo\(G_{\overline{0}}(\varepsilon)\) sobre\(\overline{0} .\) Eso es,
\[(\forall \overline{x} \in A) \quad \overline{x} \in G_{\overline{0}}(\varepsilon)\text{ or } \rho(\overline{x}, \overline{0})=|\overline{x}|<\varepsilon.\]
Así\(\varepsilon\) es lo requerido\(K\). (*La prueba para espacios normados es la misma.) \(\square\)
Nota 1. En\(E^{1},\) esto significa que
\[(\forall x \in A) \quad-K<x<K;\]
es decir,\(A\) está delimitado por\(-K\) y\(K .\) Esto concuerda con nuestra definición anterior, dada en el Capítulo 2, §8-9.
Precaución: Los límites superior e inferior no están definidos\((S, \rho),\) en general.
(1)\(\emptyset\) está acotado, con\(d \emptyset=0,\) por definición.
(2) Dejar\(A=[\overline{a}, \overline{b}]\) entrar\(E^{n},\) con\(d=\rho(\overline{a}, \overline{b})\) su diagonal. Por Corolario 1 en §7\(d\) es la distancia más grande\(A .\) en En intervalos no cerrados, todavía tenemos
\[d=\sup _{x, y \in A} \rho(x, y)=d A<+\infty\text{ (see Problem 10 (ii)).}\]
Por lo tanto, todos los intervalos en\(E^{n}\) están delimitados.
(3) Cada globo\(G_{p}(\varepsilon)\) en\((S, \rho)\) está acotado, con\(d G_{p}(\varepsilon) \leq 2 \varepsilon<+\infty,\) como se mostró en la prueba del Teorema\(1 .\) Véase, sin embargo, Problemas 5 y 6 a continuación.
(4) Todo no\(E^{n}\) está acotado, bajo la métrica estándar, porque si\(E^{n}\) tuviera un diámetro finito\(d,\) ninguna distancia en\(E^{n}\) superaría\(d ;\) sino\(\rho\left(-d \overline{e}_{1}, d \overline{e}_{1}\right)=2 d\), ¡una contradicción!
(5) Por otro lado, bajo la métrica discreta §11, Ejemplo (3)), cualquier conjunto (incluso todo el espacio) está contenido en\(G_{p}(3)\) y por lo tanto acotado. Lo mismo se aplica a la métrica\(\rho^{\prime}\) definida para\(E^{*}\) en el Problema 5 de §§11, ya que las distancias por debajo de esa métrica nunca superan\(2,\) y así\(E^{*} \subseteq G_{p}(3)\) para cualquier elección de\(p\).
Nota 2. Esto muestra que la delimitación depende de la métrica\(\rho .\) Un conjunto puede estar limitado bajo una métrica y no delimitado bajo otra. Se dice que una métrica\(\rho\) está limitada si todos los conjuntos están delimitados bajo\(\rho\) (como en el Ejemplo (5)).
El problema 9 del §11 muestra que cualquier métrica\(\rho\) puede transformarse en una acotada, incluso conservando todos los globos suficientemente pequeños; en la parte (i) del problema, incluso los radios siguen siendo los mismos si lo son\(\leq 1\).
Nota 3. A menudo se usa una idea similar a la del diámetro para definir distancias entre conjuntos. Si\(A \neq \emptyset\) y\(B \neq \emptyset\) en\((S, \rho),\) definimos\(\rho(A, B)\) ser el infimum de todas las distancias\(\rho(x, y),\) con\(x \in A\) y\(y \in B .\) En particular, si\(B=\{p\}\) (un singleton\(),\) escribimos\(\rho(A, p)\) para\(\rho(A, B).\) Así
\[\rho(A, p)=\inf _{x \in A} \rho(x, p).\]
II. La definición de amplitud se extiende, de manera natural, a secuencias y funciones. Escribimos brevemente\(\left\{x_{m}\right\} \subseteq(S, \rho)\) para una secuencia de puntos en\((S, \rho)\), y\(f : A \rightarrow(S, \rho)\) para un mapeo de un conjunto arbitrario\(A\) en el espacio\(S .\) En lugar de “secuencia infinita con término general\(x_{m},\)" decimos “la secuencia”\(x_{m}\).
\(\left\{x_{m}\right\} \subseteq(S, \rho)\)Se dice que una secuencia está limitada si su rango está limitado,\((S, \rho),\) es decir, si todos sus términos\(x_{m}\) están contenidos en algún globo en\((S, \rho).\)
En\(E^{n},\) este medio (por Teorema 2\()\) que
\[(\forall m) \quad\left|x_{m}\right|<K\]
para algunos fijos\(K \in E^{1}.\)
\(f : A \rightarrow(S, \rho)\)Se dice que una función está limitada en un conjunto si el conjunto\(B \subseteq A\) de imágenes\(f[B]\) está limitado, es\((S, \rho) ;\) decir, iff todos los valores de función\(f(x),\) con\(x \in B,\) están en algún globo en\((S, \rho)\).
En\(E^{n},\) esto significa que
\[(\forall x \in B) \quad|f(x)|<K\]
para algunos fijos\(K \in E^{1}.\)
Si simplemente\(B=A,\) decimos que\(f\) está acotado.
Nota 4. Si\(S=E^{1}\) o\(S=E^{*},\) podemos hablar también de límites superiores e inferiores. Es costumbre llamar al sup\(f[B]\) también el supremum de\(f\) on\(B\) y denotarlo por símbolos como
\[\sup _{x \in B} f(x)\text{ or } \sup \{f(x) | x \in B\}.\]
En el caso de las secuencias, a menudo escribimos sup\(_{m} x_{m}\) o\(x_{m}\) sup; de manera similar para infima, maxima y minima.
a) La secuencia
\[x_{m}=\frac{1}{m} \quad\text{ in } E^{1}\]
está acotado ya que todos los términos\(x_{m}\) están en el intervalo\((0,2)=G_{1}(1) .\) Tenemos inf\(x_{m}=0\) y\(\sup x_{m}=\max x_{m}=1.\)
b) La secuencia
\[x_{m}=m \quad\text{ in } E^{1}\]
está delimitado por debajo (por 1\()\) pero no arriba. Tenemos inf\(x_{m}=\min x_{m}=1\) y\(\sup x_{m}=+\infty\) (en\(E^{*})\).
(c) Definir\(f : E^{1} \rightarrow E^{1}\) por
\[f(x)=2 x.\]
Este mapa está delimitado en cada intervalo finito\(B=(a, b)\) ya que\(f[B]=\)\((2 a, 2 b)\) es en sí mismo un intervalo y por lo tanto delimitado. Sin embargo, no\(f\) está acotado en todos\(E^{1}\) ya que no\(f\left[E^{1}\right]=E^{1}\) es un conjunto acotado.
d) Bajo una métrica acotada\(\rho,\) todas las funciones\(f : A \rightarrow(S, \rho)\) están delimitadas.
e) El llamado mapa de identidad\(S, f : S \rightarrow(S, \rho),\) está definido por
\[f(x)=x.\]
Claramente,\(f\) lleva cada conjunto\(B \subseteq S\) sobre sí mismo; es decir,\(f[B]=B .\) Así\(f\) está limitado en\(B\) iff\(B\) es en sí mismo un conjunto acotado en\((S, \rho).\)
(f) Definir\(f : E^{1} \rightarrow E^{1}\) por
\[f(x)=\sin x.\]
Entonces\(f\left[E^{1}\right]=[-1,1]\) es un conjunto acotado en el espacio de rango\(E^{1} .\) Así\(f\) es acotado en\(E^{1}\) (brevemente, acotado).


