4.9: La propiedad de valor intermedio
- Page ID
- 113917
This page is a draft and is under active development.
\( f : A \rightarrow E ^ { * } \)Se dice que una función tiene la propiedad de valor intermedio, o propiedad Darboux,\( ^ { 1 } \) en un conjunto\( B \subseteq A \) iff, junto con dos valores de función cualesquiera\( f ( p ) \) y también\( f \left( p _ { 1 } \right) \left( p , p _ { 1 } \in B \right) , \) toma todos los valores intermedios entre\( f ( p ) \) y\( f \left( p _ { 1 } \right) \) en algunos puntos de\( B \) .
En otras palabras, el conjunto de imágenes\( f [ B ] \) contiene todo el intervalo entre\( f ( p ) \) y\( f \left( p _ { 1 } \right) \) en\( E ^ { * } . \)
Nota 1. De ello se deduce que en\( f [ B ] \) sí mismo es un intervalo finito o infinito en\( E ^ { * } , \) con puntos finales inf\( f [ B ] \) y\( \sup f [ B ] . \) (¡Verify!)
Geométricamente, si\( A \subseteq E ^ { 1 } , \) esto significa que la curva\( y = f ( x ) \) cumple con todas las líneas horizontales\( y = q , \)\( f \left( p _ { 1 } \right) . \) para\( q \) entre\( f ( p ) \) y Por ejemplo, en la Figura 13 en\( § 1 , \) tenemos una curva “suave” que corta cada línea horizontal\( y = q \) entre\( f ( 0 ) \) y\( f \left( p _ { 1 } \right) ; \) así \( f \)tiene la propiedad Darboux en\( \left[ 0 , p _ { 1 } \right] . \) En las Figuras 14 y\( 15 , \) hay una “brecha” en\( p \); el inmueble falla. En Ejemplo (f) de\( § 1 , \) la propiedad se sostiene sobre todos\( E ^ { 1 } \) a pesar de una discontinuidad en\( 0 . \) Así no implica continuidad.
Intuitivamente, parece plausible que una “curva continua” deba cortar todas las horizontales intermedias. Una prueba precisa de funciones continuas en un intervalo, fue dada independientemente por Bolzano y Weierstrass (lo mismo que en el Teorema 2 del Capítulo 3, §16). A continuación damos una versión más general de la prueba de Bolzano basada en la noción de conjunto convexo y conceptos relacionados.
Un conjunto\( B \) en\( E ^ { n }\) (* o en otro espacio normado) se dice que es convexo iff para cada segmento\( \overline { a } , \overline { b } \in B \) de línea\( L [ \overline { a } , \overline { b } ] \) es un subconjunto de\( B \).
Una unión poligonal\( \overline { a } \) y\( \overline { b } \) es cualquier unión finita de segmentos de línea (una “línea discontinua”) de la forma
\ [
\ bigcup _ {i = 0} ^ {m - 1} L\ izquierda [\ overline {p} _ {i},\ overline {p} _ {i + 1}\ derecha]\ texto {con}\ overline {p} _ _ {0} =\ overline {a}\ text {y}\ overline {p} _ _ {m} =\ overline {b}.
\]
\( B \)Se dice que el conjunto está conectado a un polígono (o convexo por partes) si dos puntos\( \overline { a } , \overline { b } \in B \) pueden unirse mediante un polígono contenido en\( B \).
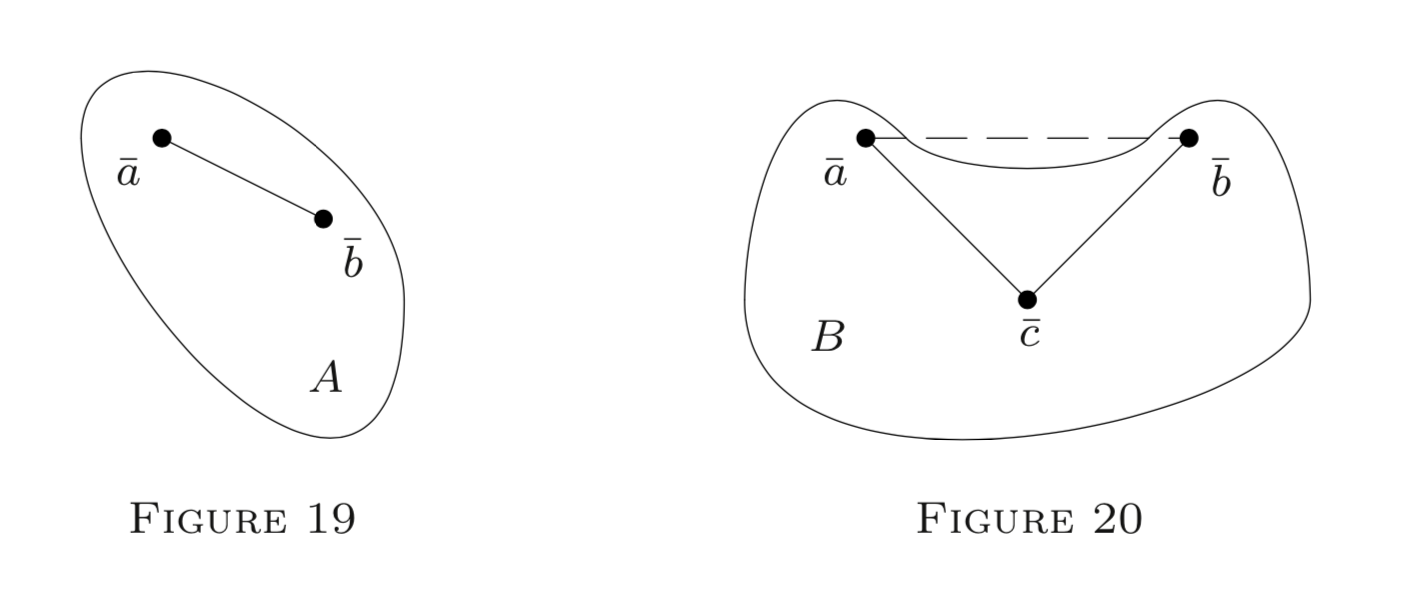
Cualquier globo en\(E^{n}\) (* o en otro espacio normado) es convexo, por lo que también lo es cualquier intervalo dentro\(E^{n}\) o dentro\(E^{*}\). Las figuras 19 y 20 representan un conjunto convexo\(A\) y un conjunto\(B\) conectado a polígonos no\(E^{2}\) es convexo; tiene una “cavidad”).
Necesitaremos un lema sencillo que también sea digno de mención por derecho propio.
Cada secuencia de contracciones de segmentos de línea cerrada\(L\left[\overline{p}_{m}, \overline{q}_{m}\right]\) en\(E^{n}\) (* o en cualquier otro espacio normado) tiene una intersección no voide; es decir, hay un punto
\[\overline{p} \in \bigcap_{m=1}^{\infty} L[\overline{p}_{m}, \overline{q}_{m}].\]
- Prueba
-
Utilice el teorema de Cantor (Teorema 5 de §6) y el Ejemplo (1) en §8. \(\square\)
Ya estamos listos para el teorema de Bolzano. La prueba a utilizar es típica de las llamadas “pruebas de bisección”. (Véase también §6, Problemas 9 y 10 para tales pruebas.)
Si\(f : B \rightarrow E^{1}\) es relativamente continuo en un conjunto conectado a polígonos\(B\) en\(E^{n}\) (* o en otro espacio normado), entonces\(f\) tiene la propiedad Darboux en\(B .\)
En particular, si\(B\) es convexo y si\(f(\overline{p})<c<f(\overline{q})\) para algunos\(\overline{p}, \overline{q} \in B,\) entonces hay un punto\(\overline{r} \in L(\overline{p}, \overline{q})\) tal que\(f(\overline{r})=c\).
- Prueba
-
Primero, deja que\(B\) sea convexo. Buscando una contradicción, supongamos\(\overline{p}, \overline{q} \in B\) con
\[f(\overline{p})<c<f(\overline{q}),\]
sin embargo\(f(\overline{x}) \neq c\) para todos\(\overline{x} \in L(\overline{p}, \overline{q})\).
\(P\)Sea el conjunto de todos aquellos\(\overline{x} \in L[\overline{p}, \overline{q}]\) para los que\(f(\overline{x})<c,\) i.e.,
\[P=\{\overline{x} \in L[\overline{p}, \overline{q}] | f(\overline{x})<c\},\]
y dejar
\[Q=\{\overline{x} \in L[\overline{p}, \overline{q}] | f(\overline{x})>c\}.\]
Entonces\(\overline{p} \in P, \overline{q} \in Q, P \cap Q=\emptyset,\) y\(P \cup Q=L[\overline{p}, \overline{q}] \subseteq B\). (¿Por qué?)
Ahora vamos
\[\overline{r}_{0}=\frac{1}{2}(\overline{p}+\overline{q})\]
ser el punto medio en\(L[\overline{p}, \overline{q}].\) Claramente,\(\overline{r}_{0}\) está en\(P\) o en\(Q.\) Así se\(L[\overline{p}, \overline{q}]\) divide en dos subsegmentos, uno de los cuales debe tener su punto final izquierdo adentro\(P\) y su extremo derecho en\(Q.\)
Denotamos este segmento cerrado en particular por Entonces\(L\left[\overline{p}_{1}, \overline{q}_{1}\right], \overline{p}_{1} \in P, \overline{q}_{1} \in Q.\) tenemos
\[L[\overline{p}_{1}, \overline{q}_{1}] \subseteq L[\overline{p}, \overline{q}] \text { and }|p_{1}-q_{1}|=\frac{1}{2}|\overline{p}-\overline{q}|. \text { (Verify!) }\]
Ahora biseccionamos\(L[\overline{p}_{1}, \overline{q}_{1}]\) y repetimos el proceso. Así vamos
\[\overline{r}_{1}=\frac{1}{2}(\overline{p}_{1}+\overline{q}_{1}).\]
Por el mismo argumento, obtenemos un subsegmento cerrado\(L\left[\overline{p}_{2}, \overline{q}_{2}\right] \subseteq L\left[\overline{p}_{1}, \overline{q}_{1}\right]\) con\(\overline{p}_{2} \in P, \overline{q}_{2} \in Q,\) y
\[\left|\overline{p}_{2}-\overline{q}_{2}\right|=\frac{1}{2}\left|\overline{p}_{1}-\overline{q}_{1}\right|=\frac{1}{4}|\overline{p}-\overline{q}|.\]
A continuación, biseccionamos\(L\left[\overline{p}_{2}, \overline{q}_{2}\right],\) y así sucesivamente. Continuando este proceso indefinidamente, obtenemos una secuencia infinita de contracciones de segmentos de línea cerrada\(L\left[\overline{p}_{m}, \overline{q}_{m}\right]\) tal que
\[(\forall m) \quad \overline{p}_{m} \in P, \overline{q}_{m} \in Q,\]
y
\[\left|\overline{p}_{m}-\overline{q}_{m}\right|=\frac{1}{2^{m}}|\overline{p}-\overline{q}| \rightarrow 0 \text { as } m \rightarrow+\infty.\]
Por Lemma 1, hay un punto
\[\overline{r} \in \bigcap_{m=1}^{\infty} L\left[\overline{p}_{m}, \overline{q}_{m}\right].\]
Esto implica que
\[(\forall m) \quad\left|\overline{r}-\overline{p}_{m}\right| \leq\left|\overline{p}_{m}-\overline{q}_{m}\right| \rightarrow 0,\]
de donde\(\overline{p}_{m} \rightarrow \overline{r} .\) De igual manera, obtenemos\(\overline{q}_{m} \rightarrow \overline{r}\).
Ahora ya que\(\overline{r} \in L[\overline{p}, \overline{q}] \subseteq B,\) la función\(f\) es relativamente continua en\(\overline{r}\) over\(B\) (por suposición). Por el criterio secuencial, entonces,
\[f\left(\overline{p}_{m}\right) \rightarrow f(\overline{r}) \text { and } f\left(\overline{q}_{m}\right) \rightarrow f(\overline{r}).\]
Por otra parte,\(f\left(\overline{p}_{m}\right)<c<f\left(\overline{q}_{m}\right)\left(\text { for } \overline{p}_{m} \in P \text { and } \overline{q}_{m} \in Q\right) .\)\(m \rightarrow+\infty,\) Dejando pasar a límites (Capítulo 3, §15, Corolario 1) y obtener
\[f(\overline{r}) \leq c \leq f(\overline{r}),\]
así que eso no\(\overline{r}\) es\(P\) ni en el\(Q,\) que hay una contradicción. Esto completa la prueba para una convexa\(B\).
La extensión a conjuntos conectados a polígonos se deja como un ejercicio (ver Problema 2 a continuación). Así todo está probado. \(\square\)
Nota 2. En particular, el teorema se aplica si\(B\) es un globo o un intervalo.
Así, la continuidad en un intervalo implica la propiedad Darboux. El inverso falla, como hemos señalado. Sin embargo, para funciones monótonas, obtenemos el siguiente teorema.
Si una función\(f : A \rightarrow E^{1}\) es monótona y tiene la propiedad Darboux en un intervalo finito o infinito\((a, b) \subseteq A \subseteq E^{1},\), entonces es continua en\((a, b).\)
- Prueba
-
Buscando una contradicción, supongamos que\(f\) es discontinuo en algunos\(p \in(a, b)\).
Para la definición,\(f \uparrow\) vamos\((a, b) .\) Entonces por los Teoremas 2 y 3 en §5, tenemos uno\(f\left(p^{-}\right)<f(p)\)\(f(p)<f\left(p^{+}\right)\) o ambos, sin valores de función en el medio.
Por otro lado, ya que\(f\) tiene la propiedad Darboux, los valores de la función\(f(x)\) para\(x\) en\((a, b)\) llenar un intervalo completo (ver Nota 1). Por lo tanto, es imposible\(f(p)\) que sea el único valor de función entre\(f\left(p^{-}\right)\) y\(f\left(p^{+}\right)\) a menos que\(f\) sea constante cerca\(p,\) pero entonces también es continuo en el\(p,\) que excluimos. Esta contradicción completa la prueba. \(\square\)
Nota 3. El teorema también se mantiene (con una prueba similar) para intervalos no abiertos, pero la continuidad en los puntos finales es relativa (derecha a\(a,\) izquierda en\(b).\)
Si\(f : A \rightarrow E^{1}\) es estrictamente monótona y continua cuando se restringe a un intervalo finito o infinito\(B \subseteq A \subseteq E^{1},\) entonces su inverso\(f^{-1}\) tiene las mismas propiedades en el conjunto\(f[B]\) (en sí mismo un intervalo, por la Nota 1 y Teorema 1).
- Prueba
-
Es fácil ver que\(f^{-1}\) está aumentando (disminuyendo) si\(f\) es; la prueba se deja como ejercicio. Así\(f^{-1}\) es monótona encendido\(f[B]\) si\(f\) es así sucesivamente\(B\). Para probar la continuidad relativa de\(f^{-1},\) utilizamos el Teorema 2, es decir, mostrar que\(f^{-1}\) tiene la propiedad Darboux en\(f[B].\)
Así vamos\(f^{-1}(p)<c<f^{-1}(q)\) para algunos\(p, q \in f[B] .\) Buscamos un\(r \in f[B]\) tal que\(f^{-1}(r)=c,\) es decir,\(r=f(c) .\) Ahora ya que\(p, q \in f[B],\) los números\(f^{-1}(p)\) y\(f^{-1}(q)\) están en\(B,\) un intervalo. De ahí que también el valor intermedio\(c\) esté en\(B\); así pertenece al dominio de\(f,\) y así\(f(c)\) existe el valor de la función. Por lo tanto, basta con poner\(r=f(c)\) para obtener el resultado. \(\square\)
a) Definir\(f : E^{1} \rightarrow E^{1}\) por
\[f(x)=x^{n} \text { for a fixed } n \in N.\]
Como\(f\) es continuo (siendo un monomio), tiene la propiedad Darboux en la\(1,\) configuración\(E^{1} .\) By Note que\(B=[0,+\infty),\) tenemos\(f[B]=[0,+\infty)\). (¿Por qué?) Además,\(f\) está aumentando estrictamente en\(B\). Así, por el Teorema 3, la función inversa\(f^{-1}\) (es decir, la enésima función raíz) existe y es continua en\(f[B]=[0,+\infty)\).
Si\(n\) es impar, entonces\(f^{-1}\) tiene estas propiedades en todos\(E^{1},\) por una prueba similar; así\(\sqrt[n]{x}\) existe para\(x \in E^{1}\).
b) Funciones logarítmicas. Del ejemplo en §5, recordamos que la función exponencial dada por
\[F(x)=a^{x} \quad(a>0)\]
es continuo y estrictamente monótona en\(E^{1}.\) Su inversa,\(F^{-1},\) se llama la función logarítmica a la base a, denotada logarítmica. Por Teorema 3, es continuo y estrictamente monótona en\(F\left[E^{1}\right].\)
Para arreglar ideas, let\(a>1,\) so\(F \uparrow\) y\(\left(F^{-1}\right) \uparrow.\) By Note 1,\(F\left[E^{1}\right]\) es un intervalo con puntos finales\(p\) y\(r,\) donde
\[p=\inf F\left[E^{1}\right]=\inf \left\{a^{x} |-\infty<x<+\infty\right\}\]
y
\[r=\sup F\left[E^{1}\right]=\sup \left\{a^{x} |-\infty<x<+\infty\right\}.\]
Ahora por el Problema 14 (iii) de §2 (con\(q=0\)),
\[\lim _{x \rightarrow+\infty} a^{x}=+\infty \text { and } \lim _{x \rightarrow-\infty} a^{x}=0.\]
Como\(F \uparrow,\) usamos el Teorema 1 en §5 para obtener
\[r=\sup a^{x}=\lim _{x \rightarrow+\infty} a^{x}=+\infty \text { and } p=\lim _{x \rightarrow-\infty} a^{x}=0.\]
Así\(F\left[E^{1}\right],\) es decir, el dominio de\(\log _{a},\) es el intervalo\((p, r)=(0,+\infty)\). De ello se deduce que\(\log _{a} x\) se define de manera única\((0,+\infty) ;\) porque\(x\) en ella se llama el logaritmo de\(x\) a la base\(a\).
El rango de log\(_{a}\left(\text { i.e. of } F^{-1}\right)\) es el mismo que el dominio de\(F,\) i.e\(E^{1}\).,. Por lo tanto, si\(a>1, \log _{a} x\) aumenta de\(-\infty\) a\(+\infty\) como\(x\) aumenta de 0 a\(+\infty.\) Por lo tanto
\[\lim _{x \rightarrow+\infty} \log _{a} x=+\infty \text { and } \lim _{x \rightarrow 0+} \log _{a} x=-\infty,\]
siempre\(a>1\).
Si se intercambian\(0<a<1,\) los valores de estos límites (ya que\(F \downarrow\) en este caso), pero por lo demás los resultados son los mismos.
Si\(a=e,\) escribimos\(\ln x\) o\(\log x\) para\(\log _{a} x,\) y llamamos\(\ln x\) el logaritmo natural de\(x.\) Su inverso es, por supuesto, el exponencial\(f(x)=e^{x},\) también escrito\(\exp (x).\) Así por definición,\(\ln e^{x}=x\) y
\[x=\exp (\ln x)=e^{\ln x} \quad(0<x<+\infty).\]
(c) La función de potencia\(g :(0,+\infty) \rightarrow E^{1}\) está definida por
\[g(x)=x^{a} \text { for a fixed real } a.\]
Si\(a>0,\) también\(x>0,\) definimos\(g(0)=0.\) Para tenemos
\[x^{a}=\exp \left(\ln x^{a}\right)=\exp (a \cdot \ln x).\]
Así, por las reglas para las funciones compuestas (Teorema 3 y Corolario 2 en §2), la continuidad de\(g\) on se\((0,+\infty)\) desprende de la de las funciones exponenciales y logarítmicas. Si también\(a>0, g\) es continuo en\(0.\) (¡Ejercicio!)


