5.2: Derivadas de Funciones Reales Extendidas
- Page ID
- 114046
Por un tiempo (en §§2 y 3), nos limitamos a funciones reales extendidas. Abajo,\(f\) y\(g\) son reales o reales extendidos (f,\(g : E^{1} \rightarrow E^{*}).\) Suponemos, sin embargo, que no son constantemente infinitos en ningún intervalo\((a, b), a<b\).
Si\(f^{\prime}(p)>0\) en algún\(p \in E^{1},\) entonces
\[x<p<y\]
implica
\[f(x)<f(p)<f(y)\]
para todos\(x, y\) en un globo suficientemente pequeño\(G_{p}(\delta)=(p-\delta, p+\delta).\)
Del mismo modo, si\(f^{\prime}(p)<0,\) entonces\(x<p<y\) implica\(f(x)>f(p)>f(y)\) para\(x, y\) en algunos\(G_{p}(\delta).\)
- Prueba
-
Si\(f^{\prime}(p)>0,\) se excluye el caso “0" en la Definición 1 de §1, así
\[f^{\prime}(p)=\lim _{x \rightarrow p} \frac{\Delta f}{\Delta x}>0.\]
De ahí que también debemos tener\(\Delta f / \Delta x>0\) para\(x\) en algunos\(G_{p}(\delta)\).
De ello se deduce que\(\Delta f\) y\(\Delta x\) tienen el mismo signo en\(G_{p}(\delta);\) i.e.,
\[f(x)-f(p)>0 \text { if } x>p \text { and } f(x)-f(p)<0 \text { if } x<p.\]
(Esto implica\(f(p) \neq \pm \infty.\) ¿Por qué? De ahí
\[x<p<y \Longrightarrow f(x)<f(p)<f(y),\]
como se reclama; de manera similar en caso\(f^{\prime}(p)<0. \quad \square\)
Si\(f(p)\) es el valor máximo o mínimo de\(f(x)\) for\(x\) en algunos\(G_{p}(\delta),\) entonces\(f^{\prime}(p)=0;\) es decir,\(f\) tiene una derivada cero, o ninguno en absoluto, en\(p.\)
Para, por Lema 1,\(f^{\prime}(p) \neq 0\) excluye un máximo o mínimo en\(p.\) (¿Por qué?)
Nota 1. Por lo tanto,\(f^{\prime}(p)=0\) es una condición necesaria para un máximo o mínimo local en\(p.\) Es insuficiente, sin embargo. Por ejemplo, si no\(f(x)=x^{3}, f\) tiene máximos o mínimos en absoluto, sin embargo\(f^{\prime}(0)=0 .\) Para condiciones suficientes, ver §6.
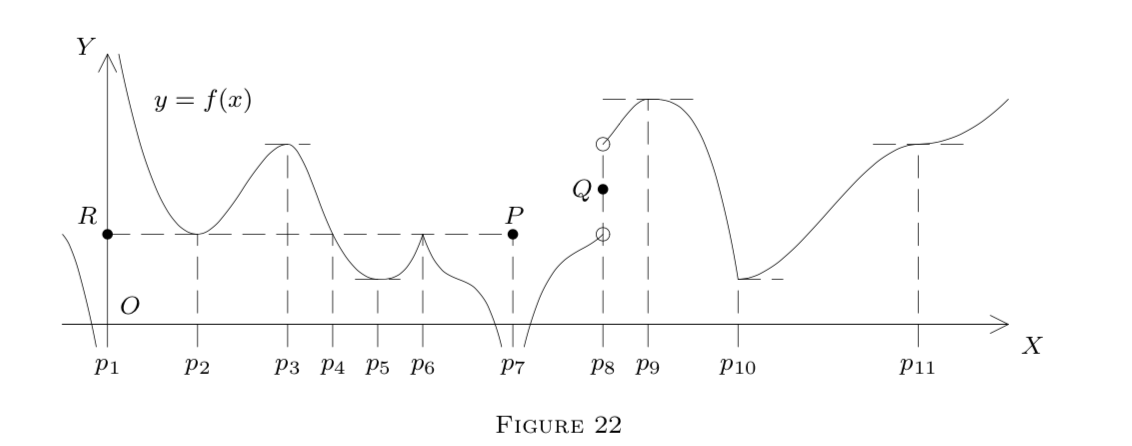
La figura 22 ilustra estos hechos en los puntos\(p_{2}, p_{3}, \ldots, p_{11}.\) Obsérvese que en la figura 22, los puntos aislados\(P, Q, R\) pertenecen a la gráfica.
Geométricamente,\(f^{\prime}(p)=0\) significa que la tangente en\(p\) es horizontal, o que una tangente de dos lados no existe en\(p.\)
Dejar\(f : E^{1} \rightarrow E^{*}\) ser relativamente continuo en un intervalo\([a, b]\), con\(f^{\prime} \neq 0\) on\((a, b).\) Entonces\(f\) es estrictamente monótona encendido\([a, b],\) y\(f^{\prime}\) es signconstant allí (posiblemente 0 en a y b), con\(f^{\prime} \geq 0\) si\(f \uparrow,\) y\(f^{\prime} \leq 0\) si\(f \downarrow\).
- Prueba
-
Por Teorema 2 del Capítulo 4, §8,\(f\) alcanza un menor valor\(m,\) y un valor mayor\(M,\) en algunos puntos de\([a, b].\) Sin embargo, ninguno puede ocurrir en un punto interior porque,\(p \in(a, b),\) por Corolario 1, esto implicaría\(f^{\prime}(p)=0,\) contrario a nuestra suposición.
Así\(M=f(a)\) o\(M=f(b);\) por el momento\(m=f(a).\) asumimos\(M=f(b)\) y debemos tener\(m<M,\) para\(m=M\) haría\(f\) constante en\([a, b]\), implicando\(f^{\prime}=0.\) así\(m=f(a)<f(b)=M.\)
Ahora vamos\(a \leq x<y \leq b\). Aplicando el argumento anterior a cada uno de los intervalos\([a, x],[a, y],[x, y],\) y\([x, b]\) (ahora usando eso\(m=f(a)<f(b)=M )\), encontramos que
\[f(a) \leq f(x)<f(y) \leq f(b). \quad \text { (Why?) }\]
Así\(a \leq x<y \leq b\) implica\(f(x)<f(y);\) es decir,\(f\) aumentos en\([a, b].\) Por lo tanto\(f^{\prime}\) no puede ser negativo en ninguno\(p \in[a, b],\) porque, de lo contrario, por Lema 1,\(f\) disminuiría en\(p.\) Así\(f^{\prime} \geq 0\) en\([a, b].\)
En el caso\(M=f(a)>f(b)=m,\) obtendríamos\(f^{\prime} \leq 0\). \(\quad \square\)
Precaución: La función\(f\) puede aumentar o disminuir\(p\) incluso si\(f^{\prime}(p)=0.\)
Ver Nota 1.
Si:\(E^{1} \rightarrow E^{*}\) es relativamente continuo en\([a, b]\) y si\(f(a)=f(b),\) entonces\(f^{\prime}(p)=0\) para al menos un punto interior\(p \in(a, b)\).
Porque, si\(f^{\prime} \neq 0\) en todo\((a, b),\) entonces por el Teorema 1,\(f\) sería estrictamente monótona en\([a, b],\) lo que la igualdad\(f(a)=f(b)\) sería imposible.
La Figura 22 ilustra esto en los intervalos\(\left[p_{2}, p_{4}\right]\) y\(\left[p_{4}, p_{6}\right],\) con\(f^{\prime}\left(p_{3}\right)=\)\(f^{\prime}\left(p_{5}\right)=0.\) una discontinuidad a 0 provoca un fallo aparente en\([0, p_{2}].\)
Nota 2. El Teorema 1 y el Corolario 2 sostienen aunque\(f(a)\) y\(f(b)\) sean infinitos, si la continuidad se interpreta en el sentido de la métrica\(\rho^{\prime}\) del Problema 5 en el Capítulo 3, §11. (El Teorema 2 de Weierstrass del Capítulo 4, §8 se aplica\(\left(E^{*}, \rho^{\prime}\right),\) con la misma prueba.)
Deje que las funciones\(f, g : E^{1} \rightarrow E^{*}\) sean relativamente continuas y finitas\([a, b]\) y tengan derivadas en\((a, b),\) con\(f^{\prime}\) y\(g^{\prime}\) nunca ambas infinitas en el mismo punto\(p \in(a, b).\) Entonces
\[g^{\prime}(q)[f(b)-f(a)]=f^{\prime}(q)[g(b)-g(a)] \text { for at least one } q \in(a, b).\]
- Prueba
-
Vamos\(A=f(b)-f(a)\) y\(B=g(b)-g(a).\) Debemos demostrarlo\(A g^{\prime}(q)=B f^{\prime}(q)\) para algunos\(q \in(a, b)\). Para ello, considere la función\(h=A g-B f\). Es relativamente continuo y finito\([a, b],\) como son\(g\) y\(f.\) también,
\[h(a)=f(b) g(a)-g(b) f(a)=h(b) . \quad \text { (Verify!) }\]
Así por Corolario 2,\(h^{\prime}(q)=0\) para algunos\(q \in(a, b).\) Aquí, por Teorema 4 de §1,\(h^{\prime}=(A g-B f)^{\prime}=A g^{\prime}-B f^{\prime}.\) (Esto es legítimo, pues, por suposición,\(f^{\prime}\) y\(g^{\prime}\) nunca ambos se vuelven infinitos, por lo que no se producen límites indeterminados.) Así\(h^{\prime}(q)=A g^{\prime}(q)-B f^{\prime}(q)=0,\) y (1) sigue. \(\quad \square\)
Si\(f : E^{1} \rightarrow E^{1}\) es relativamente continuo\([a, b]\) con una derivada en\((a, b),\) entonces
\[f(b)-f(a)=f^{\prime}(q)(b-a) \text { for at least one } q \in(a, b).\]
- Prueba
-
Tomar\(g(x)=x\) en Teorema 2, así\(g^{\prime}=1\) sucesivamente\(E^{1}. \square\)
Nota 3. Geométricamente,
\[\frac{f(b)-f(a)}{b-a}\]
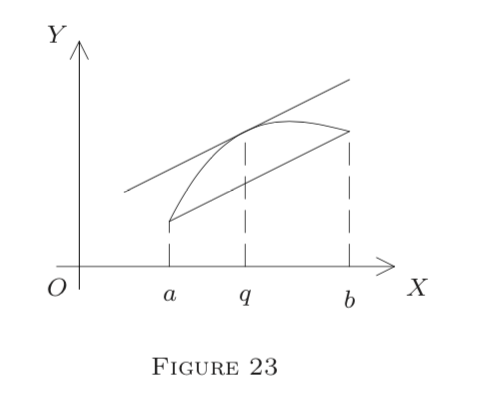
es la pendiente de la secante pasante\((a, f(a))\) y\((b, f(b)),\) y\(f^{\prime}(q)\) es la pendiente de la línea tangente en\(q.\) Así Corolario 3 afirma que la secante es paralela a la tangente en algún punto intermedio\(q;\) ver Figura 23. Teorema 2 establece lo mismo para las curvas dadas paramétricamente:\(x=f(t), y=g(t)\).
Seamos\(f\) como en Corolario 3. Entonces
(i)\(f\) es constante en\([a, b]\) iff\(f^{\prime}=0\) on\((a, b)\);
ii)\(f \uparrow\) en\([a, b]\) iff\(f^{\prime} \geq 0\)\((a, b);\) y
(iii)\(f \downarrow\) en\([a, b]\) iff\(f^{\prime} \leq 0\) on\((a, b)\).
- Prueba
-
Dejar\(f^{\prime}=0\) en\((a, b).\) Si\(a \leq x \leq y \leq b,\) aplicar Corolario 3 al intervalo\([x, y]\) para obtener
\[f(y)-f(x)=f^{\prime}(q)(y-x) \text { for some } q \in(a, b) \text { and } f^{\prime}(q)=0.\]
Así pues\(x, y \in[a, b],\),\(f(y)-f(x)=0\) para así\(f\) es constante.
El resto se deja al lector. \(\quad \square\)
Dejar\(f : E^{1} \rightarrow E^{1}\) ser relativamente continuo y estrictamente monótona en un intervalo\(I \subseteq E^{1}\). Dejar\(f^{\prime}(p) \neq 0\) en algún punto interior\(p \in I.\) Entonces la función inversa\(g=f^{-1}\) (con\(f\) restringido a\(I)\) tiene una derivada en\(q=f(p),\) y
\[g^{\prime}(q)=\frac{1}{f^{\prime}(p)}.\]
(Si\(f^{\prime}(p)=\pm \infty,\) entonces\(g^{\prime}(q)=0.)\)
- Prueba
-
Por Teorema 3 del Capítulo 4, §9,\(g=f^{-1}\) es estrictamente monótona y relativamente continua sobre\(f[I],\) sí mismo un intervalo. Si\(p\) es interior a\(I,\) entonces\(q=f(p)\) es interior a\(f[I].\) (¿Por qué?)
Ahora si\(y \in f[I],\) establecemos
\[\Delta g=g(y)-g(q), \Delta y=y-q, x=f^{-1}(y)=g(y), \text { and } f(x)=y\]
y obtener
\[\frac{\Delta g}{\Delta y}=\frac{g(y)-g(q)}{y-q}=\frac{x-p}{f(x)-f(p)}=\frac{\Delta x}{\Delta f} \text { for } x \neq p.\]
Ahora bien, si\(y \rightarrow q,\) la continuidad de\(g\) a\(q\) rendimientos\(g(y) \rightarrow g(q);\) es decir,\(x \rightarrow p.\) También,\(x \neq p\) iff\(y \neq q\), for\(f\) y\(g\) son funciones uno-a-uno. Por lo tanto podemos sustituir\(y=f(x)\) o\(x=g(y)\) para obtener
\[g^{\prime}(q)=\lim _{y \rightarrow q} \frac{\Delta g}{\Delta y}=\lim _{x \rightarrow p} \frac{\Delta x}{\Delta f}=\frac{1}{\lim _{x \rightarrow p}(\Delta f / \Delta x)}=\frac{1}{f^{\prime}(p)},\]
donde usamos la convención\(\frac{1}{\infty}=0\) si\(f^{\prime}(p)=\infty. \quad \square\)
(A) Dejar
\[f(x)=\log _{a}|x| \text { with } f(0)=0.\]
Vamos\(p>0.\) Entonces\((\forall x>0)\)
\[\begin{aligned} \Delta f &=f(x)-f(p)=\log _{a} x-\log _{a} p=\log _{a}(x / p) \\ &=\log _{a} \frac{p+(x-p)}{p}=\log _{a}\left(1+\frac{\Delta x}{p}\right). \end{aligned}\]
Por lo tanto
\[\frac{\Delta f}{\Delta x}=\log _{a}\left(1+\frac{\Delta x}{p}\right)^{1 / \Delta x}.\]
Ahora vamos\(z=\Delta x / p.\) (¿Por qué es admisible esta sustitución?) Luego usando la fórmula
\[\lim _{z \rightarrow 0}(1+z)^{1 / z}=e \quad \text { (see Chapter 4, §2, Example (C)) }\]
y la continuidad de las funciones log y power, obtenemos
\[f^{\prime}(p)=\lim _{x \rightarrow p} \frac{\Delta f}{\Delta x}=\lim _{z \rightarrow 0} \log _{a}\left[(1+z)^{1 / z}\right]^{1 / p}=\log _{a} e^{1 / p}=\frac{1}{p} \log _{a} e.\]
La misma fórmula resulta también si\(p<0,\) es decir,\(|p|=-p.\) At\(( \pm \infty)\) solo\(p=0, f\) tiene derivados unilaterales (¡verifica!) ,\(f^{\prime}(0)=0\) por lo que por la Definición 1 en §1.
(B) La inversa de la\(_{a}\) función log es la exponencial\(g : E^{1} \rightarrow E^{1},\) con
\[g(y)=a^{y} \quad(a>0, a \neq 1).\]
Por Teorema 3, tenemos
\[\left(\forall q \in E^{1}\right) \quad g^{\prime}(q)=\frac{1}{f^{\prime}(p)}, p=g(q)=a^{q}.\]
Por lo tanto
\[g^{\prime}(q)=\frac{1}{\frac{1}{p} \log _{a} e}=\frac{p}{\log _{a} e}=\frac{a^{q}}{\log _{a} e}.\]
Simbólicamente,
\[\left(\log _{a}|x|\right)^{\prime}=\frac{1}{x} \log _{a} e(x \neq 0) ; \quad\left(a^{x}\right)^{\prime}=\frac{a^{x}}{\log _{a} e}=a^{x} \ln a.\]
En particular, si\(a=e,\) tenemos\(\log _{e} a=1\) y\(\log _{a} x=\ln x ;\) por lo tanto
\[(\ln |x|)^{\prime}=\frac{1}{x}(x \neq 0) \quad \text { and } \quad\left(e^{x}\right)^{\prime}=e^{x} \quad\left(x \in E^{1}\right).\]
(C) La función de potencia\(g :(0,+\infty) \rightarrow E^{1}\) viene dada por
\[g(x)=x^{a}=\exp (a \cdot \ln x) \text { for } x>0 \text { and fixed } a \in E^{1}.\]
Por la regla de la cadena (§1, Teorema 3), obtenemos
\[g^{\prime}(x)=\exp (a \cdot \ln x) \cdot \frac{a}{x}=x^{a} \cdot \frac{a}{x}=a \cdot x^{a-1}.\]
Así tenemos la fórmula simbólica
\[\left(x^{a}\right)^{\prime}=a \cdot x^{a-1} \text { for } x>0 \text { and fixed } a \in E^{1}.\]
Si\(f : E^{1} \rightarrow E^{*}\) es relativamente continuo y tiene una derivada en un intervalo I, entonces\(f^{\prime}\) tiene la propiedad Darboux (Capítulo 4, §9) sobre\(I.\)
- Prueba
-
Dejar\(p, q \in I\) y\(f^{\prime}(p)<c<f^{\prime}(q).\) poner\(g(x)=f(x)-c x.\) Asumir\(g^{\prime} \neq 0\)\((p, q)\) y encontrar una contradicción al Teorema 1. Los detalles se dejan al lector. \(\quad \square\)


