6.7: Funciones inversas e implícitas. Mapas abiertos y cerrados
- Page ID
- 113773
I. “Si\(f \in C D^{1}\) en\(\vec{p},\) ese entonces\(f\) se asemeja a un mapa lineal (es decir,\(d f )\) en\(\vec{p}."\) Persiguiendo esta idea básica, primero hacemos precisa nuestra noción de"\(f \in C D^{1}\) at\(\vec{p}\).”
Un mapa\(f : E^{\prime} \rightarrow E\) es continuamente diferenciable, o de clase\(C D^{1}\) (escrito\(f \in C D^{1}),\) en\(\vec{p}\) iff la siguiente declaración es verdadera:
\[\begin{array}{l}{\text { Given any } \varepsilon>0, \text { there is } \delta>0 \text { such that } f \text { is differentiable on the }} \\ {\text { globe } \overline{G}=\overline{G_{\vec{p}}(\delta)}, \text { with }} \\ {\qquad\|d f(\vec{x} ; \cdot)-d f(\vec{p} ; \cdot)\|<\varepsilon \text { for all } \vec{x} \in \overline{G}.}\end{array}\]
Por Problema 10 en §5, esta definición concuerda con la Definición 1 §5, pero ya no se limita al caso\(E^{\prime}=E^{n}\left(C^{n}\right).\) Ver también Problemas 1 y 2 a continuación.
Ahora obtenemos el siguiente resultado.
Dejar\(E^{\prime}\) y\(E\) estar completo. Si\(f : E^{\prime} \rightarrow E\) es de clase\(C D^{1}\) en\(\vec{p}\) y si\(d f(\vec{p} ; \cdot)\) es biyective (§6), entonces\(f\) es uno a uno en algún globo\(\overline{G}=\overline{G_{\vec{p}}}(\delta).\)
Así\(f\) “localmente” se asemeja a df\((\vec{p} ; \cdot)\) en este sentido.
- Prueba
-
Set\(\phi=d f(\vec{p} ; \cdot)\) y
\[\left\|\phi^{-1}\right\|=\frac{1}{\varepsilon}\]
(cf. Teorema 2 del §6).
Por Definición 1, arreglar\(\delta>0\) para que para\(\vec{x} \in \overline{G}=\overline{G_{\vec{p}}(\delta)}\).
\[\|d f(\vec{x} ; \cdot)-\phi\|<\frac{1}{2} \varepsilon.\]
Luego por la Nota 5 en §2,
\[(\forall \vec{x} \in \overline{G})\left(\forall \vec{u} \in E^{\prime}\right) \quad|d f(\vec{x} ; \vec{u})-\phi(\vec{u})| \leq \frac{1}{2} \varepsilon|\vec{u}|.\]
Ahora arregla cualquiera\(\vec{r}, \vec{s} \in \overline{G}, \vec{r} \neq \vec{s},\) y establece\(\vec{u}=\vec{r}-\vec{s} \neq 0.\) De nuevo, por la Nota 5 en §2,
\[|\vec{u}|=\left|\phi^{-1}(\phi(\vec{u}))\right| \leq\left\|\phi^{-1}\right\||\phi(\vec{u})|=\frac{1}{\varepsilon}|\phi(\vec{u})|;\]
por lo
\[0<\varepsilon|\vec{u}| \leq|\phi(\vec{u})|.\]
Por convexidad,\(\overline{G} \supseteq I=L[\vec{s}, \vec{r}],\) entonces (1) se sostiene para\(\vec{x} \in I, \vec{x}=\vec{s}+t \vec{u}, 0 \leq t \leq 1\).
Al señalar esto, establecer
\[h(t)=f(\vec{s}+t \vec{u})-t \phi(\vec{u}), \quad t \in E^{1}.\]
Entonces para\(0 \leq t \leq 1\),
\[\begin{aligned} h^{\prime}(t) &=D_{\vec{u}} f(\vec{s}+t \vec{u})-\phi(\vec{u}) \\ &=d f(\vec{s}+t \vec{u} ; \vec{u})-\phi(\vec{u}). \end{aligned}\]
(¡Verifica!) Así, por (1) y (2),
\[\begin{aligned} \sup _{0 \leq t \leq 1}\left|h^{\prime}(t)\right| &=\sup _{0 \leq t \leq 1}|d f(\vec{s}+t \vec{u} ; \vec{u})-\phi(\vec{u})| \\ & \leq \frac{\varepsilon}{2}|\vec{u}| \leq \frac{1}{2}|\phi(\vec{u})|. \end{aligned}\]
(¡Explique!) Ahora, por Corolario 1 en el Capítulo 5, §4,
\[|h(1)-h(0)| \leq(1-0) \cdot \sup _{0 \leq t \leq 1}\left|h^{\prime}(t)\right| \leq \frac{1}{2}|\phi(\vec{u})|.\]
Como\(h(0)=f(\vec{s})\) y
\[h(1)=f(\vec{s}+\vec{u})-\phi(\vec{u})=f(\vec{r})-\phi(\vec{u}),\]
obtenemos (incluso si\(\vec{r}=\vec{s})\)
\[|f(\vec{r})-f(\vec{s})-\phi(\vec{u})| \leq \frac{1}{2}|\phi(\vec{u})| \quad(\vec{r}, \vec{s} \in \overline{G}, \vec{u}=\vec{r}-\vec{s}).\]
Pero por la ley del triángulo,
\[|\phi(\vec{u})|-|f(\vec{r})-f(\vec{s})| \leq|f(\vec{r})-f(\vec{s})-\phi(\vec{u})|.\]
Por lo tanto
\[|f(\vec{r})-f(\vec{s})| \geq \frac{1}{2}|\phi(\vec{u})| \geq \frac{1}{2} \varepsilon|\vec{u}|=\frac{1}{2} \varepsilon|\vec{r}-\vec{s}|\]
por (2).
De ahí\(f(\vec{r}) \neq f(\vec{s})\) que siempre\(\overline{G};\) que\(\vec{r} \neq \vec{s}\) en así\(f\) sea uno a uno encendido\(\overline{G},\) como se reclama. \(\quad \square\)
Bajo los supuestos del Teorema 1, los mapas\(f\) y\(f^{-1}\) (el inverso de\(f\) restringido a\(\overline{G}\)) son uniformemente continuos sobre\(\overline{G}\) y\(f[\overline{G}],\) respectivamente.
- Prueba
-
Por (3),
\[\begin{aligned}|f(\vec{r})-f(\vec{s})| & \leq|\phi(\vec{u})|+\frac{1}{2}|\phi(\vec{u})| \\ & \leq|2 \phi(\vec{u})| \\ & \leq 2\|\phi\||\vec{u}| \\ &=2\|\phi\||\vec{r}-\vec{s}| \quad(\vec{r}, \vec{s} \in \overline{G}). \end{aligned}\]
Esto implica una continuidad uniforme para\(f\). (¿Por qué?)
A continuación,\(g=f^{-1}\) vamos\(H=f[\overline{G}]\).
Si se\(\vec{x}, \vec{y} \in H,\) deja\(\vec{r}=g(\vec{x})\) y\(\vec{s}=g(\vec{y});\) así\(\vec{r}, \vec{s} \in \overline{G},\) con\(\vec{x}=f(\vec{r})\) y\(\vec{y}=f(\vec{s}).\) Por lo tanto por (4),
\[|\vec{x}-\vec{y}| \geq \frac{1}{2} \varepsilon|g(\vec{x})-g(\vec{y})|,\]
demostrando todo para\(g,\) también. \(\quad \square\)
Nuevamente,\(f\) se asemeja a\(\phi\) lo que es uniformemente continuo, junto con\(\phi^{-1}\).
II. Introducimos la siguiente definición.
Un mapa\(f :(S, \rho) \rightarrow\left(T, \rho^{\prime}\right)\) está cerrado (abierto) en\(D \subseteq S\) iff, para cualquier\(X \subseteq D\) el conjunto\(f[X]\) está cerrado (abierto) en\(T\) siempre que\(X\) sea así en\(S.\)
Tenga en cuenta que los mapas continuos tienen tal propiedad para imágenes inversas (Problema 15 en el Capítulo 4, §2).
Bajo los supuestos del Teorema 1,\(f\) se cierra\(\overline{G},\) y así el conjunto\(f[\overline{G}]\) se cierra en\(E.\)
De manera similar para el mapa\(f^{-1}\) en\(f[\overline{G}]\).
- Prueba para\(E^{\prime}=E=E^{n}\left(C^{n}\right)\) (para el caso general, ver Problema 6)
-
Dado cualquier cerrado\(X \subseteq \overline{G},\) debemos mostrar que\(f[X]\) está cerrado en\(E.\)
Ahora, como\(\overline{G}\) está cerrado y acotado, es compacto (Teorema 4 del Capítulo 4, §6).
Así también lo es\(X\) (Teorema 1 en el Capítulo 4, §6), y así es\(f[X]\) (Teorema 1 del Capítulo 4, §8).
Por Teorema 2 en el Capítulo 4, §6,\(f[X]\) se cierra, según se requiera. \(\quad \square\)
Para el resto de esta sección, estableceremos\(E^{\prime}=E=E^{n}\left(C^{n}\right)\).
Si\(E^{\prime}=E=E^{n}\left(C^{n}\right)\) en el Teorema 1, con otros supuestos sin cambios, entonces\(f\) está abierto en el globo\(G=G_{\vec{p}}(\delta),\) con\(\delta\) lo suficientemente pequeño.
- Prueba
-
Primero probamos el siguiente lema.
\(f[G]\)contiene un globo\(G_{\vec{q}}(\alpha)\) donde\(\vec{q}=f(\vec{p})\).
- Prueba
-
En efecto, vamos
\[\alpha=\frac{1}{4} \varepsilon \delta,\]
donde\(\delta\) y\(\varepsilon\) son como en la prueba del Teorema 1. (Seguimos la notación y fórmulas de esa prueba.)
Arreglar cualquier\(\vec{c} \in G_{\vec{q}}(\alpha);\)
\[|\vec{c}-\vec{q}|<\alpha=\frac{1}{4} \varepsilon \delta.\]
Establecer\(h=|f-\vec{c}|\)\(E^{\prime}.\) como\(f\) es uniformemente continuo en\(\overline{G},\) así es\(h\).
Ahora bien,\(\overline{G}\) es compacto en el\(E^{n}\left(C^{n}\right);\) Teorema 2 (ii) en el Capítulo 4, §8, rinde un punto\(\vec{r} \in \overline{G}\) tal que
\[h(\vec{r})=\min h[\overline{G}].\]
Afirmamos que\(\vec{r}\) está en\(G\) (el interior de\(\overline{G})\).
De lo contrario,\(|\vec{r}-\vec{p}|=\delta ;\) para por (4),
\[\begin{aligned} 2 \alpha=\frac{1}{2} \varepsilon \delta=\frac{1}{2} \varepsilon|\vec{r}-\vec{p}| & \leq|f(\vec{r})-f(\vec{p})| \\ & \leq|f(\vec{r})-\vec{c}|+|\vec{c}-f(\vec{p})| \\ &=h(\vec{r})+h(\vec{p}). \end{aligned}\]
Pero
\[h(\vec{p})=|\vec{c}-f(\vec{p})|=|\vec{c}-\vec{q}|<\alpha;\]
y así (7) rinde
\[h(\vec{p})<\alpha<h(\vec{r}),\]
contrario a la minimalidad de\(h(\vec{r})\) (ver (6)). Así\(|\vec{r}-\vec{p}|\) no puede igualar\(\delta\).
Lo\(f(\vec{r}) \in f[G].\) obtenemos\(\vec{r} \in G_{\vec{p}}(\delta)=G\) y\(|\vec{r}-\vec{p}|<\delta,\) ahora demostraremos que\(\vec{c}=f(\vec{r}).\)
Para ello, nos fijamos\(\vec{v}=\vec{c}-f(\vec{r})\) y demostramos que\(\vec{v}=\overrightarrow{0}.\) Let
\[\vec{u}=\phi^{-1}(\vec{v}),\]
donde
\[\phi=d f(\vec{p} ; \cdot),\]
como antes. Entonces
\[\vec{v}=\phi(\vec{u})=d f(\vec{p} ; \vec{u}).\]
Con\(\vec{r}\) lo anterior, arregle algunos
\[\vec{s}=\vec{r}+t \vec{u} \quad(0<t<1)\]
con\(t\) tan pequeño que\(\vec{s} \in G\) también. Luego por la fórmula (3),
\[|f(\vec{s})-f(\vec{r})-\phi(t \vec{u})| \leq \frac{1}{2}|t \vec{v}|;\]
también,
\[|f(\vec{r})-\vec{c}+\phi(t \vec{u})|=(1-t)|\vec{v}|=(1-t) h(\vec{r})\]
por nuestra elección de\(\vec{v}, \vec{u}\) y por\(h.\) lo tanto por la ley del triángulo,
\[h(\vec{s})=|f(\vec{s})-\vec{c}| \leq\left(1-\frac{1}{2} t\right) h(\vec{r}).\]
(¡Verifica!)
Como\(0<t<1,\) esto implica\(h(\vec{r})=0\) (de lo contrario,\(h(\vec{s})<h(\vec{r}),\) violar (6)).
Así, de hecho,
\[|\vec{v}|=|f(\vec{r})-\vec{c}|=0,\]
es decir,
\[\vec{c}=f(\vec{r}) \in f[G] \quad \text { for } \vec{r} \in G.\]
Pero\(\vec{c}\) fue un punto arbitrario de\(G_{\vec{q}}(\alpha).\) Por lo tanto
\[G_{\vec{q}}(\alpha) \subseteq f[G],\]
demostrando el lema. \(\quad \square\)
Prueba de Teorema 2. El lema muestra que\(f(\vec{p})\) está en el interior de\(f[G]\) si\(\vec{p}, f, d f(\vec{p} ; \cdot),\) y\(\delta\) son como en el Teorema 1.
Pero la Definición 1 implica que aquí\(f \in C D^{1}\) en todos\(G\) (ver Problema 1).
También,\(d f(\vec{x} ; \cdot)\) es biyectiva para cualquiera\(\vec{x} \in G\) por nuestra elección de\(G\) y Teoremas 1 y 2 en §6.
Por lo tanto,\(f\) mapea todo\(\vec{x} \in G\) en puntos interiores de,\(f[G];\) es decir,\(f\) mapea cualquier conjunto abierto\(X \subseteq G\) en un abierto\(f[X],\) según sea necesario. \(\quad \square\)
Nota 1. Un mapa
\[f :(S, \rho) \underset{\text { onto }}{\longleftrightarrow} (T, \rho^{\prime})\]
es tanto abierto como cerrado (“clopen”) iff\(f^{-1}\) es continuo - ver Problema 15 (iv) (v) en el Capítulo 4, §2, intercambiable\(f\) y\(f^{-1}.\)
Así\(\phi=d f(\vec{p} ; \cdot)\) en Teorema 1 es “clopen” en todos\(E^{\prime}\).
Nuevamente,\(f\) localmente se parece\(d f(\vec{p} ; \cdot)\).
III. El Teorema de la Función Inversa. Ahora seguimos persiguiendo estas ideas.
Bajo los supuestos del Teorema 2, deja\(g\) ser la inversa de\(f_{G}\left(f \text { restricted to } G=G_{\vec{p}}(\delta)\right)\).
Entonces\(g \in C D^{1}\) encendido\(f[G]\) y\(d g(\vec{y} ; \cdot)\) es la inversa de\(d f(\vec{x} ; \cdot)\) siempre\(\vec{x}=g(\vec{y}), \vec{x} \in G.\)
Brevemente: “El diferencial de lo inverso es el inverso del diferencial”.
- Prueba
-
Fijar cualquier\(\vec{y} \in f[G]\) y\(\vec{x}=g(\vec{y}) ;\) así\(\vec{y}=f(\vec{x})\) y\(\vec{x} \in G.\) dejar\(U=d f(\vec{x} ; \cdot).\)
Como se señaló anteriormente,\(U\) es biyectiva para cada uno\(\vec{x} \in G\) por los Teoremas 1 y 2 en §6; así\(V=U^{-1}.\) podremos establecer Debemos demostrar que\(V=d g(\vec{y} ; \cdot).\)
Para ello, da\(\vec{y}\) un incremento arbitrario (variable)\(\Delta \vec{y},\) tan pequeño que\(\vec{y}+\Delta \vec{y}\) permanezca en\(f[G]\) (un conjunto abierto por el Teorema 2).
Como\(g\) y\(f_{G}\) son uno a uno, determina de\(\Delta \vec{y}\) manera única
\[\Delta \vec{x}=g(\vec{y}+\Delta \vec{y})-g(\vec{y})=\vec{t},\]
y viceversa:
\[\Delta \vec{y}=f(\vec{x}+\vec{t})-f(\vec{x}).\]
Aquí\(\Delta \vec{y}\) y\(\vec{t}\) están los incrementos mutuamente correspondientes de\(\vec{y}=f(\vec{x})\) y\(\vec{x}=g(\vec{y}).\) Por continuidad,\(\vec{y} \rightarrow \overrightarrow{0}\) iff\(\vec{t} \rightarrow \overrightarrow{0}.\)
Como\(U=d f(\vec{x} ; \cdot)\),
\[\lim _{\vec{t} \rightarrow \overline{0}} \frac{1}{|\vec{t}|}|f(\vec{x}+\vec{t})-f(\vec{t})-U(\vec{t})|=0,\]
o
\[\lim _{\vec{t} \rightarrow \overrightarrow{0}} \frac{1}{|\vec{t}|}|F(\vec{t})|=0,\]
donde
\[F(\vec{t})=f(\vec{x}+\vec{t})-f(\vec{t})-U(\vec{t}).\]
Como\(V=U^{-1},\) tenemos
\[V(U(\vec{t}))=\vec{t}=g(\vec{y}+\Delta \vec{y})-g(\vec{y}).\]
Así que a partir de (9),
\[\begin{aligned} V(F(\vec{t})) &=V(\Delta \vec{y})-\vec{t} \\ &=V(\Delta \vec{y})-[g(\vec{y}+\Delta \vec{y})-g(\vec{y})]; \end{aligned}\]
es decir,
\[\frac{1}{|\Delta \vec{y}|}|g(\vec{y}+\Delta \vec{y})-g(\vec{y})-V(\Delta \vec{y})|=\frac{|V(F(\vec{t}))|}{|\Delta \vec{y}|}, \quad \Delta \vec{y} \neq \overrightarrow{0}.\]
Ahora, la fórmula (4), con\(\vec{r}=\vec{x}, \vec{s}=\vec{x}+\vec{t},\) y\(\vec{u}=\vec{t},\) muestra que
\[|f(\vec{x}+\vec{t})-f(\vec{x})| \geq \frac{1}{2} \varepsilon|\vec{t}|;\]
es decir,\(|\Delta \vec{y}| \geq \frac{1}{2} \varepsilon|\vec{t}|.\) Por lo tanto por (8),
\[\frac{|V(F(\vec{t}))|}{|\Delta \vec{y}|} \leq \frac{|V(F(\vec{t}) |}{\frac{1}{2} \varepsilon|\vec{t}|}=\frac{2}{\varepsilon}\left|V\left(\frac{1}{|\vec{t}|} F(\vec{t})\right)\right| \leq \frac{2}{\varepsilon}\|V\| \frac{1}{|\vec{t}|}|F(\vec{t})| \rightarrow 0 \text { as } \vec{t} \rightarrow \overrightarrow{0}.\]
Desde\(\vec{t} \rightarrow \overrightarrow{0}\) as\(\Delta \vec{y} \rightarrow \overrightarrow{0}\) (¡cambio de variables!) , la expresión (10) tiende a 0 como\(\Delta \vec{y} \rightarrow \overrightarrow{0}.\)
Por definición, entonces,\(g\) es diferenciable en\(\vec{y},\) con\(d g(\vec{y};)=V=U^{-1}\).
Por otra parte, aquí se aplica el Corolario 3 en §6. Por lo tanto
\[\left(\forall \delta^{\prime}>0\right)\left(\exists \delta^{\prime \prime}>0\right) \quad\|U-W\|<\delta^{\prime \prime} \Rightarrow\left\|U^{-1}-W^{-1}\right\|<\delta^{\prime}.\]
Tomando aquí\(U^{-1}=d g(\vec{y})\) y\(W^{-1}=d g(\vec{y}+\Delta \vec{y}),\) vemos que\(g \in C D^{1}\) cerca\(\vec{y}.\) Esto completa la prueba. \(\quad \square\)
Nota 2. Si\(E^{\prime}=E=E^{n}\left(C^{n}\right),\) la biyectividad de\(\phi=d f(\vec{p} ; \cdot)\) es equivalente a
\[\operatorname{det}[\phi]=\operatorname{det}\left[f^{\prime}(\vec{p})\right] \neq 0\]
(Teorema 1 de §6).
En este caso, el hecho de que\(f\) es uno-a-uno en\(G=G_{\vec{p}}(\delta)\) medio, componentwise (ver Nota 3 en §6), que el sistema de\(n\) ecuaciones
\[f_{i}(\vec{x})=f\left(x_{1}, \ldots, x_{n}\right)=y_{i}, \quad i=1, \ldots, n,\]
tiene una solución única para las\(n\)\(x_{k}\) incógnitas siempre y cuando
\[\left(y_{1}, \ldots, y_{n}\right)=\vec{y} \in f[G].\]
El teorema 3 muestra que esta solución tiene la forma
\[x_{k}=g_{k}(\vec{y}), \quad k=1, \ldots, n,\]
donde los\(g_{k}\) son de clase\(C D^{1}\) en\(f[G]\) siempre que\(f_{i}\) sean de clase\(C D^{1}\) cerca\(\vec{p}\) y det\(\left[f^{\prime}(\vec{p})\right] \neq 0.\) Aquí
\[\operatorname{det}\left[f^{\prime}(\vec{p})\right]=J_{f}(\vec{p}),\]
como en §6.
Así de nuevo\(f\) “localmente” se asemeja a un mapa lineal,\(\phi=d f(\vec{p} ; \cdot)\).
IV. El Teorema de la Función Implícita. Generalizando, ahora nos preguntamos, ¿qué pasa con resolver\(n\) ecuaciones en\(n+m\) incógnitas\(x_{1}, \ldots, x_{n}, y_{1}, \ldots, y_{m}?\) Decir, queremos resolver
\[f_{k}\left(x_{1}, \ldots, x_{n}, y_{1}, \ldots, y_{m}\right)=0, \quad k=1,2, \ldots, n,\]
para las primeras\(n\) incógnitas (o variables) expresándolas\(x_{k},\) así como
\[x_{k}=H_{k}\left(y_{1}, \ldots, y_{m}\right), \quad k=1, \ldots, n,\]
con\(H_{k} : E^{m} \rightarrow E^{1}\) o\(H_{k} : C^{m} \rightarrow C\).
Vamos a establecer\(\vec{x}=\left(x_{1}, \ldots, x_{n}\right), \vec{y}=\left(y_{1}, \ldots, y_{m}\right),\) y
\[(\vec{x}, \vec{y})=\left(x_{1}, \ldots, x_{n}, y_{1}, \ldots, y_{m}\right)\]
para que\((\vec{x}, \vec{y}) \in E^{n+m}\left(C^{n+m}\right)\).
Así, el sistema de ecuaciones (11) simplifica a
\[f_{k}(\vec{x}, \vec{y})=0, \quad k=1, \ldots, n\]
o
\[f(\vec{x}, \vec{y})=\overrightarrow{0},\]
donde\(f=\left(f_{1}, \ldots, f_{n}\right)\) es un mapa de\(E^{n+m}\left(C^{n+m}\right)\) into\(E^{n}\left(C^{n}\right) ; f\) es una función de\(n+m\) variables, pero tiene\(n\) componentes\(f_{k};\) i.e.
\[f(\vec{x}, \vec{y})=f\left(x_{1}, \ldots, x_{n}, y_{1}, \ldots, y_{m}\right)\]
es un vector en\(E^{n}\left(C^{n}\right)\).
Let\(E^{\prime}=E^{n+m}\left(C^{n+m}\right), E=E^{n}\left(C^{n}\right),\) y let\(f : E^{\prime} \rightarrow E\) ser de clase\(C D^{1}\) cerca
\[(\vec{p}, \vec{q})=\left(p_{1}, \ldots, p_{n}, q_{1}, \ldots, q_{m}\right), \quad \vec{p} \in E^{n}\left(C^{n}\right), \vec{q} \in E^{m}\left(C^{m}\right).\]
Deja\([\phi]\) ser la\(n \times n\) matriz
\[\left(D_{j} f_{k}(\vec{p}, \vec{q})\right), \quad j, k=1, \ldots, n.\]
Si\(\operatorname{det}[\phi] \neq 0\) y si\(f(\vec{p}, \vec{q})=\overrightarrow{0},\) entonces hay conjuntos abiertos
\[P \subseteq E^{n}\left(C^{n}\right) \text { and } Q \subseteq E^{m}\left(C^{m}\right),\]
con\(\vec{p} \in P\) y\(\vec{q} \in Q,\) para el que hay un mapa único
\[H : Q \rightarrow P\]
con
\[f(H(\vec{y}), \vec{y})=\overrightarrow{0}\]
para todos\(\vec{y} \in Q;\) además,\(H \in C D^{1}\) en\(Q\).
Así\(\vec{x}=H(\vec{y})\) es una solución de (11) en forma de vector.
- Prueba
-
Con la notación anterior, establezca
\[F(\vec{x}, \vec{y})=(f(\vec{x}, \vec{y}), \vec{y}), \quad F : E^{\prime} \rightarrow E^{\prime}.\]
Entonces
\[F(\vec{p}, \vec{q})=(f(\vec{p}, \vec{q}), \vec{q})=(\overrightarrow{0}, \vec{q}),\]
ya que\(f(\vec{p}, \vec{q})=\overrightarrow{0}\).
\((\vec{p}, \vec{q}),\)Tan\(f \in C D^{1}\) cerca como está\(F\) (verificar componentwise vía Problema 9 (ii) en §3 y Definición 1 de §5).
Por Teorema 4, §3,\(\operatorname{det}\left[F^{\prime}(\vec{p}, \vec{q})\right]=\operatorname{det}[\phi] \neq 0\) (¡explique!).
Así Teorema 1 anterior muestra que\(F\) es uno a uno en algún globo\(G\) sobre\((\vec{p}, \vec{q}).\)
Claramente\(G\) contiene un intervalo abierto sobre\((\vec{p}, \vec{q}).\) Lo denotamos por\(P \times Q\) donde\(\vec{p} \in P, \vec{q} \in Q ; P\) está abierto en\(E^{n}\left(C^{n}\right)\) y\(Q\) está abierto en\(E^{m}\left(C^{m}\right).\)
Por Teorema 3,\(F_{P \times Q}\) (\(F\)restringido a\(P \times Q)\) tiene una inversa
\[g : A \underset{\text { onto }}{\longleftrightarrow} P \times Q,\]
donde\(A=F[P \times Q]\) está abierto en\(E^{\prime}\) (Teorema 2), y\(g \in C D^{1}\) en\(A.\) Dejar que el mapa\(u=\left(g_{1}, \ldots, g_{n}\right)\) comprende los primeros\(n\) componentes de\(g\) (exactamente como\(f\) comprende los primeros\(n\) componentes de\(F )\).
Entonces
\[g(\vec{x}, \vec{y})=(u(\vec{x}, \vec{y}), \vec{y})\]
exactamente como\(F(\vec{x}, \vec{y})=(f(\vec{x}, \vec{y}), \vec{y}).\) También,\(u : A \rightarrow P\) es de clase\(C D^{1}\) encendido\(A,\) como\(g\) es (¡explique!).
Ahora establece
\[H(\vec{y})=u(\overrightarrow{0}, \vec{y});\]
aquí\(\vec{y} \in Q,\) mientras
\[(\overrightarrow{0}, \vec{y}) \in A=F[P \times Q],\]
para\(F\) conservas\(\vec{y}\) (las últimas\(m\) coordenadas). También se establece
\[\alpha(\vec{x}, \vec{y})=\vec{x}.\]
Entonces\(f=\alpha \circ F\) (¿por qué?) , y
\[f(H(\vec{y}), \vec{y})=f(u(\overrightarrow{0}, \vec{y}), \vec{y})=f(g(\overrightarrow{0}, \vec{y}))=\alpha(F(g(\overrightarrow{0}, \vec{y}))=\alpha(\overrightarrow{0}, \vec{y})=\overrightarrow{0}\]
por nuestra elección de\(\alpha\) y\(g\) (inverso a\(F).\) Así
\[f(H(\vec{y}), \vec{y})=\overrightarrow{0}, \quad \vec{y} \in Q,\]
según se desee.
Además, como\(H(\vec{y})=u(\overrightarrow{0}, \vec{y}),\) tenemos
\[\frac{\partial}{\partial y_{i}} H(\vec{y})=\frac{\partial}{\partial y_{i}} u(\overrightarrow{0}, \vec{y}), \quad \vec{y} \in Q, i \leq m.\]
Como\(u \in C D^{1},\) todos\(\partial u / \partial y_{i}\) son continuos (Definición 1 en §5); por lo tanto también lo son los\(\partial H / \partial y_{i}.\) Así por Teorema 3 en §3,\(H \in C D^{1}\) on\(Q.\)
Por último,\(H\) es único por lo dado\(P, Q;\) por
\[\begin{aligned} f(\vec{x}, \vec{y})=\overrightarrow{0} & \Longrightarrow(f(\vec{x}, \vec{y}), \vec{y})=(\overrightarrow{0}, \vec{y}) \\ & \Longrightarrow F(\vec{x}, \vec{y})=(\overrightarrow{0}, \vec{y}) \\ & \Longrightarrow g(F(\vec{x}, \vec{y}))=g(\overrightarrow{0}, \vec{y}) \\ & \Longrightarrow(\vec{x}, \vec{y})=g(\overrightarrow{0}, \vec{y})=(u(\overrightarrow{0}, \vec{y}), \vec{y}) \\ & \Longrightarrow \vec{x}=u(\overrightarrow{0}, \vec{y})=H(\vec{y}). \end{aligned}\]
Así\(f(\vec{x}, \vec{y})=\overrightarrow{0}\) implica\(\vec{x}=H(\vec{y});\) que así\(H(\vec{y})\) es la única solución para\(\vec{x}. \quad \square\)
Nota 3. \(H\)se dice que está implícitamente definido por la ecuación\(f(\vec{x}, \vec{y})=\overrightarrow{0}.\) En este sentido decimos que\(H(\vec{y})\) es una función implícita, dada por\(f(\vec{x}, \vec{y})=\overrightarrow{0}\).
Del mismo modo, bajo supuestos adecuados,\(f(\vec{x}, \vec{y})=\overrightarrow{0}\) define\(\vec{y}\) como una función de\(\vec{x}.\)
Nota 4. Si bien\(H\) es único para un vecindario dado\(P \times Q\) de\((\vec{p}, \vec{q}),\) otra función implícita puede resultar si\(P \times Q\) o\((\vec{p}, \vec{q})\) se cambia.
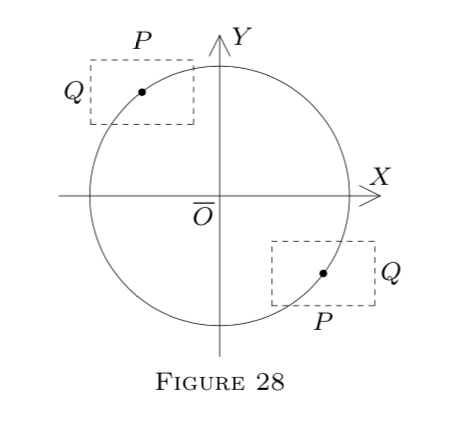
Por ejemplo, vamos
\[f(x, y)=x^{2}+y^{2}-25\]
(un polinomio; de ahí\(f \in C D^{1}\) en todo\(E^{2}).\) Geométricamente,\(x^{2}+y^{2}-25=0\) describe un círculo.
Resolviendo para\(x,\) obtenemos\(x=\pm \sqrt{25-y^{2}}.\) Así tenemos dos funciones:
\[H_{1}(y)=+\sqrt{25-y^{2}}\]
y
\[H_{2}(y)=-\sqrt{25-y^{2}}.\]
Si\(P \times Q\) está en la parte superior del círculo, la función resultante es\(H_{1}.\) De lo contrario, es\(H_{2}.\) Ver Figura 28.
V. Diferenciación implícita. El teorema 4 sólo afirma la existencia (y singularidad) de una solución, pero no muestra cómo encontrarla, en general.
El conocimiento mismo que\(H \in C D^{1}\) existe, sin embargo, nos permite utilizar su derivado o parciales y calcularlo por diferenciación implícita, conocida a partir del cálculo.
a) Que\(f(x, y)=x^{2}+y^{2}-25=0,\) lo anterior.
Esta vez tratando\(y\) como una función implícita de\(x, y=H(x),\) y escribiendo\(y^{\prime}\) para\(H^{\prime}(x),\) diferenciamos ambos lados de (x^ {2} +y^ {2} -25=0\) con respecto al\(x,\) uso de la regla de cadena para el término\(y^{2}=[H(x)]^{2}\).
Esto rinde\(2 x+2 y y^{\prime}=0,\) de donde\(y^{\prime}=-x / y\).
En realidad (ver Nota 4), están involucradas dos funciones:\(y=\pm \sqrt{25-x^{2}};\) pero ambas satisfacen\(x^{2}+y^{2}-25=0;\) por lo que el resultado\(y^{\prime}=-x / y\) se aplica a ambas.
Por supuesto, este método sólo es posible si\(y^{\prime}\) se sabe que la derivada existe. Es por ello que el Teorema 4 es importante.
b) Dejar
\[f(x, y, z)=x^{2}+y^{2}+z^{2}-1=0, \quad x, y, z \in E^{1}.\]
De nuevo\(f\) satisface Teorema 4 para adecuado\(x, y,\) y\(z\).
Ajuste\(z=H(x, y),\) diferenciar la ecuación\(f(x, y, z)=0\) parcialmente con respecto a\(x\) y A\(y.\) partir de las dos ecuaciones resultantes, obtener\(\frac{\partial z}{\partial x}\) y\(\frac{\partial z}{\partial y}\).


