7.6.E: Problemas en las Medidas y Medidas Exteriores
- Page ID
- 114021
Mostrar que las fórmulas (1) y (2) son equivalentes.
[Consejos: (i) Supongamos (1) y dejar\(X \subseteq A, Y \subseteq-A .\)
Como\(X\) en (1) es arbitrario, podemos reemplazarlo por\(X \cup Y.\) Simplificar, obtener (2) al señalar que\(X \cap A=X, X \cap-A=\emptyset, Y \cap A=\emptyset,\) y\(Y \cap-A=Y\).
ii) Asumir (2). Tome cualquiera\(X\) y sustituya\(X \cap A\) y\(X-A\) para\(X\) y\(Y\) en (2).]
Dado un espacio de medida exterior\(\left(S, \mathcal{M}^{*}, m^{*}\right)\) y\(A \subseteq S,\) conjunto
\[A \cap \mathcal{M}^{*}=\left\{A \cap X | X \in \mathcal{M}^{*}\right\}\] (¡SÍMBOLO!)
(todos los conjuntos del formulario\(A \cap X\) con\(X \in \mathcal{M}^{*}\)).
Demostrar que\(A \cap \mathcal{M}^{*}\) es un\(\sigma\) -campo en\(A,\) y\(m^{*}\) es\(\sigma\) -aditivo en él. (¡SÍMBOLO!)
[Pista: Use Lemma 4, con\(X_{k}=A \cap A_{k} \in A \cap \mathcal{M}^{*}\).] (¡SÍMBOLO!)
Prueba Lemmas 1 y 2, usando la fórmula (1).
Demostrar Corolario 1.
Verificar los Ejemplos (b), (c) y (d). ¿Por qué también es\(m\) una medida exterior?
[Pista: Usar el Corolario 2 en §5.]
Rellene todos los datos (inducción, etc.) en las pruebas de esta sección.
Verificar que\(m^{*}\) sea una medida externa y describa\(\mathcal{M}^{*}\) bajo cada una de las siguientes condiciones.
(a)\(m^{*} A=1\) si\(\emptyset \subset A \subseteq S; m^{*} \emptyset=0\).
b)\(m^{*} A=1\) si\(\emptyset \subset A \subset S; m^{*} S=2; m^{*} \emptyset=0\).
c)\(m^{*} A=0\) si\(A \subseteq S\) es contable; de\(m^{*} A=1\) lo contrario (\(S\)es incontable).
d)\(S=N\) (naturales);\(m^{*} A=1\) si\(A\) es infinito;\(m^{*} A=\frac{n}{n+1}\) si\(A\) tiene\(n\) elementos.
Demostrar lo siguiente.
(i) Una medida externa\(m^{*}\) es\(\mathcal{M}^{*}\) -regular (Definición 5 en §5) iff
\[(\forall A \subseteq S)\left(\exists B \in \mathcal{M}^{*}\right) \quad A \subseteq B \text { and } m^{*} A=m B.\]
\(B\) se denomina cobertura medible de\(A\).
[Pista: Si
\[m^{*} A=\inf \left\{m X | A \subseteq X \in \mathcal{M}^{*}\right\},\]
luego se
\[(\forall n)\left(\exists X_{n} \in \mathcal{M}^{*}\right) \quad A \subseteq X_{n} \text { and } m X_{n} \leq m^{*} A+\frac{1}{n}.\]
establece\(B=\bigcap_{n=1}^{\infty} X_{n}\).]
(ii) Si\(m^{*}\) es como en la Definición 3 de §5, con\(\mathcal{C} \subseteq \mathcal{M}^{*},\) entonces\(m^{*}\) es\(\mathcal{M}^{*}\) -regular.
Mostrar que si\(m^{*}\) es\(\mathcal{M}^{*}\) -regular (Problema 7), se deja continuo.
[Consejos:\(\left\{A_{n}\right\} \uparrow;\) Deja que\(B_{n}\) sea una portada medible de\(A_{n};\) conjunto
\[C_{n}=\bigcap_{k=n}^{\infty} B_{k}.\]
Verifica eso\(\left\{C_{n}\right\} \uparrow, B_{n} \supseteq C_{n} \supseteq A_{n},\) y\(m C_{n}=m^{*} A_{n}\).
Por la continuidad izquierda de\(m\) (Teorema 2 en §4),
\[\lim m^{*} A_{n}=\lim m C_{n}=m \bigcup_{n=1}^{\infty} C_{n} \geq m^{*} \bigcup_{n=1}^{\infty} A_{n}.\]
Demostrar la desigualdad inversa también.]
Continuando Problemas 6-8, verificar lo siguiente.
(i) En 6 (a), con\(S=N, m^{*}\) es\(\mathcal{M}^{*}\) -regular, pero no correcto continuo.
Pista: Tomar\(A_{n}=\{x \in N | x \geq n\}\).
(ii) En 6 (b), con no\(S=N, m^{*}\) es ni\(\mathcal{M}^{*}\) -regular ni se deja continuo.
(iii) En 6 (d), no\(m^{*}\) es\(\mathcal{M}^{*}\) -regular; sin embargo, se deja continuo. (Por lo tanto, el problema 8 no es una condición necesaria.)
En Problema 2, deje\(n^{*}\) ser la restricción de\(m^{*}\)\(2^{A}.\) Probarse lo siguiente.
(a)\(n^{*}\) es una medida externa en\(A\).
b)\(A \cap \mathcal{M}^{*} \subseteq \mathcal{N}^{*}=\left\{n^{*} \text {-measurable sets}\right\}\). (¡SÍMBOLO!)
(c)\(A \cap \mathcal{M}^{*}=\mathcal{N}^{*}\) si\(A \in \mathcal{M}^{*},\) o si\(m^{*}\) es\(\mathcal{M}^{*}\) -regular (ver Problema 7) y finito. (¡SÍMBOLO!)
(d)\(n^{*}\) es\(\mathcal{N}^{*}\) -regular si\(m^{*}\) es\(\mathcal{M}^{*}\) -regular.
Mostrar que si\(m^{*}\) es\(\mathcal{M}^{*}\) -regular y finito, entonces\(A \subseteq S\) es\(m^{*}\) -medible iff
\[m S=m^{*} A+m^{*}(-A).\]
[Pista: Supongamos lo último. Por Problema 7,
\[(\forall X \subseteq S)\left(\exists B \in \mathcal{M}^{*}, B \supseteq X\right) \quad m^{*} X=m B;\]
así
\[m^{*} A=m^{*}(A \cap B)+m^{*}(A-B).\]
Similarmente para\(-A.\) Deducir que de
\[m^{*}(A \cap B)+m^{*}(A-B)+m^{*}(B-A)+m^{*}(-A-B)=m S=m B+m(-B);\]
ahí que
\[m^{*} X=m B \geq m^{*}(B \cap A)+m^{*}(B-A) \geq m^{*}(X \cap A)+m^{*}(X-A),\]
así\(A \in \mathcal{M}^{*}\).]
Usando el Problema 15 en §5, demuestre que si\(m^{*}\) tiene el CP entonces cada conjunto abierto\(G \subseteq S\) está adentro\(\mathcal{M}^{*}\).
[Esquema: Mostrar que
\[(\forall X \subseteq G)(\forall Y \subseteq-G) \quad m^{*}(X \cup Y) \geq m^{*} X+m^{*} Y,\]
asumiendo\(m^{*} X<\infty.\) (¿Por qué?) Establecer
\[D_{0}=\{x \in X | \rho(x,-G) \geq 1\}\]
y
\[D_{k}=\left\{x \in X | \frac{1}{k+1} \leq \rho(x,-G)<\frac{1}{k}\right\}, \quad k \geq 1.\]
Probarlo
\[X=\bigcup_{k=0}^{\infty} D_{k}\]
y
\[\rho\left(D_{k}, D_{k+2}\right)>0;\]
así por el Problema 15 en §5,
\[\sum_{n=0}^{\infty} m^{*} D_{2 n}=m^{*} \bigcup_{n=0}^{\infty} D_{2 n} \leq m^{*} \bigcup_{n=0}^{\infty} D_{n}=m^{*} X<\infty.\]
Similarmente,
\[\sum_{n=0}^{\infty} m^{*} D_{2 n+1} \leq m^{*} X<\infty.\]
De ahí
\[\sum_{n=0}^{\infty} m^{*} D_{n}<\infty;\]
que así
\[\lim _{n \rightarrow \infty} \sum_{k=n}^{\infty} m^{*} D_{k}=0.\]
(¿por qué?) Por lo tanto
\[(\forall \varepsilon>0)(\exists n) \sum_{k=n}^{\infty} m^{*} D_{k}<\varepsilon.\]
También,
\[X=\bigcup_{k=0}^{\infty} D_{k}=\bigcup_{k=0}^{n-1} D_{k} \cup \bigcup_{k=n}^{\infty} D_{k};\]
así
\[m^{*} X \leq m^{*} \bigcup_{k=0}^{n-1} D_{k}+\sum_{k=n}^{\infty} m^{*} D_{k}<m^{*} \bigcup_{k=0}^{n-1} D_{k}+\varepsilon.\]
Añadiendo\(m^{*} Y\) en ambos lados, obtener
\[m^{*} X+m^{*} Y \leq m^{*} \bigcup_{k=0}^{n-1} D_{k}+m^{*} Y+\varepsilon.\]
Por otra parte,
\[\rho\left(\bigcup_{k=0}^{n-1} D_{k}, Y\right)>0,\]
para\(Y \subseteq-G\) y
\[\rho\left(D_{k},-G\right) \geq \frac{1}{k+1}.\]
De ahí por el CP,
\[m^{*} Y+\sum_{k=0}^{n-1} m^{*} D_{k}=m^{*}\left(Y \cup \bigcup_{k=0}^{n-1} D_{k}\right)<m^{*}(Y \cup X).\]
(¿Por qué?) Combinando con (iii), obtener
\[m^{*} X+m^{*} Y \leq m^{*}(X \cup Y)+\varepsilon.\]
Ahora vamos\(\varepsilon \rightarrow 0\).]
\(\Rightarrow\)Mostrar que si\(m : \mathcal{M} \rightarrow E^{*}\) es una medida, hay\(P \in \mathcal{M},\) con
\[m P=\max \{m X | X \in \mathcal{M}\}.\]
[Pista: Dejar
\[k=\sup \{m X | X \in \mathcal{M}\}\]
entrar\(E^{*}.\) Como\(k \geq 0,\) hay una secuencia\(r_{n} \nearrow k, r_{n}<k.\) (Si se\(k=\infty,\) establece\(r_{n}=n;\) si\(\left.k<\infty, r_{n}=k-\frac{1}{n}.\right)\) Por propiedades lub,
\[(\forall n)\left(\exists X_{n} \in \mathcal{M}\right) \quad r_{n}<m X_{n} \leq k,\]
con\(\left\{X_{n}\right\} \uparrow\) (Problema 9 en §3). Establecer
\[P=\bigcup_{n=1}^{\infty} X_{n}.\]
Mostrar eso
\[m P=\lim _{n \rightarrow \infty} m X_{n}=k.]\]
\(\Rightarrow^{*}\)Dada una medida\(m : \mathcal{M} \rightarrow E^{*},\) dejemos
\[\overline{\mathcal{M}}=\{\text {all sets of the form } X \cup Z \text { where } X \in \mathcal{M} \text { and } Z \text { is } m \text{-null}\}.\]
Demostrar que\(\overline{\mathcal{M}}\) es un\(\sigma\) anillo\(\supseteq \mathcal{M}\).
[Pista: Para probar que
\[(\forall A, B \in \overline{\mathcal{M}}) \quad A-B \in \overline{\mathcal{M}},\]
supongamos primero\(A \in \mathcal{M}\) y\(B\) es “nulo”, es decir,\(B \subseteq U \in \mathcal{M}, m U=0\).
Mostrar que
\[A-B=X \cup Z,\]
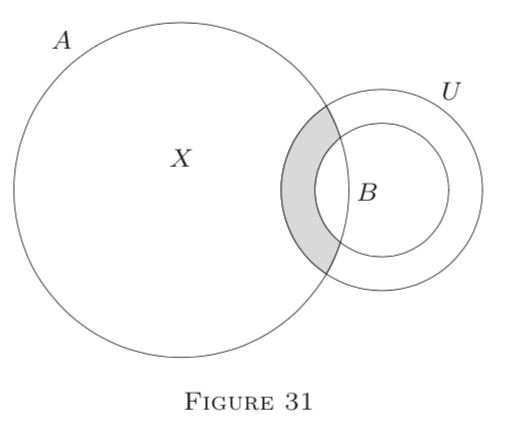
con\(X=A-U \in \mathcal{M}\) y\(Z=A \cap U-B m\) -null (\(Z\)está sombreado en la Figura 31).
A continuación, si\(A, B \in \overline{\mathcal{M}},\) vamos\(A=X \cup Z\)\(B=X^{\prime} \cup Z^{\prime},\) donde\(X, X^{\prime} \in \mathcal{M}\) y\(Z, Z^{\prime}\) son\(m\) -nulos. De ahí
\[\begin{aligned} A-B &=(X \cup Z)-B \\ &=(X-B) \cup(Z-B) \\ &=(X-B) \cup Z^{\prime \prime}, \end{aligned}\]
donde
\[Z^{\prime \prime}=Z-B\]
es\(m\) -null. También,\(B=X^{\prime} \cup Z^{\prime}\) implica
\[X-B=\left(X-X^{\prime}\right)-Z^{\prime} \in \overline{\mathcal{M}},\]
por la primera parte de la prueba.
Deducir eso
\[A-B=(X-B) \cup Z^{\prime \prime} \in \overline{\mathcal{M}}\]
(después de verificar el cierre bajo sindicatos).]
\(\Rightarrow^{*}\)Continuando Problema 14, defina\(\overline{m} : \overline{\mathcal{M}} \rightarrow E^{*}\) configurando\(\overline{m} A=m X\) siempre\(A=X \cup Z,\) con\(X \in \mathcal{M}\) y\(Z\)\(m\) -null. (Demostrar que\(\overline{m} A\) no depende de la representación particular de\(A\) as\(X \cup Z\).)
Demostrar lo siguiente.
(i)\(\overline{m}\) es una medida completa (llamada terminación de\(m\)), con\(\overline{m}=m\) on\(\mathcal{M}.\)
(ii)\(\overline{m}\) es la extensión menos completa de\(m;\) eso es, si\(n : \mathcal{N} \rightarrow E^{*}\) es otra medida completa, con\(\mathcal{M} \subseteq \mathcal{N}\) y\(n=m\) sobre \(\mathcal{M},\)entonces\(\overline{\mathcal{M}} \subseteq \mathcal{N}\) y\(n=\overline{m}\) en\(\overline{\mathcal{M}}.\)
(iii)\(m=\overline{m}\) iff\(m\) está completo.
Mostrar que si\(m : \mathcal{M}^{*} \rightarrow E^{*}\) es inducido por una medida externa\(\mathcal{M}^{*}\) -regular\(\mu^{*},\) entonces\(m\) es igual a su extensión\(m^{\prime}\) y finalización de Lebesgue\(\overline{m}\) (ver Problema 15).
[Pista: Por Definición 3 en §5,\(m\) induce una medida externa\(m^{*}.\) Por Teorema 3 en §5,
\[m^{*} A=\inf \left\{m X | A \subseteq X \in \mathcal{M}^{*}\right\}=\mu^{*} A\]
(para\(\mu^{*}\) es\(\mathcal{M}^{*}\) -regular).
A medida\(m^{*}=\mu^{*},\) que obtenemos\(m^{\prime}=m.\) También,\(m=\overline{m},\) por Problema 15 (iii).]
Demostrar que si una medida\(\mu : \mathcal{M} \rightarrow E^{*}\) es\(\sigma\) -finita (Definición 4 en §5), con\(S \in \mathcal{M},\) entonces su extensión Lebesgue\(m : \mathcal{M}^{*} \rightarrow E^{*}\) equivale a su finalización\(\overline{\mu}\) (ver Problema 15).
[Esquema: Baste probar\(\mathcal{M}^{*} \subseteq \overline{\mathcal{M}}.\) (¿Por qué?)
Para empezar, vamos\(A \in \mathcal{M}^{*}, m A<\infty.\) Por Problema 12 en §5,
\[(\exists B \in \mathcal{M}) \quad A \subseteq B \text { and } m^{*} A=m A=m B<\infty;\]
así
\[m(B-A)=m B-m A=0.\]
También,
\[(\exists H \in \mathcal{M}) \quad B-A \subseteq H \text { and } \mu H=m(B-A)=0.\]
Así\(B-A\) es\(\mu\) -null; entonces\(B-A \in \overline{\mathcal{M}}.\) (¿Por qué?) Deducir que
\[A=B-(B-A) \in \overline{\mathcal{M}}.\]
Así\(\overline{\mathcal{M}}\) contiene cualquiera\(A \in \mathcal{M}^{*}\) con\(m A<\infty.\) Use la\(\sigma\) -finitud de\(\mu\) para mostrar
\[\left.\left(\forall x \in \mathcal{M}^{*}\right)\left(\exists\left\{A_{n}\right\} \subseteq \mathcal{M}^{*}\right) \quad m A_{n}<\infty \text { and } X=\bigcup_{n} A_{n} \in \overline{\mathcal{M}}.\right]\]

