8.4: Integración de Funciones Elementales
- Page ID
- 113792
En el Capítulo 5, la integración se trató como antidiferenciación. Ahora adoptamos otro enfoque médico-teórico.
La teoría original de Lebesgue se basó en la medida de Lebesgue (Capítulo 7, §8). El tratamiento moderno más general desarrolla la integral para funciones\(f : S \rightarrow E\) en un espacio de medida arbitraria. De ahora en adelante,\((S, \mathcal{M}, m)\) es fijo, y el espacio de rango\(E\) es\(E^{1}, E^{*}, C, E^{n},\) u otro espacio normado completo. Recordemos que en tal espacio,\(\sum_{i}\left|a_{i}\right|<\infty\) implica que\(\sum a_{i}\) converge y es permutable (Capítulo 7, §2).
Comenzamos con mapas elementales, incluyendo mapas simples como caso especial.
\(f : S \rightarrow E\)Sea elemental,\(A \in \mathcal{M};\) así\(f=a_{i}\) sucesivamente\(A_{i}\) para algunos\(\mathcal{M}\) -partición
\[A=\bigcup_{i} A_{i} \text { (disjoint).}\]
(Tenga en cuenta que puede haber muchas de esas particiones.)
Decimos que\(f\) es integrable (con respecto a\(m\)), o\(m\) -integrable, en\(A\) iff
\[\sum\left|a_{i}\right| m A_{i}<\infty.\]
(La notación "\(|a_{i}| m A_{i}\)" siempre tiene sentido por nuestras convenciones (2*) en el Capítulo 4, §4.) Si\(m\) es Lebesgue medida, entonces decimos que\(f\) es Lebesgue integrable, o L-integrable.
Luego definimos\(\int_{A} f,\) la\(m\) -integral de\(f\) on\(A,\) by
\[\int_{A} f=\int_{A} f d m=\sum_{i} a_{i} m A_{i}.\]
(Se utiliza la notación\(dm\) "" para especificar la medida\(m\).)
La notación “clásica” para\(\int_{A} f d m\) is\(\int_{A} f(x) d m(x)\).
Nota 1. La suposición
\[\sum\left|a_{i}\right| m A_{i}<\infty\]
implica
\[(\forall i) \quad\left|a_{i}\right| m A_{i}<\infty;\]
entonces\(a_{i}=0\) si\(m A_{i}=\infty,\) y\(m A_{i}=0\) si\(|a_{i}|=\infty.\) Así por nuestras convenciones, todos los términos “malos”\(a_{i} m A_{i}\) desaparecen. De ahí que la suma en (1) tenga sentido y sea finita.
Nota 2. Esta suma también es independiente de la elección particular de\(\{A_{i}\}.\) Para si\(\{B_{k}\}\) es otra\(\mathcal{M}\) -partición de\(A,\) con\(f=b_{k}\) on\(B_{k},\) say, entonces\(f=a_{i}=b_{k}\) on\(A_{i} \cap B_{k}\) siempre que\(A_{i} \cap B_{k} \neq \emptyset.\) También,
\[(\forall i) \quad A_{i}=\bigcup_{k}\left(A_{i} \cap B_{k}\right) \text { (disjoint);}\]
por lo
\[(\forall i) \quad a_{i} m A_{i}=\sum_{k} a_{i} m(A_{i} \cap B_{k}),\]
y por lo tanto (ver Teorema 2 del Capítulo 7, §2, y Problema 11 ahí)
\[\sum_{i} a_{i} m A_{i}=\sum_{i} \sum_{k} a_{i} m\left(A_{i} \cap B_{k}\right)=\sum_{k} \sum_{i} b_{k} m\left(A_{i} \cap B_{k}\right)=\sum_{k} b_{k} m B_{k}.\]
(¡Explique!)
Esto hace que nuestra definición (1) sea inequívoca y nos permite elegir cualquier\(\mathcal{M}\) -partición\(\{A_{i}\},\) con\(f\) constante en cada una\(A_{i},\) al formar integrales (1).
Dejemos\(f : S \rightarrow E\) ser elementales e integrables en\(A \in \mathcal{M}.\) Entonces las siguientes afirmaciones son ciertas.
(i)\(|f|<\infty\) a.e. en\(A.\)
(ii)\(f\) y\(|f|\) son elementales e integrables en cualquier\(\mathcal{M}\) conjunto\(B \subseteq A,\) y
\[\left|\int_{B} f\right| \leq \int_{B}|f| \leq \int_{A}|f|.\]
(iii) El conjunto\(B=A(f \neq 0)\) es\(\sigma\) -finito (Definición 4 en el Capítulo 7, §5), y
\[\int_{A} f=\int_{B} f.\]
iv) Si\(f=a\) (constante) en\(A\),
\[\int_{A} f=a \cdot m A.\]
v)\(\int_{A}|f|=0\) iff\(f=0\) a.e. on\(A\).
vi) Si\(m Q=0,\) entonces
\[\int_{A} f=\int_{A-Q} f\]
(por lo que podemos descuidar conjuntos de medida 0 en integrales).
(vii) Para cualquiera\(k\) en el campo escalar de\(E, k f\) es elemental e integrable, y
\[\int_{A} k f=k \int_{A} f.\]
Tenga en cuenta que si\(f\) se valora escalar,\(k\) puede ser un vector. Si\(E=E^{*},\) asumimos\(k \in E^{1}.\)
- Prueba
-
(i) Por la Nota 1,\(|f|=|a_{i}|=\infty\) sólo en aquellos\(A_{i}\) con\(m A_{i}=0.\) Let\(Q\) be la unión de todos los tales\(A_{i}.\) Entonces\(m Q=0\) y\(|f|<\infty\) al\(A-Q,\) probar (i).
(ii) Si\(\{A_{i}\}\) es una\(\mathcal{M}\) partición -de\(A,\{B \cap A_{i}\}\) es uno para\(B.\) (¡Verifica!) Tenemos\(f=a_{i}\) y\(|f|=|a_{i}|\) en\(B \cap A_{i} \subseteq A_{i}\).
Además,
\[\sum\left|a_{i}\right| m\left(B \cap A_{i}\right) \leq \sum\left|a_{i}\right| m A_{i}<\infty.\]
(¿Por qué?) Así\(f\) y\(|f|\) son elementales e integrables en\(B,\) y (ii) siguen fácilmente por la fórmula (1).
iii) Por la Nota 1,\(f=0\) sobre\(A_{i}\) si\(m A_{i}=\infty.\) Así\(f \neq 0\) en\(A_{i}\) sólo si\(m A_{i}<\infty\). \(\{A_{i_{k}}\}\)Sea la subsecuencia de aquellos\(A_{i}\) en los que\(f \neq 0;\) así
\[(\forall k) \quad m A_{i_{k}}<\infty.\]
Además,
\[B=A(f \neq 0)=\bigcup_{k} A_{i_{k}} \in \mathcal{M} \text{ (}\sigma \text {-finite!).}\]
Por (ii),\(f\) es elemental e integrable en\(B.\) También,
\[\int_{B} f=\sum_{k} a_{i_{k}} m A_{i_{k}},\]
mientras
\[\int_{A} f=\sum_{i} a_{i} m A_{i}.\]
Estas sumas difieren sólo en términos con\(a_{i}=0.\) Así (iii) sigue.
Se deja al lector la prueba de (iv) - (vii). \(\quad \square\)
Nota 3. Si\(f : S \rightarrow E^{*}\) es elemental y signo-constante encendido\(A,\) también permitimos que
\[\int_{A} f=\sum_{i} a_{i} m A_{i}=\pm \infty.\]
Así aquí\(\int_{A} f\) existe aunque no\(f\) sea integrable. Aparte de las afirmaciones de integrabilidad y\(\sigma\) -finitud, el Corolario 1 (ii) - (vii) se sostiene para tal\(f\), con las mismas pruebas.
Let\(m\) Be Lebesgue mide en\(E^{1}.\) Definir\(f=1\) sobre\(R\) (racionales) y\(f=0\) en\(E^{1}-R ;\) ver Capítulo 4, §1, Ejemplo (c). Let\(A=[0,1].\)
Por Corolario 1 en el Capítulo 7, §8,\(A \cap R \in \mathcal{M}^{*}\) y\(m(A \cap R)=0.\) También,\(A-R \in \mathcal{M}^{*}\).
Así\(\{A \cap R, A-R\}\) es una\(\mathcal{M}^{*}\) partición -de\(A,\) con\(f=1\) encendido\(A \cap R\) y\(f=0\) encendido\(A-R.\)
Por lo tanto,\(f\) es elemental e integrable en\(A,\) y
\[\int_{A} f=1 \cdot m(A \cap R)+0 \cdot m(A-R)=0.\]
Así\(f\) es L-integrable (aunque no es en ninguna parte continua).
(i) Si\(f : S \rightarrow E\) es elemental e integrable o elemental y no negativo en\(A \in \mathcal{M},\) entonces
\[\int_{A} f=\sum_{k} \int_{B_{k}} f\]
para cualquier\(\mathcal{M}\) -partición\(\left\{B_{k}\right\}\) de\(A\).
(ii) Si\(f\) es elemental e integrable en cada conjunto\(B_{k}\) de una\(\mathcal{M}\) partición finita
\[A=\bigcup_{k} B_{k},\]
es elemental e integrable en todos\(A,\) y (2) se sostiene de nuevo.
- Prueba
-
(i) Si\(f\) es elemental e integrable o elemental y no negativo en\(A=\bigcup_{k} B_{k},\) él seguramente es así en cada uno\(B_{k}\) por el Corolario 2 de §1 y Corolario 1 (ii) anterior.
Así para cada uno\(k,\) podemos fijar una\(\mathcal{M}\) -partición\(B_{k}=\bigcup_{i} A_{k i},\) con\(f\) constante\((f=a_{k i})\) on\(A_{k i}, i=1,2, \ldots\). Entonces
\[A=\bigcup_{k} B_{k}=\bigcup_{k} \bigcup_{i} A_{k i}\]
es una\(\mathcal{M}\) partición -de\(A\) en los conjuntos disjuntos\(A_{k i} \in \mathcal{M}\).
Ahora, por definición,
\[\int_{B_{k}} f=\sum_{i} a_{k i} m A_{k i}\]
y
\[\int_{A} f=\sum_{k, i} a_{k i} m A_{k i}=\sum_{k}\left(\sum_{i} a_{k i} m A_{k i}\right)=\sum_{k} \int_{B_{k}} f\]
por reglas para series dobles. Esto prueba la fórmula (2).
(ii) Si\(f\) es elemental e integrable\(B_{k}(k=1, \ldots, n),\) entonces con la misma notación, tenemos
\[\sum_{i}\left|a_{k i}\right| m A_{k i}<\infty\]
(por integrabilidad); por lo tanto
\[\sum_{k=1}^{n} \sum_{i}\left|a_{k i}\right| m A_{k i}<\infty.\]
Esto significa, sin embargo, que\(f\) es elemental e integrable en\(A,\) y así sigue la cláusula (ii). \(\quad \square\)
Precaución. La cláusula (ii) falla si la partición\(\{B_{k}\}\) es infinita.
(i) Si\(f, g : S \rightarrow E^{*}\) son elementales y no negativos en\(A,\) entonces
\[\int_{A}(f+g)=\int_{A} f+\int_{A} g.\]
(ii) Si\(f, g : S \rightarrow E\) son elementales e integrables en\(A,\) lo que es\(f \pm g,\) y
\[\int_{A}(f \pm g)=\int_{A} f \pm \int_{A} g.\]
- Prueba
-
Argumentando como en la prueba del Teorema 1 de §1, podemos hacer\(f\) y\(g\) constantes en conjuntos de uno y el mismo\(\mathcal{M}\) -partición de\(A,\) decir,\(f=a_{i}\) y\(A_{i} \in \mathcal{M};\) así\(g=b_{i}\) sucesivamente
\[f \pm g=a_{i} \pm b_{i} \text { on } A_{i}, \quad i=1,2, \ldots.\]
En el caso (i),\(f, g \geq 0;\) por lo que la integrabilidad es irrelevante por la Nota 3, y la fórmula (1) rinde
\[\int_{A}(f+g)=\sum_{i}\left(a_{i}+b_{i}\right) m A_{i}=\sum_{i} a_{i} m A_{i}+\sum b_{i} m A_{i}=\int_{A} f+\int_{A} g.\]
En (ii), de manera similar obtenemos
\[\sum_{i}\left|a_{i} \pm b_{i}\right| m A_{i} \leq \sum\left|a_{i}\right| m A_{i}+\sum_{i}\left|b_{i}\right| m A_{i}<\infty.\]
(¿Por qué?) Así\(f \pm g\) es elemental e integrable en\(A.\) Como antes, también obtenemos
\[\int_{A}(f \pm g)=\int_{A} f \pm \int_{A} g,\]
simplemente por reglas para la adición de series convergentes. (¡Verifica!) \(\quad \square\)
Nota 4. Como sabemos, se define la función característica\(C_{B}\) de\(B \subseteq S\) un conjunto
\[C_{B}(x)=\left\{\begin{array}{ll}{1,} & {x \in B,} \\ {0,} & {x \in S-B.}\end{array}\right.\]
Si\(g : S \rightarrow E\) es elemental encendido\(A,\) para que
\[g=a_{i} \text { on } A_{i}, 1,2, \ldots,\]
para algunos\(\mathcal{M}\) -partición
\[A=\bigcup A_{i},\]
entonces
\[g=\sum_{i} a_{i} C_{A_{i}} \text { on } A.\]
(Esta suma siempre existe para conjuntos disconjuntos\(A_{i}.\) ¿Por qué?) A menudo utilizaremos esta notación.
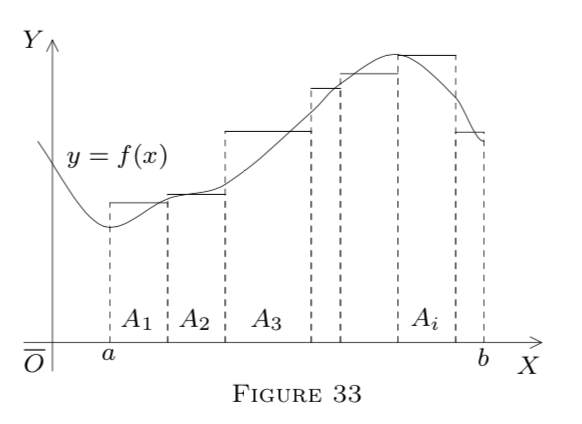
Si\(m\) es Lebesgue medida en\(E^{1},\) la integral
\[\int_{A} g=\sum_{i} a_{i} m A_{i}\]
tiene una interpretación geométrica simple; ver Figura 33. \(A=[a, b] \subset E^{1};\)Dejar\(g\) ser acotado y no negativo en\(E^{1}.\) Cada producto\(a_{i} m A_{i}\) es el área de un rectángulo con base\(A_{i}\) y altitud\(a_{i}.\) (Asumimos\(A_{i}\) que el ser intervalos aquí.) El área total,
\[\int_{A} g=\sum_{i} a_{i} m A_{i},\]
puede tratarse como una aproximación al área bajo alguna curva\(y=f(x)\), donde\(f\) se aproxima por\(g\) (Teorema 3 en §1). Históricamente, la integración surgió de tales aproximaciones.
Integración de funciones elementales ampliadas reales. La nota 3 se puede extender a las funciones de cambio de signo de la siguiente manera.
Si
\[f=\sum_{i} a_{i} C_{A_{i}} \quad\left(a_{i} \in E^{*}\right)\]
en
\[A=\bigcup_{i} A_{i} \quad\left(A_{i} \in \mathcal{M}\right),\]
nosotros fijamos
\[\int_{A} f=\int_{A} f^{+}-\int_{A} f^{-},\]
con
\[f^{+}=f \vee 0 \geq 0 \text { and } f^{-}=(-f) \vee 0 \geq 0;\]
ver §2.
Por Teorema 2 en §2,\(f^{+}\) y\(f^{-}\) son elementales y no negativos por\(A;\) lo
\[\int_{A} f^{+} \text { and } \int_{A} f^{-}\]
están definidos por la Nota 3, y así lo es
\[\int_{A} f=\int_{A} f^{+}-\int_{A} f^{-}\]
por nuestras convenciones (2*) en el Capítulo 4, §4.
Tendremos uso para la fórmula (3), aunque
\[\int_{A} f^{+}=\int_{A} f^{-}=\infty;\]
entonces decimos que\(\int_{A} f\) es poco ortodoxo y lo equiparamos\(+\infty,\) por convención; cf. Capítulo 4, §4. (Otras integrales se llaman ortodoxas.) Así, para las funciones elementales y (extendidas) reales, siempre\(\int_{A} f\) se define. (Desarrollamos aún más esta idea en §5.)
Nota 5. Con\(f\) lo anterior, claramente tenemos
\[f^{+}=a_{i}^{+} \text { and } f^{-}=a_{i}^{-} \text { on } A_{i},\]
donde
\[a_{i}^{+}=\max \left(a_{i}, 0\right) \text { and } a_{i}^{-}=\max \left(-a_{i}, 0\right).\]
Por lo tanto
\[\int_{A} f^{+}=\sum a_{i}^{+} \cdot m A_{i} \text { and } \int_{A} f^{-}=\sum a_{i}^{-} \cdot m A_{i},\]
para que
\[\int_{A} f=\int_{A} f^{+}-\int_{A} f^{-}=\sum_{i} a_{i}^{+} \cdot m A_{i}-\sum_{i} a_{i}^{-} \cdot m A_{i}.\]
Si\(\int_{A} f^{+}<\infty\) o\(\int_{A} f^{-}<\infty,\) podemos restar las dos series a términos (Problema 14 del Capítulo 4, §13) para obtener
\[\int_{A} f=\sum_{i}\left(a_{i}^{+}-a_{i}^{-}\right) m A_{i}=\sum_{i} a_{i} m A_{i}\]
para\(a_{i}^{+}-a_{i}^{-}=a_{i}.\) Así las fórmulas (3) y (4) concuerdan con nuestras definiciones anteriores.


