2.7: Segunda Derivada y Concavidad
- Page ID
- 110605
Segunda Derivada y Concavidad
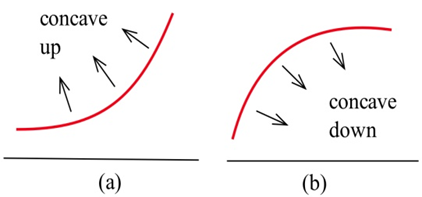
Gráficamente, una función es cóncava hacia arriba si su gráfica está curvada con la abertura hacia arriba (Figura\(\PageIndex{1a}\)). De igual manera, una función es cóncava hacia abajo si su gráfica se abre hacia abajo (Figura\(\PageIndex{1b}\)).
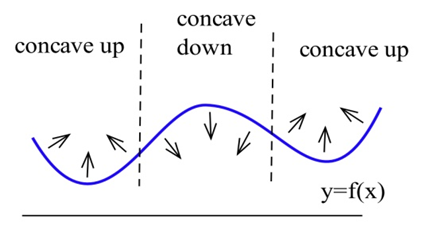
Esta figura muestra la concavidad de una función en varios puntos. Observe que una función puede ser cóncava hacia arriba independientemente de si está aumentando o disminuyendo.
Por ejemplo, una epidemia: Supongamos que una epidemia ha comenzado, y usted, como miembro del congreso, debe decidir si los métodos actuales están combatiendo efectivamente la propagación de la enfermedad o si se necesitan medidas más drásticas y más dinero. En la Figura\(\PageIndex{2}\) a continuación,\(f(x)\) se muestra el número de personas que tienen la enfermedad en el momento\(x\), y se muestran dos situaciones diferentes. Tanto en Figura\(\PageIndex{2a}\) como en Figura\(\PageIndex{2b}\), el número de personas con la enfermedad\(f(\text{now})\), y la tasa a la que las nuevas personas se enferman,\(f'(\text{now})\), son las mismas. La diferencia en las dos situaciones es la concavidad de\(f\), y esa diferencia en la concavidad podría tener un gran efecto en tu decisión.
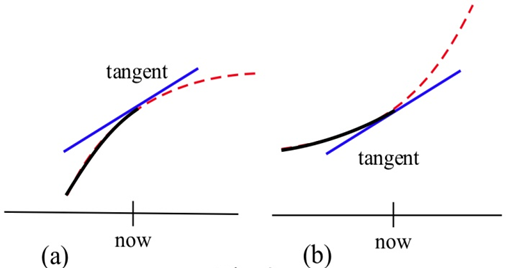
En Figura\(\PageIndex{2a}\),\(f\) es cóncava hacia abajo en “ahora”, las pendientes están disminuyendo, y parece como si se estuviera despegando. Podemos decir "\(f\)está aumentando a un ritmo decreciente”. Parece que los métodos actuales están empezando a controlar la epidemia.
En Figura\(\PageIndex{2b}\),\(f\) es cóncava hacia arriba, las pendientes van en aumento, y parece que seguirá aumentando cada vez más rápido. Parece que la epidemia aún está fuera de control.
Las diferencias entre las gráficas provienen de si la derivada está aumentando o disminuyendo
La derivada de una función\(f\) es una función que da información sobre la pendiente de\(f\). La derivada nos dice si la función original está aumentando o disminuyendo.
Porque\(f'\) es una función, podemos tomar su derivada. Esta segunda derivada también nos da información sobre nuestra función original\(f\). La segunda derivada nos da una forma matemática de decir cómo se curva la gráfica de una función. La segunda derivada nos dice si la función original es cóncava hacia arriba o hacia abajo.
Dejar que la\( y=f(x) \). The segunda derivada de\(f\) es la derivada de\( y'=f'(x) \).
Usando notación prima, esto es\( f''(x) \) o\( y'' \). Puedes leer esto en voz alta como "\(f\)doble primo de\(x\)" o "\(y\)doble primo”.
Usando la notación Leibniz, la segunda derivada se escribe\( \frac{d^2y}{dx^2} \) o\( \frac{d^2f}{dx^2} \). Esto se lee en voz alta como “la segunda derivada de\(y\) (o\(f\))”.
La primera derivada nos dice si una función está aumentando o disminuyendo
Si\( f'(x) \) es positivo en un intervalo, la gráfica de\( y=f(x) \) va en aumento en ese intervalo.
Si\( f'(x) \) es negativo en un intervalo, la gráfica de\( y=f(x) \) está disminuyendo en ese intervalo.
La segunda derivada nos dice si una función es cóncava hacia arriba o cóncava hacia abajo
Si\( f''(x) \) es positivo en un intervalo, la gráfica de\( y=f(x) \) es cóncava hacia arriba en ese intervalo. Podemos decir que\(f\) está aumentando (o disminuyendo) a un ritmo creciente.
Si\( f''(x) \) es negativo en un intervalo, la gráfica de\( y=f(x) \) es cóncava hacia abajo en ese intervalo. Podemos decir que\(f\) está aumentando (o disminuyendo) a un ritmo decreciente.
Encuentra\( f''(x) \) para\( f(x)=3x^7 \).
Primero, necesitamos encontrar la primera derivada:\[f'(x)=21x^6.\nonumber \]
Luego tomamos la derivada de esa función:\[f''(x)=\frac{d}{dx}\left( f'(x) \right)=\frac{d}{dx}\left( 21x^6 \right)=126x^5. \nonumber \]
Si\(f(x)\) representa la posición de una partícula en el tiempo\(x\), entonces\(v(x) = f '(x)\) representará la velocidad (tasa de cambio de la posición) de la partícula y\(a(x) = v '(x) = f ''(x)\) representará la aceleración (la velocidad de cambio de la velocidad) de la partícula.
Probablemente esté familiarizado con la aceleración de conducir o conducir en un automóvil. El velocímetro te indica tu velocidad (velocidad). Cuando sales de una parada y presionas hacia abajo el acelerador, estás acelerando, aumentando tu velocidad.
La altura (pies) de una partícula en el tiempo\(t\) segundos es\(f(t) = t^3 – 4t^2 + 8t\). Encuentra la altura, velocidad y aceleración de la partícula cuando\(t =\) 0, 1 y 2 segundos.
\(f(t) = t^3 – 4t^2 + 8t\)así\(f(0) = 0\) pies,\(f(1) = 5\) pies y\(f(2) = 8\) pies.
La velocidad es\(v(t) = f '(t) = 3t^2 – 8t + 8\) tan\( v(0) = 8\) pies/s,\(v(1) = 3\) pies/s y\(v(2) = 4\) pies/s. En cada uno de estos tiempos la velocidad es positiva y la partícula se mueve hacia arriba, aumentando en altura.
La aceleración es\(a(t) = f ''(t) = 6t – 8\) así\(a(0) = –8 \text{ ft/s\(^2\)}\),\(a(1) = –2 \text{ ft/s\(^2\)}\) y\(a(2) = 4 \text{ ft/s\(^2\)}\).
En los tiempos 0 y 1, la aceleración es negativa, por lo que la velocidad de la partícula estaría disminuyendo en esos puntos; la partícula se estaba desacelerando. En el tiempo 2, la velocidad es positiva, por lo que la partícula estaba aumentando en velocidad.
Puntos de Inflexión
Un punto de inflexión es un punto en la gráfica de una función donde la concavidad de la función cambia, de cóncava hacia abajo o de cóncava de abajo a arriba.
¿Cuáles de los puntos etiquetados en la gráfica a continuación son puntos de inflexión?
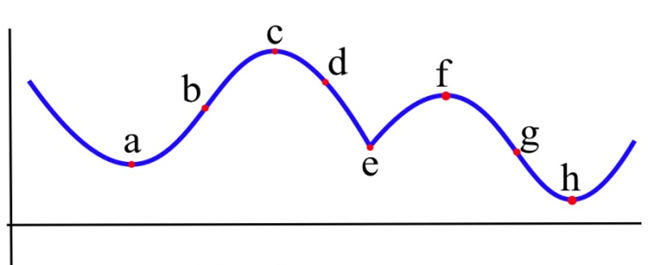
La concavidad cambia en los puntos b y g. En los puntos a y h, la gráfica es cóncava hacia arriba en ambos lados, por lo que la concavidad no cambia. En los puntos c y f, la gráfica es cóncava hacia abajo en ambos lados. En el punto e, aunque la gráfica se vea extraña ahí, la gráfica es cóncava hacia abajo en ambos lados — la concavidad no cambia.
Los puntos de inflexión ocurren cuando la concavidad cambia. Debido a que conocemos la conexión entre la concavidad de una función y el signo de su segunda derivada, podemos usar esto para encontrar puntos de inflexión.
Un punto de inflexión es un punto en la gráfica donde la segunda derivada cambia de signo.
Para que la segunda derivada cambie los signos, debe ser cero o estar indefinida. Entonces, para encontrar los puntos de inflexión de una función solo necesitamos verificar los puntos donde\(f ''(x)\) está 0 o indefinido.
Tenga en cuenta que no es suficiente que la segunda derivada sea cero o indefinida. Todavía tenemos que verificar que el signo de\( f'' \) cambios firme. Las funciones del siguiente ejemplo ilustran lo que puede suceder.
Vamos\(f(x) = x^3\),\(g(x) = x^4\) y\(h(x) = x^{1/3}\). ¿Para cuál de estas funciones es el punto (0,0) un punto de inflexión?
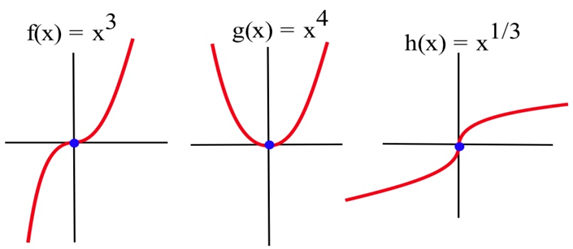
Gráficamente, es claro que la concavidad de\(f(x) = x^3\) y\(h(x) = x^{1/3}\) cambia en (0,0), por lo que (0,0) es un punto de inflexión para\(f\) y\(h\). La función\(g(x) = x^4\) es cóncava en todas partes por lo que (0,0) no es un punto de inflexión de\(g\).
También podemos calcular las segundas derivadas y verificar el cambio de signo.
Si\(f(x) = x^3\), entonces\(f'(x) = 3x^2\) y\( f''(x) = 6x\). El único punto en el que\(f''(x) = 0\) o es indefinido (no\(f'\) es diferenciable) está en\(x = 0\). Si\( x \lt 0\), entonces\(f ''(x) \lt 0\) así\(f\) es cóncavo hacia abajo. Si\(x \gt 0\), entonces\(f''(x) \gt 0\) así\(f\) es cóncavo hacia arriba. En\(x = 0\) la concavidad cambia por lo que el punto\((0,f(0)) = (0,0)\) es un punto de inflexión de\(f(x)=x^3\).
Si\(g(x) = x^4\), entonces\(g'(x) = 4x^3\) y\(g''(x) = 12x^2\). El único punto en el que\(g''(x) = 0\) o es indefinido es en\(x = 0\). Si\(x \lt 0\), entonces\(g''(x) \gt 0\) así\(g\) es cóncavo hacia arriba. Si\(x \gt 0\),\(g ''(x) \gt 0\) entonces también\(g\) es cóncavo hacia arriba. En\(x = 0\) la concavidad no cambia por lo que el punto no\((0, g(0)) = (0,0)\) es un punto de inflexión de\(g(x)=x^4\). ¡Ten en cuenta este ejemplo!
Si\(h(x) = x^{1/3}\), entonces\(h'(x) = \frac{1}{3}x^{-2/3}\) y\(h''(x) = -\frac{2}{9}x^{-5/3}\). \(h''\)no se define si\(x = 0\), pero\(h''(\text{negative number}) \gt 0\) y\(h''(\text{positive number}) \lt 0\) así\(h\) cambia la concavidad en (0,0) y (0,0) es un punto de inflexión de\(h\).
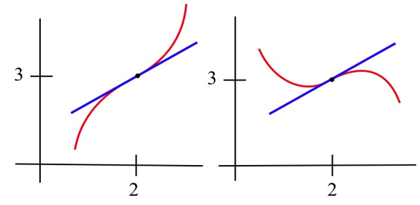
Esboce la gráfica de una función con\(f(2) = 3\)\(f '(2) = 1\), y un punto de inflexión en (2,3).
Aquí se muestran dos posibles soluciones.