3.8: Aplicaciones a los Negocios

Excedente de consumo y productor

Aquí hay una curva de demanda y oferta para un producto. ¿Cuál es cuál?

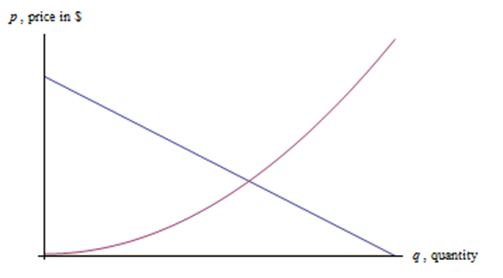
La curva de demanda está disminuyendo: los precios más bajos se asocian con mayores cantidades demandadas, los precios más altos se asocian con menores cantidades demandadas. Las curvas de demanda a menudo se muestran como si fueran lineales, pero no hay razón por la que tengan que serlo.

La curva de oferta va en aumento: los precios más bajos se asocian con una menor oferta, y los precios más altos se asocian con mayores cantidades suministradas.

El punto donde se cruzan la curva de demanda y oferta se denomina punto de equilibrio\((q^*, p^*)\).

Supongamos que el precio se fija en el precio de equilibrio, de manera que la cantidad demandada sea igual a la cantidad suministrada. Ahora piensa en la gente que está representada a la izquierda del punto de equilibrio. Los consumidores de la izquierda habrían estado dispuestos a pagar un precio superior al que terminaron teniendo que pagar, por lo que el precio de equilibrio les ahorró dinero. Por otro lado, los productores representados por la izquierda habrían estado dispuestos a abastecer estos bienes por un precio más bajo —ganaron más dinero del que esperaban. ¡Ambos grupos terminaron con dinero extra en sus bolsillos!

Gráficamente, la cantidad de dinero extra que terminó en los bolsillos de los consumidores es el área entre la curva de demanda y la línea horizontal en\(p^*\). Esta es la diferencia de precio, resumida sobre todos los consumidores que gastaron menos de lo que esperaban, una integral definitiva. Observe que dado que el área debajo de la línea horizontal es un rectángulo, podemos simplificar la integral del área:\[ \int\limits_0^{q^*} \left( d(q)-p^*\right)\, dq = \int\limits_0^{q^*} d(q)\, dq - \int\limits_0^{q^*} p^*\, dq = \int\limits_0^{q^*} d(q)\, dq - p^*q^*.\nonumber \]

La cantidad de dinero extra que terminó en los bolsillos de los productores es el área entre la curva de oferta y la línea horizontal en\(p^*\). Esta es la diferencia de precio, resumida sobre todos los productores que recibieron más de lo que esperaban. Similar al excedente del consumidor, esta integral puede simplificarse:\[ \int\limits_0^{q^*} \left( p^*-s(q) \right)\, dq = \int\limits_0^{q^*} p^*\, dq - \int\limits_0^{q^*} s(q)\, dq = p^*q^* - \int\limits_0^{q^*} s(q)\, dq.\nonumber \]

Excedente de consumo y productor

Dada una función de demanda\(p = d(q)\) y una función de oferta\(p = s(q)\), y el punto de equilibrio\((q^*, p^*)\)

• El excedente del consumidor es\[\int\limits_0^{q^*} d(q)\, dq - p^*q^*.\nonumber \]
• El excedente del productor es\[p^*q^* - \int\limits_0^{q^*} s(q)\, dq.\nonumber \]
• La suma del superávit del consumidor y del superávit del productor son las ganancias totales del comercio.

¿Cuáles son las unidades de excedente de consumidor y productor? Las unidades son (precio por artículo) (cantidad de artículos) = ¡dinero!

Ejemplo\(\PageIndex{1}\)

Supongamos que la demanda de un producto viene dada por\( p=d(q)=-0.8q+150 \) y la oferta para el mismo producto viene dada por\( p=s(q)=5.2q \). Para ambas funciones,\(q\) es la cantidad y\(p\) es el precio, en dólares.

1. Encuentra el punto de equilibrio.
2. Encuentre el excedente del consumidor al precio de equilibrio.
3. Encuentre el excedente del productor al precio de equilibrio.

Solución

1. El punto de equilibrio es donde las funciones de oferta y demanda son iguales. \[ \begin{align*} -0.8q+150 & = 5.2q \\ 150 & = 6.0q \\ q & = \frac{150}{6} \\ q & = 25 \end{align*} \nonumber \]

   La cantidad de equilibrio es de 25 ítems. Para encontrar el precio de equilibrio correspondiente podemos usar ya sea la ecuación de demanda o oferta.

   \(s(25) = 5.2(25) = 130\). El precio de equilibrio es de 130 dólares.

2. El excedente del consumidor es\[ \begin{align*} \int_0^{25} (-0.8q+150)\, dq - (130)(25) & = \left[-0.8 \frac{q^2}{2} + 150 q\right]_0^{25} - 3250 \\ & = \left(-0.4\left(25^2\right) + 150(25)\right) - \left(-0.4\left(0^2\right) + 150(0)\right) - 3250 \\ & = 3500 - 0 - 3250 \\ & = \$250 \end{align*} \nonumber \]
3. El excedente del productor es\[ \begin{align*} (130)(25) - \int_0^{25} 5.2q\, dq & = 3250 - \left[5.2 \frac{q^2}{2}\right]_0^{25} \\ & = 3250 - \left(\left(2.6\left(25^2\right)\right) - \left(2.6\left(0^2\right)\right)\right) \\ & = 3250 - (1625 - 0) \\ & = \$1625 \end{align*} \nonumber \]

Ejemplo\(\PageIndex{2}\)

Supongamos que la demanda de un producto viene dada por\( p=d(q)=300-5q \) y la oferta para el mismo producto viene dada por\( p=s(q)=q^2 \). Para ambas funciones,\(q\) es la cantidad y\(p\) es el precio, en dólares.

1. Encuentra el punto de equilibrio.
2. Encuentre el excedente del consumidor al precio de equilibrio.
3. Encuentre el excedente del productor al precio de equilibrio.

Solución

1. Esto es cuadrático, así podemos reorganizar la ecuación para que un lado sea cero:\(q^2 + 5q - 300 = 0\).

   Podríamos resolver esto usando la ecuación cuadrática:\(q = \frac{-5 \pm \sqrt{5^2-4(1)(-300)}}{2(1)}\)

   o podríamos factorial:\((q+20)(q-15)=0\), así\(q =-20\) o\(q = 15\).

   Queremos la solución positiva. La cantidad de equilibrio es de 15 ítems. El precio de equilibrio es\(s(15) = 15^2 = \$225\).

2. El excedente del consumidor es\[ \begin{align*} \int_0^{15} (300-5q)\, dq - (225)(15) & = \left[300q - 5\frac{q^2}{2}\right]_0^{15} - 3375 \\ & = \left(300(15) - 2.5\left(15^2\right)\right) - \left(300(0) - 2.5\left(0^2\right)\right) - 3375 \\ & = 3937.5 - 0 - 3375 \\ & = \$562.50 \end{align*} \nonumber \]
3. El excedente del productor es\[ \begin{align*} (225)(15) - \int_0^{15} q^2\, dq & = 3375 - \left[\frac{q^3}{3}\right]_0^{15}s \\ & = 3375 - \left(\left(\frac{15^3}{3}\right) - \left(\frac{0^3}{3}\right)\right) \\ & = 3375 - (1125 - 0) \\ & = \$2250 \end{align*} \nonumber \]

Ejemplo\(\PageIndex{3}\)

Las tablas siguientes muestran información sobre las funciones de demanda y oferta de un producto. Para ambas funciones,\(q\) es la cantidad y\(p\) es el precio, en dólares.

q	0	100	200	300	400	500	600	700
p	70	61	53	46	40	35	31	28

q	0	100	200	300	400	500	600	700
p	14	21	28	33	40	47	54	61

1. ¿Cuál es cuál? Es decir, ¿qué tabla representa la demanda y cuál representa la oferta?
2. ¿Cuál es el precio y la cantidad de equilibrio?
3. Encuentre el excedente de consumidor y productor al precio de equilibrio.

Solución

1. La primera tabla muestra el precio decreciente asociado al aumento de la cantidad; es decir, la función de demanda.
2. Para ambas funciones,\(q = 400\) se asocia con\(p = 40\); el precio de equilibrio es de $40 y la cantidad de equilibrio es de 400 unidades. Observe que aquí tuvimos suerte, porque el punto de equilibrio es en realidad uno de los puntos mostrados. En muchos casos con una tabla, tendríamos que estimar.
3. El excedente del consumidor utiliza la función de demanda, que proviene de la primera tabla. Tendremos que aproximar el valor de la integral usando rectángulos. Hay 4 rectángulos, y vamos a elegir usar los extremos izquierdos.

   El excedente del consumidor es\[ \begin{align*} \int\limits_0^{400} \text{(demand)}\, dq-(40)(400)\approx & \\ (100)(70+61+53+46)-(40)(400) & = \$7000 \end{align*} \nonumber \] Así que el excedente del consumidor es de alrededor de $7000

   El excedente productor utiliza la función de oferta, que proviene de la segunda tabla. Optemos por usar los endpoints izquierdos para esta integral también.

   El excedente productor es\[ \begin{align*} (40)(400)-\int\limits_0^{400} \text{(supply)}\, dq \approx & \\ (40)(400)-(100)(14+21+28+33) & = \$6400 \end{align*} \nonumber \] Así que el excedente del productor es de unos 6400 dólares.

Corriente Continua de Ingresos

En el precálculo, aprendiste sobre el interés compuesto en esa situación realmente simple en la que hiciste un solo depósito en una cuenta que devengo intereses y la dejaste reposar sin ser molestado, ganando intereses, durante algún período de tiempo. Recordar:

Fórmulas de interés compuesto

Dejar\(P\) ser el principal (inversión inicial),\(r\) ser la tasa de interés anual expresada en decimal, y\(A(t)\) ser la cantidad en la cuenta al final de los\(t\) años.

\(n\)Tiempos de composición por año

\[ A(t) = P\left(1+\frac{r}{n}\right)^{nt} \nonumber \]

Compuesto continuamente

\[ A(t)=Pe^{rt} \nonumber \]

Si estás usando esta fórmula para encontrar lo que valdrá una cuenta en el futuro,\(t \gt 0\) y\(A(t)\) se llama el valor futuro.

Si estás usando la fórmula para encontrar lo que necesitas depositar hoy para tener un cierto valor en\(P\) algún momento en el futuro,\(t \lt 0\) y\(A(t)\) se llama el valor presente.

También es posible que hayas aprendido fórmulas de anualidades algo más complicadas para hacer frente a situaciones un poco más complicadas, en las que haces depósitos iguales a la misma distancia en el tiempo.

Pero la vida real no suele ser tan ordenada.

El cálculo nos permite manejar situaciones en las que los depósitos fluyen continuamente hacia una cuenta que gana intereses. Siempre y cuando podamos modelar el flujo de ingresos con una función, podemos usar una integral definida para calcular el valor presente y futuro de un flujo de ingresos continuo. La idea aquí es que cada pedacito de ingreso en el futuro necesita ser multiplicado por la función exponencial para traerlo de vuelta al presente, y luego los sumaremos todos (una integral definitiva).

Flujo de Ingresos Continuos

Supongamos que el dinero puede ganar intereses a una tasa de interés anual de\(r\), compounded continuously. Let \(F(t)\) be a continuous income function (in dollars per year) that applies between year 0 and year \(T\).

Entonces el valor presente de ese flujo de ingresos viene dado por\[ PV = \int\limits_0^T F(t)e^{-rt}\, dt. \nonumber \]

El valor futuro puede calcularse mediante la fórmula de interés compuesto ordinario\[ FV = PVe^{rt}. \nonumber \]

Esta es una manera útil de comparar dos inversiones —encontrar el valor actual de cada una para ver cuál vale más hoy en día.

Ejemplo\(\PageIndex{4}\)

Tienes la oportunidad de comprar un negocio que ganará $75,000 anuales continuamente durante los próximos ocho años. El dinero puede ganar 2.8% anual, agravado continuamente. ¿Este negocio vale su precio de compra de $630,000?

Solución

Primero, tenga en cuenta que todavía tenemos que hacer algunas suposiciones simplificadoras. Tenemos que suponer que las tasas de interés van a permanecer constantes durante esos ocho años enteros. También tenemos que asumir que los $75,000 anuales están llegando continuamente, como un grifo que gotea dólares en el negocio. Ninguno de estos supuestos podría ser exacto.

Pero para seguir adelante: El valor actual de los 630.000 dólares es, bueno, 630.000 dólares. Esta es una inversión, donde ponemos nuestros $630,000 en el banco y lo dejamos sentar ahí.

Para encontrar el valor actual del negocio, lo consideramos como un flujo de ingresos. La función\(F(t)\) en este caso es una constante de $75,000 dólares al año, entonces\(F(t) = 75,\!000\). La tasa de interés es de 2.8% y el plazo que nos interesa es de 8 años, así\(r = .028\), y\(T = 8\):\[ PV=\int\limits_0^8 75000e^{-0.028t}\, dt \approx 537,\!548.75 \nonumber \]

El valor actual del negocio es de alrededor de $537,500, que es menor que el precio de venta de 630.000 dólares, por lo que este no es un buen trato.

Si bien esta integral podría haberse hecho usando sustitución, para muchas de las integrales de esta sección no tenemos las técnicas para usar antiderivados o, en algunos casos, no existe ningún antiderivado. La tecnología funcionará rápidamente, y te dará una respuesta que es lo suficientemente buena.

Ejemplo\(\PageIndex{5}\)

Una empresa está considerando comprar una nueva máquina para su piso de producción. La máquina cuesta $65,000. La compañía estima que los ingresos adicionales de la máquina serán de $7000 constantes para el primer año, luego aumentarán en $800 cada año después de eso. Para poder comprar la máquina, la empresa necesita estar convencida de que se pagará por sí misma a finales de 8 años con este ingreso adicional. El dinero puede ganar 1.7% anual, agravado continuamente. ¿Debería la empresa comprar la máquina?

Solución

Asumiremos que los ingresos llegarán continuamente a lo largo de los 8 años. También asumiremos que las tasas de interés permanecerán constantes durante ese período de 8 años.

Nos interesa el valor actual de la máquina, que compararemos con su etiqueta de precio de 65,000 dólares. \(t\)Sea el tiempo, en años, desde la compra de la máquina. El ingreso de la máquina es diferente dependiendo del tiempo.

De\(t = 0\) a\(t = 1\) (el primer año), el ingreso es constante $7000 por año. De\(t = 1\) a\(t = 8\), los ingresos aumentan en $800 cada año; la función de flujo de ingresos\(F(t)\) será\( F(t)=7000+800(t-1)=6200+800t \). Para encontrar el valor actual, tendremos que dividir la integral en las dos piezas, una para cada una de las funciones:\[ PV=\int\limits_0^1 7000e^{-0.017t}\, dt + \int\limits_1^8 (6200+800t)e^{-0.017t}\, dt \approx 70166. \nonumber \]

El valor actual es mayor que el costo de la máquina, por lo que la empresa debe comprar la máquina.