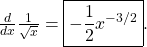3.2: Regla de poder

“¡Tengo el poder!” —Snap (banda alemana)

Si aplicas la definición de la derivada a varias funciones, verás:

\(\begin{array}{cc} \frac{d}{dx} x^0 & 0 \\ \frac{d}{dx} x^1 & 1\\ \frac{d}{dx} x^2 & 2x \\ \frac{d}{dx} x^3 & 3x^2 \\ \frac{d}{dx} x^4 & 4x^3 \end{array}\)

¿Ves el patrón?

\(\boxed{\frac{d}{dx} x^n = n x^{n-1}}\)

Como veremos en la siguiente sección, esto incluso funciona para los no enteros. La clave es multiplicar por el exponente, luego disminuir el exponente por uno.

Las siguientes reglas dicen que los múltiplos constantes y la suma funcionan muy bien.

\(\boxed{\frac{d}{dx} c \cdot f(x) = c f'(x)}\)

\(\boxed{\frac{d}{dx} [f(x) + g(x)] = f'(x) + g'(x)}\)

La clave es que solo puedes preocuparte por la derivada de cada pieza de una suma por separado. Multiplos constantes “vienen para el paseo”. Con sólo estas tres reglas, ahora se puede tomar la derivada de cualquier polinomio. Compruébalo.

Poder

Encuentra las siguientes derivadas.

1. \(\frac{d}{dx} 3x^2\)

   Para hacer esto, usamos la regla de poder por\(x^2\) parte, y obtenemos\(2x\). No obstante, también estamos multiplicando por\(3\), por lo que la respuesta también\(3\) se multiplica por. De ahí que la respuesta sea\(3(2x) = \boxed{6x}\).

2. \(\frac{d}{dx} x^3 + x\)

   Por la regla del poder, encontramos\(\frac{d}{dx} x^3 = 3x^2\), y\(\frac{d}{dx} x\) es\(\frac{d}{dx} x^1\) que se convierte\(1x^0\) por la regla del poder, que es\(1\). Por la regla de adición, tenemos\(\frac{d}{dx} x^3 + x = \boxed{3x^2 + 1}\).

3. \(\frac{d}{dx} 2x^3 + 5\)

   Tomas el derivado de\(x^3\) y tienes\(3x^2\). Veces por\(2\), eso deja\(6x^2\). Bien, ¿sobre los cinco? Es tentador dejar los cinco puestos, pero en realidad\(\frac{d}{dx} 5 = 0\). ¿Por qué? Bueno, es una constante, por lo que no afecta la pendiente. De ahí que obtengamos\(\boxed{6x^2}\).

Más ejemplos de reglas de poder

¡Tenga en cuenta que la regla de potencia también funciona con exponentes fraccionarios y negativos! Aquí hay algunos ejemplos.

Fraccional

Encuentra.

Para aplicar la regla de poder en este caso, primero necesitamos multiplicar por el exponente (), luego restar uno del exponente. Entonces tenemos

Negativo

Encuentra\(\frac{d}{dx} 7x^{-2}\).

En este problema, solo nos preocupamos por el\(x^{-2}\) para empezar. Multiplicamos por el exponente\(({\color{red} -2})\), y luego restamos uno de eso para obtener\({\color{blue} -2 - 1 = -3}\). Entonces tenemos

\(\frac{d}{dx} 7x^{-2} = 7 ({\color{red} -2} x^

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Matematicas/Calculo_informal_con_aplicaciones_a_las_ciencias_biologicas_y_ambientales_(Seacrest)/03:_Reglas_para_Derivados/3.02:_Regla_de_poder), /content/body/div[2]/div[2]/div/p[3]/span/span, line 1, column 1

) = \boxed{-14 x^{-3}}\)

A veces hay exponentes fraccionarios o negativos ocultos. No dejes que te engañen, son como los ejemplos anteriores. Solo recuerda estas reglas:

\(\boxed{\frac{1}{x^n} = x^{-n}}\)

Veamos algunos ejemplos.

Raíces

Encuentra

1. \(\frac{d}{dx} \sqrt{x}\)

   Este problema es mucho más fácil si podemos reescribir el\(\sqrt{x}\). Esto es lo mismo que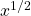, y de ahí tenemos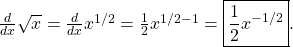

   

2. \(\frac{d}{dx} 5\sqrt[3]{x}\)

   Para resolver esto, realmente ayuda reescribir\(\sqrt[3]{x}\) como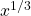. Una vez que haces eso, este prolem es solo la regla de poder y la regla múltiple constante: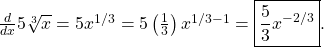

   

3. \(\frac{d}{dx} \sqrt[5]{x^3} + x^2 + 7\)

   Enfócate primero en las partes fáciles: lo sabemos\(\frac{d}{dx} x^2 = 2x\), y lo sabemos\(\frac{d}{dx} 7 = 0\). Así que sólo tenemos que averiguar el\(\frac{d}{dx} \sqrt[5]{x^3}\). ¿Qué es esto? Bueno, podemos reescribir esto como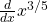. Entonces ahora es solo la regla del poder, y multiplicamos por 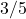y restamos para obtener. De ahí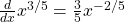. Poniéndolo todo junto:

   

Poderes de\(x\) in the denominator

1. \(\frac{d}{dx} \frac{1}{x}\)

   Podemos reescribir\(\frac{d}{dx} \frac{1}{x} = \frac{d}{dx} \frac{1}{x^1}\) como\(\frac{d}{dx} x^{-1}\). Ahora aplicamos la regla de poder:

   \(\frac{d}{dx} \frac{1}{x} = \frac{d}{dx} x^{-1} = \boxed{-1 x^{-2}}.\)

2. \(\frac{d}{dx} \frac{4}{x^2}\)

   Podemos pensar que es solo una constante al frente, y por lo tanto queremos\(\frac{d}{dx} 4 \left( \frac{1}{x^2} \right )\).\(4\) Entonces podemos reescribir\(\frac{1}{x^2}\) como\(x^{-2}\). Y queremos\(\frac{d}{dx} 4(x^{-2})\). Usando la regla de poder, multiplicamos por\(-2\) y restamos uno, y tenemos

   \(\frac{d}{dx} \frac{4}{x^2} = \frac{d}{dx} 4x^{-2} = \boxed{-8 x^{-3}}.\)

3. \(\frac{d}{dx} \frac{1}{\sqrt{x}}\)

   Esto combina lo fraccionario y denominador. Primero reescribimos\(\sqrt{x}\) como:

   

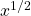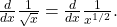
   Luego reescribimos como exponente fraccional negativo.

   

   Por último, utilizamos la regla del poder.