4.4: Tareas- Segundas Derivadas e Interpretación de la Derivada

Última actualización
Guardar como PDF

Page ID: 116627

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Dado cada uno\(f(t)\), describir en una oración el significado de\(f'(t)\).
1. \(f(t)\)Sea la distancia (en millas) que un astronauta está desde la superficie de la tierra mientras estalla hacia el espacio. Aquí\(t\) se mide en horas.
  \(f'(t)\)es la velocidad del astronauta en millas por hora
  ans
2. Dejar\(f(t)\) ser el número de galones de gasolina diesel en el tanque de un camión, con\(t\) medido en horas.
  \(f'(t)\)es lo rápido que se está quemando combustible, en galones por minuto. También podría representar qué tan rápido se está llenando el combustible en una gasolinera.
  ans
3. Dejar\(f(t)\) ser la concentración de NaCl en partes por millón dentro del citoplasma de una célula. Aquí,\(t\) se mide en minutos.
  \(f'(t)\)es la velocidad a la que aumenta la concentración de NaCl en partes por millón por minuto.
  ans
4. Dejar\(f(t)\) ser la velocidad de un corredor (en pies por segundo), y dejar que\(t\) se mida en segundos.
  \(f'(t)\)es la aceleración del corredor, o la velocidad a la que la velocidad del corredor aumenta en (pies por segundo) por segundo.
  ans
5. Deja\(f(t)\) ser la tasa (en dólares por hora) que te pagan, donde\(t\) se mide en meses.
  \(f'(t)\)es como qué tan rápido estás recibiendo aumentos, medidos en (dólares por hora) al mes.
  ans
Para cada una de las funciones siguientes, compute la derivada dos veces. Es decir, computar\(f'(t)\), luego tomar la derivada de\(f'(t)\) para encontrar\(f''(t)\).
1. \(f(t) = 5t^2 - 6t + 2\)
  \(10t - 6\),\(10\)
  ans
2. \(f(t) = t^3 + e^t - \sqrt{t}\).
  ,
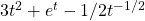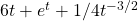  ans
3. \(f(t) = \frac{1}{t}\)
  \(-t^{-2}, 2 t^{-3}\)
  ans
4. \(f(t) = \sin(t)\)
  \(\cos(t)\),\((-\sin(t))\)
  ans
5. \(f(t) = (\sqrt{t} + 1)^2\)
  ,
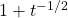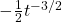  ans
Para cada gráfica, circule cualquier punto de inflexión (si los hubiera). Marcar cada región entre los puntos de inflexión que tiene teniendo una segunda derivada positiva o negativa.
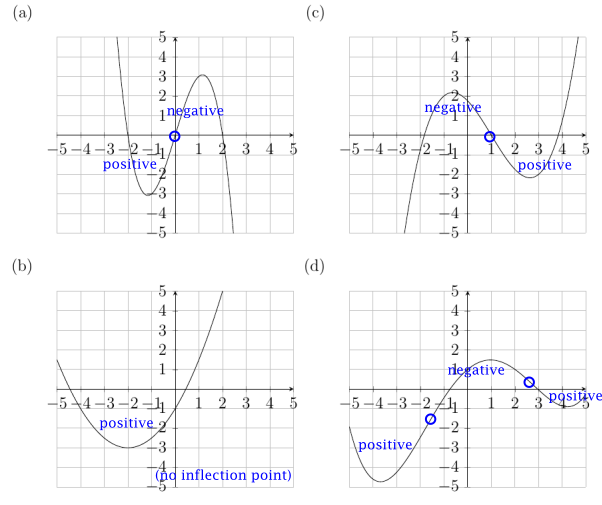ans
Una orilla del río se está erosionando. \(f(t)\)Dejen ser las toneladas métricas de suelo y material rocoso en el día\(t\). Supongamos\(f(t) = 0.05t^2 - 3t + 125\) (este modelo es válido desde\(t = 0\) hasta\(t =30\)).
1. ¿Qué es\(f'(t)\) la medición? ¿Cuáles son las unidades correctas?
  Qué tan rápido se están perdiendo suelo y roca debido a la erosión en toneladas métricas por día.
  ans
2. Esbozar la derivada.
3. Encuentra el derivado
  \(0.1x - 3\)
  ans
4. ¿Qué tan rápido se pierde el material en el día\(t = 5\)? ¿Qué tan rápido se pierde el material en el día\(t = 25\)?
  \(2.5\)toneladas métricas por día en día\(5\), toneladas\(0.5\) métricas por día en día\(25\).
  ans
El precio de las acciones de Math Nerds, Inc, en el transcurso de un día de negociación de 8 horas (\(t = 0\)a\(t = 8\)) se modela por\(p(t) = -0.3t^3 + 3t^2 - 4t + 17\) (\(p(t)\)se mide en dólares).
1. ¿Qué es\(p'(t)\) la medición? ¿Qué es\(p''(t)\) la medición? Indicar las unidades correctas para cada una.
  \(p'(t)\)es la tasa de cambio del precio de las acciones en dólares por hora. \(p''(t)\)es la rapidez con la que el precio de las acciones se está acelerando o desacelerando, medido en dólares por hora\(^2\)
  ans
2. Esbozar la gráfica de\(p'(t)\) y\(p''(t))\).
3. Cómputos\(p'(t)\) y\(p''(t)\).
  \(p'(t) = -0.9t^2 + 6t - 4\),\(p''(t) = -1.8t + 6\).
  ans
4. ¿Qué tan rápido gana el precio de las acciones\(t = 4\)? ¿Qué tan rápido está perdiendo valor en\(t = 7\)?
  Ganando a 5.6 dólares por hora en\(t = 4\), pero perdiendo a una tasa de\(-6.1\) dólares por hora en\(t = 7\)
  ans
5. En\(t = 4\), el precio de las acciones está creciendo claramente. Pero, ¿el crecimiento se está acelerando o desacelerando? ¿Cómo puedes usar la fórmula para\(p(t)\)\(p'(t)\), o\(p''(t)\) para averiguarlo?
  Podemos\(t = 4\) conectarnos\(p''(t)\), para obtener una respuesta de\(-1.2\) dólares por hora por hora, lo que significa que el crecimiento se está desacelerando.
  ans
Un tanque tiene\(f(t)\) litros de agua en el tiempo\(t\) medido en minutos, donde\(f(t) = -2.2t^3 +27t^2- 120t + 500\) (este modelo es válido\(t = 0\) para\(t = 9\)).
1. Esbozar las gráficas de\(f'(t)\) y\(f''(t)\).
2. ¿Qué es\(f'(t)\) la medición? ¿Cuál es el significado de\(f''(t)\)? Dar las unidades correctas.
  Imagina que el agua se escapa de un agujero. \(f'(t)\)es medir indirectamente el tamaño de ese agujero, ya que está midiendo la rapidez con la que se pierde agua en litros por minuto. \(f''(t)\)se relacionaría con la rapidez con la que se está abriendo o cerrando el agujero, midiendo así qué tan rápido está cambiando la tasa en litros por minuto por minuto.
  ans