5.1: Relaciones de recurrencia
- Page ID
- 116833
Como veremos en la siguiente sección, una ecuación diferencial se ve así:\(\frac{dP}{dt} = 0.03 \cdot P\). Sin embargo, de lo que quiero hablar primero son las relaciones de recurrencia. Permítanme presentarles estos con un truco de magia.
Escoge un número entre 1 y 100, y voy a adivinarlo. Pero no antes de mezclarlo un poco.
- Tome su número y divídalo por cinco, y redondee al número entero más cercano.
- Después agregue\(36\) al resultado.
- Repita los pasos (1) y (2) dos veces más, para un total de tres iteraciones.
¿Hecho? Apuesto a que terminaste con el número 45. ¿Estás asombrado?
Este truco se basa en la relación de recurrencia\(f_{t+1} = \frac{1}{5} f_t + 36\). Piense en\(f_t\) como el valor anterior, y\(f_{t+1}\) como el nuevo valor. ¿Cómo se llega de uno a otro? Bueno, ignorando el redondeo, divides\(5\) y agregas\(36\), y eso es exactamente lo que te\(f_{t+1} = \frac{1}{5} f_t + 36\) está diciendo que hagas. Para poder utilizar tal ecuación, necesitamos un valor inicial o\(f_0\). En el truco, este era el número original que escogiste. Vamos a crear una gráfica con el valor inicial\(f_0 = 100\):
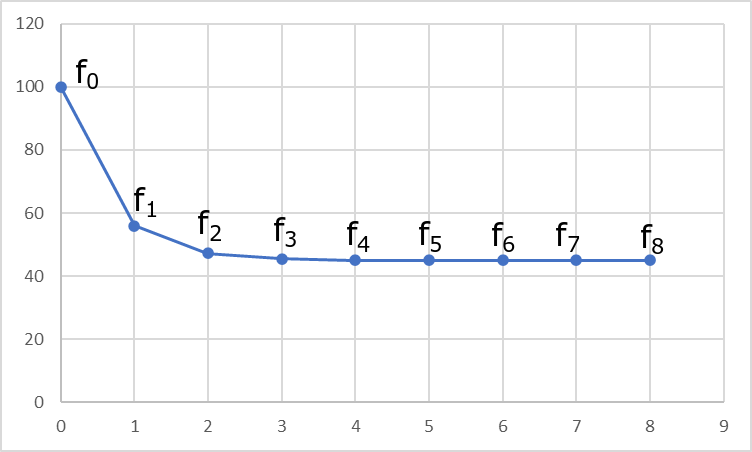
Como puede ver, esta relación de recurrencia converge rápidamente a\(f_t = 45\) por el momento\(t = 3\). ¡Por eso funciona el truco! Si empezamos en otro lugar, la gráfica se ve muy parecida y de todas formas converge a 45.
Sin embargo, las relaciones de recurrencia son útiles para algo más que trucos de magia.
Bueno, ya que esta es una relación de recurrencia, queremos relacionar la cantidad en consideración,\(h_t\) con su valor al año siguiente, que es\(h_{t+1}\). Entonces se verá algo así como
\(h_{t+1} = 1.5 h_t + 16\)
pero esos no son los valores correctos todavía — solo quiero tener una idea de hacia dónde va esto.
Lo primero que necesitamos codificar es la expansión por\(1\%\). Podemos tomar\(1\%\), o\(0.01\) y multiplicar por\(h_t\) así:\(0.01 h_t\). Pero el viejo bosque sigue ahí (a excepción de la tala, que nos preocuparemos en un segundo), así que\(h_t\) agreguemos también:\(0.01 h_t + h_t\). Si tenemos en cuenta\(h_t\), obtenemos
\[\begin{align*} 0.01 h_t + h_t & = h_t(0.01 + 1) \\ & = h_t(1.01) \\ & = 1.01 h_t \end{align*}\]
Este es el crecimiento por\(1\%\). ¿Qué pasa con esa tala? Bueno, eso no es un cambio porcentual, así que simplemente restaremos el\(2000\) para representar la pérdida de biomasa. Entonces nuestra relación de recurrencia final es—>
\(h_{t+1} = 1.01 h_t - 2000\)
Bueno, juguemos un poco con él y veamos qué pasa. Pero antes de que podamos hacer eso, necesitamos un valor inicial\(h_0\). Vamos a adivinar algo. Como estamos perdiendo\(2000\) un año, vamos a necesitar un número mucho mayor que\(2000\). Solo adivinemos que\(h_0\) son toneladas\(50,\!000\) métricas.
Ahora podemos calcular varios\(h_t\) valores:
\[\begin{align*} h_0 & = 50000 \\ h_1 & = 1.01(50000)-2000 = 48500 \\ h_2 & = 1.01(48500) - 2000 = 46985 \\ h_3 & = 1.01(46985) - 2000 \approx 45500 \\ \end{align*}\]
Podemos ver que la biomasa está bajando —no es una buena señal para el bosque. Podemos acelerar bastante estos cálculos en excel. Si haces eso, puedes ver que el bosque se habrá ido totalmente\(h_{29}\), en menos de treinta años. Sin embargo, esa no es una respuesta completa, ya que puede depender de la cantidad de biomasa con la que comencemos. Supongamos que es un bosque más grande con\(h_0 = 300,\!000\). Entonces vemos
\[\begin{align*} h_0 & = 300000 \\ h_1 & = 1.01(300000)-2000 = 301000 \\ h_2 & = 1.01(301000) - 2000 = 302010 \\ h_3 & = 1.01(302010) - 2000 \approx 303000 \\ \end{align*}\]
Y el bosque apenas crece a partir de ahí.
Veamos un ejemplo aún más complicado.
\[\begin{align*} f^0_{t+1} & = 5.23 f^3_t + 18.0 f^4_t + 24.55 f^{5+}_t \\ f^1_{t+1} & = 0.277 f^0_t \\ f^2_{t+1} & = 0.3405 f^1_t \\ f^3_{t+1} & = 0.4675 f^2_t \\ f^4_{t+1} & = 0.4675 f^3_t \\ f^{5+}_{t+1} & = 0.4675 f^4_t + 0.4675 f^{5+}_t \\ \end{align*}\]
Explique qué significa cada número en estas relaciones de recurrencia.
Dios mío, eso es un complicado lío de símbolos. Pero con un poco de paciencia, podemos resolverlo, creo.
Empecemos con la línea\(f^1_{t+1} = 0.277 f^0_t\). Sabemos por la declaración del problema que\(f^0_t\) son las truchas de 0 años de edad al año\(t\). La cantidad\(f^1_{t+1}\) es la cantidad de trucha de un año al año\(t+1\). Esta ecuación está relacionando el número de niños de un\(0\) año con el número de\(1\) años un año después. Lo que está diciendo es\(0.277\) veces el número de niños de cero años te da el número de niños de un año al año después. En otras palabras, esta ecuación está dando una tasa de\(27.7\%\) supervivencia desde la edad cero hasta la edad de uno.
A partir de aquí, ahora podemos decodificar fácilmente varias otras ecuaciones. \(f^2_{t+1} = 0.3405 f^1_t\)da una tasa de\(34.05\%\) supervivencia de uno a dos años. Lo similar encontramos tasa de\(46.75\%\) supervivencia de dos a tres años, y la misma tasa de tres a cuatro años. La ecuación\(f^{5+}_{t+1} = 0.4675 f^4_t + 0.4675 f^{5+}_t\) es un poco más complicada, ya que las truchas de 5 años provienen de las truchas de 4 años, pero también las de 5 años se mantienen dentro de esa categoría, por lo que hay dos formas de llegar allí. Ambos implican una tasa de\(46.75\%\) supervivencia.
Observe que estas tasas de supervivencia son bastante bajas para los estándares humanos. Sin embargo, hay algunas buenas noticias para la especie: mira la primera ecuación\(f^0_{t+1} = 5.23 f^3_t + 18.0 f^4_t + 24.55 f^{5+}_t\). ¿Qué opinas de esto? Así es — ¡estas son las nuevas truchas bebé! Como puede ver, hay muchos bebés nuevos que ayudan a equilibrar las bajas tasas de supervivencia que notamos antes. En particular, cada tres años produce aproximadamente 5 nuevas crías, cada cuatro años produce en promedio 18 nuevas crías, y un promedio de 5+ años produce casi 25 crías.
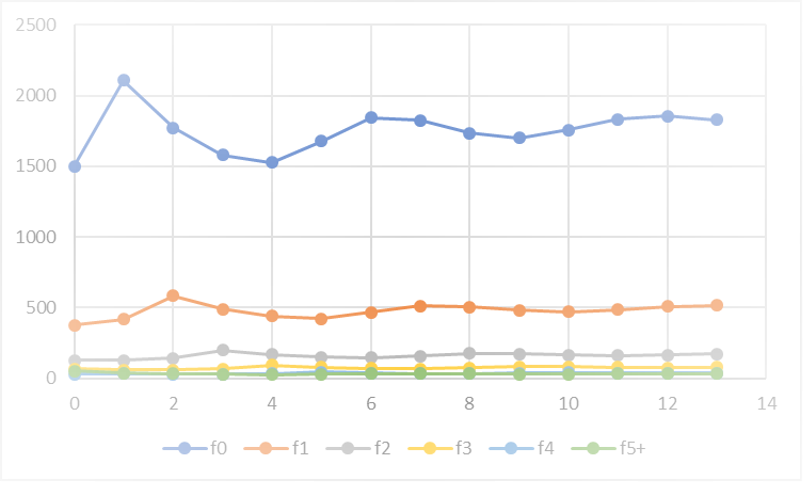
Creé esta gráfica en Excel (ver el archivo “cutthroat-life-cycle.xlsx” para las fórmulas y datos):
Y aquí están solo las últimas cuatro etapas para tener una mejor mirada a estas:
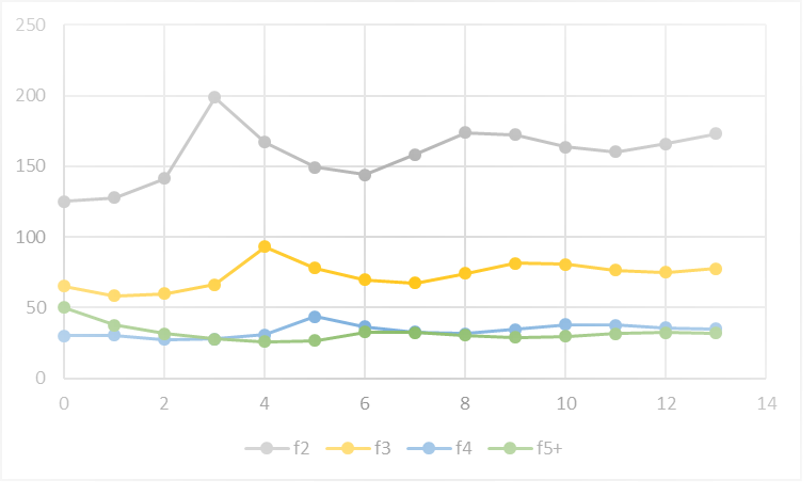
Como podemos ver, la población parece ser bastante estable. Una cosa que me destaca es cuántos peces de edad cero y edad uno hay en comparación con otros grupos.


