6.3: Tarea- Técnicas de Integración Numérica

1. Dada la imagen de\(f(x)\), encuentra las siguientes integrales definitivas.

   

   1. \(\int_{-2}^2 f(x)dx\).
      \(2\)

      ans
   2. \(\int_{2}^7 f(x)dx\).
      \(8\)

      ans
   3. \(\int_0^6 f(x)dx\).
      \(8\)

      ans
   4. \(\int_4^7 f(x)dx\).
      \(0\)

      ans
   5. \(\int_{-2}^7 f(x)dx\).
      \(10\)

      ans
   6. \(\int_{3}^3 f(x)dx\)(¿Qué crees que significa esto?)
      \(0\)— Se puede pensar en esto como un rectángulo infinitamente delgado.

      ans
   7. \(\int_{-1}^{0} f(x)dx\).
      \(1\)

      ans
   8. \(\int_{0}^{1.5} f(x)dx\).
      

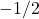      ans
   9. \(\int_{-1.5}^{4.5} f(x)dx\)
      \(10.5\)

      ans
2. ¿Recuerdas esos problemas de la tarea 1 donde empezamos con un gráfico de velocidad y luego dibujamos el gráfico de posición? Vamos a intentarlo de nuevo.

   

   1. Dibuja la gráfica de posición correspondiente a esta gráfica de velocidad junto a la gráfica anterior.
      

      ans
   2. Encuentra las siguientes tres integrales basadas en la gráfica original\(v(t)\):

      \(\int_0^3 v(t)dt, \quad \int_0^6 v(t)dt, \quad \int_0^9 v(t)dt.\)

      \(60\),\(30\),\(30\)

      ans
   3. Tus respuestas para las partes (a) y (b) deben tener el mismo aspecto de alguna manera. ¿Cómo se ven iguales y por qué funcionó de esta manera?
      Las respuestas son los\(y\) valores clave de la gráfica en la parte (a). Esto es lo mismo, ya que en ambos casos estás haciendo lo mismo: tomar\(\Delta x \cdot y\) (o\(\Delta t \cdot \text{velocity}\) y sumarlo a medida que avanzas.

      ans
3. Usando\(6\) rectángulos y usando la regla del rectángulo izquierdo, estime el área bajo la curva de las siguientes funciones de\(x = 0\) a\(x = 3\).
   1. \(e(x) = 2 - x\).
      \(\approx 2.25\)

      ans
   2. \(f(x) = -\frac{1}{9} x^2 + 1\)
      \(\approx 2.24\)

      ans
   3. \(g(x) = e^x\)
      \(\approx 14.71\)

      ans
4. Porque\(e(x)\) en el problema 3, encuentra el área exacta usando la fórmula para el área de un triángulo.
   \(1.5\)

   ans
5. Para\(f(x)\) en el problema 3:
   1. Si aún no lo has hecho, dibuja una imagen de la gráfica así como los rectángulos que usaste para aproximar el área.
   2. ¿Su aproximación del problema 3 es una sobreestimación o una subestimación? ¿Cómo lo sabes?
      Sobreestimar, ya que parece que los rectángulos cubren demasiada área.

      ans
6. Vea el video de Khan Academy sobre el método Trapezoidal para encontrar el área bajo la curva.
7. Usando\(6\) trapecios que coincidan con la altura de la gráfica, estime el área bajo la curva de las siguientes funciones de\(x = 0\) a\(x = 3\).
   1. \(e(x) = 2 - x\).
      \(1.5\)

      ans
   2. \(f(x) = -\frac{1}{9} x^2 + 1\)
      \(1.99\)

      ans
   3. \(g(x) = e^x\)
      \(19.48\)

      ans
8. Mira este video similar a Khan Academy sobre la fórmula del punto medio: haz clic aquí
9. Usando\(6\) rectángulos, use la regla de punto medio para aproximar el área bajo la curva de\(x = 0\) a\(x = 3\).
   1. \(e(x) = 2 - x\).
      \(1.5\)

      ans
   2. \(f(x) = -\frac{1}{9} x^2 + 1\)
      \(2.03\)

      ans
   3. \(g(x) = e^x\)
      \(18.31\)

      ans
10. No pude encontrar una explicación de Khan Academy sobre la regla de Simpson, así que aquí hay otro video de Patrick en Just Math Tutoring.
11. Usa la regla de Simpson para aproximar el área bajo la curva. Use\(6\) intervalos de\(x = 0\) a\(x = 3\).
    1. \(e(x) = 2 - x\).
       \(1.5\)

       ans
    2. \(f(x) = -\frac{1}{9} x^2 + 1\)
       \(2\)

       ans
    3. \(g(x) = e^x\)
       \(\approx 19.09\)

       ans
12. Tenga en cuenta que las respuestas reales para el área bajo la curva de\(x = 0\) a\(x = 3\) son
    1. \(1.5\)para\(e(x) = 2-x\).
    2. \(2\)para\(f(x) = -\frac{1}{9} x^2 + 1\)
    3. \(19.086\)para\(g(x) = e^x\).

    Dadas estas respuestas, califique las siguientes reglas de más precisas a menos precisas en función de las respuestas de esta tarea: regla del rectángulo izquierdo, regla trapezoidal, regla del punto medio, regla de Simpson.