2: Estructura Especial y Soluciones de ODEs
- Page ID
- 113662
Un tema consistente en todas las ODE es que la “estructura especial” de las ecuaciones puede revelar información sobre la naturaleza de las soluciones. Aquí nos fijamos en una propiedad muy básica e importante de las ecuaciones autónomas:
“Los cambios de tiempo de las soluciones de las ODEs autónomas también son soluciones de la ODE (pero con una condición inicial diferente)”.
Ahora vamos a mostrar cómo ver esto.
A lo largo de este curso asumiremos que la existencia y singularidad de las soluciones se mantiene en un dominio e intervalo de tiempo suficiente para nuestros argumentos y cálculos.
Comenzamos por establecer el escenario. Consideramos un campo vectorial autónomo definido en\(\mathbb{R}^n\):
\[\dot{x} = f(x) \quad x(0) = x_{0}, \quad x \in \mathbb{R}^n, \label{2.1}\]
con solución denotada por:
\[x(t, 0, x_{0}), \,x(0, 0, x_{0}) = x_{0}.\]
Aquí nos estamos tomando el tiempo inicial para estar\(t_{0} = 0\). Veremos, en breve, que para las ecuaciones autónomas esto se puede hacer sin pérdida de generalidad. Ahora elegimos\(s \in \mathbb{R}\) (\(s \ne 0\), que debe considerarse como una constante fija). Debemos mostrar lo siguiente:
\[\dot{x}(t+s) = f(x(t+s))\label{2.2}\]
Esto es lo que queremos decir con la frase los cambios de tiempo de las soluciones son soluciones. Esta relación se desprende inmediatamente del cálculo de la regla de la cadena:
\[\frac{d}{dt} = \frac{d}{d(t+s)} \frac{d(t+s)}{dt} = \frac{d}{d(t+s)}. \label{2.3}\]
Finalmente, necesitamos determinar la condición inicial para la solución desplazada en el tiempo. Para la solución original tenemos:
\[x(t, 0, x_{0}), x(0, 0, x_{0}) = x_{0}, \label{2.4}\]
y para la solución de cambio de tiempo tenemos:
\[x(t + s, 0, x_{0}), x(s, 0, x_{0}). \label{2.5}\]
Es por ello que, sin pérdida de generalidad, para los campos vectoriales autónomos podemos tomar el tiempo inicial para ser\(t_{0} = 0\). Esto nos permite simplificar los argumentos en la notación para soluciones de campos vectoriales autónomos, es decir,\(x(t, 0, x_{0}) \equiv x(t, x_{0})\) con\(x(0, 0, x_{0}) = x(0, x_{0}) = x_{0}\).
Ejemplo\(\PageIndex{5}\): The time-shift property of autonomous vector fields
Considere el siguiente campo vectorial autónomo unidimensional:
\[\dot{x} = \lambda x, x(0) = x_{0}, x \in \mathbb{R}, \lambda \in \mathbb{R}. \nonumber\]
La solución viene dada por:
\[x(t, 0, x_{0}) = x(t, x_{0}) = e^{\lambda t}x_{0}. \nonumber\]
La solución desplazada en el tiempo viene dada por:
\[x(t+s, x_{0}) = e^{\lambda (t+s)}x_{0}. \nonumber\]
Vemos que es una solución de la ODE con los siguientes cálculos:
\[\frac{d}{dt}x(t+s, x_{0}) = \lambda e^{\lambda (t+s)}x_{0} = \lambda x(t+s, x_{0}), \nonumber\]
con condición inicial:
\[x(s, x_{0}) = e^{\lambda s}x_{0}. \nonumber\]
En resumen, vemos que las soluciones de los campos vectoriales autónomos satisfacen las siguientes tres propiedades:
- \(x(0, x_{0}) = x_{0}\)
- \(x(t, x_{0})\)está\(C^{r}\) en\(x_{0}\)
- \(x(t+s, x_{0}) = x(t, x(s, x_{0}))\)
La propiedad uno solo refleja la notación que hemos adoptado. La propiedad 2 es una declaración de las propiedades que surgen de la existencia y singularidad de las soluciones. La propiedad 3 utiliza dos características de soluciones. Una es la propiedad de “cambio de tiempo” para campos vectoriales autónomos que hemos probado. El otro es “singularidad de soluciones” ya que el lado izquierdo y el lado derecho del Inmueble 3 satisfacen la misma condición inicial en t = 0.
Estas tres propiedades son las propiedades definitorias de un flujo, es decir, a. En otras palabras, vemos las soluciones como definiendo un mapa de puntos en el espacio de fases. La propiedad del grupo surge de la propiedad 3, es decir, la propiedad de cambio de tiempo. Para enfatizar esta propiedad de “mapa de espacio de fase” introducimos una notación general para el flujo de la siguiente manera
\[x(t, x_{0}) \equiv \phi_{t}(\cdot) \nonumber\]
donde el “·” en el argumento de\(\phi_{t}(\cdot)\) refleja el hecho de que el flujo es una función sobre el espacio de fase. Con esta notación las tres propiedades de un flujo se escriben de la siguiente manera:
- \(\phi_{0}(\cdot)\)es el mapa de identidad.
- \(\phi_{t}(\cdot)\)es\(C^r\) por cada t.
- \(\phi_{t+s}(\cdot) = \phi_{t} \circ \phi_{s}(\cdot)\)
A menudo usamos la frase “el flujo generado por el campo vectorial (autónomo)”. Autónomo está entre paréntesis ya que se entiende que cuando estamos considerando flujos entonces estamos considerando las soluciones de campos vectoriales autónomos. Esto se debe a que los campos vectoriales no autónomos no necesariamente satisfacen la propiedad time-shift, como ahora mostramos con un ejemplo.
Ejemplo\(\PageIndex{6}\): An example of a nonautonomous vector field not having the time-shift property
Considere el siguiente campo vectorial unidimensional en\(\mathbb{R}\):
\[\dot{x} = \lambda tx\), \)x(0) = x_{0}, x \in \mathbb{R}\), \(\lambda \in \mathbb{R}. \nonumber\]
Este campo vectorial es separable y la solución se encuentra fácilmente para ser:
\[x(t, 0, x_{0}) = x_{0}e^{\frac{\lambda}{2}t^2}. \nonumber\]
La ''solución” desplazada en el tiempo viene dada por:
\[x(t+s, 0, x_{0}) = x_{0}e^{\frac{\lambda}{2}(t+s)^2}. \nonumber \]
Mostramos que esto no satisface el campo vectorial con el siguiente cálculo:
\(\frac{d}{dt}x(t+s, 0, x_{0}) = x_{0}e^{\frac{\lambda}{2}(t+s)^2}\lambda (t+s)\).
\(\ne \lambda tx(t+s, 0, x_{0})\).
Quizás un ejemplo más simple que ilustra que los campos vectoriales no autónomos no satisfacen la propiedad de desplazamiento de tiempo es el siguiente.
Ejemplo\(\PageIndex{7}\)
Considere el siguiente campo vectorial unidimensional no autónomo:
\(\dot{x} = e^{t}\),\(x \in \mathbb{R}\).
La solución viene dada por:
\(x(t) = e^t\).
Es fácil verificar que la función de desplazamiento de tiempo:
\(x(t+s) = e^{t+s}\),
no satisface la ecuación.
En el estudio de las ODE ciertos tipos de soluciones han alcanzado un nivel de prominencia basado en gran parte en su significación en las aplicaciones. Ellos son
- soluciones de equilibrio,
- soluciones periódicas,
- soluciones heteroclínicas,
- soluciones homoclínicas.
Definimos cada uno de estos.
DEFINICIÓN 8: EL
Un punto en el espacio de fase\(x = \bar{x} = \mathbb{R}^n\) que es una solución de la ODE, i.e.
\(f(\bar{x}) = 0, f(\bar{x}, t) = 0\),
se llama punto de equilibrio.
Por ejemplo, x = 0 es un punto de equilibrio para los siguientes campos vectoriales unidimensionales autónomos y no autónomos, respectivamente,
- \(\dot{x} = x\),\(x \in \mathbb{R}\),
- \(\dot{x} = tx\),\(x \in \mathbb{R}\).
Una solución periódica es simplemente una solución que es periódica en el tiempo. Su definición es la misma para los campos vectoriales tanto autónomos como no autónomos.
DEFINICIÓN 9: Soluciones periódicas
Una solución\(x(t, t_{0}, x_{0})\) es periódica si existe una T > 0 tal que
\(x(t, t_{0}, x_{0}) = x(t+T, t_{0}, x_{0})\)
Las soluciones homoclínicas y heteroclínicas son importantes en una variedad de aplicaciones. Su definición no es tan simple como las definiciones de equilibrio y soluciones periódicas ya que pueden definirse y generalizarse a muchos escenarios diferentes. Solo consideraremos estas soluciones especiales para campos vectoriales autónomos, y soluciones homoclínicas o heteroclínicas a soluciones de equilibrio.
DEFINICIÓN 10 (SOLUCIONES HOMOCLÍNICAS Y
Supongamos\(\bar{x}_{1}\) y\(\bar{x}_{2}\) son puntos de equilibrio de un campo vectorial autónomo, i.e.
\(f(\bar{x}_{1}) = 0\),\(f(\bar{x}_{2}) = 0\).
Se dice que una trayectoria\(x(t, t_{0}, x_{0})\) es heteroclínica a\(\bar{x}_{1}\) y\(\bar{x}_{2}\) si
\(lim_{t \rightarrow \infty} x(t, t_{0}, x_{0}) = \bar{x}_{2}\),
\[lim_{t \rightarrow -\infty} x(t, t_{0}, x_{0}) = \bar{x}_{1}, \label{2.11}\]
Si\(\bar{x}_{1} = \bar{x}_{2}\) se dice que la trayectoria es homoclínica a\(\bar{x}_{1} = \bar{x}_{2}\).
Ejemplo\(\PageIndex{8}\): equilibrium points and heteroclinic orbits
Considere el siguiente campo vectorial autónomo unidimensional en\(\mathbb{R}\):
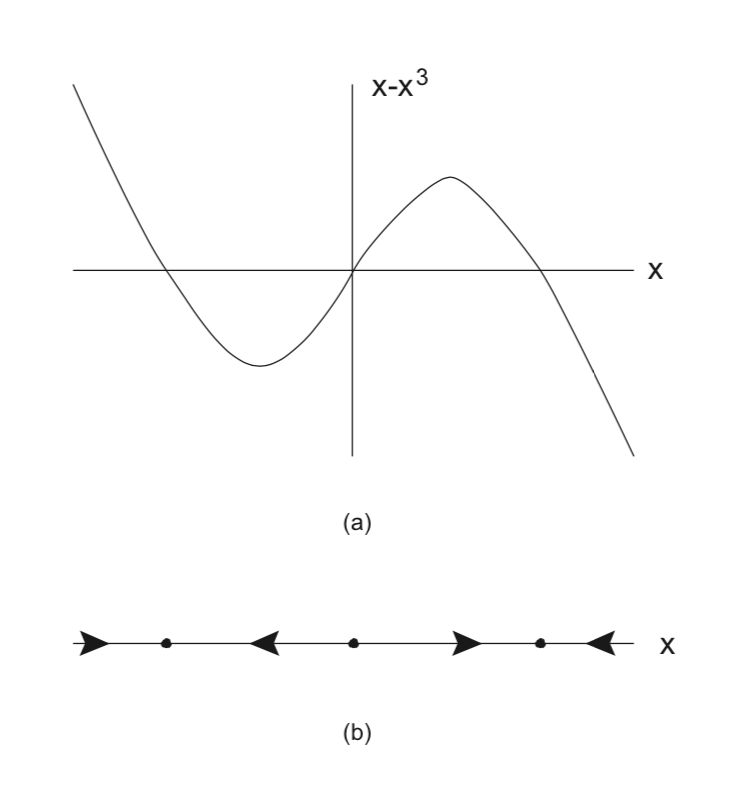
\[\dot{x} = x-x^3 = x(1-x^2), x \in \mathbb{R}. \label{2.12}\]
Este campo vectorial tiene tres puntos de equilibrio en\(x = 0, \pm 1\).
En la Fig. 2.1 mostramos la gráfica del campo vectorial (2.12) en el panel a) y la dinámica de la línea de fase en el panel b).
Los puntos negros sólidos en el panel b) corresponden a los puntos de equilibrio y estos, a su vez, corresponden a los ceros del campo vectorial mostrado en el panel a). Entre sus ceros, el campo vectorial tiene un signo fijo (es decir, positivo o negativo), correspondiente a que sea creciente o decreciente. Esto se indica por la dirección de las flechas en el panel b).
Nuestra discusión sobre trayectorias, así como este ejemplo, nos lleva a un punto en el que es natural introducir la importante noción de un conjunto invariante. Si bien esta es una idea general que aplica tanto a los sistemas autónomos como a los no autónomos, en este curso solo discutiremos esta noción en el contexto de los sistemas autónomos. En consecuencia, vamos a\(\phi_{t}(\cdot)\) denotar el flujo generado por un campo vectorial autónomo.
DEFINICIÓN 11: INVARIANTE
Se dice que un conjunto\(M \subset \mathbb{R}^n\) es invariante si
\[x \in M \Rightarrow \phi_{t}(x) \in M\]
\(\forall t\).
En otras palabras, un conjunto es invariante (con respecto a un flujo) si se inicia en el conjunto, y permanece en el conjunto, para siempre.
Si lo piensas, debería quedar claro que los conjuntos invariantes son conjuntos de trayectorias. Cualquier trayectoria única es un conjunto invariante. Todo el espacio de fase es un conjunto invariante. Los casos más interesantes son los “intermedios”. Además, debe quedar claro que la unión de dos conjuntos invariantes cualesquiera es también un conjunto invariante (solo aplique la definición de conjunto invariante a la unión de dos, o más, conjuntos invariantes).
Hay ciertas situaciones en las que nos interesarán conjuntos que son invariantes solo por tiempo positivo, conjuntos invariantes positivos.
DEFINICIÓN 12: SET INVARIANTE
Se dice que un conjunto\(M \subset \mathbb{R}^n\) es invariante positivo si
\(x \in M \Rightarrow \phi_{t}(x) \in M\)\(\forall t>0\).
Existe una noción similar de conjuntos invariantes negativos, pero la generalización de esto a partir de la definición de conjuntos invariantes positivos debería ser obvia, por lo que no vamos a escribir los detalles.
En cuanto al ejemplo 8, los tres puntos de equilibrio son conjuntos invariantes, así como los intervalos cerrados\([-1, 0]\) y [0, 1]. ¿Hay otros conjuntos invariantes?


