4: Comportamiento cerca de trayectorias - Linealización

Ahora vamos a discutir un método para analizar la estabilidad que utiliza linealización sobre el objeto cuya estabilidad es de interés. Por ahora, los “objetos de interés” son soluciones específicas de un campo vectorial.La estructura de las soluciones de los sistemas lineales de coeficientes constantes está cubierta en muchos libros de texto de ODE. Mi favorito es el libro de Hirsch et al.1. Cubre todo el álgebra lineal necesaria para analizar ODEs lineales que probablemente no cubriste en tu curso de álgebra lineal. El libro de Arnold también es muy bueno, pero la presentación es más compacta, con menos ejemplos.

Comenzamos considerando un campo vectorial general no autónomo:

\[\dot{x} = f(x, t), x \in \mathbb{R}^n, \label{4.1}\]

y suponemos que

\[\bar{x}(t, t_{0}, x_{0}), \label{4.2}\]

es la solución de la Ecuación\ ref {4.1} para la cual deseamos determinar sus propiedades de estabilidad. Al igual que cuando introdujimos las definiciones de estabilidad, procedemos localizando el campo vectorial sobre la solución de interés. Esto lo hacemos introduciendo el cambio de coordenadas

\(x = y+\bar{x}\)

para la Ecuación\ ref {4.1} como sigue:

\(\dot{x} = \dot{y}+\dot{\bar{x}} = f(y+\bar{x}, t)\),

o

\(\dot{y} = f(y+\bar{x}, t)\dot{\bar{x}}\),

\[= f(y+\bar{x}, t)f(\bar{x}, t), \label{4.3}\]

donde omitimos los argumentos de en\(\bar{x}(t, t_{0}, x_{0})\) aras de una notación menos engorrosa. A continuación, Taylor nos\(f(y+\bar{x}, t)\) expandimos\(y\) sobre la solución\(\bar{x}\), pero solo requeriremos los términos de orden líder explícitamente

\[f(y+\bar{x}, t) = f(\bar{x}, t)+Df(\bar{x},t)y+\mathbb{O}(|y|^2), \label{4.4}\]

donde\(Df\) denota la derivada (es decir, matriz jacobiana) de la función valorada por vector f y\(\mathbb{O}(|y|^2)\) denota términos de orden superior en la expansión de Taylor que no necesitaremos en forma explícita. Sustituyendo esto en la Ecuación\ ref {4.4} da:

\(\dot{y} = f(y+\bar{x}, t) - f(\bar{x}, t)\),

\(= f(\bar{x}, t)+Df(\bar{x}, t)y+\mathbb{O}(|y|^2)f(\bar{x}, t)\),

\[= Df(\bar{x}, t)y+\mathbb{O}(|y|^2). \label{4.5}\]

Tenga en cuenta que nos interesa el comportamiento de las soluciones cercanas\(\bar{x}(t, t_{0}, x_{0})\), es decir, para\(y\) pequeños. Por lo tanto, en esa situación parece razonable que descuidar la\(\mathbb{O}(|y|^2)\) en la Ecuación\ ref {4.5} sería una aproximación que nos proporcionaría la información particular que buscamos. Por ejemplo, ¿nos proporcionaría información suficiente para disuadir la estabilidad de las minas? En particular,

\[\dot{y} = Df(\bar{x}, t)y, \label{4.6}\]

se conoce como la linealización del campo vectorial\(\dot{x} = f (x, t)\) sobre la solución\(\bar{x}(t, t_{0}, x_{0})\).

Antes de responder a la pregunta de si la Ecuación\ ref {4.1} proporciona o no una aproximación adecuada a las soluciones de la Ecuación\ ref {4.5} para y “small”, primero estudiaremos los campos vectoriales lineales por su cuenta.

Los campos vectoriales lineales también se pueden clasificar como no autónomos o autónomos. Los campos vectoriales lineales no autónomos se obtienen linealizando un campo vectorial no autónomo alrededor de una solución (y conservando solo los términos lineales). Tienen la forma general:

\[\dot{y} = A(t)y, y(0) = y_{0}, \label{4.7}\]

donde

\[A(t) \equiv Df(\bar{x}(t, t_{0}, x_{0}), t) \label{4.8}\]

es una\(n \times n\) matriz. También se pueden obtener linealizando un campo vectorial autónomo sobre una solución dependiente del tiempo.

Se obtiene un campo vectorial lineal autónomo linealizando un campo vectorial autónomo alrededor de un punto de equilibrio. Más precisamente, vamos a\(\dot{x} = f(x)\) denotar un campo vectorial autónomo y dejar\(x = x_{0}\) denotar un punto de equilibrio, i.e\(f(x_{0}) = 0\). El campo vectorial autónomo linealizado sobre este punto de equilibrio tiene la forma:

\[\dot{y} = Df(x_{0})y, y(0) = y_{0}, \label{4.9}\]

o

\[\dot{y} = Ay, y(0) = y_{0}, \label{4.10}\]

donde\(A \equiv Df(x_{0})\) es una\(n \times n\) matriz de números reales. Esto es significativo porque (4.10) se puede resolver utilizando técnicas de álgebra lineal, pero la Ecuación\ ref {4.7}, en general, no se puede resolver de esta manera. De ahí que ahora describiremos la solución general de (4.10).

La solución general de la Ecuación\ ref {4.10} viene dada por:

\[y(t) = e^{At}y_{0}. \label{4.11}\]

Para verificar que esta es la solución, simplemente necesitamos sustituir por el lado derecho y el lado izquierdo de (4.10) y demostrar que la igualdad se mantiene. Sin embargo, primero necesitamos explicar qué\(e^{At}\) es, es decir, el exponencial de la\(n \times n\) matriz A (examinando la Ecuación\ ref {4.11} debe quedar claro que si la Ecuación\ ref {4.11} va a tener sentido matemáticamente, entonces\(e^{At}\) debe ser una\(n times n\) matriz).

Al igual que el exponencial de un escalar, el exponencial de una matriz se define a través de la serie exponencial de la siguiente manera:

\(e^{At} \equiv \mathbb{I}+At+\frac{1}{2!}A^{2}t^{2}+···+\frac{1}{n!}A^{n}t^{n}+\cdots\),

\[= \sum_{i=0}^{n}\frac{1}{i!}A^{i}t^{i}, \label{4.12}\]

donde\(\mathbb{I}\) denota la matriz de\(n \times n\) identidad. Pero aún debemos responder a la pregunta, “¿tiene sentido matemático esta serie exponencial que involucra productos de matrices”? Ciertamente podemos computar productos de matrices y multiplicarlos por escalares. Pero tenemos que darle sentido a una suma infinita de tales objetos matemáticos. Esto lo hacemos definiendo la norma de una matriz y luego considerando la convergencia de la serie en norma. Cuando esto se hace el “problema de convergencia” es exactamente el mismo que el del exponencial de un escalar. Por lo tanto, la serie exponencial para una matriz converge absolutamente para todos t, y por lo tanto se puede diferenciar con respecto a t término por término, y la serie resultante de derivados también converge absolutamente.

A continuación tenemos que argumentar que la Ecuación\ ref {4.11} es una solución de la Ecuación\ ref {4.10}. Si diferenciamos la serie (4.12) término por término, obtenemos que:

\[\frac{d}{dt}e^{At} = Ae^{At} = e^{At}A, \label{4.13}\]

donde hemos utilizado el hecho de que las matrices A y\(e^{At}\) conmutan (esto es fácil de deducir del hecho de que A conmuta con cualquier potencia de A) Se deduce entonces de este cálculo que:

\[\dot{y} = \frac{d}{dt}e^{At}y_{0} = Ae^{At}y_{0} = Ay. \label{4.14}\]

Por lo tanto, el problema general de resolver (4.10) equivale a la computación\(e^{At}\), y ahora volvemos nuestra atención a esta tarea.

Primero, supongamos que\(A\) es una matriz diagonal, digamos

\[A = \begin{pmatrix} {\lambda_{1}}&{0}&{\cdots}&{0}\\ {0}&{\lambda_{2}}&{\cdots}&{0}\\ {0}&{0}&{\cdots}&{0}\\ {0}&{0}&{\cdots}&{\lambda_{n}} \end{pmatrix} \label{4.15}\]

Entonces es fácil ver sustituyendo A en la serie exponencial (4.12) que:

\[e^{At} = \begin{pmatrix} {e^{\lambda_{1}t}}&{0}&{\cdots}&{0}\\ {0}&{e^{\lambda_{2}t}}&{\cdots}&{0}\\ {0}&{0}&{\cdots}&{0}\\ {0}&{0}&{\cdots}&{e^{\lambda}t} \end{pmatrix} \label{4.16}\]

Por lo tanto nuestra estrategia será transformar coordenadas para que en las nuevas coordenadas A se convierta en diagonal (o lo más “cerca posible” de la diagonal, lo que explicaremos en breve). Entonces\(e^{At}\) será fácilmente computable en estas coordenadas. Una vez que eso se logra, entonces usamos la inversa de la transformación para transformar la solución de nuevo al sistema de coordenadas original.

Ahora hacemos estas ideas precisas. Dejamos

\[y = Tu, u \in \mathbb{R}^n, y \in \mathbb{R}^n, \label{4.17}\]

donde T es una\(n \times n\) matriz cuyas propiedades precisas se desarrollarán en lo siguiente.

Este es un enfoque típico en las ODE. Proponemos una transformación coordinada general de la ODE, y luego la construimos de una manera que da las propiedades de la ODE que deseamos. Sustituir (4.17) en (4.10) da:

\[\dot{y} = T\dot{u} = Ay = ATu, \label{4.18}\]

T se construirá de una manera que la haga invertible, de manera que tengamos:

\[\dot{u} = T^{-1}ATu, u(0) = T^{-1}y(0). \label{4.19}\]

Para simplificar la notación dejamos:

\[T = T^{-1}AT, \label{4.20}\]

o

\[A = T^{-1}\Lambda T. \label{4.21}\]

Sustituir (4.21) en la serie por la matriz exponencial (4.12) da:

\(e^{At} = e^{T\Lambda T^{-1}t}\),

\[= \mathbb{1}+ T\Lambda T^{-1}t+\frac{1}{2!}(T\Lambda T^{-1})^{2}t^2+\cdots+\frac{1}{n!}(T\Lambda T^{-1})^{n}t^n+\cdots \label{4.22}\]

Ahora tenga en cuenta que para cualquier entero positivo n tenemos:

\((T\Lambda T^{-1})^{n} = \underbrace{(T\Lambda T^{-1})(T\Lambda T^{-1})\cdots (T\Lambda T^{-1})(T\Lambda T^{-1})}_{n factors}\)

\[= T\Lambda^{n}T^{-1} \label{4.23}\]

Sustituir esto en (4.22) da:

\(e^{At} = \sum_{n=0}^{\infty} \frac{1}{n!}(T\Lambda T^{-1})^{n}t^n\),

\(= T(\sum_{n=0}^{\infty} \frac{1}{n!}\Lambda^{n}t^n)T^{-1}\),

\[= Te^{\Lambda t}T^{-1} \label{4.24}\]

o

\[e^{At} = Te^{\Lambda t}T^{-1} \label{4.25}\]

Ahora llegamos a nuestro principal resultado. Si T se construye de manera que

\[\Lambda = T^{-1}AT \label{4.26}\]

es diagonal, entonces se deduce de (4.16) y (4.25) que siempre se\(e^{At}\) puede computar. Entonces el problema de la ODE de resolver (4.10) se convierte en un problema en álgebra lineal. Pero, ¿se puede diagonalizar siempre una\(n \times n\) matriz general A? Si has tenido un curso de álgebra lineal, sabes que la respuesta a esta pregunta es “no”. Hay una teoría de lo (real) que se aplicará aquí. No obstante, eso nos llevaría a un desvío demasiado grande para este curso. En cambio, consideraremos los tres casos estándar para\(2 \times 2\) matrices. Eso bastará para introducir las ideas principales sin empantanarse en álgebra lineal. Sin embargo, no se puede evitar por completo. Tendrá que ser capaz de calcular los valores propios y los vectores propios de\(2 \times 2\) las matrices, y comprender su significado.

Los tres casos de\(2 \times 2\) matrices que consideraremos se caracterizan por sus valores propios:

• dos valores propios reales, diagonalizables A,
• dos valores propios idénticos, A no diagonalizable,
• un par conjugado complejo de valores propios.

En la siguiente tabla resumimos la forma en la que se pueden transformar estas matrices (referidas como la de A) y la exponencial resultante de esta forma canónica.

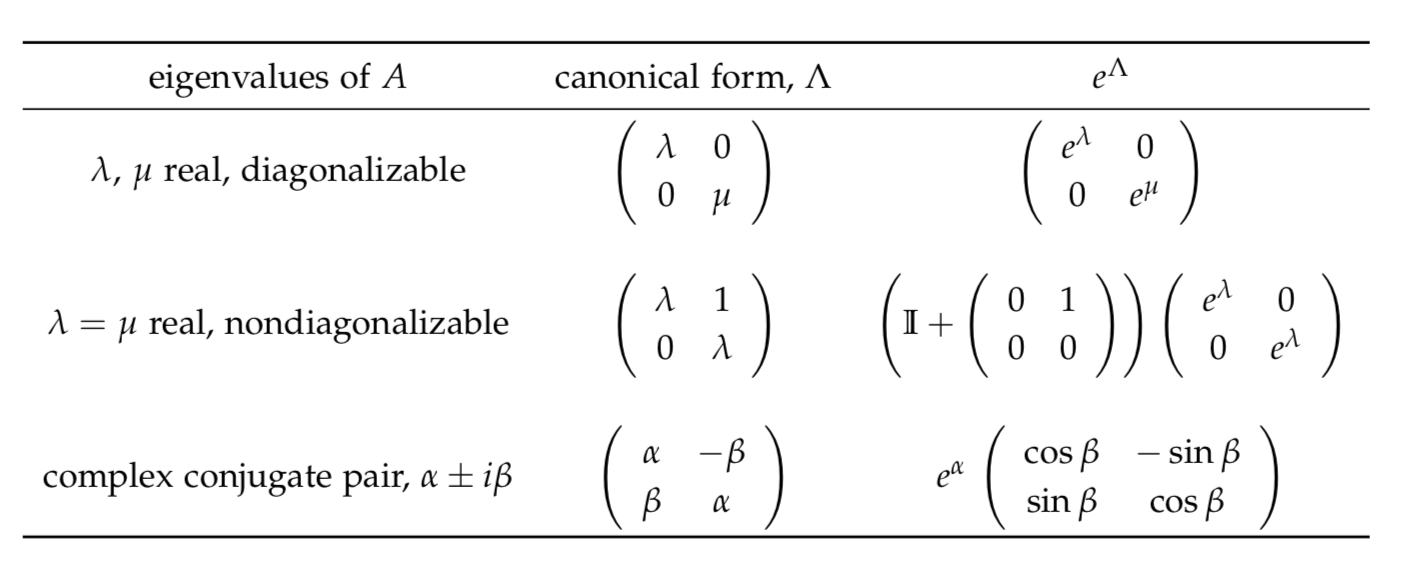
Una vez\(\Lambda\) realizada la transformación a, utilizaremos estos resultados para deducir\(e^{\Lambda}\).