5: Comportamiento cerca de Equilbria - Linealización
- Page ID
- 113586
Ahora consideraremos varios ejemplos para resolver, y comprender, la naturaleza de las soluciones, de
\[\dot{x} = Ax, x \in \mathbb{R}^2. \label{5.1}\]
Para todos los ejemplos, el método para resolver el sistema es el mismo.
Pasos para resolver
- Paso 1. Calcular los valores propios de\(A\).
- Paso 2. Calcular los vectores propios de\(A\).
- Paso 3. Utilice los vectores propios de\(A\) para formar la matriz de transformación\(T\).
- Paso 4. Computar\(\Lambda = T^{-1}AT\).
- Paso 5. Computar\(e^{At} = Te^{\lambda t}T^{-1}\).
Una vez que hemos calculado\(e^{At}\) tenemos la solución de la Ecuación\ ref {5.1} a través de cualquier condición inicial\(y_{0}\) ya que\(y(t)\)\(y(0) = y_{0}\),, viene dada por\(y(t) = e^{At}y_{0}\).
Ejemplo\(\PageIndex{10}\)
Consideramos la siguiente ODE lineal y autónoma:
\[\begin{pmatrix} {\dot{x_{1}}}\\ {\dot{x_{2}}} \end{pmatrix} = \begin{pmatrix} {2}&{1}\\ {1}&{2} \end{pmatrix} \begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix} \label{5.2}\]
donde
\[A = \begin{pmatrix} {2}&{1}\\ {1}&{2} \end{pmatrix}, \label{5.3}\]
Paso 1. Calcular los valores propios de A.
Los valores propios de A, denotan por\(\lambda\), están dados por las soluciones del polinomio característico:
\(det \begin{pmatrix} {2-\lambda}&{1}\\ {1}&{2-\lambda} \end{pmatrix} = (2-\lambda)^2-1 = 0\)
\[= \lambda^{2}-4\lambda+3 = 0, \label{5.4}\]
o
\(\lambda_{1,2} = 2 \pm \frac{1}{2}\sqrt{16-12} = 3, 1\)
Paso 2. Calcular los vectores propios de A.
Para cada valor propio, calculamos el vector propio correspondiente. El vector propio correspondiente al valor propio 3 se encuentra resolviendo:
\[\begin{pmatrix} {2}&{1}\\ {1}&{2} \end{pmatrix} \begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix} = 3\begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix}, \label{5.5}\]
o
\[2x_{1}+x_{2} = 3x_{1}, \label{5.6}\]
\[x_{1}+2x_{2} = 3x_{2}. \label{5.7}\]
Ambas ecuaciones dan la misma ecuación ya que las dos ecuaciones son dependientes:
\[x_{2} = x_{1} \label{5.8}\].
Por lo tanto tomamos como el autovector correspondiente al valor propio 3:
\[\begin{pmatrix} {1}\\ {1} \end{pmatrix} \label{5.9}\]
A continuación calculamos el vector propio correspondiente al valor propio 1. Esto viene dado por una solución a las siguientes ecuaciones:
\[\begin{pmatrix} {2}&{1}\\ {1}&{2} \end{pmatrix} \begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix} = \begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix}, \label{5.10}\]
o
\[2x_{1}+x_{2} = x_{1}, \label{5.11}\]
\[x_{1}+2x_{2} = x_{2}. \label{5.12}\]
Ambas ecuaciones dan la misma ecuación:
\[x_{2} = -x_{1}. \label{5.13}\]
Por lo tanto tomamos como el autovector correspondiente al valor propio:
\[\begin{pmatrix} {1}\\ {-1} \end{pmatrix} \label{5.14}\]
Paso 3. Utilice los vectores propios de A para formar la matriz de transformación T.
Para las columnas de\(T\) tomamos los vectores propios correspondientes a los autovalores 1 y 3:
\[T = \begin{pmatrix} {1}&{1}\\ {-1}&{1} \end{pmatrix} \label{5.15}\]
con la inversa dada por:
\[T^{-1} = \frac{1}{2}\begin{pmatrix} {1}&{-1}\\ {1}&{1} \end{pmatrix} \label{5.16}\]
Paso 4. Cómputos\(\Lambda = T^{-1}AT\).
Contamos con:
\(T^{-1}AT = \dfrac{1}{2}\begin{pmatrix} {1}&{-1}\\ {1}&{1} \end{pmatrix} \begin{pmatrix} {2}&{1}\\ {1}&{2} \end{pmatrix} \begin{pmatrix} {1}&{1}\\ {-1}&{1} \end{pmatrix}\)
\( = \frac{1}{2}\begin{pmatrix} {1}&{-1}\\ {1}&{1} \end{pmatrix} \begin{pmatrix} {1}&{3}\\ {-1}&{3} \end{pmatrix}\)
\[= \begin{pmatrix} {1}&{0}\\ {0}&{3} \end{pmatrix} \equiv \Lambda \label{5.17}\]
Por lo tanto, en las\(u_{1}-u_{2}\) coordenadas (5.2) se convierte en:
\[\begin{pmatrix} {\dot{u_{1}}}\\ {\dot{u_{2}}} \end{pmatrix} = \begin{pmatrix} {1}&{0}\\ {0}&{3} \end{pmatrix} \begin{pmatrix} {u_{1}}\\ {u_{2}} \end{pmatrix} \label{5.18}\]
En las\(u_{1}-u_{2}\) coordenadas es fácil ver que el origen es un punto de equilibrio inestable.
Paso 5. Cómputos\(e^{At} = Te^{\lambda t}T^{-1}\).
Contamos con:
\(e^{AT} = \frac{1}{2}\begin{pmatrix} {1}&{1}\\ {-1}&{1} \end{pmatrix} \begin{pmatrix} {e^{t}}&{0}\\ {0}&{e^{3t}} \end{pmatrix} \begin{pmatrix} {1}&{-1}\\ {1}&{1} \end{pmatrix}\)
\(= \frac{1}{2}\begin{pmatrix} {1}&{1}\\ {-1}&{1} \end{pmatrix} \begin{pmatrix} {e^{t}}&{-e^{t}}\\ {e^{3t}}&{e^{3t}} \end{pmatrix}\)
\[= \begin{pmatrix} \frac{1}{2}{e^{t}+e^{3t}}&{-e^{t}+e^{3t}}\\ {-e^{t}+e^{3t}}&{e^{t}+e^{3t}} \end{pmatrix} \label{5.19}\]
Vemos que el origen también es inestable en las\(x_{1}-x_{2}\) coordenadas originales. Se le conoce como fuente, y esto se caracteriza por el hecho de que todos los valores propios de A tienen parte real positiva. El retrato de fase se ilustra en la Fig. 5.1.
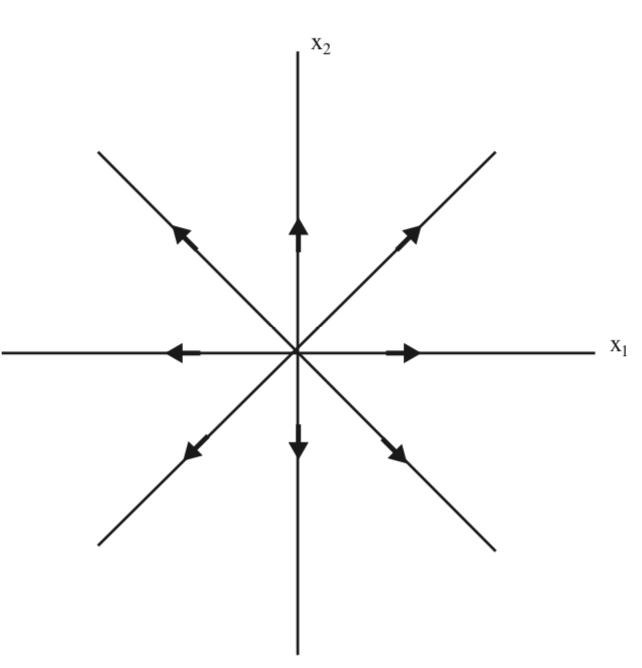
Comentamos esto es posible inferir el comportamiento de\(e^{At}\) como a\(t \rightarrow \infty\) partir del comportamiento de\(e^{\Lambda t}\) as\(t \rightarrow \infty\) ya que T no depende de t.
Ejemplo\(\PageIndex{11}\)
Consideramos la siguiente ODE lineal y autónoma:
\[\begin{pmatrix} {\dot{x_{1}}}\\ {\dot{x_{2}}} \end{pmatrix} = \begin{pmatrix} {-1}&{-1}\\ {9}&{-1} \end{pmatrix} \begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix} \label{5.20}\]
donde
\[A = \begin{pmatrix} {-1}&{-1}\\ {9}&{-1} \end{pmatrix}, \label{5.21}\]
Paso 1. Calcular los valores propios de A.
Los valores propios de A, denotan por\(\lambda\), están dados por las soluciones del polinomio característico:
\(det \begin{pmatrix} {-1-\lambda}&{-1}\\ {9}&{-1-\lambda} \end{pmatrix} = (-1-\lambda)^2+9 = 0\),
\[= \lambda^{2}+2\lambda+10 = 0, \label{5.22}\]
o
\(\lambda_{1,2} = -1 \pm \frac{1}{2}\sqrt{4-40} = -1 \pm 3i\)
Los vectores propios son complejos, por lo que sabemos que no es diagonalizable sobre los números reales. Lo que esto significa es que no podemos encontrar vectores propios reales para que pueda transformarse en una forma donde haya números reales en la diagonal, y ceros en las entradas fuera de la diagonal. Lo mejor que podemos hacer es transformarlo a una forma donde las partes reales del valor propio están en la diagonal, y las partes imaginarias están en las ubicaciones fuera de la diagonal, pero los elementos fuera de la diagonal difieren por un signo menos.
Paso 2. Calcular los vectores propios de A.
El vector propio de A correspondiente al vector propio\(-1-3i\) es la solución de las siguientes ecuaciones:
\[\begin{pmatrix} {-1}&{-1}\\ {9}&{-1} \end{pmatrix} \begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix} = (-1-3i) \begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix}, \label{5.23}\]
o
\[-x_{1}-x_{2} = -x_{1}-3ix_{2}, \label{5.24}\]
\[9x_{1}-x_{2} = -x_{2}-3ix_{2}. \label{5.25}\]
Una solución a estas ecuaciones viene dada por:
\(\begin{pmatrix} {1}\\ {3i} \end{pmatrix} = \begin{pmatrix} {1}\\ {0} \end{pmatrix}+i \begin{pmatrix} {0}\\ {3} \end{pmatrix}\)
Paso 3. Utilice los vectores propios de A para formar la matriz de transformación T.
Para la primera columna de T tomamos la parte real del vector propio correspondiente al valor propio\(-1-3i\), y para la segunda columna tomamos la parte compleja del vector propio:
\[T = \begin{pmatrix} {1}&{0}\\ {0}&{3} \end{pmatrix} \label{5.26}\]
con la inversa dada por:
\[T^{-1} = \begin{pmatrix} {1}&{0}\\ {0}&{\frac{1}{3}} \end{pmatrix} \label{5.27}\]
Paso 4. Cómputos\(\Lambda = T^{-1}AT\).
\(T^{-1}AT = \frac{1}{2}\begin{pmatrix} {1}&{0}\\ {0}&{\frac{1}{3}} \end{pmatrix} \begin{pmatrix} {-1}&{-1}\\ {9}&{-1} \end{pmatrix} \begin{pmatrix} {1}&{0}\\ {0}&{3} \end{pmatrix}\)
\(= \begin{pmatrix} {1}&{0}\\ {0}&{\frac{1}{3}} \end{pmatrix} \begin{pmatrix} {-1}&{-3}\\ {9}&{-3} \end{pmatrix}\)
\[= \begin{pmatrix} {-1}&{-3}\\ {3}&{-1} \end{pmatrix} \equiv \Lambda \label{5.28}\]
Con\(\Lambda\) esta forma, sabemos por el capítulo anterior que:
\[e^{\Lambda t} = e^{-t}\begin{pmatrix} {cos3t}&{-sin3t}\\ {sin3t}&{cos3t} \end{pmatrix} \label{5.29}\]
Entonces tenemos:
\(e^{At} = Te^{\Lambda t}T^{-1}\).
De esta expresión podemos concluir que\(e^{At} \rightarrow 0\) como\(t \rightarrow \infty\). De ahí que el origen sea asintóticamente estable. Se le conoce como sumidero y se caracteriza porque las partes reales de los valores propios de A son negativas. El plano de fase se esboza en la Fig. 5.2.
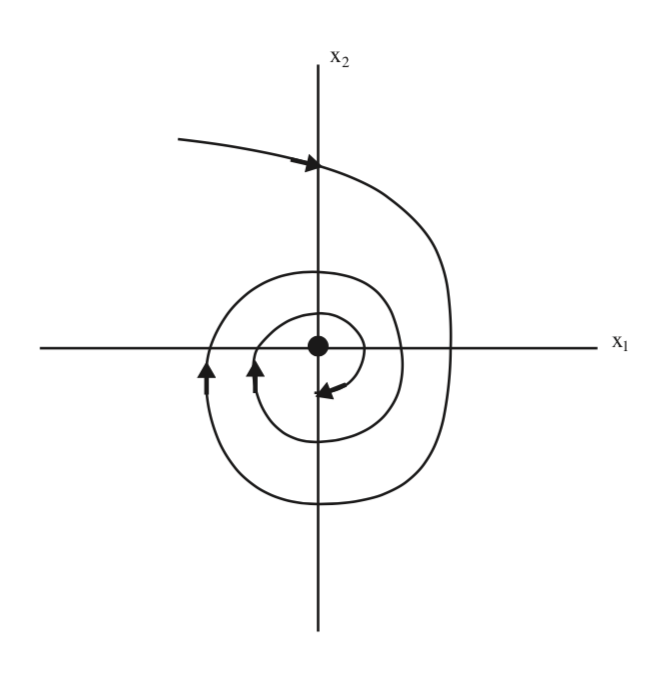
Ejemplo\(\PageIndex{12}\)
Consideramos la siguiente ODE lineal y autónoma:
\[\begin{pmatrix} {\dot{x_{1}}}\\ {\dot{x_{2}}} \end{pmatrix} = \begin{pmatrix} {-1}&{1}\\ {1}&{1} \end{pmatrix} \begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix} \label{5.30}\]
donde
\[A = \begin{pmatrix} {-1}&{1}\\ {1}&{1} \end{pmatrix}, \label{5.31}\]
Paso 1. Calcular los valores propios de A.
Los valores propios de A, denotan por\(\lambda\), están dados por las soluciones del polinomio característico:
\(det \begin{pmatrix} {-1-\lambda}&{1}\\ {1}&{1-\lambda} \end{pmatrix} = (-1-\lambda)(1-\lambda)-1 = 0\)
\[= \lambda^{2}-2 = 0, \label{5.32}\]
que son
\(\lambda_{1,2} = \pm\sqrt{2}\)
Paso 2. Calcular los vectores propios de A.
El autovector correspondiente al valor propio\(\sqrt{2}\) viene dado por la solución de las siguientes ecuaciones:
\[\begin{pmatrix} {-1}&{1}\\ {1}&{1} \end{pmatrix} \begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix} = \sqrt{2}\begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix}, \label{5.33}\]
o
\[-x_{1}+x_{2} = \sqrt{2}x_{1}, \label{5.34}\]
\[x_{1}+x_{2} = \sqrt{2}x_{2}. \label{5.35}\]
Una solución viene dada por:
\(x_{2} = (1+\sqrt{2})x_{1}\).
correspondiente al vector propio
\(\begin{pmatrix} {1}\\ {1+\sqrt{2}} \end{pmatrix}\)
El autovector correspondiente al valor propio\(-\sqrt{2}\) viene dado por la solución a las siguientes ecuaciones:
\[\begin{pmatrix} {-1}&{1}\\ {1}&{1} \end{pmatrix} \begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix} = -\sqrt{2}\begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix}, \label{5.36}\]
o
\[-x_{1}+x_{2} = -\sqrt{2}x_{1}, \label{5.37}\]
\[x_{1}+x_{2} = -\sqrt{2}x_{2}. \label{5.38}\]
Una solución viene dada por:
\(x_{2} = (1-\sqrt{2})x_{1}\).
correspondiente al vector propio:
\(\begin{pmatrix} {1}\\ {1-\sqrt{2}} \end{pmatrix}\)
Paso 3. Utilice los vectores propios de A para formar la matriz de transformación T.
Para las columnas de T tomamos los vectores propios correspondientes a los valores propios\(\sqrt{2}\) y\(-\sqrt{2}\):
\[T = \begin{pmatrix} {1}&{1}\\ {1+\sqrt{2}}&{1-\sqrt{2}} \end{pmatrix} \label{5.39}\]
con la inversa dada por:
\[T^{-1} = -\frac{1}{2\sqrt{2}}\begin{pmatrix} {1-\sqrt{2}}&{-1}\\ {-1-\sqrt{2}}&{1} \end{pmatrix} \label{5.40}\]
Paso 4. Cómputos\(\Lambda = T^{-1}AT\). Contamos con:
\(T^{-1}AT = -\frac{1}{2\sqrt{2}}\begin{pmatrix} {1-\sqrt{2}}&{-1}\\ {-1-\sqrt{2}}&{1} \end{pmatrix} \begin{pmatrix} {-1}&{1}\\ {1}&{1} \end{pmatrix} \begin{pmatrix} {1}&{1}\\ {1+\sqrt{2}}&{1-\sqrt{2}} \end{pmatrix}\)
\(= -\frac{1}{2\sqrt{2}}\begin{pmatrix} {1-\sqrt{2}}&{-1}\\ {-1-\sqrt{2}}&{1} \end{pmatrix} \begin{pmatrix} {\sqrt{2}}&{-\sqrt{2}}\\ {2+\sqrt{2}}&{2-\sqrt{2}} \end{pmatrix}\)
\[= \begin{pmatrix} {\sqrt{2}}&{0}\\ {0}&{-\sqrt{2}} \end{pmatrix} \equiv \Lambda \label{5.41}\]
Por lo tanto, en las\(u_{1}-u_{2}\) coordenadas (5.30) se convierte en:
\[\begin{pmatrix} {\dot{u_{1}}}\\ {\dot{u_{2}}} \end{pmatrix} = \begin{pmatrix} {\sqrt{2}}&{0}\\ {0}&{-\sqrt{2}} \end{pmatrix} \begin{pmatrix} {u_{1}}\\ {u_{2}} \end{pmatrix} \label{5.42}\]
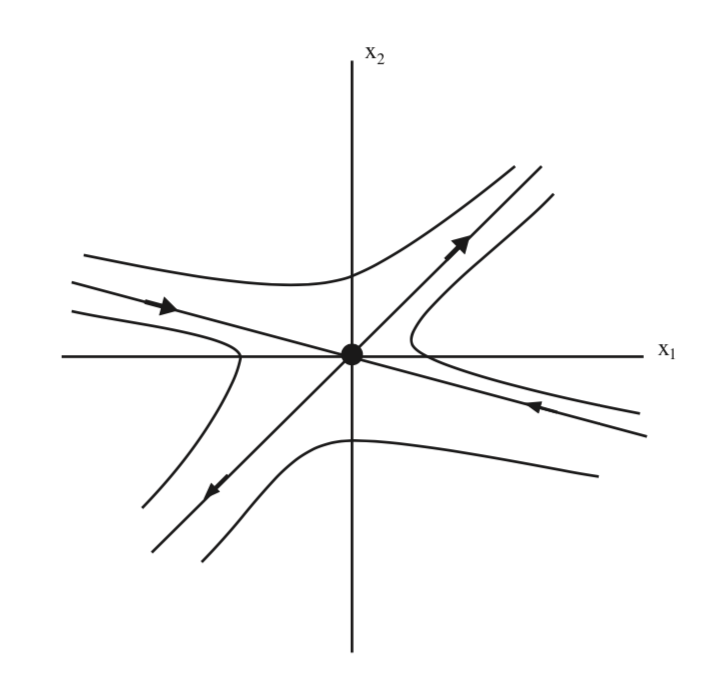
El retrato de fase de (5.42) se muestra en 5.3.
Es fácil ver que el origen es inestable para (5.42). En la fig. 5.3 vemos que el origen tiene la estructura de un punto de sillín, y queremos explorar más a fondo esta idea.
En las\(u_{1}-u_{2}\) coordenadas el lapso del vector propio correspondiente al valor propio viene dado por\(u_{2} = 0\),\(\sqrt{2}\) es decir, el\(u_{1}\) eje. El lapso del autovector correspondiente al valor propio viene dado por\(u_{1} = 0\),\(-\sqrt{2}\) es decir, el\(u_{2}\) eje. Además, podemos ver por la forma de (5.42) que estos ejes de coordenadas son invariantes. El\(u_{1}\) eje se conoce como el subespacio inestable, denotado por\(E^{u}\), y el\(u_{2}\) eje se conoce como el subespacio estable, denotado por\(E^{s}\). En otras palabras, el subespacio inestable es el lapso del autovector correspondiente al valor propio con parte real positiva y el subespacio estable es el lapso del vector propio correspondiente al valor propio que tiene parte real negativa. Los subespacios estables e inestables son subespacios invariantes con respecto al flujo generado por (5.42).
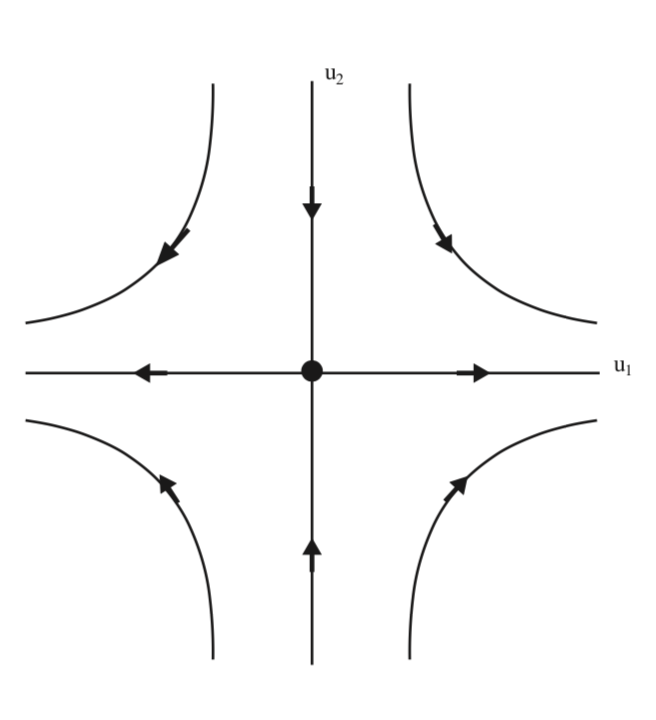
Los subespacios estables e inestables corresponden a los ejes de coordenadas del sistema de coordenadas dados por los vectores propios. A continuación queremos entender cómo aparecerían en las\(x_{1}-x_{2}\) coordenadas originales. Esto se logra transformándolas a las coordenadas originales usando la matriz de transformación (Ecuación\ ref {5.39}).
Primero transformamos el subespacio inestable de las\(u_{1}-u_{2}\) coordenadas a las\(x_{1}-x_{2}\) coordenadas. En las\(u_{1}-u_{2}\) coordenadas los puntos del subespacio inestable tienen coordenadas\((u_{1}, 0)\). Actuar sobre estos puntos con T da:
\[T\begin{pmatrix} {u_{1}}\\ {0} \end{pmatrix} = \begin{pmatrix} {1}&{1}\\ {1+\sqrt{2}}&{1-\sqrt{2}} \end{pmatrix} \begin{pmatrix} {u_{1}}\\ {0} \end{pmatrix} = \begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix}, \label{5.43}\]
que da la siguiente relación entre los puntos del subespacio inestable en las\(u_{1}-u_{2}\) coordenadas y los puntos en las\(x_{1}-x_{2}\) coordenadas:
\[u_{1} = x_{1}, \label{5.44}\]
\[(1+\sqrt{2})u_{1} = x_{2}, \label{5.45}\]
o
\[(1 + \sqrt{2})x_{1} = x_{2}. \label{5.46}\]
Esta es la ecuación para el subespacio inestable en las\(x_{1}-x_{2}\) coordenadas, que ilustramos en la Fig. 5.4.
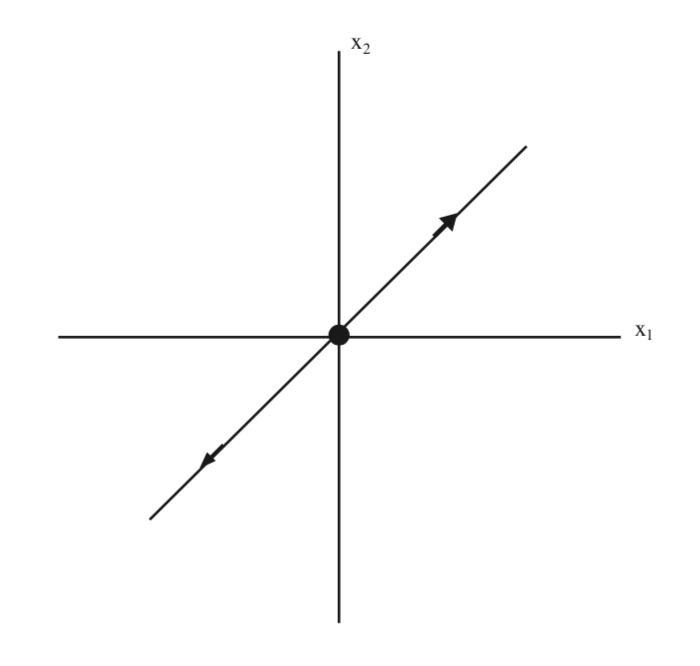
A continuación transformamos el subespacio estable de las\(u_{1}-u_{2}\) coordenadas a las\(x_{1}-x_{2}\) coordenadas. En las\(u_{1}-u_{2}\) coordenadas los puntos del subespacio estable tienen coordenadas\((0, u_{2})\). Actuar sobre estos puntos con T da:
\[T\begin{pmatrix} {0}\\ {u_{2}} \end{pmatrix} = \begin{pmatrix} {1}&{1}\\ {1+\sqrt{2}}&{1-\sqrt{2}} \end{pmatrix} \begin{pmatrix} {0}\\ {u_{2}} \end{pmatrix} = \begin{pmatrix} {x_{1}}\\ {x_{2}} \end{pmatrix}, \label{5.47}\]
que da la siguiente relación entre los puntos del subespacio estable en las\(u_{1}-u_{2}\) coordenadas y los puntos en las\(x_{1}-x_{2}\) coordenadas:
\[u_{2} = x_{1}, \label{5.48}\]
\[(1-\sqrt{2})u_{2} = x_{2}, \label{5.49}\]
o
\[(1-\sqrt{2})x_{1} = x_{2}. \label{5.50}\]
Esta es la ecuación para el subespacio estable en las\(x_{1}-x_{2}\) coordenadas, que ilustramos en la Fig. 5.5.
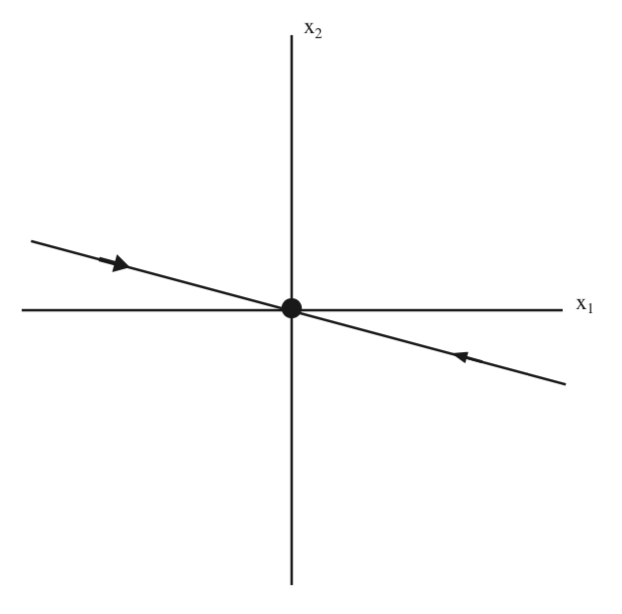
En la Fig. 5.6 ilustramos tanto los subespacios estables como los inestables en las coordenadas originales.
Ahora queremos discutir algunos resultados generales a partir de estos tres ejemplos.
Para los tres ejemplos, las partes reales de los valores propios de A fueron distintas de cero, y la estabilidad del origen se determinó por el signo de las partes reales de los valores propios, e.g., por ejemplo 10 el origen era inestable (las partes reales de los valores propios de A fueron positivas), por ejemplo 11 el origen fue estable (el partes reales de los valores propios de A fueron negativas), y por ejemplo 12 el origen fue inestable (A tuvo un valor propio positivo y un valor propio negativo). Esto es generalmente cierto para todos los campos vectoriales lineales y autónomos. Esto lo declaramos de manera más formal.
Considere un campo vectorial lineal y autónomo en\(\mathbb{R}^n\):
\[\dot{y} = Ay, y(0) = y_{0}, y \in \mathbb{R}^n. \label{5.51}\]
Entonces, si A no tiene valores propios que tienen cero partes reales, la estabilidad del origen viene determinada por las partes reales de los valores propios de A. Si todas las partes reales de los valores propios son estrictamente menores que cero, entonces el origen es asintóticamente estable. Si al menos uno de los valores propios de A tiene parte real estrictamente mayor que cero, entonces el origen es inestable.
Existe un término aplicado a esta terminología que impregna toda la teoría de sistemas dinámicos.
DEFINICIÓN 20: Punto de equilibrio hiperbólico
Se dice que el origen de la Ecuación\ ref {5.51} es si ninguna de las partes reales de los valores propios de A tiene cero partes reales.
De ello se deduce que los equilibrios hiperbólicos de campos vectoriales lineales y autónomos\(\mathbb{R}^n\) pueden ser sumideros, fuentes o sillas de montar. El punto clave es que todos los valores propios de A tienen partes reales distintas de cero.
Si nos limitamos a dos dimensiones, es posible hacer una (breve) lista de todas las formas canónicas distintas para A. Éstas vienen dadas por las siguientes seis\(2 \times 2\) matrices.
La primera es una matriz diagonal con valores propios reales distintos de cero, es decir\(\lambda, \mu \ne 0\), el origen es un punto fijo hiperbólico:
\[\begin{pmatrix} {\lambda}&{0}\\ {0}&{\mu} \end{pmatrix} \label{5.52}\]
En este caso el orgin puede ser un sumidero si ambos valores propios son negativos, una fuente si ambos valores propios son positivos, y un sillín si los valores propios tienen signo opuesto.
La siguiente situación corresponde a valores propios complejos, con la parte real,\(\alpha\), y la parte imaginaria\(\beta\), siendo ambas distintas de cero. En este caso el punto de equilibrio es hiperbólico, y\(\alpha\) hundirse para\(\alpha < 0\), y una fuente para\(\alpha > 0\). El signo de\(\beta\) no influye en la estabilidad:
\[\begin{pmatrix} {\alpha}&{\beta}\\ {\beta}&{-\alpha} \end{pmatrix} \label{5.53}\]
A continuación consideramos el caso cuando los valores propios son reales, idénticos y distintos de cero, pero la matriz no es diagonalizable, es decir, no se pueden encontrar dos vectores propios. En este caso el origen es hiperbólico para\(\lambda \ne 0\), y es un sumidero\(\lambda < 0\) y una fuente para\(\lambda > 0\):
\[\begin{pmatrix} {\lambda}&{1}\\ {0}&{\lambda} \end{pmatrix} \label{5.54}\]
A continuación consideramos que algunos casos correspondientes al origen son no hiperbólicos que habrían sido posibles incluir en la discusión de casos anteriores, pero es más instructivo señalar explícitamente estos casos por separado.
Primero consideramos el caso donde A es diagonalizable con un valor propio real distinto de cero y un valor propio cero:
\[\begin{pmatrix} {\lambda}&{0}\\ {0}&{0} \end{pmatrix} \label{5.55}\]
Consideramos el caso donde los dos valores propios son puramente imaginarios,\(\pm i\sqrt{b}\). En este caso el origen es ref! erró como centro.
\[\begin{pmatrix} {0}&{\beta}\\ {-\beta}&{0} \end{pmatrix} \label{5.56}\]
Para la completitud, consideramos el caso donde ambos valores propios son cero y A es diagonal.
\[\begin{pmatrix} {0}&{0}\\ {0}&{0} \end{pmatrix} \label{5.57}\]
Por último, queremos ampliar la discusión relacionada con los aspectos geométricos del Ejemplo 12. Recordemos que para ese ejemplo el lapso del vector propio correspondiente al valor propio con parte real negativa era un subespacio invariante, referido como el subespacio estable. Trayectorias con condiciones iniciales en el subespacio estable decayeron a cero a una velocidad exponencial como\(t \rightarrow +\infty\). El subespacio invariante estable fue denotado por\(E^s\). De igual manera, el lapso del vector propio correspondiente al valor propio con parte real positiva fue un subespacio invariante, denominado subespacio inestable. Trayectorias con condiciones iniciales en el subespacio inestable decayeron a cero a una velocidad exponencial como\(t \rightarrow -\infty\). El subespacio invariante inestable fue denotado por\(E^{u}\).
Podemos ver fácilmente que la Ecuación\ ref {5.52} tiene este comportamiento cuando\(\lambda\) y\(\mu\) tiene signos opuestos. Si\(\lambda\) y\(\mu\) son ambos negativos, entonces el lapso de los vectores propios correspondientes a estos dos valores propios es\(\mathbb{R}^2\), y todo el espacio de fase es el subespacio estable. Del mismo modo, si\(\lambda\) y\(\mu\) son ambos positivos, entonces el lapso de los vectores propios correspondientes a estos dos valores propios es\(\mathbb{R}^2\), y todo el espacio de fase es el subespacio inestable.
El caso Ecuación\ ref {5.53} es similar. Para ese caso no hay un par de vectores propios reales correspondientes a cada uno de los autovalores complejos. Los vectores que transforman la matriz original a esta forma canónica se denominan vectores propios generalizados. Si\(\alpha < 0\) el lapso de los vectores propios generalizados es\(\mathbb{R}^2\), y todo el espacio de fase es el subespacio estable. Del mismo modo, si\(\alpha > 0\) el lapso de los vectores propios generalizados es\(\mathbb{R}^2\), y todo el espacio de fase es el subespacio inestable. La situación es similar para (5.54). Para todo\(\lambda < 0\) el espacio de fase es el subespacio estable, para todo\(\lambda > 0\) el espacio de fase es el subespacio inestable.
El caso en la Ecuación\ ref {5.55} es diferente. El lapso del autovector correspondiente a\(\lambda\) es el subespacio estable para\(\lambda < 0\), y el subespacio inestable para\(\lambda > 0\) El espacio del autovector correspondiente al valor propio cero se conoce como el subespacio central.
Para el caso (5.56) no hay dos vectores propios reales que conduzcan a la forma canónica resultante. Más bien, hay dos vectores propios generalizados asociados a este par de valores propios complejos que tienen una parte real cero. El lapso de estos dos vectores propios es un subespacio central bidimensional correspondiente a\(\mathbb{R}^2\). Un punto de equilibrio con valores propios puramente imaginarios se denomina centro.
Finalmente, se incluye el caso en la Ecuación\ ref {5.57} para su integridad. Es el campo vectorial cero donde\(\mathbb{R}^2\) está el subespacio central.
Podemos caracterizar la estabilidad del origen en términos de los subespacios estables, inestables y centrales. El origen es asintóticamente estable si\(E^u = \emptyset\) y\(E^c = \emptyset\) .El origen es inestable si\(E^u \ne \emptyset\).


