6: Colectores de Equilibrios Estables e Inestables
- Page ID
- 113587
Para equilibrios hiperbólicos de campos vectoriales autónomos, la linealización captura el comportamiento local cerca de los equilibrios para el campo vectorial no lineal. Se describen los resultados que justifican esta afirmación en el contexto de los sistemas autónomos bidimensionales.
Consideramos un\(C^r\) campo vectorial autónomo\(r \ge 1\) bidimensional de la siguiente forma:
\(\dot{x} = f(x,y)\),
\[\dot{y} = g(x, y), (x, y) \in \mathbb{R}^2. \label{6.1}\]
Dejar\(\phi_{t}(\cdot)\) denotar el flujo generado por (6.1). Supongamos que\((x_{0}, y_{0})\) es un punto de equilibrio hiperbólico de este campo vectorial, es decir, los dos valores propios de la matriz jacobiana:
\(\begin{pmatrix} {\frac{\partial f}{\partial x}(x_{0},y_{0})}&{\frac{\partial f}{\partial y}(x_{0},y_{0})}\\ {\frac{\partial g}{\partial x}(x_{0},y_{0})}&{\frac{\partial g}{\partial y}(x_{0},y_{0})} \end{pmatrix}\)
- \((x_{0}, y_{0})\)es una fuente para el campo vectorial linealizado,
- \((x_{0}, y_{0})\)es un sumidero para el campo vectorial linealizado,
- \((x_{0}, y_{0})\)es un sillín para el campo vectorial linealizado.
Consideramos cada caso individualmente.
- En este caso\((x_{0}, y_{0})\) es una fuente para (6.1). Más precisamente, existe un barrio U de\((x_{0}, y_{0})\) tal manera que para cualquier\(p \in U\),\(\phi_{t}(p)\) deja U a medida que t aumenta.
- En este caso\((x_{0}, y_{0})\) es un fregadero para (6.1). Más precisamente, existe una vecindad S de\((x_{0}, y_{0})\) tal manera que para cualquiera\(p \in S\),\(\phi_{t}(p)\) se acerca\((x_{0}, y_{0})\) a un ritmo exponencial a medida que t aumenta. En este caso\((x_{0}, y_{0})\) es un ejemplo de un conjunto atrayente y su cuenca de atracción viene dada por:
\(B \equiv \bigcup_{t \le 0} \phi_{t}(S).\)
- Para el caso de los puntos de sillín hiperbólicos, la estructura del punto de sillín aún se mantiene cerca del punto de equilibrio para sistemas no lineales. Ahora explicamos precisamente lo que esto significa. Para ello tendremos que examinar (6.1) más de cerca. En particular, necesitaremos transformar (6.1) a un sistema de coordenadas que “localice” el comportamiento cerca del punto de equilibrio y muestre específicamente la estructura de la parte lineal. Ya lo hemos hecho varias veces al examinar el comportamiento cerca de soluciones específicas, por lo que no vamos a repetir esos detalles.
Transformando localmente cerca\((x_{0}, y_{0})\) de esta manera, podemos expresar (6.1) en la siguiente forma:
\[\begin{pmatrix} {\dot{\zeta}}\\ {\dot{\eta}} \end{pmatrix} = \begin{pmatrix} {-\alpha}&{0}\\ {0}&{\beta} \end{pmatrix} \begin{pmatrix} {\zeta}\\ {\eta} \end{pmatrix}+ \begin{pmatrix} {u(\zeta, \eta)}\\ {v(\zeta, \eta)} \end{pmatrix}, \alpha, \beta > 0, (\zeta, \eta) \in \mathbb{R}^2, \label{6.2}\]
donde el jacobiano en su origen,
\[\begin{pmatrix} {-\alpha}&{0}\\ {0}&{\beta} \end{pmatrix}, \label{6.3}\]
refleja la naturaleza hiperbólica del punto de equilibrio. La linealización de (6.1) sobre el origen viene dada por:
\[\begin{pmatrix} {\dot{\zeta}}\\ {\dot{\eta}} \end{pmatrix} = \begin{pmatrix} {-\alpha}&{0}\\ {0}&{\beta} \end{pmatrix} \begin{pmatrix} {\zeta}\\ {\eta} \end{pmatrix}, \label{6.4}\]
Es fácil de ver para el sistema linealizado que
\[E^s = {(\zeta, \eta)|\eta = 0}, \label{6.5}\]
es el subespacio estable invariante y
\[E^u = {(\zeta, \eta)|\zeta = 0}, \label{6.6}\]
es el subespacio inestable invariante.
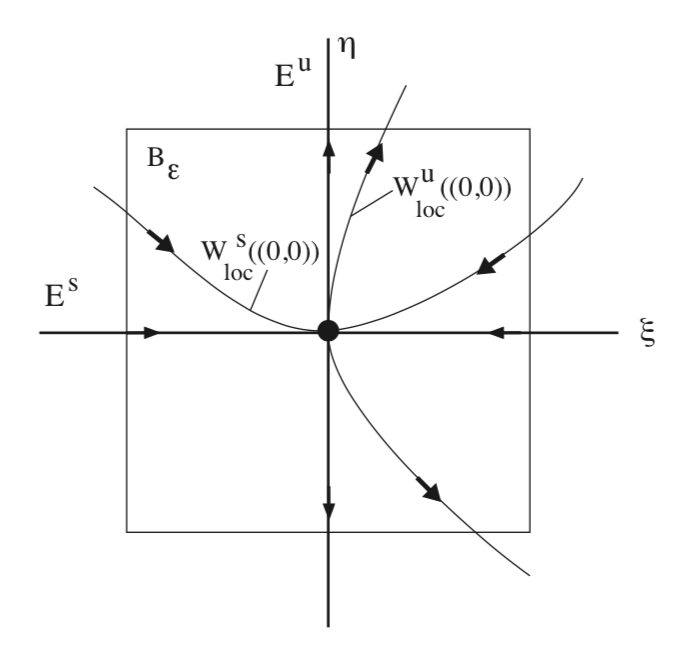
Ahora exponemos cómo esta estructura de punto de silla de montar es heredada por el sistema no lineal al afirmar los resultados del teorema del colector estable e inestable para los equilibrios hiperbólicos para campos vectoriales no autónomos bidimensionales.
Primero, consideramos dos intervalos de los ejes de coordenadas que contienen el origen de la siguiente manera:
\[I_{\zeta} \equiv {-\epsilon < \zeta < \epsilon}, \label{6.7}\]
y
\[I_{\eta} \equiv {-\epsilon < \eta < \epsilon}, \label{6.8}\]
para algunos pequeños\(\epsilon > 0\). Un barrio del origen se construye tomando el producto cartesiano de estos dos intervalos:
\[B_{\epsilon} \equiv \{(\zeta, \eta) \in \mathbb{R}^2|(\zeta, \eta) \in I_{\zeta} \times I_{\eta}\}, \label{6.9}\]
y se ilustra en la Fig. 6.1. El teorema del colector estable e inestable para los puntos de equilibrio hiperbólico de los campos vectoriales autónomos establece lo siguiente.
Existe una\(C^r\) curva, dada por la gráfica de una función de las\(\zeta\) variables:
\[\eta = S(\zeta), \zeta \in I_{\zeta}, \label{6.10}\]
Esta curva tiene tres propiedades importantes.
Pasa por el origen, es decir, S (0) = 0.
Es tangente a\(E^s\) en el origen, es decir,\(\frac{dS}{d\zeta} (0) = 0\).
Es localmente invariante en el sentido de que cualquier trayectoria que comience en la curva se acerca al origen a una tasa exponencial como\(t \rightarrow \infty\), y deja\(B_{\epsilon}\) como\(t \rightarrow -\infty\).
Además, la curva que satisface estas tres propiedades es única. Por estas razones, esta curva es referida como el colector local estable del origen, y se denota por:
\[W_{loc}^{s}((0, 0)) = \{(\zeta, \eta) \in B_{\epsilon}|\eta = S(\zeta)\}. \label{6.11}\]
De igual manera, existe otra\(C^{r}\) curva, dada por la gráfica de una función de las\(\eta\) variables:
\[\zeta = U(\eta), \eta \in I_{\eta}, \label{6.12}\]
Esta curva tiene tres propiedades importantes.
Pasa por el origen, es decir, U (0) = 0.
Es tangente a\(E^u\) en el origen, es decir,\(\frac{dU}{d\eta} (0) = 0\).
Es localmente invariante en el sentido de que cualquier trayectoria que comience en la curva se acerca al origen a una tasa exponencial como\(t \rightarrow -\infty\), y deja\(B_{\epsilon}\) como\(t \rightarrow \infty\).
Por estas razones, esta curva es referida como el colector inestable local del origen, y se denota por:
\[W_{loc}^{u}((0, 0)) = \{(\zeta, \eta) \in B_{\epsilon}|\zeta = S(\zeta)\}. \label{6.13}\]
La curva que satisface estas tres propiedades es única.
Estos colectores locales estables e inestables son las “semillas” para los colectores globales estables e inestables que se definen de la siguiente manera:
\[W^{s} ((0, 0)) \equiv \bigcup_{t \le 0} \phi_{t}(W_{loc}^{s}((0, 0))), \label{6.14}\]
y
\[W^{u} ((0, 0)) \equiv \bigcup_{t \ge 0} \phi_{t}(W_{loc}^{u}((0, 0))), \label{6.15}\]
Ahora consideraremos una serie de ejemplos que muestran cómo se utilizan estas ideas.
Ejemplo\(\PageIndex{13}\)
Consideramos el siguiente campo vectorial autónomo y no lineal en el plano:
\(\dot{x} = x\),
\[\dot{y} = y + x^2, (x, y) \in \mathbb{R}^2. \label{6.16}\]
Este campo vectorial tiene un punto de equilibrio en el origen, (x, y) = (0, 0). El jacobiano del campo vectorial evaluado en el origen viene dado por:
\[\begin{pmatrix} {1}&{0}\\ {0}&{-1} \end{pmatrix}. \label{6.17}\]
De este cálculo podemos concluir que el origen es un punto de sillín hiperbólico. Además, el eje x es el subespacio inestable para el campo vectorial linealizado y el eje y es el subespacio estable para el campo vectorial linealizado.
A continuación consideramos el campo vectorial no lineal (6.16). Por inspección, vemos que el eje y (i.e. x = 0) es el colector estable global para el origen. A continuación consideramos el colector inestable. Dividiendo la segunda ecuación por la primera ecuación en (6.16) da:
\[\frac{\dot{y}}{\dot{x}} = \frac{dy}{dx} = -\frac{y}{x} + x. \label{6.18}\]
Esta es una ecuación lineal no autónoma. Una solución de esta ecuación que pasa por el origen viene dada por:
\[y = \frac{x^2}{3}, \label{6.19}\]
También es tangente al subespacio inestable en el origen. Es el colector inestable global.
Examinamos más a fondo esta afirmación. Es fácil calcular el flujo generado por (6.16). El componente x puede resolverse y sustituirse en el componente y para producir una ecuación lineal no autónoma de primer orden. Por lo tanto, el flujo generado por (6.16) viene dado por:
\(x(t, x_{0}) = x_{0}e^t\),
\[y(t, t_{0}) = (y_{0}-\frac{x_{0}^2}{3})e^{-t}+\frac{x_{0}^2}{3}e^{2t}, \label{6.20}\]
El múltiple inestable global del origen es el conjunto de condiciones iniciales que tienen la propiedad de que las trayectorias a través de estas condiciones iniciales se acercan al origen a una tasa exponencial como\(t \rightarrow -\infty\). Al examinar los dos componentes de (6.20), vemos que el componente x se acerca a cero como\(t \rightarrow -\infty\) para cualquier elección de\(x_{0}\). Sin embargo, el componente y solo se acercará a cero como\(t \rightarrow -\infty\) si\(y_{0}\) y\(x_{0}\) se eligieran de tal manera que
\[y_{0} = \frac{x_{0}^2}{3}, \label{6.21}\]
De ahí que (6.21) sea el múltiple inestable global del origen.
Ejemplo\(\PageIndex{14}\)
Considere el siguiente campo vectorial autónomo no lineal en el plano:
\(\dot{x} = x-x^3\),
\[\dot{y} = -y, (x, y) \in \mathbb{R}^2. \label{6.22}\]
Tenga en cuenta que los componentes x e y evolucionan de forma independiente.
Los puntos de equilibrio y los jacobianos asociados con sus linealizaciones se dan de la siguiente manera:
\[(x, y) = (0, 0); \begin{pmatrix} {1}&{0}\\ {0}&{-1} \end{pmatrix}; saddle \label{6.23}\]
\[(x, y) = (\pm 1, 0); \begin{pmatrix} {-2}&{0}\\ {0}&{-1} \end{pmatrix}; sinks \label{6.24}\]
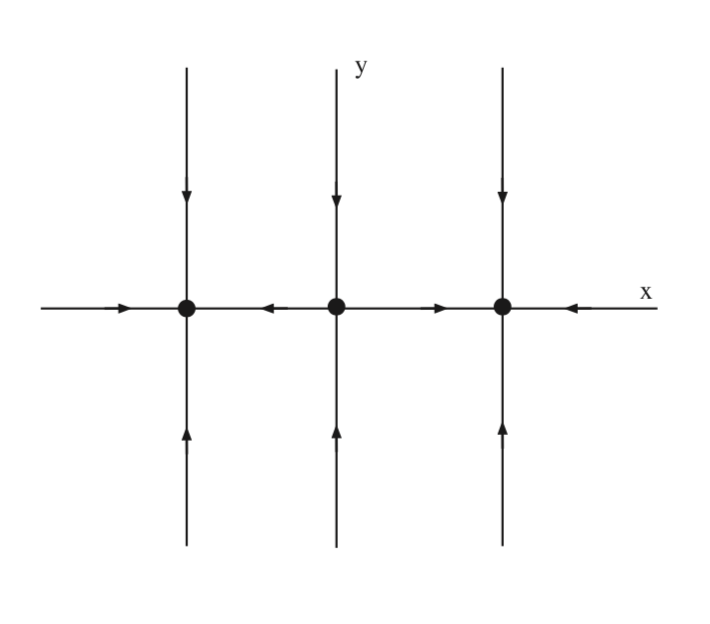
Ahora calculamos los colectores globales estables e inestables de estos equilibrios. Comenzamos con el punto de sillín en el origen.
\(W^{s} ((0, 0)) = \{(x, y)|x = 0\}\)
\[W^{u} ((0, 0)) = \{(x, y)|-1 < x < 1, y = 0\} \label{6.25}\]
Para los sumideros, el colector estable global es sinónimo de la cuenca de atracción para el fregadero.
\[(1, 0): W^{s} ((1, 0)) = \{(x, y)|x > 0\} \label{6.26}\]
\[(-1, 0): W^{s} ((-1, 0)) = \{(x, y)|x < 0\} \label{6.27}\]
Ejemplo\(\PageIndex{15}\)
En este ejemplo consideramos el siguiente campo vectorial autónomo no lineal en el plano:
\(\dot{x} = -x\),
\[\dot{y} = y^{2}(1-y^{2}), (x, y) \in \mathbb{R}^2. \label{6.28}\]
Tenga en cuenta que los componentes x e y evolucionan de forma independiente.
Los puntos de equilibrio y los jacobianos asociados con sus linealizaciones se dan de la siguiente manera:
\[(x, y) = (0, 0), (0, \pm 1) \label{6.29}\]
\[(x, y) = (0, 0); \begin{pmatrix} {-1}&{0}\\ {0}&{0} \end{pmatrix}; not hyperbolic \label{6.30}\]
\[(x, y) = (0, 1); \begin{pmatrix} {-1}&{0}\\ {0}&{-2} \end{pmatrix}; sink \label{6.31}\]
\[(x, y) = (0, -1); \begin{pmatrix} {-1}&{0}\\ {0}&{2} \end{pmatrix}; saddle \label{6.32}\]
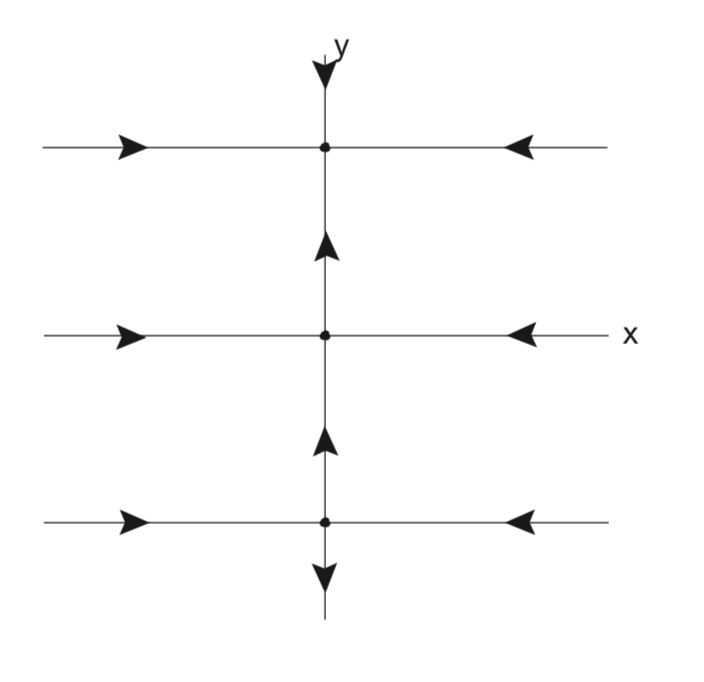
Ahora calculamos la estructura múltiple invariante global para cada uno de los equilibrios, comenzando con (0, 0).
\(W^{s} ((0, 0)) = \{(x, y)|y = 0\}\)
\[W^{u} ((0, 0)) = \{(x, y)|-1 < y < 1, x = 0\} \label{6.33}\]
El eje x es claramente el colector estable global para este punto de equilibrio. El segmento en el eje\(-1\) y entre y 1 es invariante, pero no corresponde a una dirección hiperbólica. Se le conoce como el colector central del origen, y más adelante aprenderemos mucho más sobre los colectores invariantes asociados con direcciones no hiperbólicas.
El punto de equilibrio (0, 1) es un sumidero. Su colector global estable (cuenca de atracción) viene dado por:
\[W^{s} ((0, 1)) = \{(x, y)|y > 0\} \label{6.34}\]
El punto de equilibrio\((0, -1)\) es un punto de sillín con colectores globales estables e inestables dados por:
\(W^{s} ((0, -1)) = \{(x, y)|y = -1\}\)
\[W^{u} ((0, -1)) = \{(x, y)|-\infty < y < 0, x = 0\} \label{6.35}\]
Ejemplo\(\PageIndex{16}\)
En este ejemplo consideramos el siguiente campo vectorial autónomo no lineal en el plano:
\(\dot{x} = y\),
\[\dot{y} = x-x^{3}-\delta y, (x, y) \in \mathbb{R}^2, \delta > 0, \label{6.36}\]
donde\(\delta > 0\) se va a ver como un parámetro. Los puntos de equilibrio vienen dados por:
\[(x, y) = (0, 0), (\pm 1, 0). \label{6.37}\]
Queremos clasificar la estabilidad linealizada de los equilibrios. El jacobiano del campo vectorial viene dado por:
\[A = \begin{pmatrix} {0}&{1}\\ {1-3x^2}&{-\delta} \end{pmatrix}, \label{6.38}\]
y los valores propios del jacobiano son:
\[\lambda_{\pm} = -\frac{\delta}{2} \pm \frac{1}{2}\sqrt{\delta^2+4-12x^2}. \label{6.39}\]
Evaluamos esta expresión para los valores propios en cada uno de los equilibrios para determinar su estabilidad linealizada.
\[(0, 0); \lambda_{\pm} = -\frac{\delta}{2} \pm \frac{1}{2}\sqrt{\delta^2+4} \label{6.40}\]
Tenga en cuenta que
\(\delta^2+4 > \delta^2\)
por lo tanto los valores propios son siempre reales y de signo opuesto. Esto implica que (0, 0) es una silla de montar.
\[(\pm 1, 0); \lambda_{\pm} = -\frac{\delta}{2} \pm \frac{1}{2}\sqrt{\delta^2-8} \label{6.41}\]
Primero, tenga en cuenta que
\(\delta^2-8 < \delta^2\).
Esto implica que estos dos puntos fijos son siempre sumideros. Sin embargo, hay dos subcasos.
\(\delta^2-8 < 0\): Los valores propios tienen una parte imaginaria distinta de cero.
\(\delta^2-8 > 0\): Los valores propios son puramente reales.
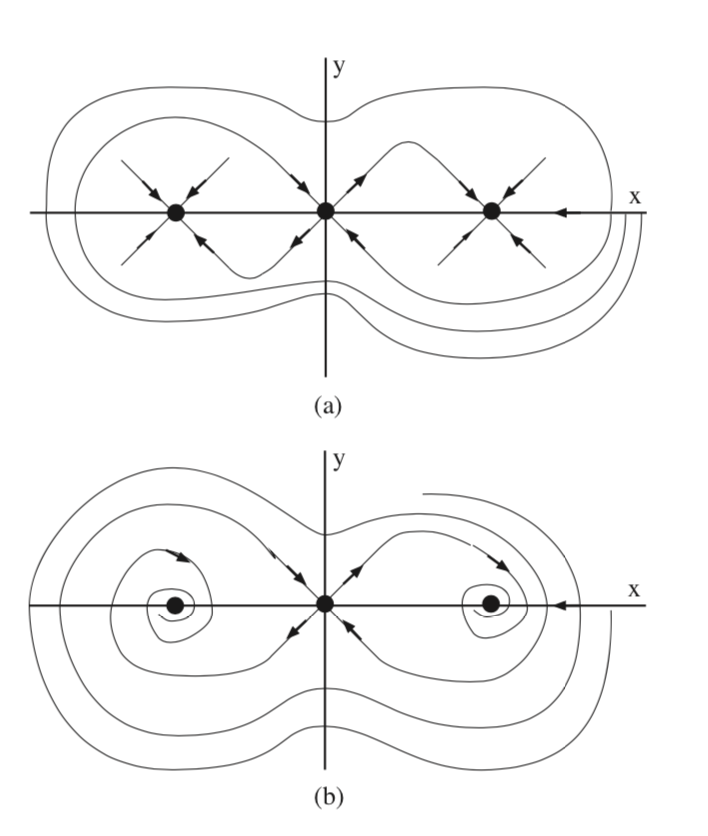
En la fig. 6.4 se esboza la estructura del colector invariante local para estos dos casos.
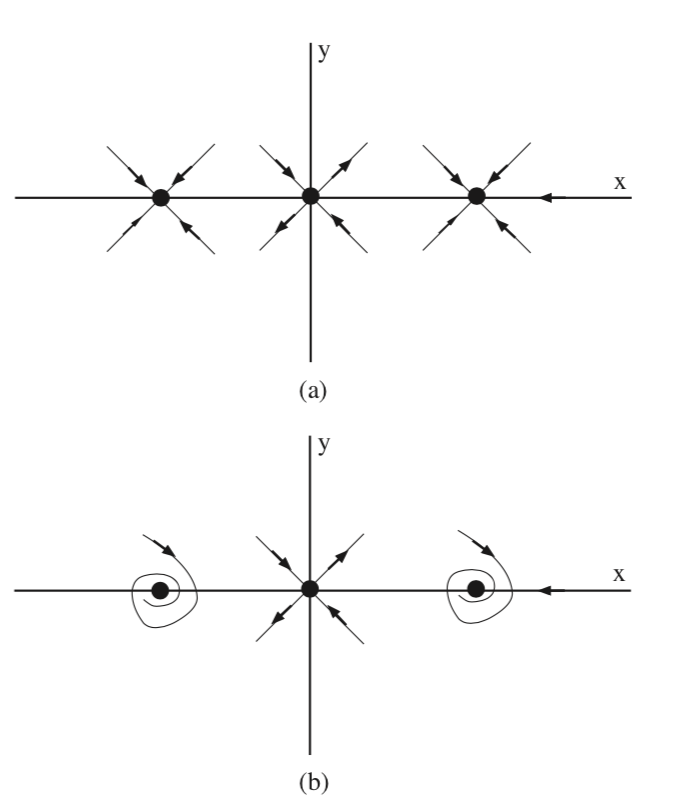
En la fig. 6.5 se esboza la estructura global del colector invariante para los dos casos. En las próximas conferencias aprenderemos cómo podemos justificar esta cifra. Sin embargo, tenga en cuenta el papel que juega el colector estable de la silla de montar en la definición de las cuencas de atracciones de los dos sumideros.