1.4: Líneas, planos e hiperplanos

En esta sección vamos a añadir a nuestra comprensión geométrica básica de\(\mathbb{R}^n\) mediante el estudio de líneas y planos. Si lo hacemos con cuidado, veremos que trabajar con líneas y planos en no\(\mathbb{R}^n\) es más difícil que trabajar con ellos en\(\mathbb{R}^2\) o\(\mathbb{R}^3\).

Líneas en\(\mathbb{R}^n\)

Empezaremos con líneas. Recordemos de la Sección 1.1 que si\(\mathbf{v}\) es un vector distinto de cero en\(\mathbb{R}^n\), entonces, para cualquier escalar\(t\),\(t \mathbf{v}\) tiene la misma dirección que\(\mathbf{v}\) cuando\(t>0\) y la dirección opuesta cuando\(t < 0\). De ahí el conjunto de puntos

\[ \{ t\mathbf{v}:-\infty<t<\infty \} \nonumber \]

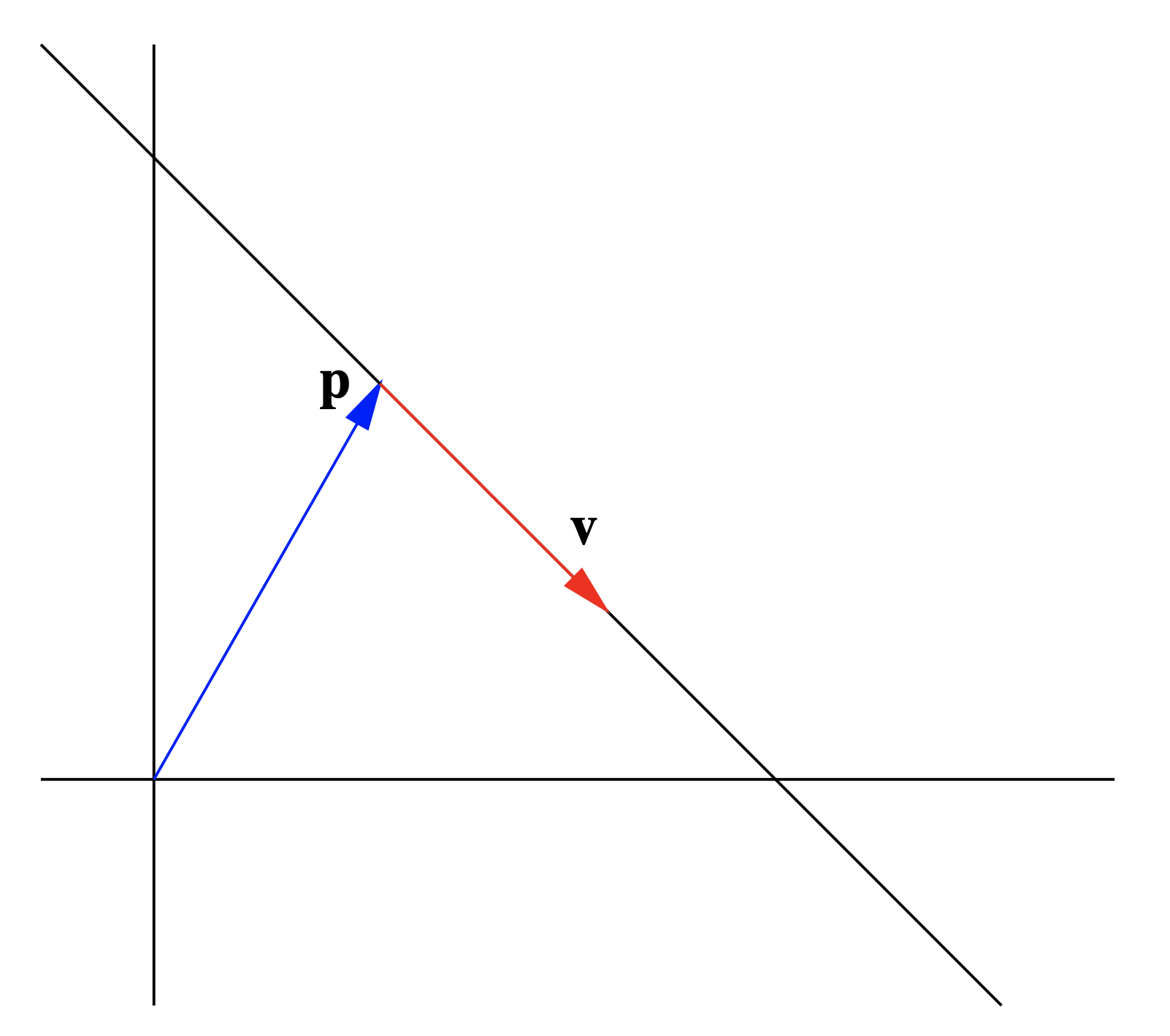
forma una línea a través del origen. Si ahora agregamos un vector\(\mathbf{p}\) a cada uno de estos puntos, obtenemos el conjunto de puntos

\[ \{t\mathbf{v}+\mathbf{p}:-\infty<t<\infty \}, \nonumber \]

que es una línea a través\(\mathbf{p}\) en la dirección de\(\mathbf{v}\), como se ilustra en la Figura 1.4.1 para\(\mathbb{R}^2\).

Figura\(\PageIndex{}\):\ PageIndex {1}\): Una\(\mathbb{R}^2\) línea\(\mathbf{p}\) en la dirección de\(\mathbf{v}\)

Definición\(\PageIndex{1}\)

Dado un vector\(\mathbf{p}\) y un vector distinto de cero\(\mathbf{v}\) en\(\mathbb{R}^n\), el conjunto de todos los puntos\(\mathbf{y}\) en\(\mathbb{R}^n\) tal que

\[ \mathbf{y}=t \mathbf{v}+\mathbf{p}, \label{1.4.1} \]

donde\(-\infty<t<\infty\), se llama la línea a través\(\mathbf{p}\) en la dirección de\(\mathbf{v}\).

La ecuación (\(\ref{1.4.1}\)) se denomina ecuación vectorial para la línea. Si escribimos\(\mathbf{y}=\left(y_{1}, y_{2}, \ldots, y_{n}\right)\),\(\mathbf{v}=\left(v_{1}, v_{2}, \ldots, v_{n}\right)\), y\(\mathbf{p}=\left(p_{1}, p_{2}, \ldots, p_{n}\right)\), entonces (1.4.1) puede escribirse como

\[\left(y_{1}, y_{2}, \ldots, y_{n}\right)=t\left(v_{1}, v_{2}, \ldots, v_{n}\right)+\left(p_{1}, p_{2}, \ldots, p_{n}\right) , \label{1.4.2} \]

que se mantiene si y solo si

\ [\ begin {align}
&y_ {1} =t v_ {1} +p_ {1},\ nonumber\\
&y_ {2} =t v_ {2} +p_ {2},\ label {1.4.3}\\
&\ vdots\ nonumber\\
&y_ {n} =t v_ {n} +p_ {n} +p_ {n}. \ nonumber
\ end {align}\]

Las ecuaciones en (\(\ref{1.4.3}\)) se denominan ecuaciones paramétricas para la línea.

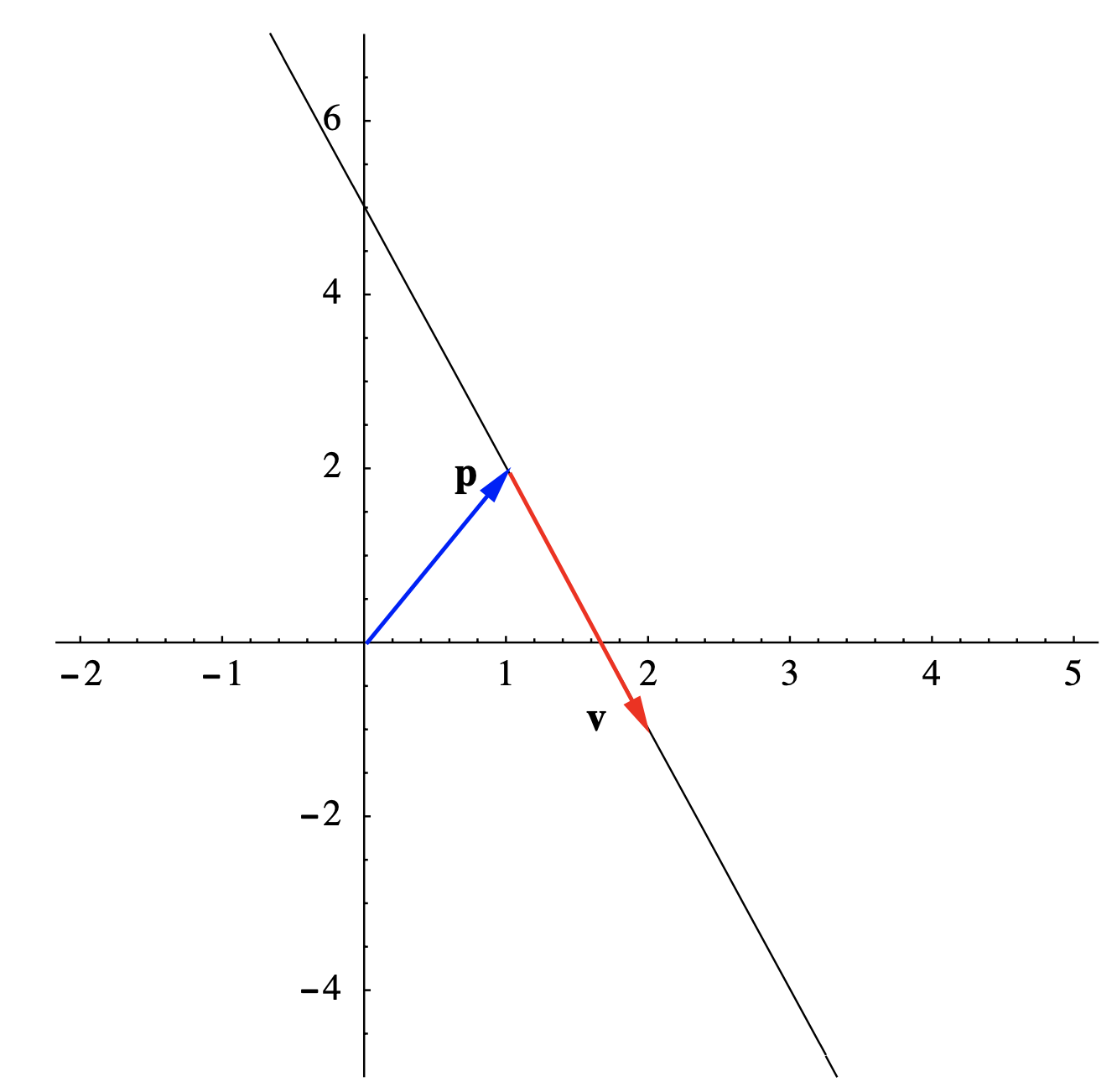
Ejemplo\(\PageIndex{1}\)

Supongamos que\(L\) es la línea que\(\mathbf{p}=(1,2)\) entra\(\mathbb{R}^2\) a través en la dirección de\(\mathbf{v}=(1,-3)\) (ver Figura 1.4.2). Entonces

\[\mathbf{y}=t(1,-3)+(1,2)=(t+1,-3 t+2) \nonumber \]

es una ecuación vectorial para\(L\) y, si lo dejamos\( \mathbf{y}=(x, y)\),

\ [\ begin {alineado}
&x=t+1,\\
&y=-3 t+2
\ end {alineado}\]

son ecuaciones paramétricas para\(L\). Tenga en cuenta que si resolvemos para\(t\) en ambas ecuaciones, tenemos

\ [\ begin {alineado}
t &=x-1\\
t &=\ frac {2-y} {3}.
\ end {alineado}\]

Así

\[x-1=\frac{2-y}{3} , \nonumber \]

y así

\[y=-3 x+5 . \nonumber \]

Por supuesto, esta última es solo la forma estándar de pendiente-intercepción para la ecuación de una línea en\(\mathbb{R}^2\).

Figura\(\PageIndex{}\):\ PageIndex {2}\): La línea a través\(\mathbf{p} = (1,2) \) en la dirección de\(\mathbf{v} =(1,-3)\)

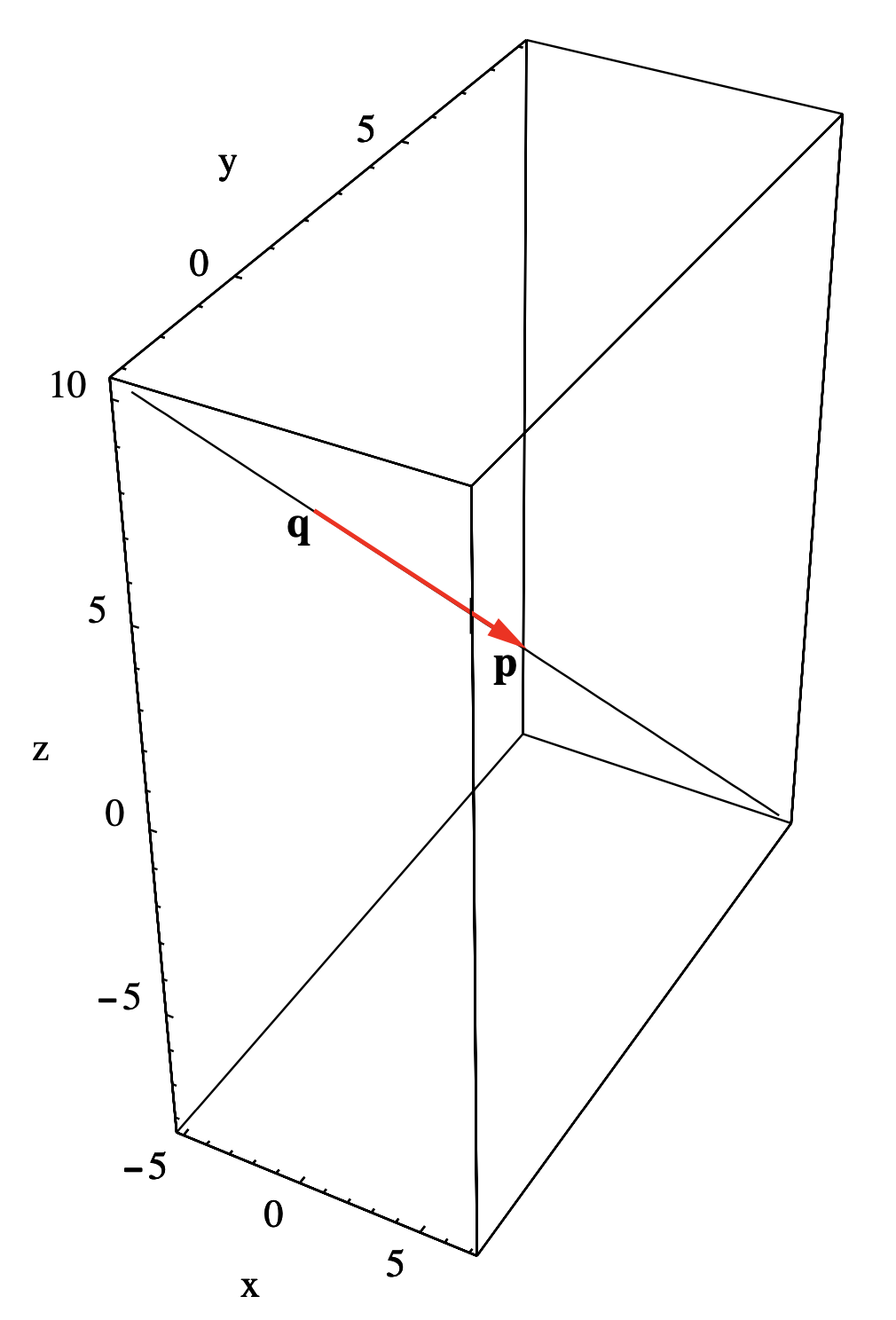
Ejemplo\(\PageIndex{2}\)

Ahora supongamos que deseamos encontrar una ecuación para la línea L en la\(\mathbb{R}^3\) que pasa por los puntos\(\mathbf{p}=(1,3,1)\) y\(\mathbf{q}=(-1,1,4)\) (ver Figura 1.4.3). Primero notamos que el vector

\[\mathbf{p}-\mathbf{q}=(2,2,-3) \nonumber \]

da la dirección de la línea, por lo que

\[\mathbf{y}=t(2,2,-3)+(1,3,1) \nonumber \]

es una ecuación vectorial para\(L\); si lo dejamos\(\mathbf{y}=(x, y, z)\),

\ [\ begin {alineado}
&x=2 t+1,\\
&y=2 t+3,\\
&z=-3 t+1
\ end {alineado}\]

son ecuaciones paramétricas para\(L\).

Figura\(\PageIndex{}\):\ PageIndex {3}\): La línea a través\(\mathbf{p}=(1,3,1)\) y\(\mathbf{q}=(-1,1,4)\)

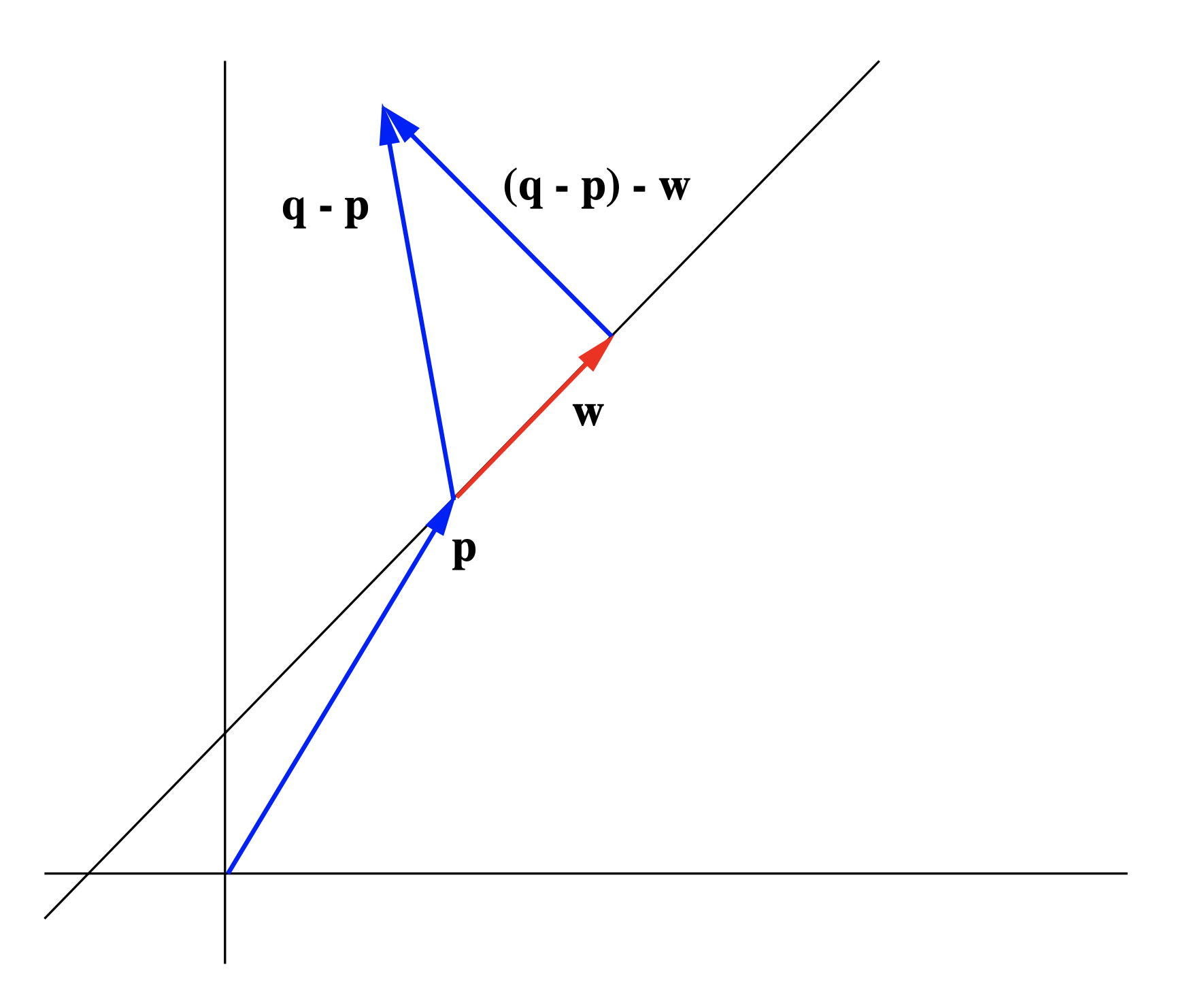
Como aplicación de estas ideas, considere el problema de encontrar la distancia más corta desde un punto\( \mathbf{q}\) \(\mathbb{R}^n\)hasta una línea L con ecuación\(\mathbf{y}=t \mathbf{v}+\mathbf{p}\). Si dejamos\( \mathbf{w}\) ser la proyección de\(\mathbf{q}-\mathbf{p}\) sobre\( \mathbf{v}\), entonces, como vimos en la Sección 1.2, el vector\((\mathbf{q}-\mathbf{p})-\mathbf{w}\) es ortogonal\(\mathbf{v}\) y puede ser representado con su cola puesta\(L\) y su punta en\(\mathbf{q}\). De ahí que la distancia más corta de\(\mathbf{q}\) a\(L\) sea\(\|(\mathbf{q}- \mathbf{p}) − \mathbf{w}\|\). Ver Figura 1.4.4.

Figura\(\PageIndex{}\):\ PageIndex {4}\): Distancia de un punto\( \mathbf{q}\) a una línea

Ejemplo\(\PageIndex{3}\)

Para encontrar la distancia desde el punto\(\mathbf{q}=(2,2,4)\) hasta la línea\(L\) a través de los puntos\(\mathbf{p}=(1,0,0)\) y\(\mathbf{r}=(0,1,0)\), primero debemos encontrar una ecuación para\(L\). Dado que la dirección de\(L\) está dada por\(\mathbf{v}=\mathbf{r}-\mathbf{p}=(-1,1,0)\), una ecuación vectorial para\(L\) es

\[\mathbf{y}=t(-1,1,0)+(1,0,0) . \nonumber \]

Si dejamos

\[ \mathbf{u}=\frac{\mathbf{v}}{\|\mathbf{v}\|}=\frac{1}{\sqrt{2}}(-1,1,0) , \nonumber \]

entonces la proyección de\(\mathbf{q}-\mathbf{p}\) sobre\(\mathbf{v}\) es

\ [\ begin {ecuación}
\ izquierda. \ mathbf {w} = ((\ mathbf {q} -\ mathbf {p})\ cdot\ mathbf {u})\ mathbf {u} =\ izquierda ((1,2,4)\ cdot\ frac {1} {\ sqrt {2}} (-1,1,0)\ derecha)\ derecha)\ frac {1} {\ sqrt {2}} (-1,1,0)\ derecha)\ frac {1} {\ sqrt {2}} (-1,1,0) 0) =\ frac {1} {2} (-1,1,0).
\ end {ecuación}\ nonumber\]

Por lo tanto, la distancia de\(\mathbf{q}\) a\(L\) es

\ [\ begin {ecuación}
\ | (\ mathbf {q} -\ mathbf {p}) -\ mathbf {w}\ |=\ izquierda\ |\ izquierda (\ frac {3} {2},\ frac {3} {2}, 4\ derecha)\ derecha\ |=\ sqrt {\ frac {82} {4}} =\ sqrt {20.5}.
\ end {ecuación}\ nonumber\]

Definición\(\PageIndex{2}\)

Supongamos\(L\) y\(M\) son líneas adentro\(\mathbb{R}^n\) con ecuaciones\ (\ begin {ecuación}
\ mathbf {y} =t\ mathbf {v} +\ mathbf {p}
\ end {ecuación}\) y\ (\ begin {ecuación}
\ mathbf {y} =t\ mathbf {w} +\ mathbf {q}
\ end {ecuación}\), respectivamente. Decimos\(L\) y\(M\) somos paralelos si\(\mathbf{v}\) y\(\mathbf{w}\) son paralelos. Decimos\(L\) y\(M\) son perpendiculares, u ortogonales, si se cruzan y\(\mathbf{v}\) y\(\mathbf{w}\) son ortogonales.

Obsérvese que, por definición, una línea es paralela a sí misma.

Figura\(\PageIndex{}\):\ PageIndex {5}\): Líneas paralelas (\(L\)y\(M\)) y perpendiculares (\(L\)y\(N\))

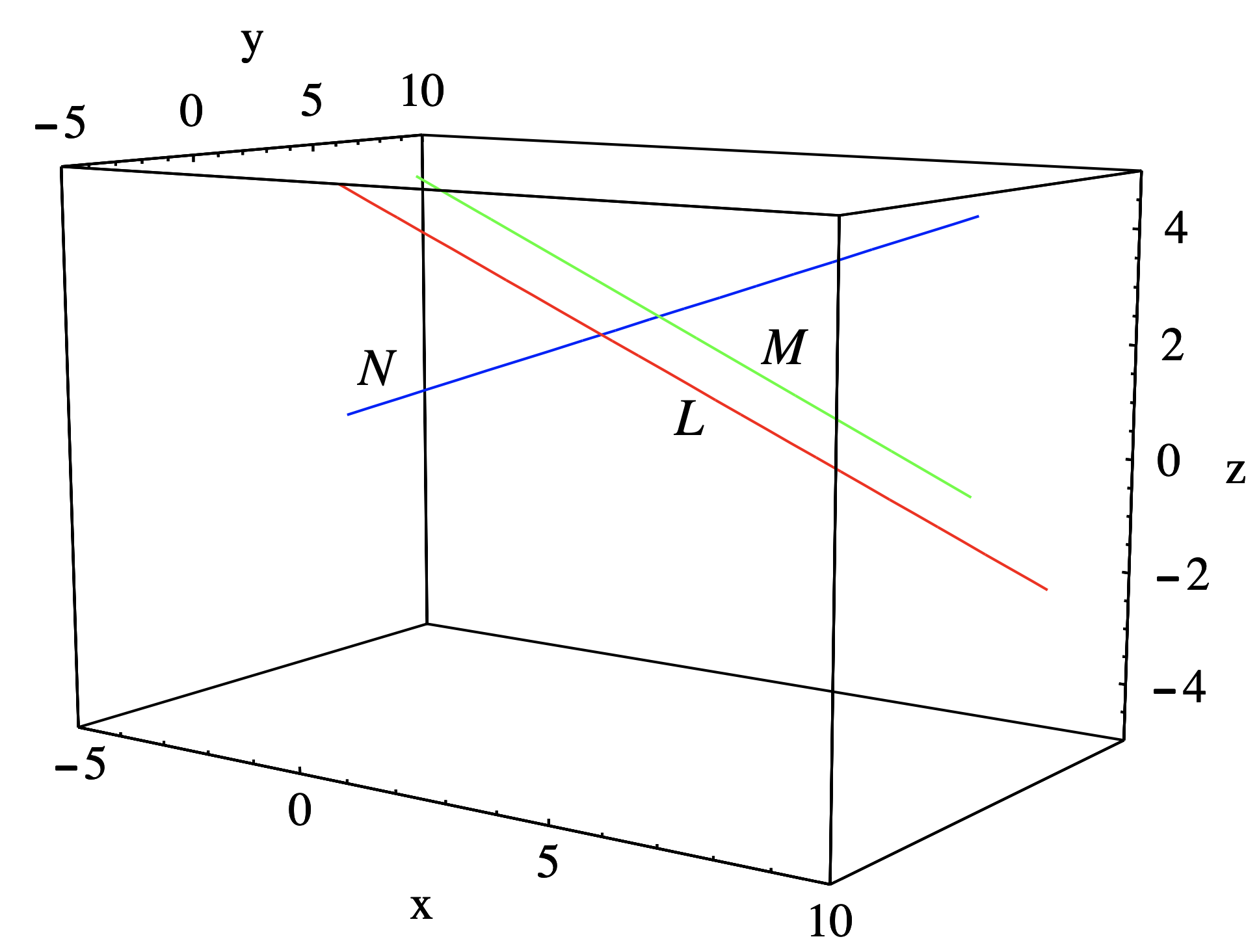
Ejemplo\(\PageIndex{4}\)

Las líneas\(L\) y\(M\) adentro\(\mathbb{R}^3\) con ecuaciones

\ [\ begin {ecuación}
\ mathbf {y} =t (1,2, -1) + (4,1,2)
\ final {ecuación}\ nonumber\]

y

\[\mathbf{y}=t(-2,-4,2)+(5,6,1) , \nonumber \]

respectivamente, son paralelos ya que (−2, −4, 2) = −2 (1, 2, −1), es decir, los vectores (1, 2, −1) y (−2, −4, 2) son paralelos. Ver Figura 1.4.5.

Ejemplo\(\PageIndex{5}\)

Las líneas\(L\) y\(N\) en\(\mathbb{R}^3\) con ecuaciones

\[\mathbf{y}=t(1,2,-1)+(4,1,2) \nonumber \]

y

\[\mathbf{y}=t(3,-1,1)+(-1,5,-1) , \nonumber \]

respectivamente, son perpendiculares ya que se cruzan en (5, 3, 1) (cuando\(t=1\) para la primera línea y\(t=2\) para la segunda línea) y (1, 2, −1) y (3, -1, 1) son ortogonales ya que

\[(1,2,-1) \cdot(3,-1,1)=3-2-1=0 . \nonumber \]

Ver Figura 1.4.5.

Aviones en\(\mathbb{R}^n\)

La siguiente definición es el primer paso para definir un plano.

Definición\(\PageIndex{3}\)

Se dice que dos vectores\(\mathbf{x}\) y\(\mathbf{y}\) in\(\mathbb{R}^n\) son linealmente independientes si ninguno es un múltiplo escalar del otro.

Geométricamente,\(\mathbf{x}\) y\(\mathbf{y}\) son linealmente independientes si no se encuentran en la misma línea a través del origen. Observe que para cualquier vector\(\mathbf{x}\),\(\mathbf{0}\) y no\(\mathbf{x}\) son linealmente independientes, es decir, son linealmente dependientes, ya que\(\mathbf{0}=0 \mathbf{x}\).

Definición\(\PageIndex{4}\)

Dado un vector\(\mathbf{p}\) junto con vectores linealmente independientes\(\mathbf{v}\) y\(\mathbf{w}\), todo ello dentro\(\mathbb{R}^n\), el conjunto de todos los puntos de\(\mathbf{y}\) tal manera que

\[\mathbf{y}=t \mathbf{v}+s \mathbf{w}+\mathbf{p}, \label{1.4.4}\]

donde\(-\infty<t<\infty\) y\(-\infty<s<\infty\), se llama avión.

La intuición aquí es que un plano debe ser un objeto bidimensional, lo cual está garantizado por el requisito de que\(\mathbf{v}\) y\(\mathbf{w}\) sean linealmente independientes. También tenga en cuenta que si dejamos\(\mathbf{y}=\left(y_{1}, y_{2}, \ldots, y_{n}\right)\)\(\mathbf{v}=\left(v_{1}, v_{2}, \ldots, v_{n}\right)\),,\(\mathbf{w}=\left(w_{1}, w_{2}, \ldots, w_{n}\right)\), y\(\mathbf{p}=\left(p_{1}, p_{2}, \ldots, p_{n}\right)\), entonces (\(\ref{1.4.4}\)) implica que

\ [\ begin {align}
y_ {1} =t v_ {1} +s w_ {1} +p_ {1},\ nonumber\\
y_ {2} =t v_ {2} +s w_ {2} +p_ {2},\ nonumber\
\ vdots\ quad\ vdots\ etiqueta {1.4.5}\\
y_ {n} =t v_ {n} +s w_ {n} +p_ {n}. \ nonumber
\ end {align}\]

Al igual que con las líneas, (\(\ref{1.4.4}\)) es una ecuación vectorial para el plano y las ecuaciones en (\(\ref{1.4.5}\)) son ecuaciones paramétricas para el plano.

Ejemplo\(\PageIndex{6}\)

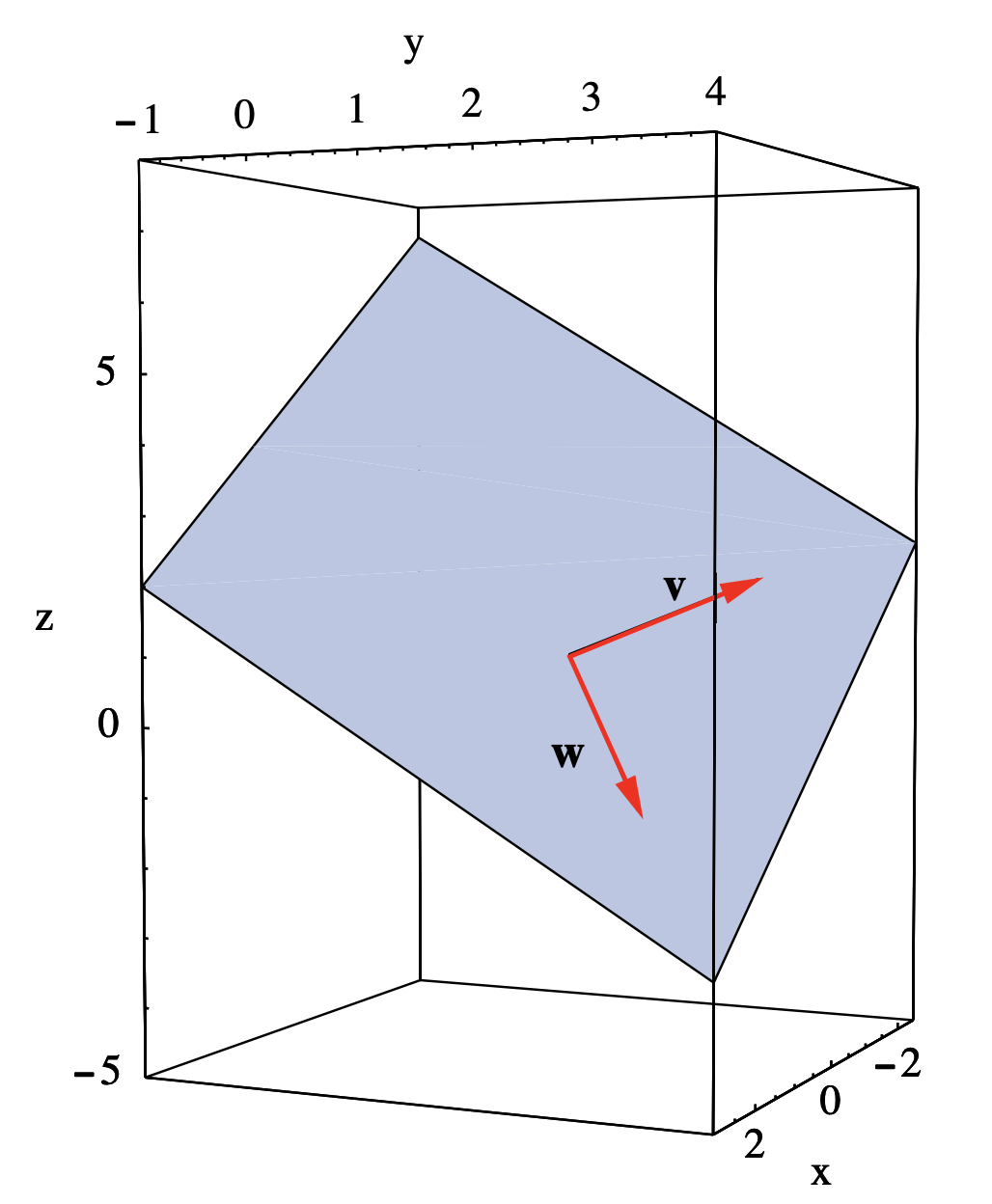
Supongamos que deseamos encontrar una ecuación para el plano P en el\(\mathbb{R}^3\) que contiene los tres puntos\(\mathbf{p}=(1,2,1)\),\(\mathbf{q}=(-1,3,2)\), y\(\mathbf{r}=(2,3,-1)\). El primer paso es encontrar dos vectores linealmente independientes\(\mathbf{v}\) y\(\mathbf{w}\) que se encuentran en el plano. Dado que\(P\) deben contener los segmentos de línea de\(\mathbf{p}\) a\(\mathbf{q}\) y de\(\mathbf{p}\) a\(\mathbf{r}\), podemos tomar\[\mathbf{v}=\mathbf{q}-\mathbf{p}=(-2,1,1)\nonumber \]

y

\[\mathbf{w}=\mathbf{r}-\mathbf{p}=(1,1,-2) . \nonumber \]

Tenga en cuenta que\(\mathbf{v}\) y\(\mathbf{w}\) son linealmente independientes, consecuencia de\(\mathbf{p}\)\(\mathbf{q}\), y\(\mathbf{r}\) no todos tumbados en la misma línea. Ver Figura 1.4.6. Ahora podemos escribir una ecuación vectorial para\(P\) como

\[\mathbf{y}=t(-2,1,1)+s(1,1,-2)+(1,2,1) . \nonumber \]

Tenga en cuenta que\(\mathbf{y}=\mathbf{p}\) cuándo\(t=0\) y\(s=0\),\(\mathbf{y}=\mathbf{q}\) cuándo\(t=1\) y\(s=0\), y\(\mathbf{y}=\mathbf{r}\) cuándo\(t=0\) y\(s=1\). Si escribimos\(\mathbf{y}=(x, y, z)\), entonces, expandiendo la ecuación vectorial,

\[(x, y, z)=t(-2,1,1)+s(1,1,-2)+(1,2,1)=(-2 t+s+1, t+s+2, t-2 s+1) , \nonumber \]

dándonos\ [\ begin {aligned}
&x=-2 t+s+1,\\
&y=t+s+2,\\
&z=t-2 s+1
\ end {alineado}\]

para ecuaciones paramétricas para\(P\).

Figura\(\PageIndex{}\):\ PageIndex {6}\): El plano\(\mathbf{y}=t \mathbf{v}+s \mathbf{w}+\mathbf{p}\), con\(\mathbf{v}=(-2,1,1), \mathbf{w}=(1,1,-2), \mathbf{p}=(1,2,1)\)

Para encontrar la distancia más corta de un punto\(\mathbf{q}\) a un plano\(P\), primero debemos considerar el problema de encontrar la proyección de un vector sobre un plano. Para comenzar, considere el plano\(P\) a través del origen con la ecuación\(\mathbf{y}=t \mathbf{a}+s \mathbf{b}\) donde\(\|a\|=1\),\(\|b\|=1\), y\(\mathbf{a} \perp \mathbf{b}\). Dado un vector\(\mathbf{q}\) que no entra\(P\), vamos

\[\mathbf{r}=(\mathbf{q} \cdot \mathbf{a}) \mathbf{a}+(\mathbf{q} \cdot \mathbf{b}) \mathbf{b} , \nonumber \]

la suma de las proyecciones de\(\mathbf{q}\) sobre\(\mathbf{a}\) y sobre\(\mathbf{b}\). Entonces

\ [\ begin {alineado}
(\ mathbf {q} -\ mathbf {r})\ cdot\ mathbf {a} &=\ mathbf {q}\ cdot\ mathbf {a} -\ mathbf {r}\ cdot\ mathbf {a}\\
&=\ mathbf {q}\ cdot\ mathbf {a} - (\ mathbf {q}\ cdot\ mathbf {a}) (\ mathbf {a}\ cdot\ mathbf {a}) - (\ mathbf {q}\ cdot\ mathbf {b}) (\ mathbf {b}\ cdot\ mathbf {a})\\
&=\ mathbf {q}\ cdot\ mathbf {a} -\ mathbf {q}\ cdot\ mathbf {a} =0,
\ end {alineado}\]

desde\(\mathbf{a} \cdot \mathbf{a}=\|a\|^{2}=1\) y\(\mathbf{b} \cdot \mathbf{a}=0\), y, de manera similar,

\ [\ begin {alineado}
(\ mathbf {q} -\ mathbf {r})\ cdot\ mathbf {b} &=\ mathbf {q}\ cdot\ mathbf {b} -\ mathbf {r}\ cdot\ mathbf {b}\\
&=\ mathbf {q}\ cdot\ mathbf {b} - (\ mathbf {q}\ cdot\ mathbf {a}) (\ mathbf {a}\ cdot\ mathbf {b}) - (\ mathbf {q}\ cdot\ mathbf {b}) (\ mathbf {b}\ cdot\ mathbf {b})\\
&=\ mathbf {q}\ cdot\ mathbf {b} -\ mathbf {q}\ cdot\ mathbf {b} =0.
\ end {alineado}\]

De ello se deduce que para cualquiera\(\mathbf{y}=t \mathbf{a}+s \mathbf{b}\) en el plano P,

\[(\mathbf{q}-\mathbf{r}) \cdot \mathbf{y}=(\mathbf{q}-\mathbf{r}) \cdot(t \mathbf{a}+s \mathbf{b})=t(\mathbf{q}-\mathbf{r}) \cdot \mathbf{a}+s(\mathbf{q}-\mathbf{r}) \cdot \mathbf{b}=0 . \nonumber \]

Es decir,\(\mathbf{q}-\mathbf{r}\) es ortogonal a cada vector en el plano\(P\). Por ello, llamamos a\(\mathbf{r}\) la proyección de\(\mathbf{q}\) sobre el plano\(P\), y observamos que la distancia más corta de\(\mathbf{q}\) a\(P\) es\(\|\mathbf{q}-\mathbf{r}\|\).

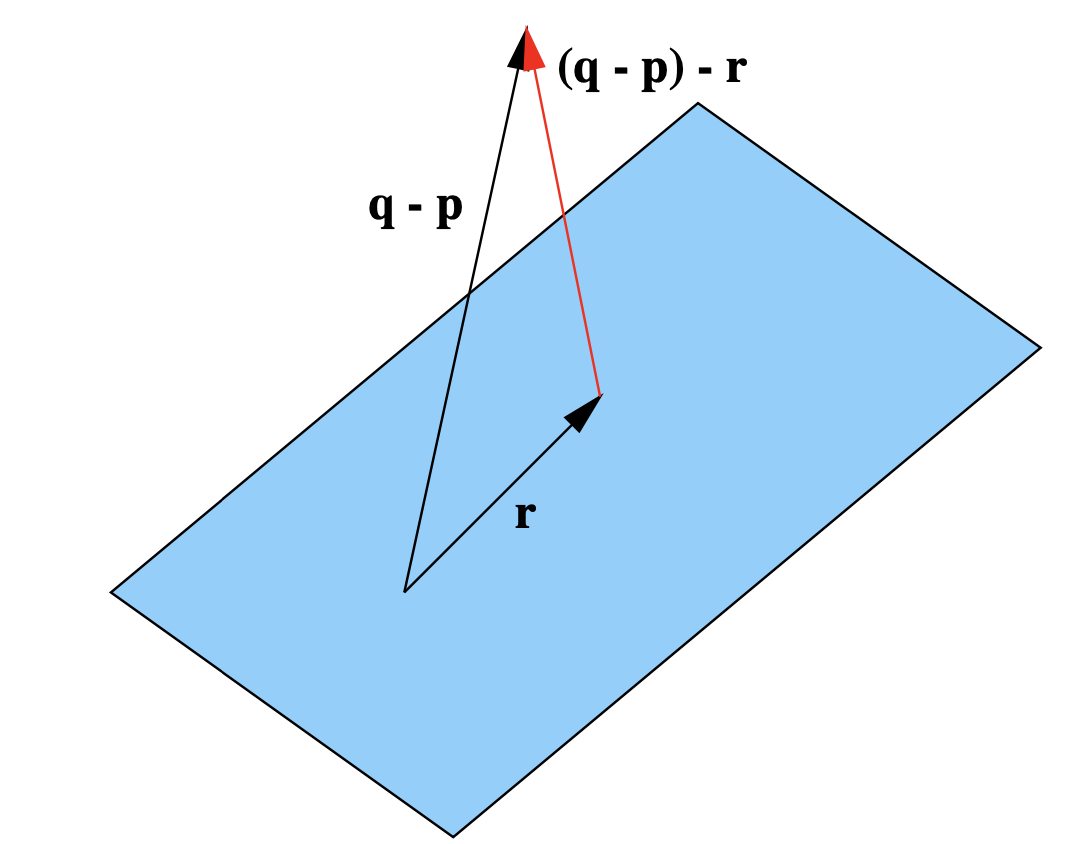
En el caso general, dado un punto\(\mathbf{q}\) y un plano\(P\) con ecuación\(\mathbf{y}=t \mathbf{v}+s \mathbf{w}+\mathbf{p}\), solo necesitamos encontrar vectores\(\mathbf{a}\) y\(\mathbf{b}\) tal que\(\mathbf{a} \perp \mathbf{b}\),\(\|a\|=1\)\(\|b\|=1\), y la ecuación\(\mathbf{y}=t \mathbf{a}+s \mathbf{b}+\mathbf{p}\) describa el mismo plano\(P\). Se le pide en el Ejercicio 29 verificar que si dejamos\(\mathbf{c}\) ser la proyección de\(\mathbf{w}\) sobre\(\mathbf{v}\), entonces podemos tomar

\[\mathbf{a}=\frac{1}{\|\mathbf{v}\|} \mathbf{v} \nonumber \]

y

\[\mathbf{b}=\frac{1}{\|\mathbf{w}-\mathbf{c}\|}(\mathbf{w}-\mathbf{c}) . \nonumber \]

Si\(\mathbf{r}\) es la suma de las proyecciones de\(\mathbf{q}-\mathbf{p}\) onto\(\mathbf{a}\) y\(\mathbf{b}\), entonces r es la proyección de\(\mathbf{q}-\mathbf{p}\) onto\(P\) y\(\|(\mathbf{q}-\mathbf{p})-\mathbf{r}\| \) es la distancia más corta de\(\mathbf{q}\) a\(P\). Ver Figura 1.4.7.

Figura\(\PageIndex{}\):\ PageIndex {7}\): Distancia de un punto\(\mathbf{q}\) a un plano

Ejemplo\(\PageIndex{7}\)

Para calcular la distancia desde el punto\(\mathbf{q}=(2,3,3)\) al plano\(P\) con ecuación

\[\mathbf{y}=t(-2,1,0)+s(1,-1,1)+(-1,2,1) , \nonumber \]

dejar\(\mathbf{v}=(-2,1,0)\),\(\mathbf{w}=(1,-1,1)\), y\(\mathbf{p}=(-1,2,1)\). Luego, usando la notación anterior, tenemos

\ [\ begin {reunió}
\ mathbf {a} =\ frac {1} {\ sqrt {5}} (-2,1,0),\\
\ mathbf {c} =(\ mathbf {w}\ cdot\ mathbf {a})\ mathbf {a} =-\ frac {3} {5} (-2,1,0),
\ end {reunidos}\]

\[ \mathbf{w}-\mathbf{c}=\frac{1}{5}(-1,-2,5) , \nonumber \]

y

\[\mathbf{b}=\frac{1}{\sqrt{30}}(-1,-2,5) . \nonumber \]

Ya que\(\mathbf{q}-\mathbf{p}=(3,1,2)\), la proyección de\(\mathbf{q}-\mathbf{p}\) onto\(P\) es

\[\mathbf{r}=((3,1,2) \cdot \mathbf{a}) \mathbf{a}+((3,1,2) \cdot \mathbf{b}) \mathbf{b}=-(-2,1,0)+\frac{1}{6}(-1,-2,5)=\frac{1}{6}(11,-8,5) \nonumber \]

y

\[(\mathbf{q}-\mathbf{p})-\mathbf{r}=\frac{1}{6}(7,14,7) . \nonumber \]

De ahí que la distancia de\(\mathbf{q}\) a\(P\) sea

\[\|(\mathbf{q}-\mathbf{p})-\mathbf{r}\|=\frac{\sqrt{294}}{6}=\frac{7}{\sqrt{6}} . \nonumber \]

De manera más general, decimos que los vectores\(\mathbf{v}_{1}, \mathbf{v}_{2}, \ldots, \mathbf{v}_{k}\) en\(\mathbb{R}^n\) son linealmente independientes si ninguno de ellos puede escribirse como una suma de múltiplos escalares de los demás. Dado un vector\(\mathbf{p}\) y vectores linealmente independientes\(\mathbf{v}_{1}, \mathbf{v}_{2}, \ldots, \mathbf{v}_{k}\) llamamos al conjunto de todos los puntos de\(\mathbf{y}\) tal manera que

\[ \mathbf{y}=t_{1} \mathbf{v}_{1}+t_{2} \mathbf{v}_{2}+\cdots+t_{k} \mathbf{v}_{k}+\mathbf{p}, \nonumber \]

donde\(-\infty<t_{j}<\infty\),\(j=1,2, \ldots, k\), un subespacio afín k-dimensional de\(\mathbb{R}^n\). En esta terminología, una línea es un subespacio afín unidimensional y un plano es un subespacio afín bidimensional. En lo siguiente, nos interesarán principalmente líneas y planos y así no desarrollaremos los detalles de la situación más general en este momento.

Hiperplanos

Considerar el conjunto\(L\) de todos los puntos\(\mathbf{y}=(x, y)\) en los\(\mathbb{R}^2\) que satisfacer la ecuación

\[ a x+b y+d=0 , \label{1.4.6} \]

donde\(a\),\(b\), y\(d\) son escalares con al menos uno de\(a\) y\(b\) no siendo 0. Si, por ejemplo,\(b \neq 0\), entonces podemos resolver para\(y\), obtener

\[y=-\frac{a}{b} x-\frac{d}{b} . \label{1.4.7} \]

Si establecemos\(x = t\)\(-\infty<t<\infty\), entonces las soluciones a (\(\ref{1.4.6}\)) son

\[\mathbf{y}=(x, y)=\left(t,-\frac{a}{b} t-\frac{d}{b}\right)=t\left(1,-\frac{a}{b}\right)+\left(0,-\frac{d}{b}\right). \label{1.4.8}\]

Así\(L\) es una línea a través\(\left(0,-\frac{d}{b}\right)\) en la dirección de\(\left(1,-\frac{a}{b}\right)\). Un cálculo similar muestra que si\(a \neq 0\), entonces podemos describir\(L\) como la línea a través\( \left(-\frac{d}{a}, 0\right) \) en la dirección de\( \left(-\frac{b}{a}, 1\right) \). De ahí que en cualquier caso\(L\) sea una línea en\( \mathbb{R}^2 \).

Ahora vamos\(\mathbf{n}=(a, b)\) a notar que (\(\ref{1.4.6}\)) es equivalente a

\[ \mathbf{n} \cdot \mathbf{y}+d=0 . \label{1.4.9} \]

Además, si\(\mathbf{p}=\left(p_{1}, p_{2}\right)\) es un punto en\(L\), entonces

\[ \mathbf{n} \cdot \mathbf{p}+d=0, \label{1.4.10} \]

lo que implica eso\(d=-\mathbf{n} \cdot \mathbf{p} \). Así podemos escribir (\(\ref{1.4.9}\)) como

\[ \mathbf{n} \cdot \mathbf{y}-\mathbf{n} \cdot \mathbf{p}=0 \nonumber \]

y así vemos que (\(\ref{1.4.6}\)) es equivalente a la ecuación

\[ \mathbf{n} \cdot(\mathbf{y}-\mathbf{p})=0 . \label{1.4.11} \]

La ecuación (\(\ref{1.4.11}\)) es una ecuación normal para la línea\(L\) y\(\mathbf{n}\) es un vector normal para\(L\). En palabras, (\(\ref{1.4.11}\)) dice que la línea\(L\) consiste en todos los puntos en\( \mathbb{R}^2 \) cuya diferencia con\(\mathbf{p}\) es ortogonal a\(\mathbf{n}\). Ver Figura 1.4.8.

Figura\(\PageIndex{}\):\ PageIndex {8}\):\(L\) es el conjunto de puntos\(\mathbf{y}\) para el cual\(\mathbf{y}-\mathbf{p}\) es ortogonal a\(\mathbf{n}\)

Ejemplo\(\PageIndex{8}\)

Supongamos que\(L\) es una línea\(\mathbb{R}^2\) con ecuación

\[ 2 x+3 y=1 . \nonumber \]

Entonces un vector normal para\(L\) es\(\mathbf{n}=(2,3)\); para encontrar un punto encendido\(L\), observamos que cuando\(x=2\),\(y=-1\), así\(\mathbf{p}=(2,-1)\) es un punto encendido\(L\). Así

\[ (2,3) \cdot((x, y)-(2,-1))=0, \nonumber \]

o, equivalentemente,

\[(2,3) \cdot(x-2, y+1)=0, \nonumber \]

es una ecuación normal para\(L\). Ya que también\(\mathbf{q}=(-1,1)\) es un punto en\(L\),\(L\) tiene dirección\(\mathbf{q}-\mathbf{p}=(-3,2)\). Así

\[ \mathbf{y}=t(-3,2)+(2,-1) \nonumber \]

es una ecuación vectorial para\(L\). Tenga en cuenta que

\[ \mathbf{n} \cdot(\mathbf{q}-\mathbf{p})=(2,3) \cdot(-3,2)=0, \nonumber \]

así\(\mathbf{n}\) es ortogonal a\(\mathbf{q}-\mathbf{p}\).

Ejemplo\(\PageIndex{9}\)

Si\(L\) es una línea\(\mathbb{R}^2\) a través\(\mathbf{p}=(2,3)\) en la dirección de\(\mathbf{v}=(-1,2)\), entonces\(\mathbf{n}=(2,1)\) es un vector normal para\(L\) since\(\mathbf{v} \cdot \mathbf{n}=0 \). Así

\[ (2,1) \cdot(x-2, y-3)=0 \nonumber \]

es una ecuación normal para\(L\). Multiplicando esto, tenemos

\[ 2(x-2)+(y-3)=0 ; \nonumber \]

es decir,\(L\) consta de todos los puntos\((x,y)\) en los\(\mathbb{R}^2\) que satisfacer

\[ 2 x+y=7 \text { . } \nonumber \]

Ahora consideremos el caso donde\(P\) está el conjunto de todos los puntos\(\mathbf{y}=(x, y, z)\) en\(\mathbb{R}^3\) que satisfacen la ecuación

\[ a x+b y+c z+d=0 , \label{1.4.12} \]

donde\(a\),\(b\),\(c\), y\(d\) son escalares con al menos uno de\(a\),\(b\), y\(c\) no siendo 0. Si por ejemplo\(a \neq 0\), entonces podemos resolver\(x\) para obtener

\[ x=-\frac{b}{a} y-\frac{c}{a} z-\frac{d}{a}. \label{1.4.13} \]

Si establecemos\( y=t \)\(-\infty<t<\infty \), y\(z = s\)\(-\infty<s<\infty \), las soluciones a (\(\ref{1.4.12}\)) son

\ [\ begin {align}
\ mathbf {y} &= (x, y, z)\ nonumber\\
&=\ left (-\ frac {b} {a} t-\ frac {c} {a} s-\ frac {d} {a}, t, s\ derecha)\ label {1.4.14}\\
&=t\ left (-\ frac {b} {a}, 1,0\ derecha) +s\ izquierda (-\ frac {c} {a}, 0,1\ derecha) +\ izquierda (-\ frac {d} {a}, 0,0\ derecha). \ nonumber
\ end {align}\]

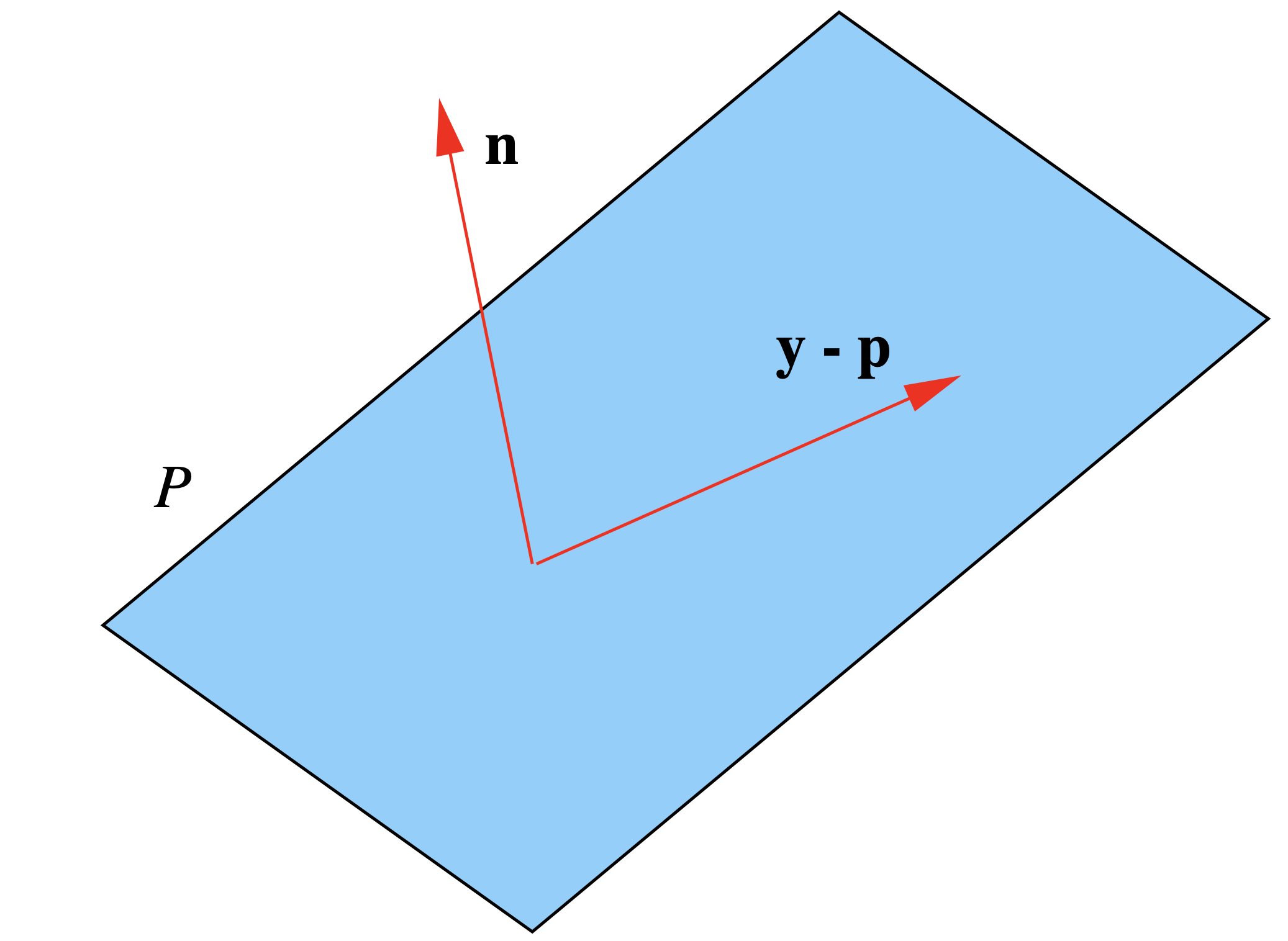
Así vemos que\(P\) es un avión en\(\mathbb{R}^3\). En analogía con el caso de las líneas en\(\mathbb{R}^2\), si dejamos\(\mathbf{n}=(a, b, c)\) y dejamos\(\mathbf{p}=\left(p_{1}, p_{2}, p_{3}\right)\) ser un punto en\(P\), entonces tenemos

\[ \mathbf{n} \cdot \mathbf{p} + d = ax+bby+cz+d=0 , \nonumber \]

de donde vemos eso\( \mathbf{n} \cdot \mathbf{p} = -d\), y así podemos escribir (\(\ref{1.4.12}\)) como

\[ \mathbf{n} \cdot (\mathbf{y} - \mathbf{p} ) =0 . \label{1.4.15} \]

Llamamos a (\(\ref{1.4.15}\)) una ecuación normal para\(P\) y llamamos\(\mathbf{n}\) un vector normal para\(P\). En palabras, (\(\ref{1.4.15}\)) dice que el plano\(P\) consiste en todos los puntos en\(\mathbb{R}^3\) cuya diferencia con\(\mathbf{p}\) es ortogonal a\(\mathbf{n}\). Ver Figura 1.4.9.

Figura\(\PageIndex{}\):\ PageIndex {9}\):\(P\) es el conjunto de puntos\(\mathbf{y}\) para el cual\(\mathbf{y}-\mathbf{p}\) es ortogonal a\(\mathbf{n}\)

Ejemplo\(\PageIndex{10}\)

Dejar\(P\) ser el plano\(\mathbb{R}^3\) con ecuación vectorial

\[ \mathbf{y} = t(2,2,-1) + s(-1,2,1) + (1,1,2) . \nonumber\]

Si lo dejamos\(\mathbf{v}=(2,2,-1)\) y\(\mathbf{w}=(-1,2,1)\), entonces

\[ \mathbf{n} = \mathbf{v} \times \mathbf{w} = (4,-1,6) \nonumber \]

es ortogonal a ambos\(\mathbf{v}\) y\(\mathbf{w}\). Ahora si\(\mathbf{y}\) está encendido\(P\), entonces

\[ \mathbf{y} = t \mathbf{v} + s \mathbf{w} + \mathbf{p} \nonumber \]

para algunos escalares\(t\) y\(s\), de donde vemos que

\[ \mathbf{n} \cdot ( \mathbf{y} - \mathbf{p} ) = \mathbf{n} \cdot (t \mathbf{v} + s \mathbf{w}) = t( \mathbf{n} \cdot \mathbf{v} ) + s ( \mathbf{n} \cdot \mathbf{w} ) = 0+0 = 0 . \nonumber \]

Es decir,\(\mathbf{n}\) es un vector normal para\(P\). Entonces, dejando\(\mathbf{y}=(x, y, z)\),

\[ (4,-1,6) \cdot (x - 1, y-1,z-2) = 0 \label{1.4.16} \]

es una ecuación normal para\(P\). Multiplicando (\(\ref{1.4.16}\)) hacia fuera, vemos que\(P\) consiste en todos los puntos\((x,y,z)\) en los\(\mathbb{R}^3\) que satisfacer

\[ 4x-y+6z=15 . \nonumber \]

Ejemplo\(\PageIndex{11}\)

Supongamos\(\mathbf{p}=(1,2,1)\)\(\mathbf{q}=(-2,-1,3)\),, y\(\mathbf{r}=(2,-3,-1)\) son tres puntos en un plano\(P\) en\(\mathbb{R}^3\). Entonces

\[ \mathbf{v} = \mathbf{q} - \mathbf{p} = (-3,-3,2) \nonumber \]

y

\[\mathbf{w} = \mathbf{r} - \mathbf{p} = (1,-5,-2) \nonumber \]

son vectores sobre los que se encuentran\(P\). Así

\[ \mathbf{n}=\mathbf{v} \times \mathbf{w}=(16,-4,18) \nonumber \]

es un vector normal para\(P\). De ahí

\[ (16,-4,18) \cdot (x-1,y-2,z-1)=0 \nonumber \]

es una ecuación normal para\(P\). Así\(P\) es el conjunto de todos los puntos\((x,y,z)\) en\(\mathbb{R}^3\) satisfacer

\[ 16 x-4 y+18 y=26 . \nonumber \]

La siguiente definición generaliza las ideas en los ejemplos anteriores.

Definición\(\PageIndex{5}\)

Supongamos\(\mathbf{n}\) y\(\mathbf{p}\) son vectores en\(\mathbb{R}^n\) con\(\mathbf{n} \neq \mathbf{0} \). El conjunto de todos los vectores\(\mathbf{y}\) en los\(\mathbb{R}^n\) que satisfacen la ecuación

\[ \mathbf{n} \cdot(\mathbf{y}-\mathbf{p})=0 \label{1.4.17} \]

se llama hiperplano a través del punto\(\mathbf{p}\). Llamamos a\(\mathbf{n}\) un vector normal para el hiperplano y llamamos (\(\ref{1.4.17}\)) una ecuación normal para el hiperplano.

En esta terminología, una línea in\(\mathbb{R}^2\) es un hiperplano y un plano adentro\(\mathbb{R}^3\) es un hiperplano. En general, un hiperplano en\(\mathbb{R}^n\) es un subespacio afín (n − 1) -dimensional de\(\mathbb{R}^n\) . Además, tenga en cuenta que si dejamos\(\mathbf{n}=\left(a_{1}, a_{2}, \ldots, a_{n}\right)\)\(\mathbf{p}=\left(p_{1}, p_{2}, \ldots, p_{n}\right)\),, y\(\mathbf{y}=\left(y_{1}, y_{2}, \ldots, y_{n}\right)\), entonces podemos escribir (\(\ref{1.4.17}\)) como

\[a_{1}\left(y_{1}-p_{1}\right)+a_{2}\left(y_{2}-p_{2}\right)+\cdots+a_{n}\left(y_{n}-p_{n}\right)=0 , \label{1.4.18} \]

o

\[ a_{1} y_{1}+a_{2} y_{2}+\cdots+a_{n} y_{n}+d=0 \label{1.4.19} \]

donde\( d=-\mathbf{n} \cdot \mathbf{p} . \)

Ejemplo\(\PageIndex{12}\)

El conjunto de todos los puntos\((w,x,y,z)\) en los\(\mathbb{R}^4\) que satisfacer

\[ 3 w-x+4 y+2 z=5 \nonumber \]

es un hiperplano tridimensional con vector normal\(\mathbf{n}=(3,-1,4,2)\).

Figura\(\PageIndex{}\):\ PageIndex {10}\): Distancia de un punto\(\mathbf{q}\) a un hiperplano\(H\)

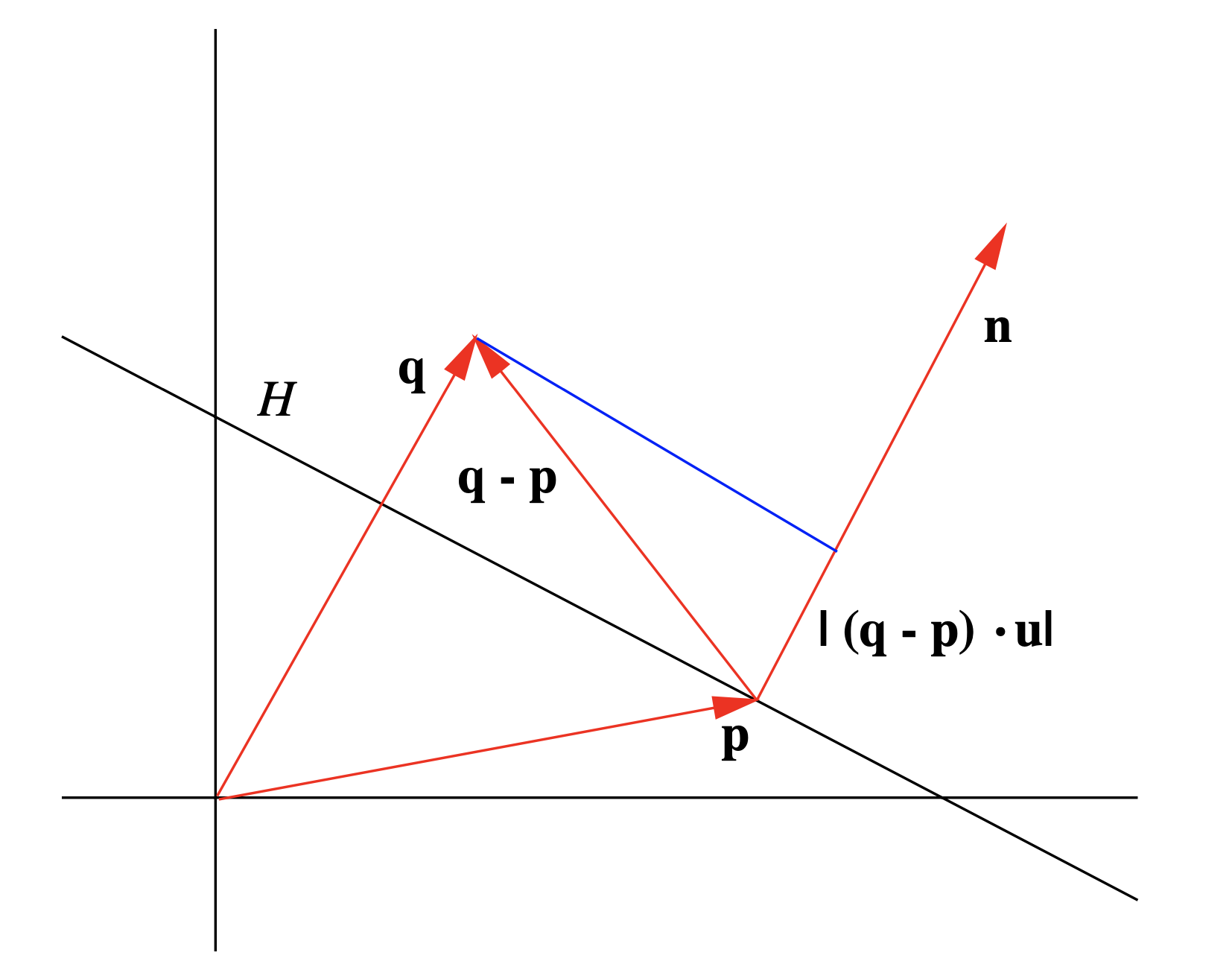
La descripción de la ecuación normal de un hiperplano simplifica una serie de cálculos geométricos. Por ejemplo, dado un hiperplano\(H\) \(\mathbf{p}\)con vector normal\(\mathbf{n}\) y un punto\(\mathbf{q}\) adentro\(\mathbb{R}^n\), la distancia de\(\mathbf{q}\) a\(H\) es simplemente la longitud de la proyección de \(\mathbf{q}-\mathbf{p}\)sobre\(\mathbf{n}\). Así si\(\mathbf{u}\) es la dirección de\(\mathbf{n}\), entonces la distancia de\(\mathbf{q}\) a\(H\) es\(|(\mathbf{q}-\mathbf{p}) \cdot \mathbf{u}| \). Ver Figura 1.4.10. Además, si dejamos\( d=-\mathbf{p} \cdot \mathbf{n} \) como in (\(\ref{1.4.19}\)), entonces tenemos

\[ |(\mathbf{q}-\mathbf{p}) \cdot \mathbf{u}|=|\mathbf{q} \cdot \mathbf{u}-\mathbf{p} \cdot \mathbf{u}|=\frac{\mathbf{q} \cdot \mathbf{n}-\mathbf{p} \cdot \mathbf{n}}{\|\mathbf{n}\|}=\frac{|\mathbf{q} \cdot \mathbf{n}+d|}{\|\mathbf{n}\|} . \label{1.4.20} \]

Tenga en cuenta que, en particular, (\(\ref{1.4.20}\)) se puede utilizar para encontrar la distancia de un punto a una línea en\(\mathbb{R}^2\) y de un punto a un plano en\(\mathbb{R}^3\).

Ejemplo\(\PageIndex{13}\)

Para encontrar la distancia desde el punto\(\mathbf{q}=(2,3,3)\) al plano\(P\) en\(\mathbb{R}^3\) con ecuación

\[ x+2 y+z=4 , \nonumber \]

primero notamos que\(\mathbf{n}=(1,2,1)\) es un vector normal para\(P\). Usando (\(\ref{1.4.20}\)) con\(d = −4\), vemos que la distancia de\(\mathbf{q}\) a\(P\) es

\[ \frac{|\mathbf{q} \cdot \mathbf{n}+d|}{\|\mathbf{n}\|}=\frac{|(2,3,3) \cdot(1,2,1)-4|}{\sqrt{6}}=\frac{7}{\sqrt{6}} . \nonumber \]

Obsérvese que esto concuerda con un ejemplo anterior.

Cerraremos esta sección con unas palabras sobre ángulos entre hiperplanos. Tenga en cuenta que un hiperplano no tiene un vector normal único. En particular, si\(\mathbf{n}\) es un vector normal para un hiperplano\(H\), entonces también\(-\mathbf{n}\) es un vector normal para\(H\). De ahí que siempre es posible elegir los vectores normales requeridos en la siguiente definición.

Definición\(\PageIndex{6}\)

Dejar\(G\) y\(H\) ser hiperplanos\(\mathbb{R}^n\) con ecuaciones normales

\[ \mathbf{m} \cdot(\mathbf{y}-\mathbf{p})=0 \nonumber \]

y

\[ \mathbf{n} \cdot(\mathbf{y}-\mathbf{q})=0 , \nonumber \]

respectivamente, elegidos de tal manera que\(\mathbf{m} \cdot \mathbf{n} \geq 0 \). Entonces el ángulo entre\(G\) y\(H\) es el ángulo entre\(\mathbf{m}\) y\(\mathbf{n}\). Además, diremos eso\(G\) y\(H\) son ortogonales si\(\mathbf{m}\) y\(\mathbf{n}\) son ortogonales y diremos\(G\) y\(H\) son paralelos si\(\mathbf{m}\) y\(\mathbf{n}\) son paralelos.

El efecto de la elección de vectores normales en la definición es hacer que el ángulo entre los dos hiperplanos esté entre 0 y\( \frac{ \pi}{2} \)

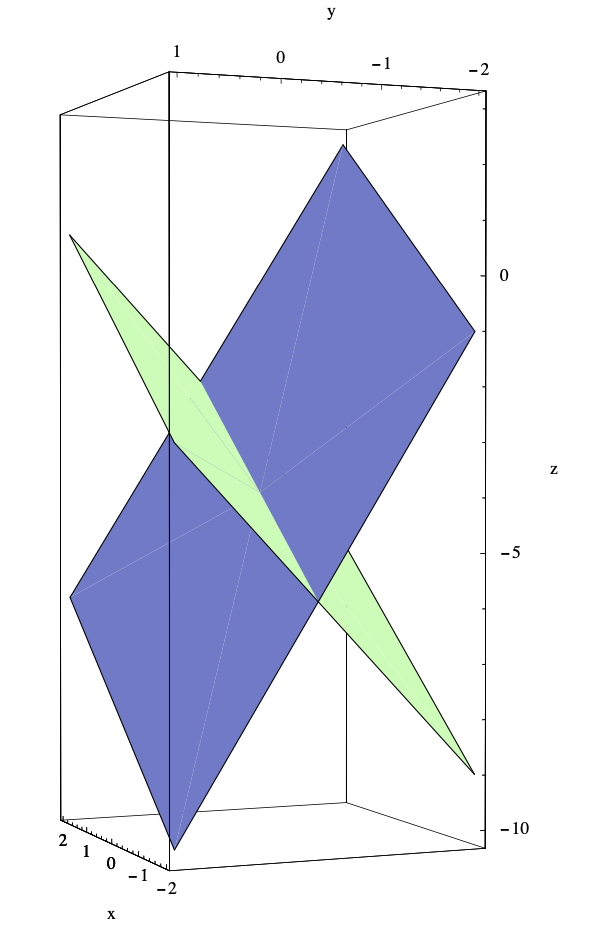
Ejemplo\(\PageIndex{14}\)

Para encontrar el ángulo θ entre los dos planos\(\mathbb{R}^3\) con ecuaciones

\[ x+2 y-z=3 \nonumber \]

y

\[ x-3 y-z=5 , \nonumber \]

primero observamos que los vectores normales correspondientes son\(\mathbf{m}=(1,2,-1)\) y\(\mathbf{n}=(1,-3,-1)\). Ya que\( \mathbf{m} \cdot \mathbf{n}=-4\), calcularemos el ángulo entre\(\mathbf{m}\) y\( - \mathbf{m}\). De ahí

\[ \cos (\theta)=\frac{\mathbf{m} \cdot(-\mathbf{n})}{\|\mathbf{m}\|\|\mathbf{n}\|}=\frac{4}{\sqrt{6} \sqrt{11}}=\frac{4}{\sqrt{66}} . \nonumber \]

Así, redondeando a cuatro decimales,

\[ \theta=\cos ^{-1}\left(\frac{4}{\sqrt{66}}\right)=1.0560. \]

Ver Figura 1.4.11.

Figura\(\PageIndex{}\):\ PageIndex {11}\): Los planos\(x+2 y-z=3\) y\(x-3 y-z=5\)

Ejemplo\(\PageIndex{15}\)

Los planos\(\mathbb{R}^3\) con ecuaciones

\[ 3 x+y-2 z=3 \nonumber \]

y

\[ 6 x+2 y-4 z=13 \nonumber \]

son paralelos ya que sus vectores normales son\(\mathbf{m}=(3,1,-2)\) y\(\mathbf{n}=(6,2,-4)\) y\(\mathbf{n}=2 \mathbf{m} \).