1.6: Operaciones con Matrices

En la sección anterior vimos la importante conexión entre funciones lineales y matrices. En esta sección discutiremos diversas operaciones sobre matrices que encontraremos útiles en nuestro trabajo posterior con funciones lineales.

El álgebra de las matrices

Si\(M\) es una\(n \times m\) matriz con\(a_{i j}\) en la fila\(i\) th y\(j\) th columna,\(i=1,2, \ldots, n, j= 1,2, \ldots, m\), entonces vamos a escribir\(M=\left[a_{i j}\right]\). Con esta notación, las definiciones de suma, resta y multiplicación escalar para matrices son sencillas.

Definición\(\PageIndex{1}\)

Supongamos\(M=\left[a_{i j}\right]\) y\(N=\left[b_{i j}\right]\) son\(n \times m\) matrices y\(c\) es un número real. Luego definimos

\[ M+N=\left[a_{i j}+b_{i j}\right],\]

\[M-N=\left[a_{i j}-b_{i j}\right],\]

y

\[c M=\left[c a_{i j}\right] .\]

En otras palabras, definimos suma, resta y multiplicación escalar para matrices realizando estas operaciones en los elementos individuales de las matrices, de manera similar a la forma en que realizamos estas operaciones en vectores.

Ejemplo\(\PageIndex{1}\)

Si

\ [M=\ left [\ begin {array} {rrr}
1 & 2 & 3\\
-5 & 3 & -1
\ end {array}\ derecha]\ nonumber\]

y

\ [N=\ left [\ begin {array} {rrr}
3 & 1 & 4\\
1 & -3 & 2
\ end {array}\ derecha],\ nonumber\]

entonces, por ejemplo,

\ [\ begin {aligned}
&M+N=\ left [\ begin {array} {rrr}
1+3 & 2+1 & 3+4\\
-5+1 & 3-3 & -1+2
\ end {array}\ right] =\ left [\ begin {array} {rrr}
4 & 3 & 7\\
-4 & 0 & 1
\ end {array}\ right], \\
&M-N=\ left [\ begin {array} {rrr}
1-3 & 2-1 & 3-4\\
-5-1 & 3+3 & -1-2
\ end {array}\ right] =\ left [\ begin {array} {lll}
-2 & 1 & -1\
-6 & 6 & -3
\ end {array}\ right],
\ end {alineado}\ nonumber\]

y

\ [3 M=\ left [\ begin {array} {rrr}
3 & 6 & 9\\
-15 & 9 & -2
\ end {array}\ right]. \ nonumber\]

Estas operaciones tienen interpretaciones naturales en términos de funciones lineales. Supongamos\(L: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\) y\(K: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\) son lineales con\(L(\mathbf{x})=M \mathbf{x}\) y\(K(\mathbf{x})=N \mathbf{x}\) para\(n \times m\) matrices\(M\) y\(N\). Si definimos\(L+K: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}\) por

\[ (L+K)(\mathbf{x})=L(\mathbf{x})+K(\mathbf{x}) ,\]

entonces

\[ (L+K)\left(\mathbf{e}_{j}\right)=L\left(\mathbf{e}_{j}\right)+K\left(\mathbf{e}_{j}\right) \]

para\(j=1,2, \ldots, m\). De ahí que la columna\(j\) th de la matriz que representa\(L+K\) es la suma de las\(j\) th columnas de\(M\) y\(N\). En otras palabras,

\[ (L+K)(\mathbf{x})=(M+N) \mathbf{x}\]

para todos\(\mathbf{x}\) en\(\mathbb{R}^{m}\). Del mismo modo, si definimos\(L-K: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\) por

\[ (L-K)(\mathbf{x})=L(\mathbf{x})-K(\mathbf{x}) ,\]

entonces

\[(L-K)(\mathbf{x})=(M-N) \mathbf{x} .\]

Si, para cualquier escalar\(c\), definimos\(c L: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\) por

\[ c L(\mathbf{x})=c(L(\mathbf{x})) ,\]

entonces

\[ c L\left(\mathbf{e}_{j}\right)=c\left(L\left(\mathbf{e}_{j}\right)\right) \]

para\(j=1,2, \ldots, m\). De ahí que la columna\(j\) th de la matriz que representa\(cL\) es el escalar\(c\) por la\(j\) ésima columna de\(M\). Es decir,

\[ c L(\mathbf{x})=(c M) \mathbf{x} \]

para todos\(\mathbf{x}\) en\(\mathbb{R}^{m}\). En resumen, las operaciones de suma, resta y multiplicación escalar para matrices corresponden de manera natural con las operaciones de suma, resta y multiplicación escalar para funciones lineales.

Consideremos ahora el caso donde\(L: \mathbb{R}^{m} \rightarrow \mathbb{R}^{p}\) y\(K: \mathbb{R}^{p} \rightarrow \mathbb{R}^{n}\) son funciones lineales. Que\(M\) sea la\(p \times m\) matriz tal que\(L(\mathbf{x})=M \mathbf{x}\) para todos\(\mathbf{x}\) entre\(\mathbb{R}^{m}\) y deje\(N\) ser la\(n \times p\) matriz tal que\(K(\mathbf{x})=N \mathbf{x}\) para todos\(\mathbf{x}\) en\(\mathbb{R}^{p}\). Ya que para cualquiera\(\mathbf{x}\) en\(\mathbb{R}^{m}\),\(L(\mathbf{x})\) está en\(\mathbb{R}^{p}\), podemos formar\(K \circ L: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\), la composición de\(K\) con\(L\), definida por

\[ K \circ L(\mathbf{x})=K(L(\mathbf{x})). \]

Ahora

\[ K(L(\mathbf{x}))=N(M \mathbf{x}) ,\]

así que sería natural definir\(NM\), el producto de las matrices\(N\) y\(M\), ser la matriz de\(K \circ L\), en cuyo caso tendríamos

\[ N(M \mathbf{x})=(N M) \mathbf{x}.\]

Así queremos que la columna\(j\) th de\(NM\)\(j=1,2, \ldots, m\),, sea

\[K \circ L\left(\mathbf{e}_{j}\right)=N\left(L\left(\mathbf{e}_{j}\right)\right),\]

que es solo el producto punto de\(L\left(\mathbf{e}_{j}\right)\) con las filas de\(N\). Pero\(L\left(\mathbf{e}_{j}\right)\) es la\(j\) th columna de\(M\), entonces la\(j\) th columna de\(NM\) se forma tomando el producto de punto de la\(j\) th columna de\(M\) con las filas de\(N\). En otras palabras, la entrada en la fila\(i\) th y\(j\) th columna de\(NM\) es el producto de punto de la fila\(i\) th de\(N\) con la\(j\) ésima columna de\(M\). Esto lo escribimos explícitamente en la siguiente definición.

Definición\(\PageIndex{2}\)

Si\(N=\left[a_{i j}\right]\) es una\(n \times p\) matriz y\(M=\left[b_{i j}\right]\) es una\(p \times m\) matriz, entonces definimos el producto de\(N\) y\(M\) para ser la\(n \times m\) matriz\(N M=\left[c_{i j}\right]\), donde

\[ c_{i j}=\sum_{k=1}^{p} a_{i k} b_{k j} , \]

\(i=1,2, \ldots, n \text { and } j=1,2, \ldots, m . \)

Tenga en cuenta que\(NM\) es una\(n \times m\) matriz desde\(K \circ L: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\). Además, el producto\(NM\) de dos matrices\(N\) y\(M\) se define sólo cuando el número de columnas de\(N\) es igual al número de filas de\(M\).

Ejemplo\(\PageIndex{2}\)

Si

\ [N=\ left [\ begin {array} {rr}
1 & 2\\
-1 & 3\\
2 & -2
\ end {array}\ right]\ nonumber\]

y

\ [M=\ left [\ begin {array} {rrrr}
2 & -2 & 1 & 3\\
1 & 2 & -1 & -2
\ end {array}\ right],\ nonumber\]

entonces

\ begin {aligned}
N M &=\ left [\ begin {array} {rr}
1 & 2\\
-1 & 3\\
2 & -2
\ end {array}\ right]\ left [\ begin {array} {rrrr}
2 & -2 & 1 & 3\\
1 & 2 & 2 & 2 & -1 & -2
\ end {array}\ derecha]\\
&=\ left [\ begin {array} {rrrr}
2+2 & -2+4 & 1-2 & 3-4\\
-2+3 & 2+6 & -1-3 & -3-6\\
4-2 & -4-4 & 2+2 & 6+4
\ end {array}\ right]\\
&=\ left [\ begin {array} {rrrr}
4 & 2 & -1 & -1\\
1 & 8 & -4 & -9\\
2 & -8 & 4 & 10
\ end {array}\ right].
\ end {alineado}

Tenga en cuenta que\(N\) \(M\)es\(3 \times 2\)\(2 \times 4\), es y\(NM\) es\(3 \times 4\). Además, tenga en cuenta que no es posible formar el producto en el otro orden.

Ejemplo\(\PageIndex{3}\)

Dejar\(L: \mathbb{R}^{2} \rightarrow \mathbb{R}^{3}\) ser la función lineal definida por

\[ L(x, y)=(3 x-2 y, x+y, 4 y) \nonumber \]

y dejar que\(K: \mathbb{R}^{3} \rightarrow \mathbb{R}^{2}\) sea la función lineal definida por

\[ K(x, y, z)=(2 x-y+z, x-y-z). \nonumber\]

Entonces la matriz para\(L\) es

\ [M=\ left [\ begin {array} {rr}
3 & -2\\
1 & 1\\
0 & 4
\ end {array}\ derecha],\ nonumber\]

la matriz para\(K\) es

\ [N=\ left [\ begin {array} {rrr}
2 & -1 & 1\\
1 & -1 & -1
\ end {array}\ derecha],\ nonumber\]

y la matriz para\(K \circ L: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}\) es

\ [N M=\ left [\ begin {array} {rrr}
2 & -1 & 1\\
1 & -1 & -1
\ end {array}\ right]\ left [\ begin {array} {rr}
3 & -2\\
1 & 1\\
0 & 4
\ end {array}\ right] =\ left [\ begin {array} {ll}
6-1+0 & -4-1+4\\
3-1+0 & -2-1-4
\ end {array}\ right] =\ left [\ begin {array} {ll}
5 & -1\\
2 & -7
\ end {array}\ right]. \ nonumber\]

En otras palabras,

\ [K\ circ L (x, y) =\ left [\ begin {array} {ll}
5 & -1\\
2 & -7
\ end {array}\ right]\ left [\ begin {array} {l}
x\\
y
\ end {array}\ right] =\ left [\ begin {array} {c}
5 x-y\
2 x-7 y
\ end {array}\ derecho]. \ nonumber\]

Tenga en cuenta que en este caso es posible formar la composición en el otro orden. La matriz para\(L \circ K: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3}\) es

\ [M N=\ left [\ begin {array} {rr}
3 & -2\\
1 & 1\\
0 & 4
\ end {array}\ right]\ left [\ begin {array} {rrr}
2 & -1 & 1\\
1 & -1 & -1
\ end {array}\ right] =\ left [\ begin {array} {rrr}
6-2 & -3+2 & 3+2\\
2+1 & -1-1 & 1-1\\
0+4 & 0-4 & 0-4 & 0-4
\ end {array}\ right] =\ left [\ begin {array} {rrr}
4 & -1 & 5\\
3 & -2 & 0\\
4 & -4 & -4
\ end {array }\ derecho],\ nonúmero\]

y así

\ [L\ circ K (x, y, z) =\ left [\ begin {array} {rrr}
4 & -1 & 5\\
3 & -2 & 0\\
4 & -4 & -4
\ end {array}\ right]\ left [\ begin {array} {l}
x\\
y\
z\ end {array}
\ right] =\ left [\ left [\ begin {array} {c}
4 x-y+5 z\\
3 x-2 y\\
4 x-4 y-4 z
\ end {array}\ right]. \ nonumber\]

En particular, tenga en cuenta que no sólo es\(N M \neq M N\), sino que de hecho\(NM\) y ni siquiera\(MN\) son del mismo tamaño.

Determinantes

La noción del determinante de una matriz está estrechamente relacionada con la idea de área y volumen. Para comenzar nuestra definición, considere la\(2 \times 2\) matriz

\ [M=\ left [\ begin {array} {ll}
a_ {1} & a_ {2}\\
b_ {1} & b_ {2}
\ end {array}\ derecha]\ nonumber\]

Figura\(\PageIndex{1}\): Un paralelogramo\(\mathbb{R}^{2}\) con lados adyacentes\(\mathbf{a}\) y\(\mathbf{b}\)

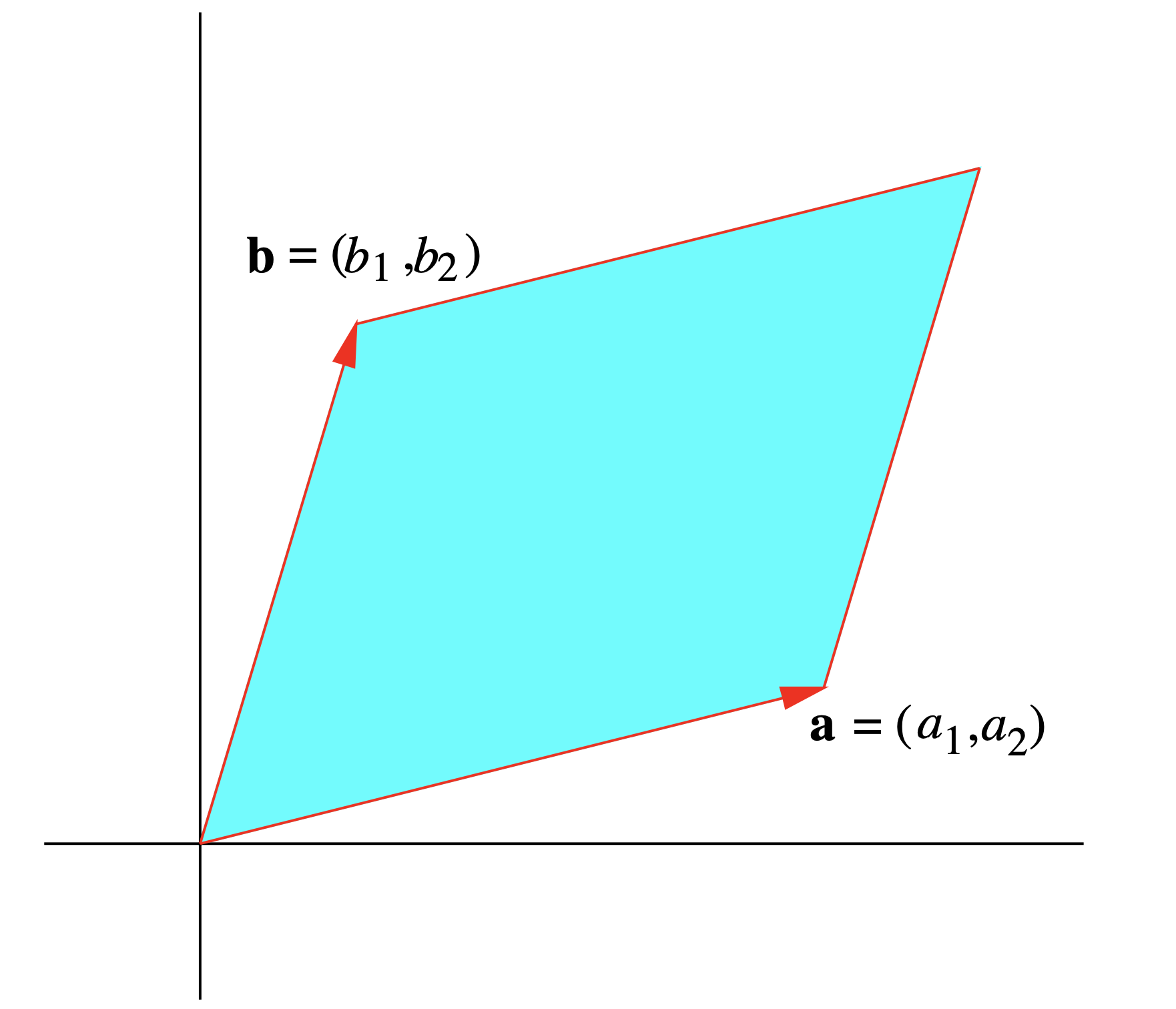
y dejar\(\mathbf{a}=\left(a_{1}, a_{2}\right)\) y\(\mathbf{b}=\left(b_{1}, b_{2}\right)\). Si\(P\) es el paralelogramo que tiene\(\mathbf{a}\) y\(\mathbf{b}\) para lados adyacentes y\(A\) es el área de\(P\) (ver Figura 1.6.1), entonces vimos en la Sección 1.3 que

\[ A=\left\|\left(a_{1}, a_{2}, 0\right) \times\left(b_{1}, b_{2}, 0\right)\right\|=\|\left(0,0, a_{1} b_{2}-a_{2} b_{1} \|=\left|a_{1} b_{2}-a_{2} b_{1}\right|\right. . \]

Esto motiva la siguiente definición.

Definición\(\PageIndex{3}\)

Dada una\(2 \times 2\) matriz

\ [M=\ left [\ begin {array} {ll}
a_ {1} & a_ {2}\\
b_ {1} & b_ {2}
\ end {array}\ derecha],\ nonumber\]

el determinante de\(M\), denotado det (\(M\)), es

\[ \operatorname{det}(M)=a_{1} b_{2}-a_{2} b_{1} . \label{1.6.18} \]

De ahí que tengamos\(A=|\operatorname{det}(M)|\). En palabras, para una\(2 \times 2\) matriz\(M\), el valor absoluto del determinante de\(M\) es igual al área del paralelogramo que tiene las filas de\(M\) para lados adyacentes.

Ejemplo\(\PageIndex{4}\)

Tenemos

\ [\ nombreoperador {det}\ left [\ begin {array} {rr}
1 & 3\\
-4 & 5
\ end {array}\ right] =( 1) (5) - (3) (-4) =5+12=17. \ nonumber\]

Ahora considera una\(3 \times 3\) matriz

\ [M=\ left [\ begin {array} {lll}
a_ {1} & a_ {2} & a_ {3}\\
b_ {1} & b_ {2} & b_ {3}\\
c_ {1} & c_ {2} & c_ {3}
\ end {array}\ derecha]\ nonumber\]

y dejar\(\mathbf{a}=\left(a_{1}, a_{2}, a_{3}\right)\),\(\mathbf{b}=\left(b_{1}, b_{2}, b_{3}\right)\), y\(\mathbf{c}=\left(c_{1}, c_{2}, c_{3}\right)\). Si\(V\) es el volumen del paralelepípedo\(P\) con bordes adyacentes\(\mathbf{a}\),\(\mathbf{b}\), y, luego\(\mathbf{c}\), nuevamente de la Sección 1.3,

\ [\ begin {align}
V &=|\ mathbf {a}\ cdot (\ mathbf {b}\ times\ mathbf {c}) |\ nonumber\\
&=\ izquierda|a_ {1}\ izquierda (b_ {2} c_ {3} -b_ {3} c_ {2}\ derecha) +a_ {2}\ izquierda (b_ {3} -b_ {3} c_ {2}\ izquierda (b_ {3}} c_ {1} -b_ {1} c_ {3}\ derecha) +a_ {3}\ izquierda (b_ {1} c_ {2} -b_ {2} c_ {1}\ derecha)\ derecha|\ nonumber\\
&=\ izquierda|a_ {1}\ operatorname {det}\ left [\ begin {array} {ll}
b_ {2} & b_ {3}\ nonumber\\
c_ {2} & c_ {3}
\ end {array}\ derecha] -a_ {2}\ nombreoperador {det}\ left [\ begin {array} {ll}
b_ {1} & b_ {3}\ nonumber\\
c_ {1} & c_ {3}
\ end {array}\ derecha] +a_ {3}\ nombreoperador {det}\ left [\ begin {array} {ll}
b_ {1} & b_ {2}\ nonumber\\
c_ {1} & c_ {2}
\ end {array}\ derecha]\ derecha|. \ label {}
\ end {align}\]

Definición\(\PageIndex{4}\)

Dada una\(3 \times 3\) matriz

\ [M=\ left [\ begin {array} {lll}
a_ {1} & a_ {2} & a_ {3}\\
b_ {1} & b_ {2} & b_ {3}\\
c_ {1} & c_ {2} & c_ {3}
\ end {array}\ derecha],\ nonumber\]

el determinante de\(M\), denotado det (\(M\)), es

\ [\ nombreoperador {det} (M) =a_ {1}\ nombreoperador {det}\ left [\ begin {array} {ll}
b_ {2} & b_ {3}\
c_ {2} & c_ {3}
\ end {array}\ derecha] -a_ {2}\ nombreoperador {det}\ left [\ begin {array} {ll}
b_ {1} & b_ {3}\\
c_ {1} & c_ {3}
\ fin { array}\ derecha] +a_ {3}\ nombreoperador {det}\ left [\ begin {array} {ll}
b_ {1} & b_ {2}\\
c_ {1} & c_ {2}
\ end {array}\ right]. \ label {1.6.20}\]

Similar al\(2 \times 2\) caso, tenemos\(V=|\operatorname{det}(M)|\).

Ejemplo\(\PageIndex{5}\)

Tenemos

\ begin {aligned}
\ operatorname {det}\ left [\ begin {array} {llr}
2 & 3 & 9\\
2 & 1 & -4\\
5 & 1 & -1
\ end {array}\ right] &=2\ nombreoperador {det}\ left [\ begin {array} {cc}
1 & -4\\
1 & amp; -1
\ end {array}\ right] -3\ operatorname {det}\ left [\ begin {array} {cc}
2 & -4\\
5 & -1
\ end {array}\ right] +9\ nombreoperador {det}\ left [\ begin {array} {cc}
2 & 1\\
5 & 1
\ end {array}\ right]\\
&=2 (-1+4) -3 (-2+20) +9 (2-5)\\
&=6-54-27\\
&=-75.
\ end {alineado}

Dada una\(n \times n \) matriz\(M=\left[a_{i j}\right]\), deja\(M_{i j}\) ser la\((n-1) \times(n-1)\) matriz obtenida eliminando la fila\(i\) th y la\(j\) ésima columna de\(M\). Si para\(n=1\) definimos primero\(\operatorname{det}(M)=a_{11}\) (es decir, el determinante de una\(1 \times 1 \) matriz es solo el valor de su entrada única), entonces podríamos expresar, para\(n=2\), la definición de un el determinante de una\(2 \times 2 \) matriz dada en (\(\ref{1.6.18}\)) en la forma

\[ \operatorname{det}(M)=a_{11} \operatorname{det}\left(M_{11}\right)-a_{12} \operatorname{det}\left(M_{12}\right)=a_{11} a_{22}-a_{12} a_{21}. \]

De igual manera\(n=3\), con, podríamos expresar la definición del determinante de\(M\) dado in (\(\ref{1.6.20}\)) en la forma

\[ \operatorname{det}(M)=a_{11} \operatorname{det}\left(M_{11}\right)-a_{12} \operatorname{det}\left(M_{12}\right)+a_{13} \operatorname{det}\left(M_{13}\right). \]

Siguiendo este patrón, podemos formar una definición recursiva para el determinante de una\(n \times n\) matriz.

Definición\(\PageIndex{5}\)

Supongamos que\(M=\left[a_{i j}\right]\) es una\(n \times n\) matriz y deja\(M_{i j}\) ser la\((n-1) \times(n-1)\) matriz obtenida al eliminar la\(i\) fila y la columna\(j\) th de\(M\),\(i=1,2, \ldots, n\) y\(j=1,2, \ldots, n\). Porque\(n=1\), definimos el determinante de\(M\), denotado\(\operatorname{det}(M)\), por

\[ \operatorname{det}(M)=a_{11} \]

Porque\(n > 1\), definimos el determinante de\(M\), denotado\(\operatorname{det}(M)\), por

\ [\ begin {align}
\ nombreoperador {det} (M) &=a_ {11}\ nombreoperador {det}\ izquierda (M_ {11}\ derecha) -a_ {12}\ nombreoperador {det}\ izquierda (M_ {12}\ derecha) +\ cdots+ (-1) ^ {1+n} a_ {1 n}\ nombreoperador {det}\ izquierda (M_ {1 n}\ derecha)\ nonumber\\
&=\ suma_ {j=1} ^ {n} (-1) ^ {1+j} a_ {1 j}\ nombre_operador {det}\ izquierda (M_ {1 j}\ derecha). \ label {1.6.24}
\ end {align}\]

Llamamos a la definición recursiva porque hemos definido el determinante de una\(n \times n\) matriz en términos de los determinantes de\((n-1) \times(n-1)\) matrices, que a su vez se definen en términos de los determinantes de\((n-2) \times(n-2)\) matrices, y así sucesivamente, hasta que hayamos reducido el problema a computar el determinantes de\(1 \times 1\) matrices.

Ejemplo\(\PageIndex{6}\)

Para un ejemplo del determinante de una\(4 \times 4\) matriz, tenemos

\ begin {aligned}
\ operatorname {det}\ left [\ begin {array} {rrrr}
2 & 1 & 3 & 2\\
2 & 1 & 4 & 1\\
-2 & 3 & -1 & 2\\
1 & 2 & 1 & 1
\ end {array}\ derecha] =2 &\ nombreoperador {det}\ left [\ begin {array} {rrr}
1 & 4 & 1\\
3 & -1 & 2\\
2 & 1 & 1
\ end {array}\ right] -\ nombre del operador {det}\ left [\ begin {array} {rrr}
2 & 4 & 1\
-2 & -1 & 2\\
1 & 11 & amp; 1
\ end {array}\ right]\\
&+3\ operatorname {det}\ left [\ begin {array} {rrr}
2 & 1 & 1\\
-2 & 3 & 2\\
1 & 2 & 2 & 1
\ end {array}\ derecha] -2\ nombreoperador {det}\ left [\ begin {array} {rrr}
2 & 1 & 4\\
-2 & 3 & -1\\
1 & 2 & 1 & 1
\ end {array}\ derecha]\\
=& 2 ((-1-2) -4 (3-4) + (3+2)) - (2 (-1-2)\\
&\ quad-4 (-2-2) + (-2+1)) +3 (2 (3-4) - (-2-2)\\
&+ (-4-3)) -2 (2 (2 (3+2) - (-2+1) +4 (-4-3))\\
=& 2 (-3+4+5) - (-6+16-1) +3 (-2+4-7)\\
&\ quad-2 (10+1-28)\\
=& 12-9-15+34\\
=& 22.
\ end {alineado}

El siguiente teorema establece que no hay nada especial en usar la primera fila de la matriz en la expansión del determinante especificado en (\(\ref{1.6.24}\)), ni hay nada especial en expandirse a lo largo de una fila en lugar de una columna. El efecto práctico es que podemos calcular el determinante de una matriz dada expandiéndose a lo largo de cualquier fila o columna que sea más conveniente. La prueba de este teorema nos llevaría demasiado lejos en este punto, por lo que la omitiremos (pero se le pedirá que verifique el teorema para los casos especiales\(n=2\) y\(n=3\) en el Ejercicio 10).

Teorema\(\PageIndex{1}\)

Dejar\(M=\left[a_{i j}\right]\) ser una\(n \times n\) matriz y dejar\(M_{i j}\) ser la\((n-1) \times(n-1)\) matriz obtenida eliminando la fila\(i\) th y la\(j\) ésima columna de\(M\). Entonces para cualquier\(i=1,2, \ldots, n\),

\[ \operatorname{det}(M)=\sum_{j=1}^{n}(-1)^{i+j} a_{i j} \operatorname{det}\left(M_{i j}\right), \]

y para cualquier\(j=1,2, \ldots, n\),

\[ \operatorname{det}(M)=\sum_{i=1}^{n}(-1)^{i+j} a_{i j} \operatorname{det}\left(M_{i j}\right), \label{1.6.26} \]

Ejemplo\(\PageIndex{7}\)

La forma más sencilla de calcular el determinante de la matriz

\ [M=\ left [\ begin {array} {rrr}
4 & 0 & 3\\
2 & 3 & 1\\
-3 & 0 & -2
\ end {array}\ derecha]\ nonumber\]

es expandirse a lo largo de la segunda columna. A saber,

\ begin {aligned}
\ operatorname {det} (M) =& (-1) ^ {1+2} (0)\ operatorname {det}\ left [\ begin {array} {rr}
2 & 1\\
-3 & -2
\ end {array}\ right] + (-1) ^ {2+2} (3)\ nombreoperador {det}\ left [\ begin {array} {rr}
4 & 3\\
-3 y -2
\ end {array}\ right]\\
&+ (-1) ^ {3+2} (0)\ nombreoperador {det}\ left [\ begin {array} {ll}
4 & 3\\
2 & 1
\ end {array}\ derecha]\\
=& 3 (-8+9)\\
=& 3.
\ end {alineado}

Debe verificar que expandirse a lo largo de la primera fila, como hicimos en la definición del determinante, da el mismo resultado.

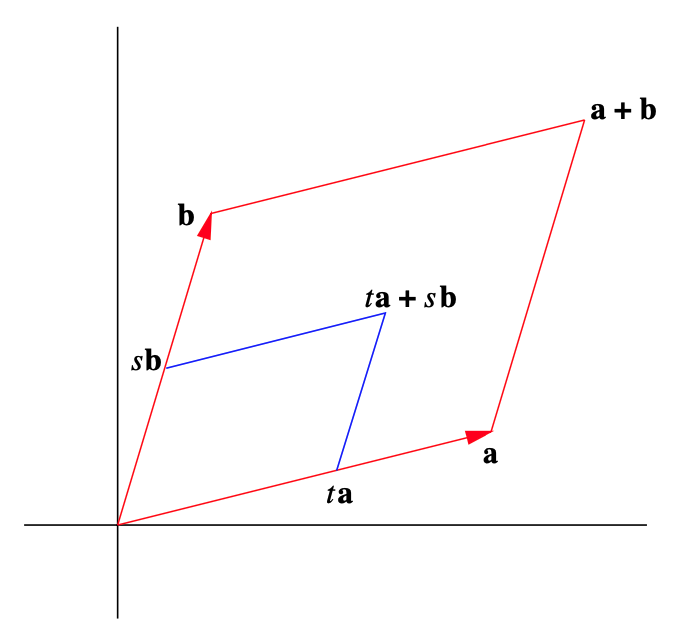
Para volver al problema de la computación de volúmenes, necesitamos definir un paralelepípedo en\(\mathbb{R}^{n}\). Primero tenga en cuenta que si\(P\) es un paralelogramo\(\mathbb{R}^{2}\) con lados adyacentes dados por los vectores\(\mathbf{a}\) y\(\mathbf{b}\), luego

\[ P=\{\mathbf{y}: \mathbf{y}=t \mathbf{a}+s \mathbf{b}, 0 \leq t \leq 1,0 \leq s \leq 1\}. \]

Es decir, para\(0 \leq t \leq 1\),\(\text { ta }\) es un punto entre\(\mathbf{0}\) y\(\mathbf{a}\), y para\(0 \leq s \leq 1\),\(s \mathbf{b}\) es un punto entre\(\mathbf{0}\) y\(\mathbf{b}\); de ahí\(t \mathbf{a}+s \mathbf{b}\) es un punto en el paralelogramo\(P\). Además, cada punto en\(P\) puede expresarse en esta forma. Ver Figura 1.6.2. La siguiente definición generaliza esta caracterización de paralelogramos.

Figura\(\PageIndex{2}\): Un paralelogramo\(\mathbb{R}^{2}\) con lados adyacentes\(\mathbf{a}\) y\(\mathbf{b}\)

Definición\(\PageIndex{6}\)

Dejar\(\mathbf{a}_{1}, \mathbf{a}_{2}, \ldots, \mathbf{a}_{n}\) ser vectores linealmente independientes en\(\mathbb{R}^{n}\). Llamamos

\[ P=\left\{\mathbf{y}: y=t_{1} \mathbf{a}_{1}+t_{2} \mathbf{a}_{2}+\cdots+t_{n} \mathbf{a}_{n}, 0 \leq t_{i} \leq 1, i=1,2, \ldots, n\right\} \]

un paralelepípedo n-dimensional con bordes adyacentes\(\mathbf{a}_{1}, \mathbf{a}_{2}, \ldots, \mathbf{a}_{n}\).

Definición\(\PageIndex{7}\)

Dejar\(P\) ser un paralelepípedo n-dimensional con bordes adyacentes\(\mathbf{a}_{1}, \mathbf{a}_{2}, \ldots, \mathbf{a}_{n}\) y dejar\(M\) ser la\(n \times n\) matriz que tiene\(\mathbf{a}_{1}, \mathbf{a}_{2}, \ldots, \mathbf{a}_{n}\) para sus filas. Entonces el volumen de\(P\) se define para ser\(|\operatorname{det}(M)| \).

Se puede mostrar, usando (\(\ref{1.6.26}\)) e inducción, que si\(N\) es la matriz obtenida intercambiando las filas y columnas de una\(n \times n\) matriz\(M\), entonces\(\operatorname{det}(N)=\operatorname{det}(M)\) (ver Ejercicio 12). Así podríamos haber definido\(M\) en la definición anterior usando\(\mathbf{a}_{1}, \mathbf{a}_{2}, \ldots, \mathbf{a}_{n}\) para columnas en lugar de filas.

Ahora supongamos que\(L: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}\) es lineal y deja\(M\) ser la\(n \times n\) matriz tal que\( L(\mathbf{x})=M \mathbf{x} \) para todos\(\mathbf{x}\) adentro\(\mathbb{R}^{n}\). Dejar\(C\) ser el paralelepípedo\(n\) -dimensional con bordes adyacentes\(\mathbf{e}_{1}, \mathbf{e}_{2}, \ldots, \mathbf{e}_{n}\), los vectores base estándar para\(\mathbb{R}^{n}\). Entonces\(C\) es un\(1 \times 1\) cuadrado cuando\(n=2\) y un\(1 \times 1 \times 1\) cubo cuando\(n=3\). En general, podemos pensar en un cubo unitario\(n\) -dimensional.\(C\) Obsérvese que el volumen de\(C\) es, por definición,

\ [\ nombreoperador {det}\ left [\ begin {array} {ccccc}
1 & 0 & 0 &\ cdots & 0\\ cdots &
0 &\ 0 &\ cdots & 0\\ cdots &
0\\ cdots & 0\\ vdots &
\ vdots &\ vdots &\ vdots &\ ddots &\ vdots &\ vdots\\
0 & amp; 0 & 0 &\ cdots & 1
\ end {array}\ right] =1. \ nonumber\]

Supongamos que\(L\left(\mathbf{e}_{1}\right), L\left(\mathbf{e}_{2}\right), \ldots, L\left(\mathbf{e}_{n}\right)\) son linealmente independientes y dejan\(P\) ser el paralelepípedo\(n\) -dimensional con bordes adyacentes\(L\left(\mathbf{e}_{1}\right), L\left(\mathbf{e}_{2}\right), \ldots, L\left(\mathbf{e}_{n}\right)\). Tenga en cuenta que si

\[ \mathbf{x}=t_{1} \mathbf{e}_{1}+t_{2} \mathbf{e}_{2}+\cdots+t_{n} \mathbf{e}_{n} , \nonumber \]

donde\(0 \leq t_{k} \leq 1\) para\(k=1,2, \ldots, n\), es un punto en\(C\), entonces

\[ L(\mathbf{x})=t_{1} L\left(\mathbf{e}_{1}\right)+t_{2} L\left(\mathbf{e}_{2}\right)+\cdots+t_{n} L\left(\mathbf{e}_{n}\right) \nonumber \]

es un punto en\(P\). De hecho,\(L\) mapea el cubo de la unidad n-dimensional\(C\) exactamente en el\(n\) paralelepípedo dimensional\(P\). Ya que\(L\left(\mathbf{e}_{1}\right), L\left(\mathbf{e}_{2}\right), \ldots, L\left(\mathbf{e}_{n}\right)\) son las columnas de\(M\), se deduce que el volumen de\(P\) iguales\(|\operatorname{det}(M)|\). En otras palabras,\(|\operatorname{det}(M)|\) mide cuánto\(L\) estira o encoge el volumen de un cubo unitario.

Teorema\(\PageIndex{2}\)

Supongamos que\(L: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}\) ^\(M\)es lineal y es la\(n \times n\) matriz tal que\(L(\mathbf{x})=M \mathbf{x}\). Si\(L\left(\mathbf{e}_{1}\right), L\left(\mathbf{e}_{2}\right), \ldots, L\left(\mathbf{e}_{n}\right)\) son lineales independientes y\(P\) es el paralelepípedo\(n\) -dimensional con bordes adyacentes\(L\left(\mathbf{e}_{1}\right), L\left(\mathbf{e}_{2}\right), \ldots, L\left(\mathbf{e}_{n}\right)\), entonces el volumen de\(P\) es igual a\(|\operatorname{det}(M)|\).