2.2.E: Mejores aproximaciones afín (ejercicios)

Ejercicio\(\PageIndex{1}\)

Encuentra la derivada de cada una de las siguientes funciones.

a)\(f(t)=\left(t^{3}, t, 2 t+4\right)\)

b)\(g(t)=(3 t \cos (2 t), 4 t \sin (2 t))\)

c)\(h(t)=\left(4 t^{3}-3, \sin (t), e^{-2 t}\right)\)

d)\(f(t)=\left(e^{-t} \sin (3 t), e^{-t} \cos (3 t), t e^{-t}\right)\)

Responder

a)\(D f(t)=\left(3 t^{2}, 1,2\right)\)

c)\(D h(t)=\left(12 t^{2}, \cos (t),-2 e^{-2 t}\right)\)

Ejercicio\(\PageIndex{2}\)

Para cada una de las siguientes, encuentra la mejor aproximación afín a\(f\) en el punto dado.

a)\(f(t)=\left(t, t^{3}\right), t=2\)

b)\(f(t)=(3 \sin (2 t), 4 \cos (2 t)), t=\frac{\pi}{6}\)

c)\(f(t)=(\cos (t), \sin (t), \cos (2 t)), t=\frac{\pi}{3}\)

d)\(f(t)=(2 \cos (2 t), 3 \sin (2 t), 3 t), t=0\)

Responder

a)\(A(t)=(1,12)(t-2)+(2,8)\)

c)\(A(t)=\left(-\frac{\sqrt{3}}{2}, \frac{1}{2},-\sqrt{3}\right)\left(t-\frac{\pi}{3}\right)+\left(\frac{1}{2}, \frac{\sqrt{3}}{2},-\frac{1}{2}\right)\)

Ejercicio\(\PageIndex{3}\)

Deje que\(f(t)=(2 \cos (\pi t), 3 \sin (\pi t))\) entre parametrizar una elipse\(E\) \(\mathbb{R}^2\). Trazar\(E\) junto con la línea tangente en\(f\left(\frac{2}{3}\right)\).

Ejercicio\(\PageIndex{4}\)

Dejar\(f(t)=((1+2 \cos (t)) \cos (t),(1+2 \cos (t)) \sin (t))\) parametrizar una curva\(C\) en\(\mathbb{R}^2\). Trazar\(C\) junto con la línea tangente en\(f\left(\frac{\pi}{6}\right)\).

Ejercicio\(\PageIndex{5}\)

Dejar\(h(t)=\left(\sin (2 \pi t), \cos (2 \pi t), \frac{t}{2}\right)\) parametrizar una hélice\(H\) circular\(\mathbb{R}^3\). Trazar\(H\) junto con la línea tangente en\(h\left(\frac{3}{2}\right)\).

Ejercicio\(\PageIndex{6}\)

Dejar\(g(t)=(\cos (\pi t), \sqrt{t}, \sin (\pi t))\) parametrizar una curva\(C\) en\(\mathbb{R}^3\). Trazar\(C\) junto con la línea tangente en\(g\left(\frac{1}{4}\right)\).

Ejercicio\(\PageIndex{7}\)

Supongamos que\(f: \mathbb{R} \rightarrow \mathbb{R}^{2}\) se define por\(f(t)=(t, \varphi(t))\), donde\(\varphi: \mathbb{R} \rightarrow \mathbb{R}\) es diferenciable, y dejar que\(C\) sea la curva en\(\mathbb{R}^2\) parametrizada por\(f\). Mostrar que la línea tangente a\(C\) at\(f(c)\) es la misma que la línea tangente a la gráfica de\(\varphi\) at\((c, \varphi(c)\).

Responder

Tenga en cuenta que la línea tangente a\(C\) at\(f(c)\) está parametrizada por

\[ A(t)=\left(1, \varphi^{\prime}(c)\right)(t-c)+(c, \varphi(c))=\left(t, \varphi^{\prime}(c)(t-c)+\varphi(c)\right) \nonumber \]

Ejercicio\(\PageIndex{8}\)

Dejar\(C\) ser la curva en\(\mathbb{R}^2\) parametrizada por\(f(t)=\left(t^{3}, t^{6}\right),-\infty<t<\infty .\) Es\(f\) una parametrización suave de\(C\)? Si no, ¿se puede encontrar una parametrización suave de\(C\)?

Responder

No, no\(f\) es una parametrización suave de\(C\) desde entonces\(D f(0)=(0,0)\). Sin embargo\(g(t)=\left(t, t^{2}\right),-\infty<t<\infty\),, es una parametrización suave de\(C\).

Ejercicio\(\PageIndex{9}\)

Dejar\(C\) ser la curva en\(\mathbb{R}^2\) parametrizada por\(f(t)=\left(t^{2}, t^{2}\right),-\infty<t<\infty\). Demostrar que no\(f\) es una parametrización suave de\(C\). ¿Dónde está el problema? Trazar\(C\) e identificar la ubicación del problema.

Responder

\(f\)no es una parametrización suave de\(C\) desde entonces\(D f(0)=(0,0)\).

Ejercicio\(\PageIndex{10}\)

Dejar\(\mathbf{v} \neq \mathbf{0}\) y\(\mathbf{p}\) ser vectores en\(\mathbb{R}^n\) y dejar\(C\) ser la curva en\(\mathbb{R}^n\) parametrizada por\(f(t)=t \mathbf{v}+\mathbf{p}\). ¿Cuál es la mejor aproximación afín a\(f\) at\(t=t_{0}\)?

Ejercicio\(\PageIndex{11}\)

Para cada una de las siguientes, encuentra el vector tangente unitario y el vector normal de unidad principal en el punto indicado.

a)\(f(t)=\left(t, t^{2}\right), t=1\)

b)\(g(t)=(3 \sin (2 t), 3 \cos (2 t)), t=\frac{\pi}{3}\)

c)\(f(t)=(2 \cos (t), 4 \sin (t)), t=\frac{\pi}{4}\)

d)\(h(t)=(\cos (\pi t), 2 \sin (\pi t)), t=\frac{3}{4}\)

e)\(g(t)=(\cos (t), \sin (t), t), t=\frac{\pi}{3}\)

f)\(f(t)=(2 \sin (t), 3 \cos (2 t), 2 t), t=\frac{\pi}{4}\)

g)\(f(t)=(\sin (\pi t),-\cos (\pi t), 3 t), t=\frac{1}{2}\)

h)\(g(t)=\left(\cos \left(\pi t^{2}\right), \sin \left(\pi t^{2}\right), t^{2}\right), t=1\)

i)\(f(t)=\left(t, t^{2}, t^{3}\right), t=2\)

Responder

a)\(T(1)=\frac{1}{\sqrt{5}}(1,2) ; N(1)=\frac{1}{\sqrt{5}}(-2,1)\)

c)\(T\left(\frac{\pi}{4}\right)=\frac{1}{\sqrt{5}}(-1,2) ; N\left(\frac{\pi}{4}\right)=-\frac{1}{\sqrt{5}}(2,1)\)

e)\(T\left(\frac{\pi}{3}\right)=\left(-\frac{1}{2} \sqrt{\frac{3}{2}}, \frac{1}{2 \sqrt{2}}, \frac{1}{\sqrt{2}}\right) ; N\left(\frac{\pi}{3}\right)=\left(-\frac{1}{2},-\frac{\sqrt{3}}{2}, 0\right)\)

g)\(T\left(\frac{1}{2}\right)=\left(0, \frac{\pi}{\sqrt{9+\pi^{2}}}, \frac{3}{\sqrt{9+\pi^{2}}}\right) ; N\left(\frac{1}{2}\right)=(-1,0,0)\)

i)\(T(2)=\frac{1}{\sqrt{161}}(1,4,12) ; N(2)=\frac{1}{\sqrt{29141}}(-76,-143,54)\)

Ejercicio\(\PageIndex{12}\)

Usa el hecho de que\(f(t)=(b \cos (t), b \sin (t))\) parametriza un círculo de radio\(b\) para mostrar que un radio de un círculo siempre es perpendicular a la línea tangente en el punto donde el radio toca el círculo.

Ejercicio\(\PageIndex{13}\)

Verificar (2.2.21); es decir, mostrar que si\(f: \mathbb{R} \rightarrow \mathbb{R}^{n}\) y\(\varphi: \mathbb{R} \rightarrow \mathbb{R}\) son ambos diferenciables, entonces

\[D(\varphi(t) f(t))=\varphi(t) D f(t)+\varphi^{\prime}(t) f(t). \nonumber \]

Ejercicio\(\PageIndex{14}\)

Supongamos\(f: \mathbb{R} \rightarrow \mathbb{R}^{3}\) y ambos\(g: \mathbb{R} \rightarrow \mathbb{R}^{3}\) son diferenciables. Demostrar que

\[ D(f(t) \times g(t))=f(t) \times D g(t)+D f(t) \times g(t), \nonumber \]

otra versión más de la regla del producto.

Ejercicio\(\PageIndex{15}\)

La siguiente figura ilustra una curva en ^R2 parametrizada por alguna función\(f: \mathbb{R} \rightarrow \mathbb{R}^{2}\). Si\(\mathbf{T}\) es el vector tangente unitario en el punto indicado en la curva, entonces cualquiera\(\mathbf{M}\) o\(\mathbf{N}\) es el vector normal de unidad principal en ese punto. ¿Cuál es?

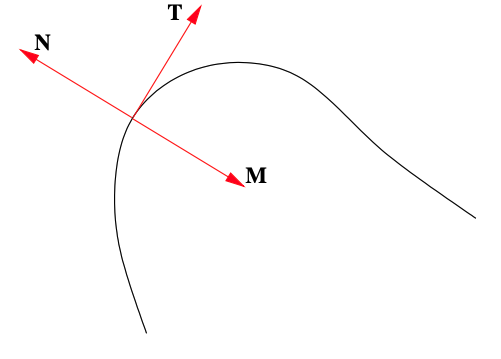
Responder

\(M\)