3.5: Valores extremos

Después de algunos resultados preliminares y definiciones, aplicaremos nuestro trabajo de las secciones anteriores al problema de encontrar valores máximos y mínimos de funciones de valor escalar de varias variables. La historia aquí es paralela en gran medida a la historia del cálculo de una variable, con los inevitables giros y vueltas debido a la presencia de variables adicionales. Comenzaremos con una definición muy similar a la definición análoga para funciones de una sola variable.

El Teorema del Valor Extremo

Definición\(\PageIndex{1}\)

Supongamos que\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) se define en un conjunto\(S\). Decimos que\(f\) tiene un valor máximo de\(M\) al\(\mathbf{c}\) si\(f(\mathbf{c})=M\) y\(M \geq f(\mathbf{x})\) para todos\(\mathbf{x}\) en\(S\). Decimos que\(f\) tiene un valor mínimo de\(m\) al\(\mathbf{c}\) si\(f(\mathbf{c})=m\) y\(m \leq f(\mathbf{x})\) para todos\(\mathbf{x}\) en\(S\).

A los valores máximo y mínimo de la definición anterior se les hace referencia a veces como valores máximos y mínimos globales para distinguirlos de los valores máximos y mínimos locales de la siguiente definición.

Definición\(\PageIndex{2}\)

Supongamos que\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) se define en un conjunto abierto\(U\). Decimos que\(f\) tiene un valor máximo local de\(M\) a\(\mathbf{c}\) si\(f(\mathbf{c})=M\) y\(M \geq f(\mathbf{x})\) para todos\(\mathbf{x}\) en\(B^{n}(\mathbf{c}, r)\) para algunos\(r>0\). Decimos que\(f\) tiene un valor mínimo local de\(m\) a\(\mathbf{c}\) si\(f(\mathbf{c})=m\) y\(m \leq f(\mathbf{x})\) para todos\(\mathbf{x}\) en\(B^{n}(\mathbf{c}, r)\) para algunos\(r>0\).

Digamos valor extremo, o valor extremo global, cuando nos referimos a un valor del\(f\) cual es un valor máximo global o un valor mínimo global, y valor extremo local cuando se refiere a un valor que es un máximo local o un mínimo local valor.

En el cálculo de una variable, el Teorema del Valor Extremo, la afirmación de que cada función continua en un intervalo cerrado finito tiene un valor máximo y un valor mínimo, fue extremadamente útil en la búsqueda de valores extremos. Hay un resultado similar para nuestra situación actual, pero primero necesitamos la siguiente definición.

Definición\(\PageIndex{3}\)

Decimos que un set\(S\) in\(\mathbb{R}^n\) está acotado si existe un\(r>0\) tal que\(S\) esté contenido en la bola abierta\(B^{n}(\mathbf{0}, r)\).

Equivalentemente, un conjunto\(S\) está acotado siempre y cuando haya una distancia fija\(r\) tal que ningún punto adentro\(S\) esté más alejado del origen que\(r\).

Ejemplo\(\PageIndex{1}\)

Cualquier bola abierta o cerrada\(\mathbb{R}^n\) es un conjunto acotado.

Ejemplo\(\PageIndex{2}\)

El rectángulo infinito

\[ \{(x, y): 1<x<3,-\infty<y<\infty\} \nonumber \]

no está acotada.

Teorema de Valor Extremo\(\PageIndex{1}\)

Supongamos que\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) es continuo en un conjunto abierto\(U\). Si\(S\) es un subconjunto cerrado y delimitado de\(U\), que\(f\) tiene un valor máximo y un valor mínimo on\(S\).

Dejamos la justificación de este teorema para un curso más avanzado.

Nuestro trabajo ahora es encontrar criterios para ubicar candidatos a puntos donde puedan ocurrir valores extremos locales, y luego clasificar estos puntos una vez que los hayamos encontrado. Para comenzar, supongamos que sabemos que\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) es diferenciable en un set abierto\(U\) y que tiene un valor extremo local en\(\mathbf{c}\). Entonces, para cualquier vector unitario\(\mathbf{u}\), la función\(g: \mathbb{R} \rightarrow \mathbb{R}\) definida por\(g(t)=f(\mathbf{c}+t \mathbf{u})\) debe tener un valor extremo at\(t=0\). Por lo tanto, a partir de un resultado en el cálculo de una variable, debemos tener

\[ 0=g^{\prime}(0)=D_{\mathbf{u}} f(\mathbf{c})=\nabla f(\mathbf{c}) \cdot \mathbf{u}. \nonumber \]

Ya que\(\mathbf{u}\) fue un vector unitario arbitrario en\(\mathbb{R}^n\), tenemos, en particular,

\[ 0=\nabla f(\mathbf{c}) \cdot \mathbf{e}_{k}=\frac{\partial}{\partial x_{i}} f(\mathbf{c}) \nonumber \]

para\(i=1,2, \cdots, n\). Es decir, debemos tener\(\nabla f(\mathbf{c})=\mathbf{0}\). Obsérvese que, por sí mismo,\(\nabla f(\mathbf{c})=\mathbf{0}\) sólo dice que la pendiente de la gráfica de\(f\) es 0 en la dirección de los vectores base estándar, pero esto de hecho implica que la pendiente es 0 en todas las direcciones porque\(D_{\mathbf{u}} f(\mathbf{c})=\nabla f(\mathbf{c}) \cdot \mathbf{u}\) para cualquier vector unitario\(\mathbf{u}\).

Teorema\(\PageIndex{1}\)

Si\(f: \mathbb{R}^{n} \longrightarrow \mathbb{R}\) es diferenciable en un conjunto abierto\(U\) y tiene un valor extremo local en\(\mathbf{c}\), entonces\(\nabla f(\mathbf{c})=\mathbf{0}\).

Definición\(\PageIndex{4}\)

Si\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) es diferenciable en\(\mathbf{c}\) y\(\nabla f(\mathbf{c})=\mathbf{0}\), entonces llamamos\(\mathbf{c}\) un punto crítico de\(f\). Llamamos a un punto\(\mathbf{c}\) en el que no\(f\) es diferenciable un punto singular de\(f\).

Recordemos que para encontrar los valores extremos de una función continua\(f: \mathbb{R} \rightarrow \mathbb{R}\) en un intervalo cerrado, solo necesitamos evaluar\(f\) en todos los puntos críticos y singulares dentro del intervalo así como en los puntos finales del intervalo, y luego inspeccionar estos valores para identificar los mayores y más pequeños. La historia es similar en la situación de una función\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) que se define en un conjunto cerrado y acotado\(S\) y es continua en algún conjunto abierto que contiene\(S\), excepto que en lugar de tener puntos finales a considerar, tenemos todo el límite de\(S\) a considerar.

Definición\(\PageIndex{5}\)

Deja\(S\) que sea un set en\(\mathbb{R}^n\). Llamamos a un punto\(\mathbf{a}\) en\(\mathbb{R}^n\) un punto límite de\(S\) si por cada\(r>0\), la bola abierta\(B^{n}(\mathbf{a}, r)\) contiene tanto los puntos dentro como\(S\) los puntos fuera de\(S\). Llamamos al conjunto de todos los puntos limítrofes\(S\) del límite de\(S\).

Ejemplo\(\PageIndex{3}\)

El límite del conjunto cerrado

\[ \bar{B}^{2}((0,0), 3)=\left\{(x, y): x^{2}+y^{2} \leq 9\right\} \nonumber \]

es el círculo

\[ S^{1}((0,0), 3)=\left\{(x, y): x^{2}+y^{2}=9\right\} . \nonumber \]

Ejemplo\(\PageIndex{4}\)

En general, el límite de la bola cerrada\(\bar{B}^{n}(\mathbf{a}, r)\) es la esfera\(S^{n-1}(\mathbf{a}, r)\).

Ejemplo\(\PageIndex{5}\)

El límite del rectángulo cerrado

\[ R=\{(x, y): 1 \leq x \leq 3,2 \leq y \leq 5\} \nonumber \]

consiste en los segmentos de línea de (1, 2) a (3, 2), (3, 2) a (3, 5), (3, 5) a (1, 5) y (1, 5) a (1, 2).

Ejemplo\(\PageIndex{6}\)

Supongamos que deseamos encontrar los valores extremos globales para la función\(f(x,y)=x^2+y^2\) en el conjunto cerrado

\[ D=\left\{(x, y): x^{2}+4 y^{2} \leq 4\right\} . \nonumber \]

Primero encontramos todos los puntos críticos y singulares. Ahora

\[ \nabla f(x, y)=(2 x, 2 y) , \nonumber \]

por lo

\[ \nabla f(x, y)=(0,0) \nonumber \]

si y solo si

\ [\ begin {alineado}
&2 x=0,\\
&2 y=0.
\ end {alineado}\]

De ahí que el único punto crítico es (0, 0). No hay puntos singulares, pero debemos considerar el límite de\(S\), la elipse

\[ B=\left\{(x, y): x^{2}+4 y^{2}=4\right\} . \nonumber \]

Ahora podemos usar

\[ \varphi(t)=(2 \cos (t), \sin (t)) , \nonumber \]

\(0 \leq t \leq 2 \pi\), para parametrizar\(B\). De ello se deduce que cualquier valor extremo de\(f\) ocurrir en también\(B\) será un valor extremo de

\ [\ begin {alineado}
g (t) &=f (\ varphi (t))\\
&=f (2\ cos (t),\ sin (t))\\
&=4\ cos ^ {2} (t) +\ sin ^ {2} (t)\\
&=4\ cos ^ {2} (t) +\ left (1-\ cos ^ {2} (t)\ derecha)\\
&=3\ cos ^ {2} (t) +1
\ end {alineado}\]

en el intervalo cerrado\([0,2 \pi]\). Ahora

\[ g^{\prime}(t)=-6 \cos (t) \sin (t) , \nonumber \]

por lo que los puntos críticos de\(g\) ocurren en puntos\(t\) en\((0,2 \pi )\) donde cualquiera\(\cos (t)=0\) o\(\sin (t)=0\). De ahí que los puntos críticos de\(g\) son\(t=\frac{\pi}{2}\),\(t=\pi\), y\(t=\frac{3 \pi}{2}\). Además, hay que considerar los puntos finales\(t=0\) y\(t=2 \pi \). De ahí que tengamos cuatro candidatos más para la ubicación de valores extremos, a saber,\(\varphi(0)=\varphi(2 \pi)=(2,0)\),\(\varphi\left(\frac{\pi}{2}\right)=(0,1)\),\(\varphi(\pi)=(-2,0)\), y\(\varphi\left(\frac{3 \pi}{2}\right)=(0,-1)\). Evaluando\(f\) en estos cinco puntos, tenemos

\ [\ begin {alineado}
&f (0,0) =0,\\
&f (2,0) =4,\\
&f (0,1) =1,\\
&f (-2,0) =4,
\ end {alineado}\]

y

\[ f(0,-1)=1 . \nonumber \]

Comparando estos valores, vemos que\(f\) tiene un valor máximo de 4 en (2, 0) y (−2, 0) y un valor mínimo de 0 en (0, 0). Ver Figura 3.5.1 para la gráfica de\(f\) en el conjunto\(D\).

Figura\(\PageIndex{1}\): Gráfico de\(f(x, y)=x^{2}+y^{2}\) on\(D=\left\{(x, y): x^{2}+4 y^{2} \leq 4\right\}\)

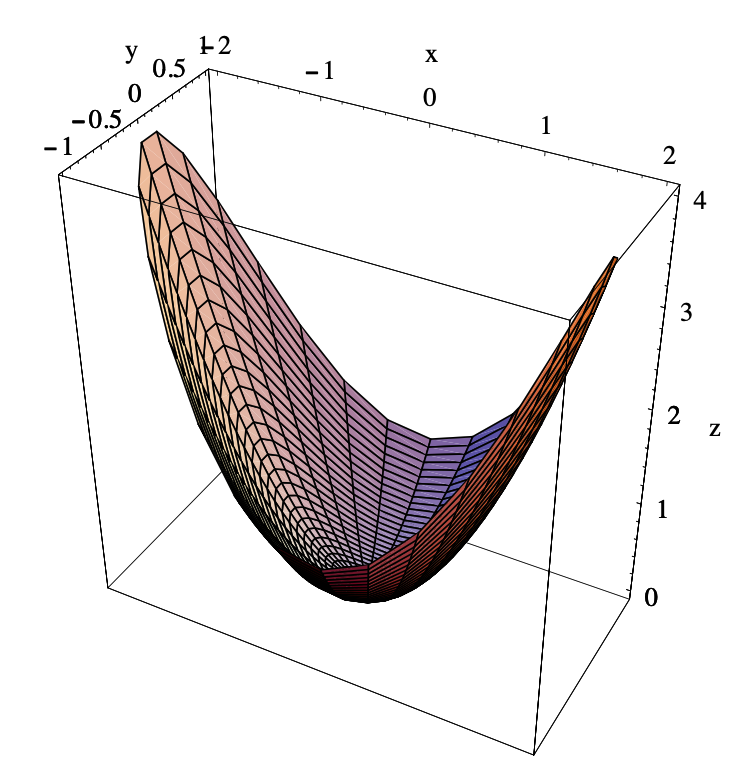
Como muestra el ejemplo anterior, tratar el límite de una región puede requerir una cantidad significativa de trabajo. En este ejemplo nos ayudó el hecho de que el límite era unidimensional y se parametrizó fácilmente. No siempre es así. Por ejemplo, el límite de la bola cerrada\(\bar{B}^{3}((0,0,0), 1)\) adentro\(\mathbb{R}^3\) es la esfera\(S^{2}((0,0,0), 1)\) con ecuación

\[ x^{2}+y^{2}+z^{2}=1, \nonumber \]

una superficie bidimensional. Veremos en el Capítulo 4 que es posible parametrizar tales superficies, pero eso aún nos dejaría con un problema bidimensional. Volveremos a este problema más adelante en esta sección cuando presentemos una solución mucho más elegante basada en nuestro conocimiento de conjuntos de niveles y vectores de gradiente.

Encontrar extrema local

Por ahora giraremos nuestra atención hacia la identificación de valores extremos locales. Recordemos de un cálculo variable que una de las formas más útiles para identificar un valor extremo local es a través de la segunda prueba derivada. Es decir, si\(c\) es un punto crítico de\(\varphi: \mathbb{R} \rightarrow \mathbb{R}\), entonces\(\varphi^{\prime \prime}(c)>0\) implica que\(\varphi\) tiene un mínimo local en\(c\) e\(\varphi^{\prime \prime}(c)<0\) implica\(\varphi\) tiene un máximo local at\(c\). El teorema de Taylor proporciona una manera fácil de ver por qué esto es así. Por ejemplo, supongamos que\(c\) es un punto crítico de\(\varphi\),\(\varphi^{\prime \prime}\) es continuo en un intervalo abierto que contiene\(c\), y\(\varphi^{\prime \prime}(c)>0\). Entonces hay un intervalo\(I=(c-r, c+r), r>0\), tal que\(\varphi^{\prime \prime}\) es continuo encendido\(I\) y\(\varphi^{\prime \prime}(t)>0\) para todos\(t\) adentro\(I\). Por el teorema de Taylor, para cualquiera\(h\) con\(|h|<r\), hay un número\(s\) entre\(c\) y\(c+h\) tal que

\[ \varphi(c+h)=\varphi(c)+\varphi^{\prime}(c) h+\frac{1}{2} \varphi^{\prime \prime}(s) h^{2}=\varphi(c)+\frac{1}{2} \varphi^{\prime \prime}(s) h^{2}>\varphi(c) , \]

donde hemos aprovechado el hecho de que\(\varphi^{\prime}(c)=0\) desde entonces\(c\) es un punto crítico de\(\varphi\). De ahí\(\varphi (c)\) que sea un valor mínimo local de\(\varphi\).

Consideraciones similares conducen a una segunda prueba derivada para una función\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\). Supongamos que\(\mathbf{c}\) es un punto crítico de\(f\),\(f\) está\(C^2\) en un conjunto abierto que contiene\(\mathbf{c}\), y\(H f(\mathbf{c})\) es positivo definido. Dejemos\(B^{n}(\mathbf{c}, r), r>0\), ser una bola abierta sobre la que\(f\) sea\(C^2\) y\(H f(\mathbf{c})\) sea positiva definitiva. Entonces, por la versión del teorema de Taylor en la Sección 3.4, para cualquiera\(\mathbf{h}\) con\(\|\mathbf{h}\|<r\), hay un número\(s\) entre 0 y 1 tal que

\[ f(\mathbf{c}+\mathbf{h})=f(\mathbf{c})+\nabla f(\mathbf{c}) \cdot \mathbf{h}+\frac{1}{2} \mathbf{h}^{T} H f(\mathbf{c}+s \mathbf{h}) \mathbf{h}=f(\mathbf{c})+\frac{1}{2} \mathbf{h}^{T} H f(\mathbf{c}+s \mathbf{h}) \mathbf{h}>f(\mathbf{c}) , \]

donde\(\nabla f(\mathbf{c})=\mathbf{0}\) ya\(\mathbf{c}\) es un punto crítico de\(f\), y la desigualdad final se deriva de la suposición que\(H f(\mathbf{x})\) es positiva definitiva para\(x\) in\(B^{n}(\mathbf{c}, r)\). De ahí\(f(\mathbf{c})\) que sea un valor mínimo local de\(f\). El mismo argumento muestra que si\(H f(\mathbf{c})\) es negativo definido, entonces\(f(\mathbf{c})\) es un valor máximo local de\(f\). Si\(H f(\mathbf{c})\) es indefinido, entonces habrá arbitrariamente pequeños\(\mathbf{h}\) para los cuales

\[ \frac{1}{2} \mathbf{h}^{T} H f(\mathbf{c}+s \mathbf{h}) \mathbf{h}>0 \nonumber \]

y arbitrariamente pequeños\(\mathbf{h}\) para los cuales

\[ \frac{1}{2} \mathbf{h}^{T} H f(\mathbf{c}+s \mathbf{h}) \mathbf{h}<0 . \nonumber \]

De ahí que habrá arbitrariamente pequeños\(\mathbf{h}\) para los cuales\(f(\mathbf{c}+\mathbf{h})>f(\mathbf{c})\) y arbitrariamente pequeños\(\mathbf{h}\) para los cuales\(f(\mathbf{c}+\mathbf{h})<f(\mathbf{c})\). En este caso, no\(f(\mathbf{c})\) es ni un mínimo local ni un máximo local. En este caso, llamamos punto\(\mathbf{c}\) de silla de montar. Por último, si\(H f(\mathbf{c})\) es indefinido, entonces no tenemos suficiente información para clasificar el punto crítico. Ahora podemos exponer la segunda prueba derivada.

Prueba de segunda derivada

Supongamos que\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) está\(C^2\) en un set abierto\(U\). Si\(\mathbf{c}\) es un punto crítico de\(f\) in\(U\), entonces\(f(\mathbf{c})\) es un valor mínimo local de\(f\) si\(H f(\mathbf{c})\) es positivo definido,\(f(\mathbf{c})\) es un valor máximo local de\(f\) si\(H f(\mathbf{c})\) es negativo definido, y\(\mathbf{c}\) es un punto de sillín si\(H f(\mathbf{c})\) es indefinido. Si\(H f(\mathbf{c})\) es indefinido, entonces se necesita más información para poder clasificar\(\mathbf{c}\).

El siguiente ejemplo da una indicación para la fuente del término punto de silla de montar.

Ejemplo\(\PageIndex{7}\)

Para encontrar los valores extremos locales de\(f(x, y)=x^{2}-y^{2}\), comenzamos por encontrar

\[ \nabla f(x, y)=(2 x,-2 y) . \nonumber \]

Ahora

\[ \nabla f(x, y)=(0,0) \nonumber \]

si y solo si

\ [\ begin {alineado}
2 x &=0,\\
-2 y &=0,
\ end {alineado}\]

que ocurre si y sólo si\(x=0\) y\(y=0\). Así\(f\) tiene el punto crítico único (0, 0). Ahora

\ [H f (x, y) =\ left [\ begin {array} {rr}
2 & 0\\
0 & -2
\ end {array}\ right],\ nonumber\]

por lo

\ [H f (0,0) =\ left [\ begin {array} {rr}
2 & 0\\
0 & -2
\ end {array}\ right]. \ nonumber\]

Así

\[ \operatorname{det}(H f(0,0))=(2)(-2)=-4<0 . \nonumber \]

De ahí que\(Hf(0,0)\) sea indefinido y así, por la segunda prueba derivada, (0, 0) es un punto de sillín. Mirando la gráfica de\(f\) en la Figura 3.5.2, podemos ver la razón de esto: ya que\(f(x, 0)=x^{2}\) y\(f(0, y)=-y^{2}\), la porción de la gráfica de\(f\) arriba del\(x\) eje -es una parábola que se abre hacia arriba mientras que la porción de la gráfica de\(f\) por encima del\(y\) eje -es una parábola que se abre hacia abajo.

Figura\(\PageIndex{2}\): Gráfica de\(f(x, y)=x^{2}-y^{2}\)

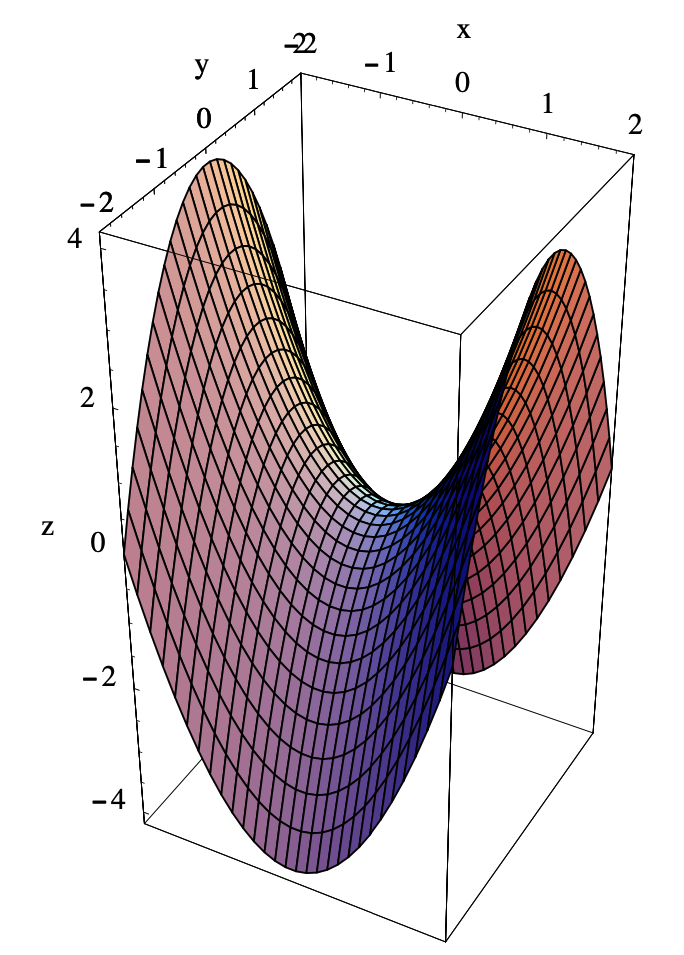
Ejemplo\(\PageIndex{8}\)

Considerar\(f(x, y)=x y e^{-\left(x^{2}+y^{2}\right)}\). Entonces

\[ \nabla f(x, y)=e^{-\left(x^{2}+y^{2}\right)}\left(y-2 x^{2} y, x-2 x y^{2}\right) . \nonumber \]

De ahí que, ya que\(e^{-\left(x^{2}+y^{2}\right)}>0\) para todos\((x,y)\),

\[ \nabla f(x, y)=(0,0) \nonumber \]

si y solo si

\ [\ begin {aligned}
&y-2 x^ {2} y=0,\\
&x-2 x y^ {2} =0,
\ end {alineado}\]

que ocurre si y solo si

\ [\ begin {aligned}
&y\ left (1-2 x^ {2}\ right) =0,\\
&x\ left (1-2 y^ {2}\ right) =0.
\ end {alineado}\]

Ahora la primera ecuación se satisface si cualquiera\(y=0\) o\(1-2 x^{2}=0\). Si\(y=0\), entonces la segunda ecuación se convierte\(x=0\), entonces (0, 0) es un punto crítico. Si\(1-2 x^{2}=0\), entonces cualquiera\(x=-\frac{1}{\sqrt{2}}\) o\(x=\frac{1}{\sqrt{2}}\). Para cualquiera de estos valores de\(x\), la segunda ecuación se satisface si y sólo si\(1-2 y^{2}=0\), es decir,\(y=-\frac{1}{\sqrt{2}}\) o\(y=\frac{1}{\sqrt{2}}\). De ahí que tengamos cuatro puntos críticos más:\(\left(-\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}\right),\left(-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right),\left(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}\right)\), y\(\left(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)\). Ahora

\ [H f (x, y) =e^ {-\ izquierda (x^ {2} +y^ {2}\ derecha)}\ izquierda [\ begin {array} {cc}
4 x^ {3} y-6 x y & 4 x^ {2} y^ {2} -2 x^ {2} -2 y^ {2} -2 y^ {2} +1\\
4 x^ {2} y^ {2} -2 x^ {2} -2 y^ {2} +1 y 4 y^ {3} x-6 x y
\ end {array}\ derecha],\ nonumber\]

por lo

\ [\ begin {reunió}
H f (0,0) =\ left [\ begin {array} {ll}
0 & 1\\
1 & 0
\ end {array}\ right],\\
H f\ left (-\ frac {1} {\ sqrt {2}}, -\ frac {1} {\ sqrt {2}}\ derecha) =H f\ izquierda (\ frac {1}} {\ sqrt {2}},\ frac {1} {\ sqrt {2}}\ derecha) =e^ {-1}\ izquierda [\ begin {array} {rr}
-2 & 0\\
0 y -2
\ end {array}\ derecha],
\ end {reunidos}\]

y

\ [H f\ izquierda (-\ frac {1} {\ sqrt {2}},\ frac {1} {\ sqrt {2}}\ derecha) =H f\ izquierda (\ frac {1} {\ sqrt {2}}, -\ frac {1} {\ sqrt {2}}\ derecha) =e^ {-1}\ izquierda [\ begin {array} ll}
2 & 0\\
0 & 2
\ end {array}\ right]. \ nonumber\]

Desde

\ [\ begin {reunió}
\ operatorname {det}\ left [\ begin {array} {ll}
0 & 1\\
1 & 0
\ end {array}\ right] =-1<0,\\
\ nombreoperador {det}\ left [\ begin {array} {cc}
-2 e^ {-1} & 0\\
0 & -2 e^ {-1}
\ end {array}\ right] =4 e^ {-2} >0,
\ end {reunidos}\]

y

\ [\ nombreoperador {det}\ left [\ begin {array} {cc}
2 e^ {-1} & 0\\
0 & 2 e^ {-1}
\ end {array}\ right] =4 e^ {-2} >0,\ nonumber\]

vemos que\(Hf(0,0)\) es indefinido,\(H f\left(-\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}\right)\) y\(H f\left(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)\) son negativos definidos,\(H f\left(-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)\) y\(H f\left(-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)\) son positivos definitivos. Así (0, 0) es un punto de silla de montar de\(f\),\(f\) tiene máximos locales de\(\frac{1}{2} e^{-1}\) en ambos\(\left(-\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}\right)\) y\(\left(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)\), y mínimos locales de\(-\frac{1}{2} e^{-1}\) at\(\left(-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)\) y\(\left(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}\right)\). Ver Figura 3.5.3.

Figura\(\PageIndex{3}\): Gráfica de\(f(x, y)=x y e^{-\left(x^{2}+y^{2}\right)}\)

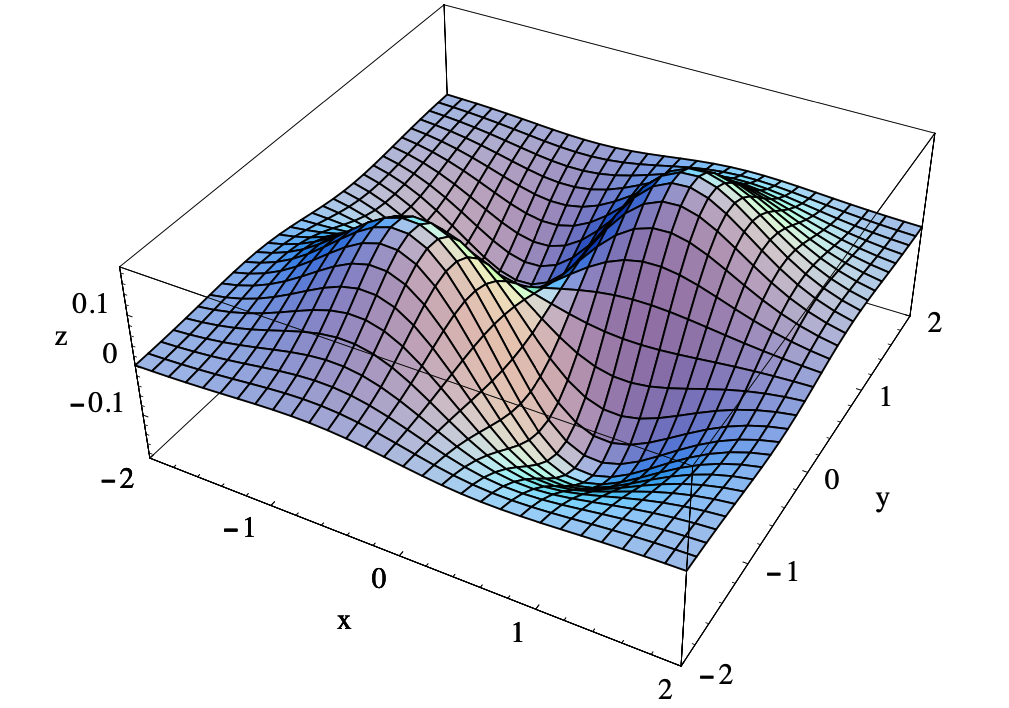
Encontrar los extremos globales

La gráfica de\(f(x, y)=x y e^{-\left(x^{2}+y^{2}\right)}\) la Figura 3.5.3 sugiere que los valores extremos locales encontrados en el ejemplo anterior son, de hecho, valores extremos globales para\(f\) todos\(\mathbb{R}^2\). Podemos verificar que este de hecho el caso de la siguiente manera. En primer lugar señalar que, desde

\[ \lim _{r \rightarrow \infty} r^{2} e^{-r^{2}}=0 , \nonumber \]

podemos elegir lo suficientemente\(R\) grande para que

\[ r^{2} e^{-r^{2}}<\frac{1}{2} e^{-1} \nonumber \]

cuando sea\(r \geq R\). Ahora para cualquier punto\((x,y)\) con\(\|(x, y)\|=r \geq R\) tenemos

\[ |f(x, y)|=\left|x y e^{-\left(x^{2}+y^{2}\right)}\right|=|x||y| e^{-\left(x^{2}+y^{2}\right)} \leq r^{2} e^{-r^{2}}<\frac{1}{2} e^{-1} . \nonumber \]

De ahí\(f(x,y)\) que esté entre\(-\frac{1}{2} e^{-1}\) y\(\frac{1}{2} e^{-1}\) para todos los puntos\((x,y)\) fuera del disco cerrado\(D=\bar{B}^{2}((0,0), R)\). Además, dado que\(f(x,y)\) es entre\(-\frac{1}{2} e^{-1}\) y\(\frac{1}{2} e^{-1}\) para todos los puntos\((x,y)\) en el límite de\(D\),\(f\) tiene un valor mínimo de\(-\frac{1}{2} e^{-1}\) y un valor máximo de\(\frac{1}{2} e^{-1}\) on\(D\). De ahí que estos valores sean en realidad los valores extremos globales de\(f\) en todos\(\mathbb{R}^2\).

Ejemplo\(\PageIndex{9}\)

Un agricultor desea construir un contenedor de almacenamiento rectangular, sin tapa, con un volumen de 500 metros cúbicos utilizando la menor cantidad de material posible. Si dejamos\(x\) y\(y\) ser las dimensiones de la base de la papelera y\(z\) ser la altura, todo medido en metros, entonces el agricultor desea minimizar la superficie de la papelera, dada por

\[ S=x y+2 x z+2 y z , \label{3.5.3} \]

con sujeción a la limitación del volumen, a saber,

\[ 500=x y z . \nonumber \]

Resolviendo\(z\) en esta última expresión y sustituyendo en to (\(\ref{3.5.3}\)), tenemos

\[ S=x y+2 x\left(\frac{500}{x y}\right)+2 y\left(\frac{500}{x y}\right)=x y+\frac{1000}{y}+\frac{1000}{x} . \nonumber \]

Esta es la función que necesitamos minimizar en el rectángulo abierto infinito

\[ R=\{(x, y): x>0, y>0\} . \nonumber \]

Ahora

\[ \frac{\partial S}{\partial x}=y-\frac{1000}{x^{2}} \nonumber \]

y

\[ \frac{\partial S}{\partial y}=x-\frac{1000}{y^{2}} \nonumber \]

así que para encontrar los puntos críticos de que\(S\) necesitamos resolver

\ [\ begin {alineado}
&y-\ frac {1000} {x^ {2}} =0,\\
&x-\ frac {1000} {y^ {2}} =0.
\ end {alineado}\]

Resolviendo para\(y\) en el primero de estos, tenemos

\[ y=\frac{1000}{x^{2}} , \nonumber \]

que, cuando se sustituye en el segundo, nos da

\[ x-\frac{x^{4}}{1000}=0 . \nonumber \]

De ahí que queremos

\[ x\left(1-\frac{x^{3}}{1000}\right)=0 , \nonumber \]

de lo que se deduce que\(x = 0\) o bien\(x = 10\). Ya que el primero de estos no nos va a dar un punto en\(R\), tenemos\(x = 10\) y

\[ y=\frac{1000}{10^{2}}=10 . \nonumber \]

Así, el único punto crítico es (10, 10). Ahora

\ [H S (x, y) =\ left [\ begin {array} {cc}
\ frac {2000} {x^ {3}} & 1\\
1 &\ frac {2000} {y^ {3}}
\ end {array}\ derecha],\ nonumber\]

por lo

\ [H S (10,10) =\ left [\ begin {array} {ll}
2 & 1\\
1 & 2
\ end {array}\ right]. \ nonumber\]

Así

\[ \operatorname{det}(H S(10,10))=3 , \nonumber \]

y así\(HS(10,10)\) es positivo definido. Esto demuestra que\(S\) tiene un mínimo local de

\[ \left.S\right|_{x=10, y=10}=(10)(10)+\frac{1000}{10}+\frac{1000}{10}=300 \nonumber \]

en\((x, y)=(10,10)\). Para demostrar que este es en realidad el valor mínimo global de\(S\), procedemos de la siguiente manera. Dejar\(D\) ser el rectángulo cerrado

\[ D=\{(x, y): 1 \leq x \leq 400,1 \leq y \leq 400\} . \nonumber \]

Ahora si\(0<x \leq 1\), entonces

\[ \frac{1000}{x} \geq 1000 , \nonumber \]

y así\(S > 300\). Del mismo modo, si\(0<y \leq 1\), entonces\(S > 300\). Además, si\(x \geq 400\) y\(y \geq 1\), entonces\(xy \geq 400\), y así\(S > 300\). Del mismo modo, si\(y \geq 400\) y\(x \geq 1\), entonces\(S > 300\). De ahí que\(S > 300\) para todos\((x,y)\) fuera de\(D\) y para todos\((x,y)\) en el límite de\(D\). De ahí que\(S\) tenga un mínimo global de 300 on\(D\), que, a partir de las observaciones anteriores, debe de hecho ser el mínimo global de\(S\) en todos\(R\). Consulte la gráfica de\(S\) la Figura 3.5.4. Por último, cuando\(x=10\) y\(y=10\), tenemos

\[ z=\frac{500}{(10)(10)}=5 , \nonumber \]

por lo que el agricultor debe construir su papelera para tener una base de 10 metros por 10 metros y una altura de 5 metros.

Figura\(\PageIndex{4}\): Gráfica de\(S=x y+\frac{1000}{x}+\frac{1000}{y}\)

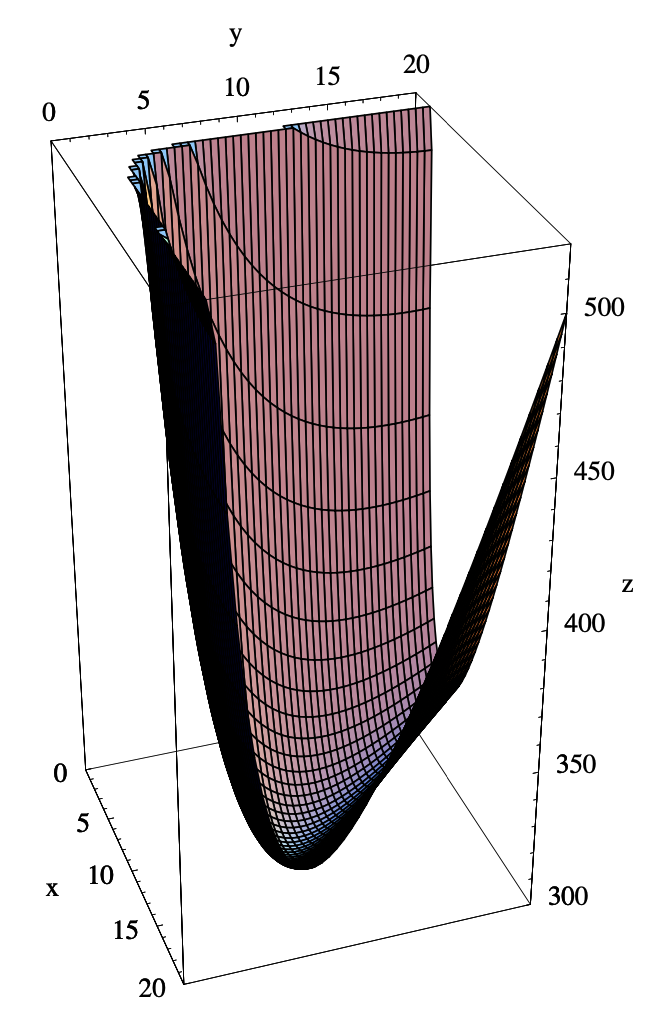
Multiplicadores Lagrange

Este último ejemplo tiene mucho en común con nuestro primer ejemplo en el sentido de que ambos implican encontrar valores extremos de una función restringida a un subconjunto de dimensiones inferiores. En nuestro primer ejemplo, tuvimos que encontrar los valores extremos de\(f(x, y)=x^{2}+y^{2}\) restringido a la elipse unidimensional con ecuación\(x^{2}+4 y^{2}=4\); en el ejemplo que acabamos de terminar, tuvimos que encontrar el valor mínimo de\(S=x y+2 x z+2 y z\), una función de tres variables, restringido a la superficie bidimensional definido por la ecuación\(xyz = 500\). A pesar de que eran similares, abordamos estos problemas de manera algo diferente. En el primero, parametrizamos la elipse y luego maximizamos la composición de\(f\) con esta parametrización; en la segunda, resolvimos para\(z\) en términos de\(x\) y\(y\) y luego sustituimos en la fórmula para\(S\) para hacer\(S\) efectivamente una función de dos variables. Ahora vamos a describir un enfoque general que se aplica a ambas situaciones. Muchas veces, pero no siempre, este método es más fácil de aplicar que las otras dos técnicas. En la práctica, se intenta seleccionar el método que dará una respuesta con la menor resistencia.

Para el caso general, considerar dos funciones diferenciables,\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) y\(g: \mathbb{R}^{n} \rightarrow \mathbb{R}\), y supongamos que deseamos encontrar los valores extremos de\(f\) en el nivel establecido\(S\) de\(g\) determinado por la restricción\(g(\mathbf{x})=0\). Si\(f\) tiene un valor extremo en un punto\(\mathbf{c}\) encendido\(S\), entonces\(f(\mathbf{c})\) debe ser un valor extremo\(f\) a lo largo de cualquier curva que pase a través\(\mathbf{c}\). Por lo tanto, si\(\varphi: \mathbb{R} \rightarrow \mathbb{R}^{n}\) parametriza una curva en\(S\) con\(\varphi(b)=\mathbf{c}\), entonces la función\(h(t)=f(\varphi(t))\) tiene un valor extremo en\(b\). De ahí

\[ 0=h^{\prime}(b)=\nabla f(\varphi(b)) \cdot D \varphi(b)=\nabla f(\mathbf{c}) \cdot D \varphi(b) . \label{3.5.4} \]

Dado que (\(\ref{3.5.4}\)) se mantiene para cualquier curva en\(S\) a través\(\mathbf{c}\) y\(D \varphi(b)\) es tangente a la curva dada en\(\mathbf{c}\), se deduce que\(\nabla f(\mathbf{c})\) es ortogonal al hiperplano tangente a\(S\) at\(\mathbf{c}\). Pero\(S\) es un conjunto de niveles de\(g\), por lo que sabemos por nuestro trabajo en la Sección 3.3 que el vector\(\nabla g(\mathbf{c})\), siempre que sea distinto de cero, es un vector normal para el hiperplano tangente a\(S\) at\(\mathbf{c}\). De ahí que\ nabla f (\ mathbf {c}) y\ nabla g (\ mathbf {c}) deben ser paralelos. Es decir, debe existir un escalar\(\lambda\) tal que

\[ \nabla f(\mathbf{c})=\lambda \nabla g(\mathbf{c}) . \]

La idea ahora es que al buscar valores extremos, solo necesitamos considerar puntos\(\mathbf{c}\) para los que\(g(\mathbf{c})=0\) tanto como\(\nabla f( \mathbf{c} )= \lambda \nabla g( \mathbf{c} ) \) para algunos escalares\( \lambda \). El escalar\( \lambda \) se conoce como multiplicador Lagrange, y este método para encontrar valores extremos sujetos a una ecuación restrictiva se conoce como el método de los multiplicadores Lagrange.

Ejemplo\(\PageIndex{10}\)

Supongamos que la temperatura en un punto\((x,y,z)\) de la esfera unitaria\(S =S^{2}((0,0,0), 1)\) viene dada por

\[ T(x, y, z)=30+5(x+z) . \nonumber \]

Para encontrar los valores extremos de\(T\), primero definimos

\[ g(x, y, z)=x^{2}+y^{2}+z^{2}-1, \nonumber \]

haciendo así\(S\) la superficie nivelada de\(g\) especificado por\(g(x,y,z) = 0\). Ahora

\[ \nabla f(x, y, z)=(5,0,5) \nonumber \]

y

\[ \nabla g(x, y, z)=(2 x, 2 y, 2 z) . \nonumber \]

Los candidatos para las ubicaciones de valores extremos serán soluciones de las ecuaciones

\ [\ comenzar {alineado}
\ nabla f (x, y, z) &=\ lambda\ nabla g (x, y, z),\\
g (x, y, z) &=0,
\ end {alineado}\]

es decir,

\ [\ begin {alineado}
& (5,0,5) =\ lambda (2 x, 2 y, 2 z),\\
&x^ {2} +y^ {2} +z^ {2} -1=0.
\ end {alineado}\]

De ahí que necesitamos resolver el siguiente sistema de cuatro ecuaciones en cuatro incógnitas:

\ [\ begin {reunió}
5=2\ lambda x,\\
0=2\ lambda y,\\
5=2\ lambda z,\\
x^ {2} +y^ {2} +z^ {2} =1.
\ end {reunido}\]

Ahora\(5 = 2 \lambda x\) implica eso\(\lambda \neq 0,\) y así\(0=2 \lambda y\) implica eso\(y=0\). Por otra parte,\(5 = 2 \lambda x\) e\(5 = 2 \lambda z\) implicar eso\(2 \lambda x = 2 \lambda z \), de lo que se desprende, ya que\(\lambda \neq 0,\), eso\(x=z\). Sustituyendo estos resultados en la ecuación final, tenemos

\[ 1=x^{2}+y^{2}+z^{2}=x^{2}+0+x^{2}=2 x^{2} . \nonumber \]

Así\( x=-\frac{1}{\sqrt{2}} \) o\(x=\frac{1}{\sqrt{2}}\), y tenemos dos soluciones para nuestras ecuaciones,

\[ \left(-\frac{1}{\sqrt{2}}, 0,-\frac{1}{\sqrt{2}}\right) \nonumber \]

y

\[ \left(\frac{1}{\sqrt{2}}, 0, \frac{1}{\sqrt{2}}\right) \nonumber \]

En este punto, dado que\(T\) es continuo y\(S\) está cerrado y acotado, sólo necesitamos evaluar\(T\) en estos puntos y comparar sus valores. Ahora

\[ T\left(-\frac{1}{\sqrt{2}}, 0,-\frac{1}{\sqrt{2}}\right)=30-5 \sqrt{2}=22.93 \nonumber \]

y

\[ T\left(\frac{1}{\sqrt{2}}, 0, \frac{1}{\sqrt{2}}\right)=30+5 \sqrt{2}=37.07 , \nonumber \]

donde los valores finales se han redondeado a dos decimales, por lo que la temperatura máxima en la esfera es 37.07 a\(\left(\frac{1}{\sqrt{2}}, 0, \frac{1}{\sqrt{2}}\right)\) y la temperatura mínima es 22.93 at\(\left(-\frac{1}{\sqrt{2}}, 0,-\frac{1}{\sqrt{2}}\right)\).

Ejemplo\(\PageIndex{11}\)

Supongamos que el agricultor en nuestro ejemplo anterior se enfrenta al problema opuesto: Dados los 300 metros cuadrados de material, ¿cuáles son las dimensiones de la papelera rectangular, sin tapa, que contiene el mayor volumen? Si volvemos a dejar\(x\) y\(y\) ser las dimensiones de la base de la papelera y\(z\) ser su altura, entonces queremos maximizar

\[ V=x y z \nonumber \]

sobre la región donde\(x>0, y>0\), y\(z>0\), con sujeción a la restricción de que

\[ x y+2 x z+2 y z=300 . \nonumber \]

Si dejamos

\[ g(x, y, z)=x y+2 x z+2 y z-300 , \nonumber \]

entonces nuestro problema es maximizar\(V\) sujeto a la restricción\(g(x, y, z)=0\). Ahora

\[ \nabla V=(y z, x z, x y) \nonumber \]

y

\[ \nabla g(x, y, z)=(y+2 z, x+2 z, 2 x+2 y) , \nonumber \]

por lo que el sistema de ecuaciones

\ [\ comenzar {reunido}
\ nabla V=\ lambda\ nabla g (x, y, z),\\
g (x, y, z) =0,
\ final {reunido}\]

se convierte en el sistema

\ [\ begin {align}
y z=\ lambda (y+2 z),\ label {3.5.6}\\
x z=\ lambda (x+2 z),\ etiqueta {3.5.7}\\
x y=\ lambda (2 x+2 y),\ etiqueta {3.5.8}\\
x y+2 x z+2 y z=300. \ label {3.5.9}
\ end {align}\]

Las ecuaciones (\(\ref{3.5.6}\)) y (\(\ref{3.5.7}\)) implican que

\[ \lambda=\frac{y x}{y+2 z} \nonumber \]

y

\[ \lambda=\frac{x z}{x+2 z} , \nonumber \]

por lo

\[ \frac{y z}{y+2 z}=\frac{x z}{x+2 z} , \nonumber \]

es decir,

\[ \frac{y}{y+2 z}=\frac{x}{x+2 z} . \nonumber \]

De ahí

\[ x y+2 y z=x y+2 x z . \nonumber \]

Así\(2 y z=2 x z\), así\(x=y\). Sustituir este resultado en (\(\ref{3.5.8}\)) nos da\(x^{2}=4 \lambda x\), de lo que se deduce que\( x = 4 \lambda \). Sustituyendo en (\(\ref{3.5.7}\)), tenemos

\[ 4 \lambda z=\lambda(4 \lambda+2 z)=4 \lambda^{2}+2 \lambda z . \nonumber \]

De ahí\(2 \lambda z=4 \lambda^{2}\), así\(z = 2 \lambda \). Poner\( x = 4 \lambda \),\( y = 4 \lambda \), y\(z = 2 \lambda \) en (\(\ref{3.5.9}\)) produce la ecuación

\[ 16 \lambda^{2}+16 \lambda^{2}+16 \lambda^{2}=300 . \nonumber \]

Por lo tanto\(48 \lambda^{2}=300\), así

\[ \lambda=\pm \sqrt{\frac{300}{48}}=\pm \sqrt{\frac{25}{4}}=\pm \frac{5}{2} . \nonumber \]

Ahora\(x\),\(y\), y todos\(z\) son positivos, así que debemos tener\(\lambda=\frac{5}{2}\), dándonos\(x=10\),\(y=10\), y\(z=5\). Para demostrar que tenemos la ubicación del valor máximo de\(V\), vamos

\[ S=\{(x, y, z): g(x, y, z)=0, x>0, y>0, z>0\} \nonumber \]

y que\(D\) sea esa parte de\(S\) para la cual\( 1 \leq x \leq 150\),\( 1 \leq y \leq 150\), y\( 1 \leq z \leq 150\). Tenga en cuenta que si\((x,y,z)\) se encuentra en\(S\), entonces

\[ 300=x y+2 x z+2 y z \nonumber \]

y así\( xy \leq 300\),\( xz \leq 150\), y\( yz \leq 150\). Además,

\[ z=\frac{300-x y}{2 x+2 y} . \nonumber \]

Ahora bien, si cualquiera\( x \geq 150\) o\( y \geq 150\), entonces

\[ z \leq \frac{300}{300} \leq 1 , \nonumber \]

por lo

\[ V=x y z \leq(300)(1)=300 . \nonumber \]

Si\(x \leq 1\),

\[ V=x y z \leq(1)(150)=150 \nonumber \]

y, análogamente, si\(y \leq 1 \),

\[ V=y x z \leq(1)(150)=150 . \nonumber \]

Por lo tanto, si\((x,y,z)\) está en el límite de\(D\) o fuera de\(D\), entonces\(V \leq 300\). Desde

\[ \left.V\right|_{(x, y, z)=(10,10,5)}=500 , \nonumber \]

se deduce que el máximo global de\(V\) on\(S\) debe ocurrir en su interior\(D\). De hecho, este valor máximo debe ser de 500 metros cúbicos, ocurriendo cuando\(x=10\)\(y=10\) metros, metros y\(z=5\) metros.