3.7: Cambio de variables en integrales definidas

Una de las técnicas básicas para evaluar una integral en el cálculo de una variable es la sustitución, reemplazando una variable por otra de tal manera que la integral resultante sea de una forma más simple. Aunque un poco más sutil en el caso de dos o más variables, una idea similar proporciona una técnica poderosa para evaluar integrales definidas.

Cambio lineal de variables

Presentaremos la idea principal a través de un ejemplo. Let

\[ D=\left\{(x, y): 9 x^{2}+4 y^{2} \leq 36\right\} , \nonumber \]

la región dentro de la elipse que interseca el\(x\) eje en (−2, 0) y (2, 0) y el\(y\) eje -en (0, −3) y (0, 3). Para encontrar el área de\(D\), evaluamos

\[ \iint_{D} d x d y=\int_{-2}^{2} \int_{-\frac{3}{2} \sqrt{4-x^{2}}}^{\frac{3}{2} \sqrt{4-x^{2}}} d y d x=\int_{-2}^{2} 3 \sqrt{4-x^{2}} d x=6 \pi , \nonumber \]

donde la integral final pueda evaluarse utilizando la sustitución\(x=2 \sin (\theta)\) o señalando que

\[ \int_{-2}^{2} \sqrt{4-x^{2}} d x \nonumber \]

es la mitad del área de un círculo de radio 2. Alternativamente, supongamos que escribimos la ecuación de la elipse como

\[ \frac{x^{2}}{4}+\frac{y^{2}}{9}=1 \nonumber \]

y hacer la sustitución\(x=2u\) y\(y=3v\). Entonces\(u = \frac{x}{2} \) y\(v = \frac{y}{3} \), entonces si\((x,y)\) es un punto en\(D\), entonces

\[ u^{2}+v^{2}=\frac{x^{2}}{4}+\frac{y^{2}}{9} \leq 1 . \nonumber \]

Es decir, si\((x,y)\) es un punto adentro\(D\), entonces\((u,v)\) es un punto en el disco de la unidad

\[ E=\left\{(u, v): u^{2}+v^{2} \leq 1\right\} . \nonumber \]

Por el contrario, si\((u,v)\) es un punto en\(E\), entonces

\[ \frac{x^{2}}{4}+\frac{y^{2}}{9}=\frac{4 u^{2}}{4}+\frac{9 v^{2}}{9}=u^{2}+v^{2} \leq 1 , \nonumber \]

así\((x,y)\) es un punto en\(D\). Así la función\(F(u, v)=(2 u, 3 v)\) toma la región\(E\), un disco cerrado de radio 1, y la estira sobre la región\(D\) (como se muestra en la Figura 3.7.1).

Figura\(\PageIndex{1}\):\(F\) mapas\(E\) en\(D\)

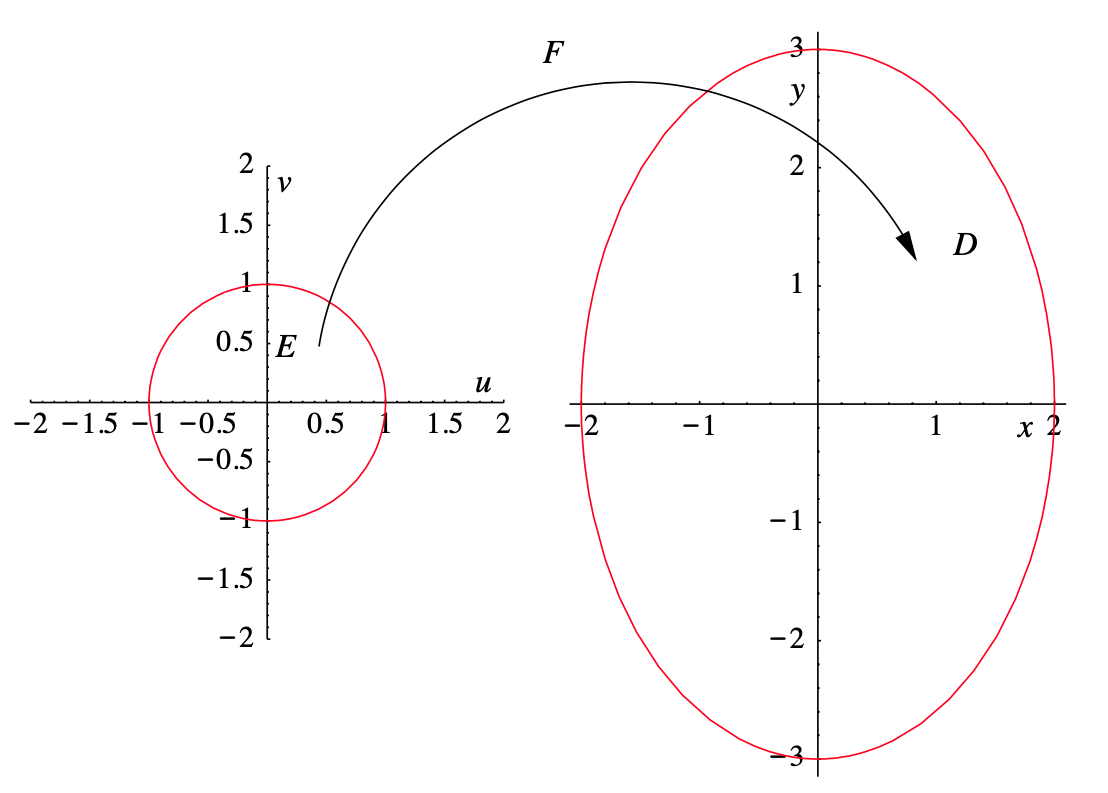
Sin embargo, tenga en cuenta que a pesar de que cada punto en\(E\) corresponde exactamente a un punto en\(D\), y, a la inversa, cada punto en\(D\) corresponde exactamente a punto en\(E\), sin embargo\(E\) y\(D\) no tienen la misma zona. Para ver cómo\(F\) cambia de área, considera qué le hace a la unidad cuadrada\(S\) con lados\(\mathbf{e}_{1}=(1,0)\) y\(\mathbf{e}_{2}=(0,1)\). El área de\(S\) es 1, pero se\(F\) \(S\)mapea en un rectángulo\(R\) con lados

\[ F(1,0)=(2,0) \nonumber \]

y

\[ F(0,1)=(0,3) \nonumber \]

y área 6. Este es un caso especial de un hecho general que vimos en la Sección 1.6: la función lineal\(F\), con matriz asociada

\ [M=\ left [\ begin {array} {ll}
2 & 0\\
0 & 3
\ end {array}\ right],\ nonumber\]

mapea el cuadrado de la unidad\(S\) en un paralelogramo\(R\) con área

\[ |\operatorname{det}(M)|=6 . \nonumber \]

El dato importante para nosotros aquí es que 1 unidad de área en el\(uv\) plano corresponde a 6 unidades de área en el\(xy\) plano. De ahí que el área de\(D\) será 6 veces el área de\(E\). Es decir,

\[ \iint_{D} d x d y=\iint_{E}|\operatorname{det}(M)| d u d v=\iint_{E} 6 d u d v=6 \iint_{E} d u d v=6 \pi , \nonumber \]

donde la integral final es simplemente el área dentro de un círculo de radio 1.

Estas ideas proporcionan el trasfondo para una prueba del siguiente teorema.

Teorema\(\PageIndex{1}\)

Supongamos que\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) es continuo en un conjunto abierto\(U\) que contiene el conjunto delimitado cerrado\(D\). Supongamos que\(F: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}\) es una función lineal,\(M\) es una\(n \times n\) matriz tal que\(F(\mathbf{u})=M \mathbf{u}\), y\(\operatorname{det}(M) \neq 0\). Si\(F\) mapea la región\(E\) a la región\(D\) y definimos el cambio de variables

\ [\ left [\ begin {array} {c}
x_ {1}\\
x_ {2}\\
\ vdots\\
x_ {n}
\ end {array}\ right] =M\ left [\ begin {array} {c}
u_ {1}\\
u_ {2}\\
\ vdots\\
u_ {n}
\ end {array}\ right],\ nonumber\]

entonces

\ [\ begin {align}
\ iint\ cdots\ int_ {D} f\ left (x_ {1}, x_ {2},\ ldots, x_ {n}\ derecha) d x_ {1} d x_ {2}\ cdots d x_ {n}\ nonumber\\
&=\ iint\ cdots\ int_ {E} f\ left (F\ izquierda (u_ {1}, u_ {2},\ ldots, u_ {n}\ derecha)\ derecha) |\ nombreoperador {det} (M) | d u_ {1} d u_ {2}\ cdots d u_ {n}\ etiqueta {3.7.1}
\ end {align}.\]

Ejemplo\(\PageIndex{1}\)

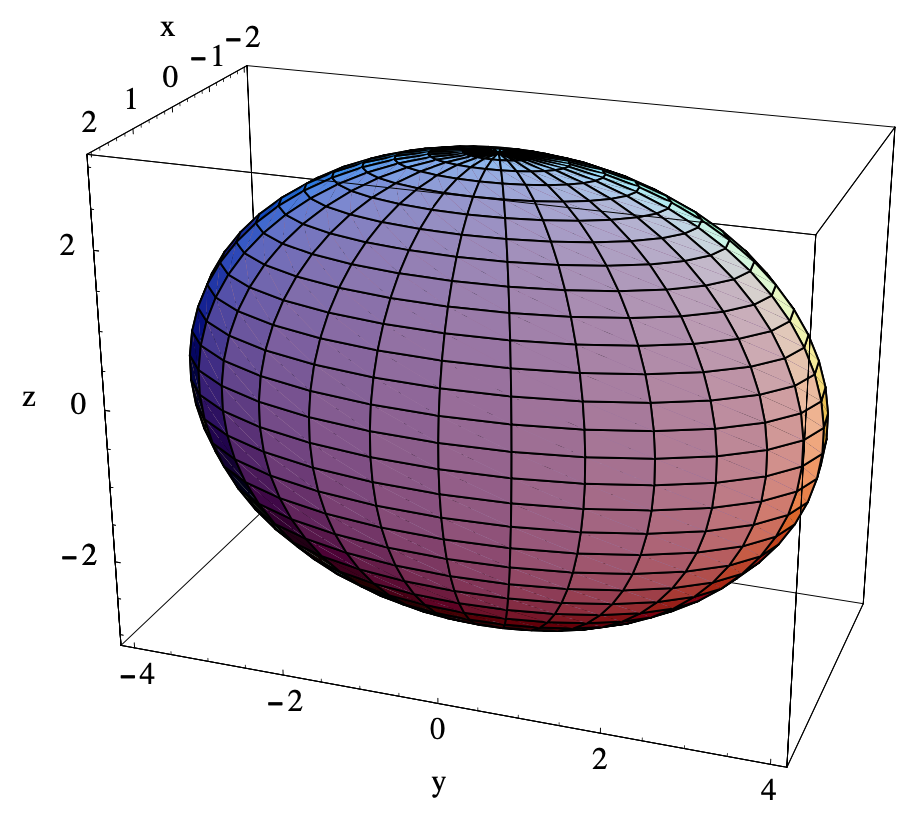
Dejar\(D\) ser la región en\(\mathbb{R}^3\) delimitada por el elipsoide con ecuación

\[ \frac{x^{2}}{4}+\frac{y^{2}}{16}+\frac{z^{2}}{9}=1 . \nonumber \]

Ver Figura 3.7.2.

Figura\(\PageIndex{2}\): El elipsoide\(\frac{x^{2}}{4}+\frac{y^{2}}{16}+\frac{z^{2}}{9}=1\)

Si hacemos el cambio de variables\(x = 2u, y = 4v\), y\(z = 3w\), es decir,

\ [\ left [\ begin {array} {l}
x\\
y\\
z
\ end {array}\ right] =\ left [\ begin {array} {lll}
2 & 0 & 0\\
0 & 4 & 0\\
0 & 0 & 0 & 3
\ end {array}\ right]\ left [\ begin {array} {c}
u\\
v\\
w
\ end {array}\ derecha],\ nonumber\]

entonces, para cualquiera\((x,y,z)\) en\(D\), tenemos

\[ u^{2}+v^{2}+w^{2}=\frac{x^{2}}{4}+\frac{y^{2}}{16}+\frac{z^{2}}{9} \leq 1 . \nonumber \]

Es decir, si\((x,y,z)\) yace adentro\(D\), entonces el correspondiente\((u,v,w)\) yace en la bola unitaria cerrada\(E=\bar{B}^{3}((0,0,0), 1)\). Por el contrario, si\((u,v,w)\) se encuentra en\(E\), entonces

\[ \frac{x^{2}}{4}+\frac{y^{2}}{16}+\frac{z^{2}}{9}=\frac{4 u^{2}}{4}+\frac{16 v^{2}}{16}+\frac{9 w^{2}}{9}=u^{2}+v^{2}+w^{2} \leq 1 , \nonumber \]

así\((x,y,z)\) se encuentra en\(D\). De ahí que el cambio de variables\(E\) se\(F(u, v, w)=(2 u, 4 v, 3 w)\) mapee sobre\(D\). Ahora

\ [\ nombreoperador {det}\ left [\ begin {array} {lll}
2 & 0 & 0\\
0 & 4 & 0\\
0 & 0 & 0 & 3
\ end {array}\ right] =24,\ nonumber\]

así que si\(V\) es el volumen de\(D\), entonces

\[ V=\iiint_{D} d x d y d z=\iiint_{E} 24 d u d v d w=24 \iiint_{E} d u d v d w=24\left(\frac{4 \pi}{3}\right)=32 \pi , \nonumber \]

donde hemos utilizado el hecho de que el volumen de una esfera de radio 1 es\( \frac{4 \pi }{3} \) para evaluar la integral final.

Cambio no lineal de variables

Sin entrar en los detalles técnicos, indicaremos cómo proceder cuando el cambio de variables no sea lineal. Supongamos que\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) es continuo en un conjunto abierto\(U\) que contiene el conjunto delimitado cerrado\(D\) y\(F: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}\) mapea una región delimitada cerrada\(E\) de\(\mathbb{R}^n\) on de\(D\) modo que cada punto de \(D\)corresponde exactamente a un punto de\(E\). Escribiendo\(F(\mathbf{u})=\left(F_{1}(\mathbf{u}), F_{2}(\mathbf{u}), \ldots, F_{n}(\mathbf{u})\right) \), vamos a suponer que\(F_{1}, F_{2}, \ldots,\) y todos\(F_n\) son diferenciables en un conjunto abierto\(W\) que contiene\(E\). Aunque no estudiaremos este tipo de función hasta el Capítulo 4, el candidato natural para la derivada de\(F\) es la matriz cuya fila es\(i\) th\(\nabla F_{i}(\mathbf{u})\). Dejando\(x_{i}=F_{i}\left(u_{1}, u_{2}, \ldots, u_{n}\right)\)\(i=1,2, \ldots, n\),, denotamos esta matriz, llamada la matriz jacobiana de\(F\),

\[ \frac{\partial\left(x_{1}, x_{2}, \ldots, x_{n}\right)}{\partial\left(u_{1}, u_{2}, \ldots, u_{n}\right)} . \]

De manera explícita,

\ [\ frac {\ parcial\ izquierda (x_ {1}, x_ {2},\ ldots, x_ {n}\ derecha)} {\ parcial\ izquierda (u_ {1}, u_ {2},\ ldots, u_ {n}\ derecha)} =\ izquierda [\ begin {array} {cccc}
\ frac {\ parcial} {\ parcial} {\ parcial u_ {}} F_ {1} (\ mathbf {u}) &\ frac {\ parcial} {\ parcial u_ {2}} F_ {1} (\ mathbf {u}) &\ cdots &\ frac {\ parcial} {\ parcial} {\ parcial u_ {n}} F_ {1} (\ mathbf {u})\
\ frac {\ parcial} {\ parcial u_ {1}} F_ {2} (\ mathbf {u}) &\ frac {\ parcial} {\ parcial} {\ parcial u_ {2}} F_ {2} (\ mathbf {u}) &\ cdots &\ frac {\ parcial} {\ parcial} {n}} F_ {2} (\ mathbf {u})\\
\ vdots &\ vdots &\ ddots &\ vdots\\
\ frac {\ parcial} {\ parcial u_ { 1}} F_ {n} (\ mathbf {u}) &\ frac {\ parcial} {\ parcial} {\ parcial u_ {2}} F_ {n} (\ mathbf {u}) &\ cdots &\ frac {\ parcial} {\ parcial} {n}} F_ {n} (\ mathbf {u})
\ end {array}\ derecho].

Veremos en el Capítulo 4 que

\[ \frac{\partial\left(x_{1}, x_{2}, \ldots, x_{n}\right)}{\partial\left(u_{1}, u_{2}, \ldots, u_{n}\right)} \nonumber \]

es la matriz para la parte lineal de la mejor aproximación afín a\(F\) at\(\left(u_{1}, u_{2}, \ldots, u_{n}\right)\). Por lo tanto, para rectángulos suficientemente pequeños, el factor por el cual\(F\) cambia el área de un rectángulo cuando lo mapea a una región será aproximadamente

\[ \left|\operatorname{det} \frac{\partial\left(x_{1}, x_{2}, \ldots, x_{n}\right)}{\partial\left(u_{1}, u_{2}, \ldots, u_{n}\right)}\right| . \]

Entonces se puede demostrar que, de manera análoga a (\(\ref{3.7.1}\)), tenemos

\ [\ begin {align}
\ int\ cdots &\ iint_ {D} f\ left (x_ {1}, x_ {2},\ ldots, x_ {n}\ derecha) d x_ {1} d x_ {2}\ cdots d x_ {n}\ nonumber\\
&=\ int\ cdots\ iint_ {E} f\ left (F\ izquierda (u_ {1}, u_ {2},\ ldots, u_ {n}\ derecha)\ derecha)\ izquierda|\ nombreoperador {det}\ frac {\ parcial\ izquierda (x_ {1}, x_ {2},\ lpuntos, x_ { n}\ derecha)} {\ parcial\ izquierda (u_ {1}, u_ {2},\ ldots, u_ {n}\ derecha)}\ derecha| d u_ {1} d u_ {2}\ cdots d u_ {n}. \ label {3.7.5}
\ end {align}\]

Tenga en cuenta que (\(\ref{3.7.5}\)) es justo (\(\ref{3.7.1}\)) con la matriz\(M\) reemplazada por la jacobiana de\(F\).

Ahora veremos dos casos especiales muy útiles del resultado anterior. Consulta los Ejercicios 22 y 23 para un tercer caso especial.

Coordenadas polares

Como alternativa a describir la ubicación de un punto\(P\) en el plano usando sus coordenadas cartesianas\((x,y)\), podemos ubicar el punto usando\(r\), la distancia desde\(P\) el origen, y\(\theta\), el ángulo entre el vector desde (0, 0) a\(P\) y el\(x\) eje positivo, medidos en sentido contrario a las agujas del reloj de 0 a\(2 \pi \) (ver Figura 3.7.3).

Figura\(\PageIndex{3}\): Coordenadas polares y cartesianas para un punto\(P\)

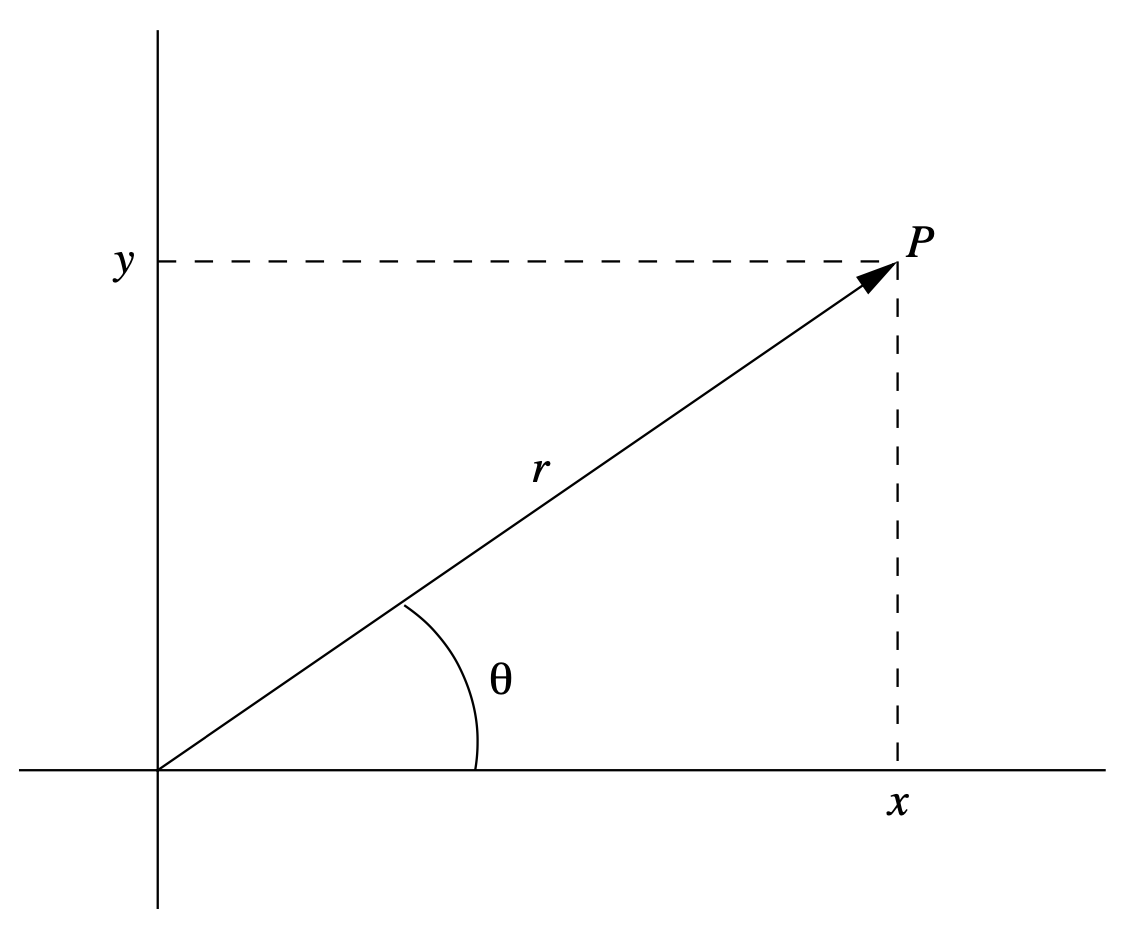
Es decir, si\(P\) tiene coordenadas cartesianas\((x,y)\)\(x \neq 0\), con, podemos definir sus coordenadas polares\((r, \theta )\) especificando que

\[ r=\sqrt{x^{2}+y^{2}} \]

y

\[ \tan (\theta)=\frac{y}{x} , \]

donde llevamos\(0 \leq \theta \leq \pi\) si\(y \geq 0\) y\(\pi<\theta<2 \pi\) si\(y<0\). Si\(x=0\), dejamos\(\theta = \frac{\pi}{2}\) si\(y>0\) y\( \theta = \frac{3 \pi}{2}\) si\(y<0\). Para\((x, y)=(0,0), r=0\) y\(\theta\) podría tener cualquier valor, y así es indefinido. Por el contrario, si un punto\(P\) tiene coordenadas polares\((r, \theta )\), entonces

\[ x=r \cos (\theta) \]

y

\[ y=r \sin (\theta) . \]

Tenga en cuenta que la elección del intervalo\( [0,2 \pi) \) para los valores de no\(\theta\) es única, con cualquier intervalo de longitud\(2 \pi \) funcionando también. Aunque\( [0,2 \pi) \) es la opción más común para los valores de\(\theta \), a veces es útil usar\(( - \pi , \pi ) \) en su lugar.

Ejemplo\(\PageIndex{2}\)

Si un punto\(P\) tiene coordenadas cartesianas (−1, 1), entonces sus coordenadas polares son\(\left(\sqrt{2}, \frac{3 \pi}{4}\right)\).

Ejemplo\(\PageIndex{3}\)

Un punto con coordenadas polares\(\left(3, \frac{\pi}{6}\right)\) tiene coordenadas cartesianas\(\left(\frac{3 \sqrt{3}}{2}, \frac{3}{2}\right)\).

En nuestro contexto actual, queremos pensar en el mapeo de coordenadas polares

\[(x, y)=F(r, \theta)=(r \cos (\theta), r \sin (\theta)) \]

como un cambio de variables entre el plano\(r \theta \) - y el\(xy\) plano. Este mapeo es particularmente útil para nosotros porque mapea regiones rectangulares en el\(r \theta \) plano -sobre regiones circulares en el\(xy\) plano -plano. Por ejemplo, para cualquiera\(a>0\),\(F\) mapea la región rectangular

\[ E=\{(r, \theta): 0 \leq r \leq a, 0 \leq \theta<2 \pi\} \nonumber \]

en el\(r \theta \) plano -sobre el disco cerrado

\[ D=\bar{B}^{2}((0,0), a)=\left\{(x, y): x^{2}+y^{2} \leq a\right\} \nonumber \]

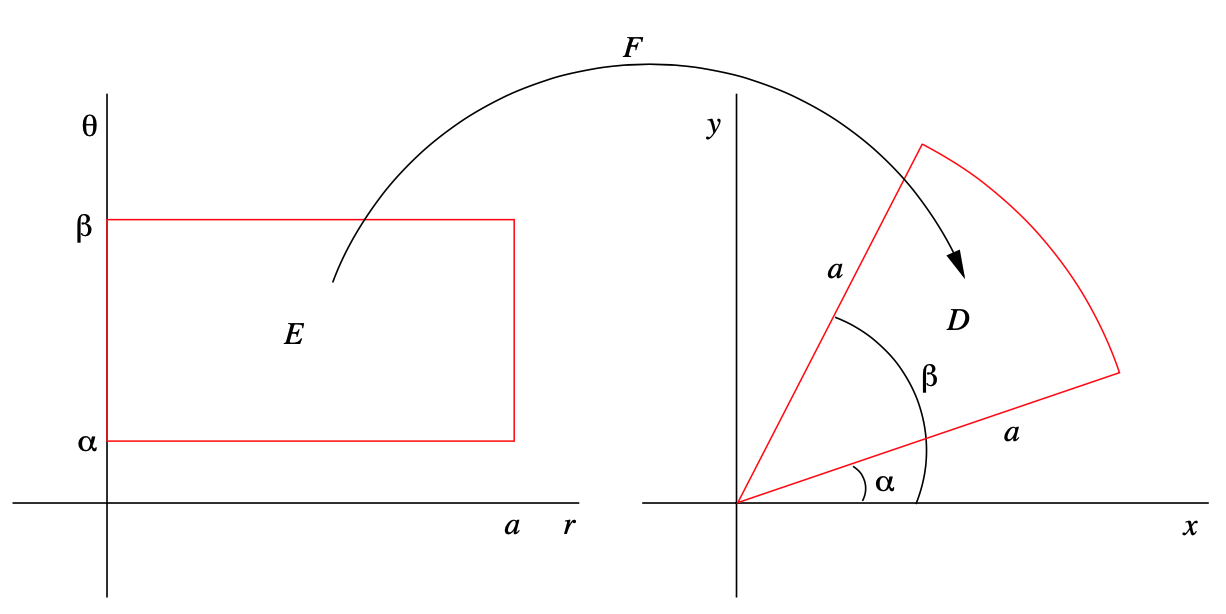
en el\(xy\) plano -( ver Figura 3.7.5 a continuación para un ejemplo). De manera más general, para cualquier\( 0 \leq \alpha < \beta < 2 \pi \),\(F\) mapea la región rectangular

\[ E=\{(r, \theta): 0 \leq r \leq a, \alpha \leq \theta<\beta\} \nonumber \]

en el\(r \theta \) plano sobre una región\(D\) en el\(xy\) plano que es el sector del disco cerrado\(\bar{B}^{2}((0,0), a)\) que se encuentra entre radios de ángulos\(\alpha \) y\(\beta \) (ver Figura 3.7.4).

Figura\(\PageIndex{4}\): Cambio de coordenadas polares de variables

Figura\(\PageIndex{5}\): Cambio de coordenadas polares de mapas de variables\([0,2] \times[0,2 \pi]\) a\(\bar{B}^{2}((0,0), 2)\)

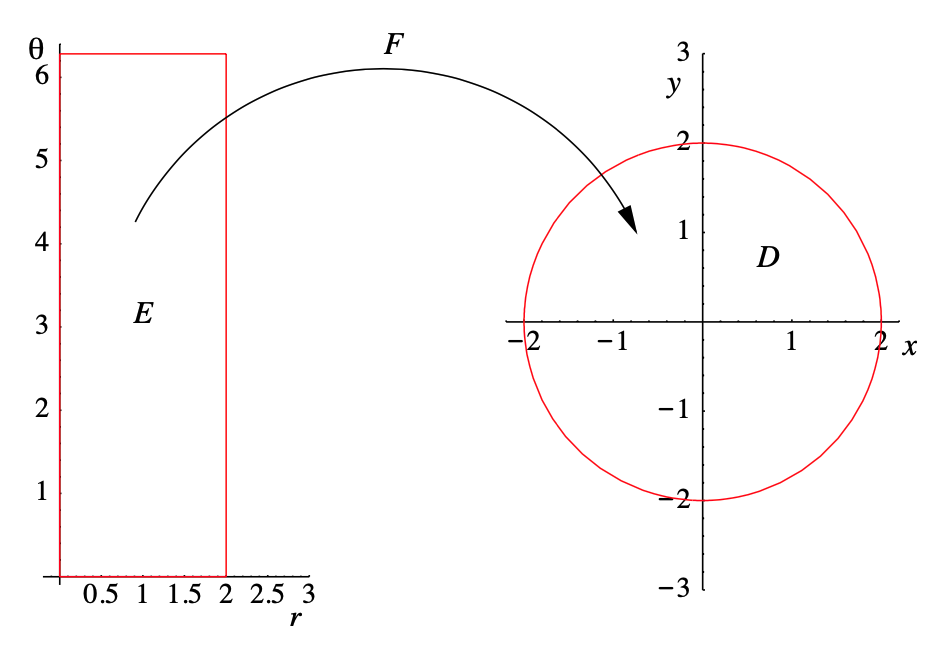
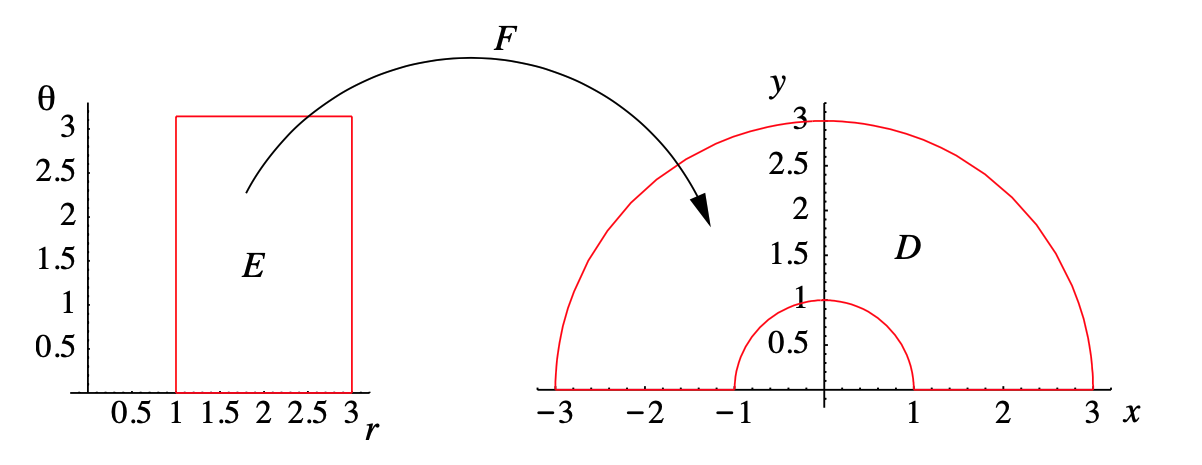
Otro ejemplo básico es un anillo: para cualquiera\(0 < a < b\),\(F\) mapea la región rectangular

\[ E=\{(r, \theta): a \leq r \leq b, 0 \leq \theta<2 \pi\} \nonumber \]

en el\(r \theta \) plano -sobre el anillo

\[ D=\left\{(x, y): a \leq x^{2}+y^{2} \leq b\right\} \nonumber \]

en el\(xy\) -avión. La Figura 3.7.6 ilustra este mapeo para la mitad superior de un anillo.

Figura\(\PageIndex{6}\): Mapa de coordenadas polares\([1,3] \times[0, \pi]\) a la mitad superior de un anillo

Ejemplo\(\PageIndex{4}\)

\(V\)Sea el volumen de la región que se encuentra debajo del paraboloide con ecuación\(z=4-x^{2}-y^{2}\) y por encima del\(xy\) plano. En la Sección 3.6, vimos que

\[ V=\iint_{D}\left(4-x^{2}-y^{2}\right) d x d y=8 \pi , \nonumber \]

donde

\[ D=\left\{(x, y): x^{2}+y^{2} \leq 4\right\} . \nonumber \]

El uso de coordenadas polares simplifica enormemente la evaluación de esta integral. Con el cambio de coordenadas polares de variables

\[ x=r \cos (\theta) \nonumber \]

y

\[ y=r \sin (\theta) , \nonumber \]

el disco cerrado\(D\) en el\(xy\) plano corresponde al rectángulo cerrado

\[ E=\{(r, \theta): 0 \leq r \leq 2,0 \leq \theta \leq 2 \pi\} \nonumber \]

en el\(r \theta \) plano -( ver Figura 3.7.5 anterior). Tenga en cuenta que al describir\(E\) hemos permitido\(\theta = 2 \pi \), pero esto no afecta a nuestro resultado ya que una línea no tiene área en\(\mathbb{R}^2\). Además, si dejamos\(f(x, y)=4-x^{2}-y^{2}\), entonces

\ [\ begin {alineado}
f (F (r,\ theta)) &=f (r\ cos (\ theta), r\ sin (\ theta))\\
&=4-r^ {2}\ cos ^ {2} (\ theta) -r^ {2}\ sin (\ theta)\\
&=4-r^ {2}\ izquierda (\ cos ^ {2} (\ theta) +\ sin ^ {2} (\ theta)\ derecha. \\
&=4-r^ {2},
\ end {alineado}\]

lo que también se desprende del hecho de que\(r^{2}=x^{2}+y^{2}\). Ahora

\ [\ frac {\ parcial (x, y)} {\ parcial (r,\ theta)} =\ izquierda [\ begin {array} {ll}\ frac {
\ parcial} {\ parcial} {\ parcial} r\ cos (\ theta) &\ frac {\ parcial} {\ parcial\ theta} r\ cos (\ theta)\\ frac {\ parcial} {
\ parcial} r\ cos (\ theta)\ frac {\ parcial} r\ sin (\ theta) &\ frac {\ parcial} {\ parcial\ theta} r\ sin (\ theta)
\ end {array}\ right] =\ left [\ begin {array} {cr}
\ cos (\ theta) & -r\ sin (\ theta)\\\ sin (
\ theta)\\ sin (\ theta) & r\ cos (\ theta)
\ end {array}\ derecha],\]

por lo

\[ \operatorname{det} \frac{\partial(x, y)}{\partial(r, \theta)}=r \cos ^{2}(\theta)+r \sin ^{2}(\theta)=r\left(\cos ^{2}(\theta)+\sin ^{2}(\theta)\right)=r . \]

Por lo tanto, usando (\(\ref{3.7.5}\)), tenemos

\ [\ begin {alineado}
\ iint_ {D}\ izquierda (4-x^ {2} -y^ {2}\ derecha) d x d y &=\ iint_ {E}\ izquierda (4-r^ {2}\ derecha)\ izquierda|\ nombreoperador {det}\ frac {\ parcial (x, y)} {\ parcial (r,\ theta)}\ derecha| d r d\ theta\\
&=\ int_ {0} ^ {2}\ int_ {0} ^ {2\ pi}\ izquierda (4-r^ {2}\ derecha) r d\ theta d r\\
&= \ int_ {0} ^ {2} 2\ pi\ izquierda (4 r-r^ {3}\ derecha) d r\\
&=\ izquierda.2\ pi\ izquierda (2 r^ {2} -\ frac {r^ {4}} {4}\ derecha)\ derecha|_ {0} ^ {2}\\
&=2\ pi (8-4)\\
&=8\ pi.
\ end {alineado}\]

Ejemplo\(\PageIndex{5}\)

Supongamos que\(D\) es la parte de la región entre los círculos con ecuaciones\(x^2 + y^2 = 1\) y\(x^2 + y^2 = 9\) que se encuentra por encima del\(x\) eje -eje. Es decir,

\[ D=\left\{(x, y): 1 \leq x^{2}+y^{2} \leq 9, x \geq 0\right\} . \nonumber \]

Deseamos evaluar

\[ \iint_{D} e^{-\left(x^{2}+y^{2}\right)} d x d y . \nonumber \]

Bajo el cambio de coordenadas polares de variables

\[ x=r \cos (\theta) \nonumber \]

y

\[ y=r \sin (\theta) , \nonumber \]

la región anular\(D\) corresponde al rectángulo cerrado

\[ E=\{(r, \theta): 1 \leq r \leq 3,0 \leq \theta \leq \pi\} , \nonumber \]

como se ilustra en la Figura 3.7.6 anterior. Además,\(x^2 + y^2 = r^2\) y, como vimos en el ejemplo anterior,

\[ \left|\operatorname{det} \frac{\partial(x, y)}{\partial(r, \theta)}\right|=r . \nonumber \]

De ahí

\ [\ begin {alineado}
\ iint_ {D} e^ {-\ izquierda (x^ {2} +y^ {2}\ derecha)} d x d y &=\ iint_ {E} r e^ {-r^ {2}} d r d\ theta\
&=\ int_ {1} ^ {3}\ int_ {0} ^ {\ pi} r e^ {-r^ {2}} d\ theta d r\\
&=\ int_ {1} ^ {3}\ pi r e^ {-r^ {2}} d r\\
&=-\ izquierda. \ frac {\ pi} {2} e^ {-r^ {2}}\ derecha|_ {1} ^ {3}\
&=\ frac {\ pi} {2}\ izquierda (e^ {-1} -e^ {-9}\ derecha).
\ end {alineado}\]

Obsérvese que en este caso el cambio de variables no sólo simplificó la región de integración, sino que también puso la función que se integraba en una forma a la que podríamos aplicar el Teorema Fundamental del Cálculo.

Coordenadas esféricas

A continuación considere la siguiente extensión de coordenadas polares a tres espacios: dado un punto\(P\) con coordenadas cartesianas\((x,y,z)\), dejar\(\rho\) ser la distancia desde\(P\) el origen,\( \theta \) ser la coordenada angular para el polar coordenadas de\((x,y,0)\) (la proyección de\(P\) sobre el\(xy\) -plano), y dejar\(\varphi \) ser el ángulo entre el vector desde el origen hasta\(P\) y el\(z\) eje positivo, medido de 0 a\(\pi \). Si\(x \neq 0 \), tenemos

\[ \rho=\sqrt{x^{2}+y^{2}+z^{2}} , \]

\[ \tan (\theta)=\frac{y}{x} , \]

y

\[ \cos (\varphi)=\frac{z}{\sqrt{x^{2}+y^{2}+z^{2}}} , \]

dónde\(0 \leq \theta<2 \pi\) y\(0 \leq \varphi \leq \pi\). Al igual que con las coordenadas polares\(y>0\),\(\theta = \frac{\pi}{2}\) si\(x=0\) dejamos\(\theta = \frac{3 \pi}{2}\) si\(y<0\), y\(\theta\) es indefinido si\(y=0\). Ver Figura 3.7.7.

Figura\(\PageIndex{7}\): Coordenadas esféricas y cartesianas para un punto\(P\)

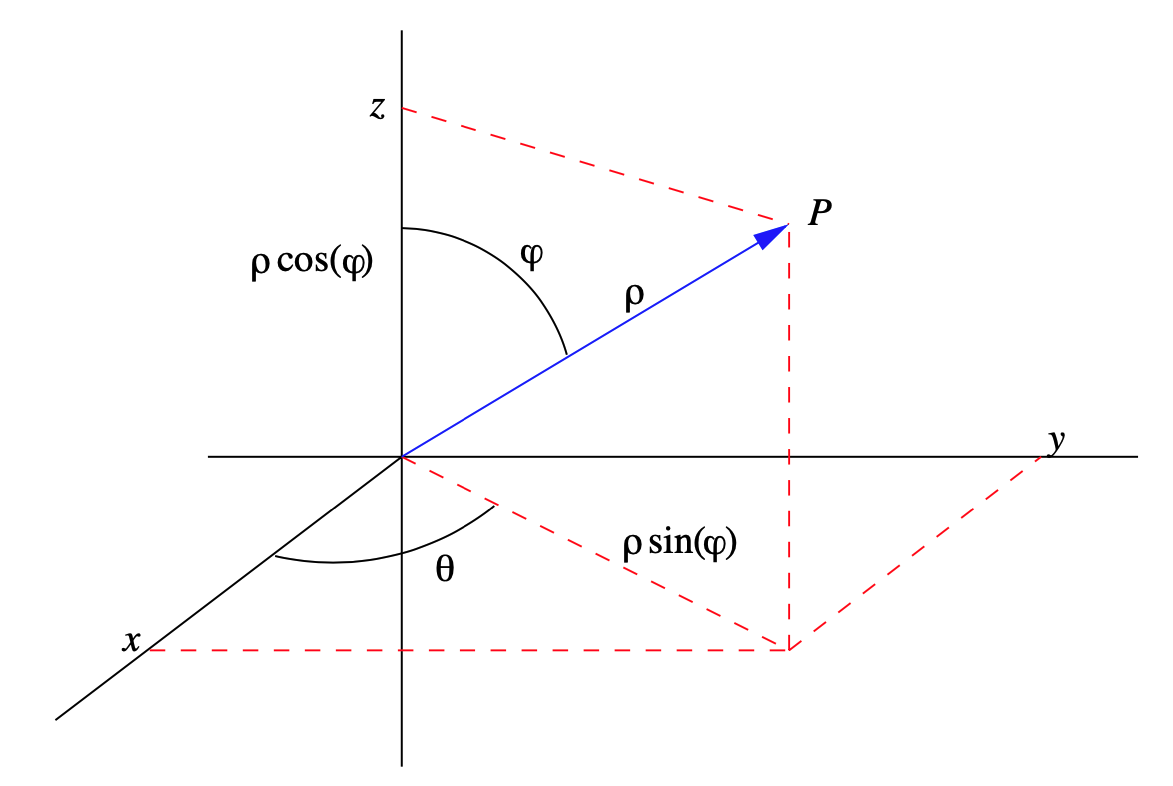
Por el contrario, dado un punto\(P\) con coordenadas esféricas\(( \rho , \theta , \varphi )\), la proyección de\(P\) sobre el\(xy\) plano tendrá coordenada polar\(r=\rho \sin (\varphi)\). De ahí que las coordenadas cartesianas de\(P\) son

\[ x=\rho \cos (\theta) \sin (\varphi) , \]

\[ y=\rho \sin (\theta) \sin (\varphi) , \]

y

\[ z=\rho \cos (\varphi) . \]

Ejemplo\(\PageIndex{6}\)

Si un punto\(P\) tiene coordenadas cartesianas (2, −2, 1), entonces sus coordenadas esféricas satisfacen

\[ \rho=\sqrt{4+4+1}=3 , \nonumber \]

\[ \tan (\theta)=\frac{-2}{2}=-1 , \nonumber \]

y

\[ \cos (\varphi)=\frac{1}{\sqrt{4+4+1}}=\frac{1}{3} . \nonumber \]

De ahí que tengamos

\[ \theta=\frac{7 \pi}{4} \nonumber \]

y

\[ \varphi=\cos ^{-1}\left(\frac{1}{3}\right)=1.2310 , \nonumber \]

donde hemos redondeado el valor de\(\varphi \) a cuatro decimales. De ahí\(P\) que tenga coordenadas esféricas\(\left(3, \frac{7 \pi}{4}, 1.2310\right)\).

Ejemplo\(\PageIndex{7}\)

Si un punto\(P\) tiene coordenadas esféricas\(\left(4, \frac{\pi}{3}, \frac{3 \pi}{4}\right)\), entonces sus coordenadas cartesianas son

\[ x=4 \cos \left(\frac{\pi}{3}\right) \sin \left(\frac{3 \pi}{4}\right)=4\left(\frac{1}{2}\right)\left(\frac{1}{\sqrt{2}}\right)=\sqrt{2} , \nonumber \]

\[ y=4 \sin \left(\frac{\pi}{3}\right) \sin \left(\frac{3 \pi}{4}\right)=4\left(\frac{\sqrt{3}}{2}\right)\left(\frac{1}{\sqrt{2}}\right)=\sqrt{6} , \nonumber \]

y

\[ z=4 \cos \left(\frac{3 \pi}{4}\right)=4\left(-\frac{1}{\sqrt{2}}\right)=-2 \sqrt{2} . \nonumber \]

Análogamente a nuestro trabajo con coordenadas polares, pensamos en el mapeo de coordenadas esféricas

\[ (x, y, z)=F(\rho, \theta, \varphi)=(\rho \cos (\theta) \sin (\varphi), \rho \sin (\theta) \sin (\varphi), \rho \cos (\varphi)) \label{3.7.19} \]

como un cambio de variables entre\(\rho \theta \varphi \) -espacio y\(xyz\) -espacio. Este mapeo es particularmente útil para evaluar integrales triples porque mapea regiones rectangulares en el\(\rho \theta \varphi \) espacio sobre regiones\(xyz\) esféricas en el espacio. Para el ejemplo más básico, para cualquier\(a>0\),\(F\) mapea la región rectangular

\[ E=\{(\rho, \theta, \varphi): 0 \leq \rho \leq a, 0 \leq \theta<2 \pi, 0 \leq \varphi \leq \pi\} \nonumber \]

en\(\rho \theta \varphi \) el espacio sobre la bola cerrada

\[ D=\bar{B}^{3}((0,0,0), a)=\left\{(x, y, z): x^{2}+y^{2}+z^{2} \leq a\right\} \nonumber \]

en el\(xyz\) espacio. De manera más general, para cualquier\(0<a<b, 0 \leq \alpha<\beta<2 \pi\), y\(0 \leq \gamma<\delta \leq \pi, F\) mapea la región rectangular

\[ E=\{(\rho, \theta, \varphi): a \leq \rho \leq b, \alpha \leq \theta<\beta, \gamma \leq \varphi \leq \delta\} \nonumber \]

sobre una región\(D\) en el\(xyz\) espacio que se encuentra entre las esferas concéntricas\(S^{2}((0,0,0), a)\) y\(S^{2}((0,0,0), b)\), y para la cual el ángulo\(\theta \) se encuentra entre\(\alpha\) y\(\beta\) y el ángulo\(\varphi\) entre \(\gamma\)y\(\delta\). Por ejemplo, si\(\alpha=0, \beta=\pi, \gamma=0\), y\(\delta = \frac{\pi}{2}\), entonces\(D\) es la mitad de la región que se encuentra entre dos hemisferios concéntricos con radios\(a\) y\(b\).

Antes de usar el cambio de coordenadas esféricas de la variable in (\(\ref{3.7.19}\)) para evaluar una integral usando (\(\ref{3.7.5}\)), necesitamos computar el determinado del jacobiano de\(F\). Ahora

\ [\ begin {align}
\ frac {\ parcial (x, y, z)} {\ parcial (\ rho,\ theta,\ varphi)} =&\ left [\ begin {array} {ccc}
\ frac {\ parcial} {\ parcial} {\ rho}\ rho\ cos (\ theta)\ sin (\ varphi) &\ frac {\ parcial} {\ parcial\ theta}\ rho\ cos (\ theta)\ sin (\ varphi) &\ frac {\ parcial} {\ parcial\ varphi}\ rho\ cos (\ theta)\ sin (\ varphi)\ nonumber\
\ frac {\ parcial} {\ parcial\ rho}\ rho\ sin (\ theta)\ sin (\ varphi) &\ frac {\ parcial} {\ parcial\ theta}\ rho\ sin (\ theta)\ sin (\ varphi) &\ frac {\ parcial}\ parcial\ varphi}\ rho\ sin (\ theta)\ sin (\ varphi)\ nonumber\\
\ frac {\ parcial} {\ parcial\ rho}\ rho\ cos (\ varphi) &\ frac {\ parcial} {\ parcial\ theta}\ rho\ cos (\ varphi) &\ frac {\ parcial} {\ parcial\ varphi}\ rho\ cos (\ varphi)
\ end {array}\ derecha]\ nonumber\\
&=\ izquierda [\ begin {array} ccc}
\ cos (\ theta)\ sin (\ varphi) & -\ rho\ sin (\ theta)\ sin (\ varphi) &\ rho\ cos (\ theta)\ cos (\ varphi)\ nonumber\
\ sin (\ theta)\ sin (\ varphi) &\ rho\ cos (\ theta)\ sin (\ varphi) &\ rho\ sin (\ theta)\ cos (\ varphi)\ nonumber\
\ cos (\ varphi) & 0 & -\ rho\ sin (\ varphi)\ nonumber
\ fin {array}\ derecha]\ label {}
\ end {align}\]

entonces, expandiéndose a lo largo de la tercera fila,

\ [\ begin {align}
\ nombreoperador {det}\ frac {\ parcial (x, y, z)} {\ parcial (\ rho,\ theta,\ varphi)} =&\ cos (\ varphi)\ izquierda (-\ rho^ {2}\ sin ^ {2} (\ theta)\ sin (\ varphi)\ cos (\ varphi) -\ rho^ {2}\ cos ^ {2} (\ theta)\ sin (\ varphi)\ cos (\ varphi)\ derecha)\ nonumber\\
&-\ rho\ sin (\ varphi)\ izquierda (\ rho\ cos ^ {2} (\ theta)\ sin ^ {2} (\ varphi) +\ rho\ sin ^ {2} (\ theta)\ sin ^ {2} (\ varphi)\ derecha. \ nonumber\\
=&-\ rho^ {2}\ sin (\ varphi)\ cos ^ {2} (\ varphi)\ izquierda (\ sin ^ {2} (\ theta) +\ cos ^ {2} (\ theta)\ derecha) -\ rho^ {2}\ sin ^ {3} (\ varphi)\ izquierda (\ sin ^ {2} (\ theta) +\ cos ^ {2} (\ theta)\ derecha)\ nonumber\\
=&-\ rho^ {2}\ sin (\ varphi)\ cos ^ {2} (\ varphi) -\ rho^ {2}\ sin ^ {3} (\ varphi)\ nonumber\\
=&-\ rho^ {2}\ sin (\ varphi)\ izquierda (\ cos ^ {2} (\ varphi) +\ sin ^ {2} (\ varphi)\ derecha)\ nonumber\\
=&-\ rho^ {2}\ sin (\ varphi)\ label {}
\ end {align}\]

Ahora\(\rho \geq 0\) y, desde\(0 \leq \varphi \leq \pi, \sin (\varphi) \geq 0\), entonces

\[ \left|\frac{\partial(x, y, z)}{\partial(\rho, \theta, \varphi)}\right|=\rho^{2} \sin (\varphi) . \label{3.7.22} \]

Ejemplo\(\PageIndex{8}\)

En un ejemplo anterior se utilizó el hecho de que el volumen de una esfera de radio 1 es\(\frac{4 \pi}{3}\). En este ejemplo verificaremos que el volumen de una esfera de radio\(a\) es\(\frac{4}{3} \pi a^{3}\). Que\(V\) sea el volumen de

\[ D=\bar{B}^{3}((0,0,0), a) , \nonumber \]

la bola cerrada de radio\(a\) centrada en el origen en\(\mathbb{R}^3\). Entonces

\[ V=\iiint_{D} d x d y d z . \nonumber \]

Aunque podemos evaluar esta integral usando coordenadas cartesianas, nos resultará significativamente más fácil usar coordenadas esféricas. Uso del cambio de coordenadas esféricas de variables

\ [\ begin {alineado}
&x=\ rho\ cos (\ theta)\ sin (\ varphi),\\
&y=\ rho\ sin (\ theta)\ sin (\ varphi),
\ end {alineado}\]

y

\[ z=\rho \cos (\varphi) , \nonumber \]

la región\(D\) en\(xyz\) -espacio corresponde a la región

\[ E=\{(\rho, \theta, \varphi): 0 \leq \rho \leq a, 0 \leq \theta \leq 2 \pi, 0 \leq \varphi \leq \pi\} \nonumber \]

en el\(\rho \theta \varphi \) espacio. Usando (\(\ref{3.7.22}\)) en el cambio de variables formula (\(\ref{3.7.5}\)), tenemos

\ [\ comenzar {alineado}
V &=\ iiint_ {D} d x d y d z\\
&=\ iiint_ {E}\ izquierda|\ nombreoperador {det}\ frac {\ parcial (x, y, z)} {\ parcial (\ rho,\ theta,\ varphi)}\ derecha| d\ rho d\ theta d\ varphi\
=\ int_ {0} ^ {1}\ int_ {0} ^ {2\ pi}\ int_ {0} ^ {\ pi}\ rho^ {2}\ sin (\ varphi) d\ varphi d\ theta d\ rho\\
&=\ izquierda. \ int_ {0} ^ {a}\ int_ {0} ^ {2\ pi}\ izquierda (-\ rho^ {2}\ cos (\ varphi)\ derecha)\ derecha|_ {0} ^ {\ pi} d\ theta d\ rho\\
&=\ int_ {0} ^ {a}\ int_ {0} ^ {2\ pi}\ izquierda (-\ ^ {2} (-1-1)\ derecha) d\ theta d\ rho\\
&=2\ int_ {0} ^ {a}\ int_ {0} ^ {2\ pi}\ rho^ {2} d\ theta d\ rho\\
&=4\ pi\ int _ {0} ^ {a}\ rho^ {2} d\ rho\\
&=\ izquierda. \ frac {4\ pi} {3}\ rho^ {3}\ derecha|_ {0} ^ {a}\\
&=\ frac {4} {3}\ pi a^ {3}.
\ end {alineado}\]

Ejemplo\(\PageIndex{9}\)

Supongamos que deseamos evaluar

\[ \iiint_{D} \log \sqrt{x^{2}+y^{2}+z^{2}} d x d y d z , \nonumber \]

donde\(D\) está la región en la\(\mathbb{R}^3\) que se encuentra entre las dos esferas con ecuaciones\(x^{2}+y^{2}+z^{2}=1\)\(x^{2}+y^{2}+z^{2}=4\) y y por encima del\(xy\) plano. Bajo el cambio de coordenadas esféricas de variables

\[ x=\rho \cos (\theta) \sin (\varphi) , \nonumber \]

\[ y=\rho \sin (\theta) \sin (\varphi) , \nonumber \]

y

\[ z=\rho \cos (\varphi) , \nonumber \]

la región\(D\) en\(xyz\) -espacio corresponde a la región

\[ E=\left\{(\rho, \theta, \varphi): 1 \leq \rho \leq 2,0 \leq \theta \leq 2 \pi, 0 \leq \varphi \leq \frac{\pi}{2}\right\} \nonumber \]

en el\(\rho \theta \varphi \) espacio. Usando (\(\ref{3.7.22}\)) en el cambio de variables formula (\(\ref{3.7.5}\)), tenemos

\ [\ begin {alineado}
\ iiint_ {D}\ log\ sqrt {x^ {2} +y^ {2} +z^ {2}} d x d y d z &=\ iiint_ {E}\ log (\ rho)\ izquierda|\ frac {\ parcial (x, y, z)} {\ parcial (\ rho,\ theta,\ varphi)}\ derecha| d\ rho d\ theta d\ varphi\\
&=\ int_ {1} ^ {2}\ int_ {0} ^ {2\ pi}\ int_ {0} ^ {\ frac {\ pi} {2}}\ rho^ {2}\ log (\ rho)\ sin (\ varphi) d\ varphi d\ theta d\ rho\\
&=\ izquierda. \ int_ {1} ^ {2}\ int_ {0} ^ {2\ pi}\ izquierda (-\ rho^ {2}\ log (\ rho)\ cos (\ varphi)\ derecha)\ derecha|_ {0} ^ {\ frac {\ pi} {2}} d\ theta d\ rho\
&=\ int_ {1} ^ {2}\ int_ {0} ^ {2\ pi}\ izquierda (-\ rho^ {2}\ log (\ rho)\ derecha) (0-1) d\ theta d\ rho\\
&=\ int_ {1} ^ {2}\ int_ {0} ^ {2\ pi}\ rho^ {2}\ log (\ rho) d\ theta d\ rho\\
&=2\ pi\ int_ {1} ^ {2}\ rho^ {2}\ log (\ rho) d\ rho.
\ end {alineado}\]

Utilizamos la integración por partes para evaluar esta integral final: dejar

\[ u = log(\rho) \\ dv = \rho^2 d \rho \\ \\ du = \frac{1}{\rho} d \rho \\ v = \frac{\rho^3 }{3}, \nonumber \]

tenemos

\ [\ begin {alineado}
\ iiint_ {D}\ log\ sqrt {x^ {2} +y^ {2} +z^ {2}} d x d y d z &=2\ pi\ left (\ left. \ frac {1} {3}\ rho^ {3}\ log (\ rho)\ derecha|_ {1} ^ {2} -\ frac {1} {3}\ int_ {1} ^ {2}\ rho^ {2} d\ rho\ derecha)\\
&=\ frac {16} {3}\ pi\ log (2) -\ izquierda. \ frac {2\ pi\ rho^ {3}} {9}\ derecha|_ {1} ^ {2}\\
&=\ frac {16} {3}\ pi\ log (2) -\ frac {14\ pi} {9}\\
&=\ frac {2\ pi} {3}\ left (8\ log (2) -\ frac {7} {3}\ derecha).
\ end {alineado}\]