4.4.E: Teorema de Green (Ejercicios)
- Page ID
- 111697
Ejercicio\(\PageIndex{1}\)
Dejado\(D\) ser el rectángulo cerrado adentro\(\mathbb{R}^2\) con vértices en (0, 0), (2, 0), (2, 4), y (0, 4), con límite\(\partial D\) orientado en sentido antihorario. Utilice el teorema de Green para evaluar las siguientes integrales de línea.
a)\(\int_{\partial D} 2 x y d x+3 x^{2} d y\)
b)\(\int_{\partial D} y d x+x d y\)
- Responder
-
a)\(\int_{\partial D} 2 x y d x+3 x^{2} d y=80\)
Ejercicio\(\PageIndex{2}\)
Dejado\(D\) ser el triángulo adentro\(\mathbb{R}^2\) con vértices en (0, 0), (2, 0), y (0, 4), con límite\(\partial D\) orientado en sentido antihorario. Utilice el teorema de Green para evaluar las siguientes integrales de línea.
a)\(\int_{\partial D} 2 x y^{2} d x+4 x d y\)
b)\(\int_{\partial D} y d x+x d y\)
c)\(\int_{\partial D} y d x-x d y\)
- Responder
-
a)\(\int_{\partial D} 2 x y^{2} d x+4 x d y=\frac{16}{3} \text { (c) } \int_{\partial D} y d x-x d y=-8\)
Ejercicio\(\PageIndex{3}\)
Usa el teorema de Green para encontrar el área de un círculo de radio\(r\).
Ejercicio\(\PageIndex{4}\)
Usa el teorema de Green para encontrar el área de la región\(D\) encerrada por el hipocicloide
\[ x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}} , \nonumber \]
donde\(a > 0\). Tenga en cuenta que podemos parametrizar esta curva usando
\[ \varphi(t)=\left(a \cos ^{3}(t), a \sin ^{3}(t)\right) , \nonumber \]
\(0 \leq t \leq 2 \pi\).
- Responder
-
\(\frac{3}{8} \pi a^{2}\)
Ejercicio\(\PageIndex{5}\)
Usa el teorema de Green para encontrar el área de la región encerrada por un “pétalo” de la curva parametrizada por
\[ \varphi(t)=(\sin (2 t) \cos (t), \sin (2 t) \sin (t)) . \nonumber \]
- Responder
-
\(\frac{\pi}{8}\)
Ejercicio\(\PageIndex{6}\)
Encuentra el área de la región encerrada por el cardioide parametrizado por
\[ \varphi(t)=((2+\cos (t)) \cos (t),(2+\cos (t)) \sin (t)) , \nonumber \]
\(0 \leq t \leq 2 \pi\).
- Responder
-
\(\frac{9 \pi}{2}\)
Ejercicio\(\PageIndex{7}\)
Verificar (4.4.23), completando así la prueba del teorema de Green.
Ejercicio\(\PageIndex{8}\)
Supongamos que el campo vectorial\(F: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}\) con funciones de coordenadas\(p=F_{1}(x, y)\) y\(q=F_{2}(x, y)\) está\(C^1\) en un conjunto abierto que contiene la región Tipo III\(D\). Además, supongamos que\(F\) es el gradiente de una función escalar\(f: \mathbb{R}^{2} \rightarrow \mathbb{R}\).
a) Demostrar que
\[ \frac{\partial q}{\partial x}-\frac{\partial p}{\partial y}=0 \nonumber \]
para todos los puntos\((x,y)\) en\(D\).
b) Utilizar el teorema de Green para demostrar que
\[ \int_{\partial D} p d x+q d y=0 , \nonumber \]
donde\(\partial D\) es el límite de\(D\) con orientación en sentido antihorario.
Ejercicio\(\PageIndex{9}\)
¿Cuántas formas conoces para calcular el área de un círculo?
Ejercicio\(\PageIndex{10}\)
¿Quién era George Green?
Ejercicio\(\PageIndex{11}\)
Explicar cómo el teorema de Green es una generalización del Teorema Fundamental del Cálculo Integral.
Ejercicio\(\PageIndex{12}\)
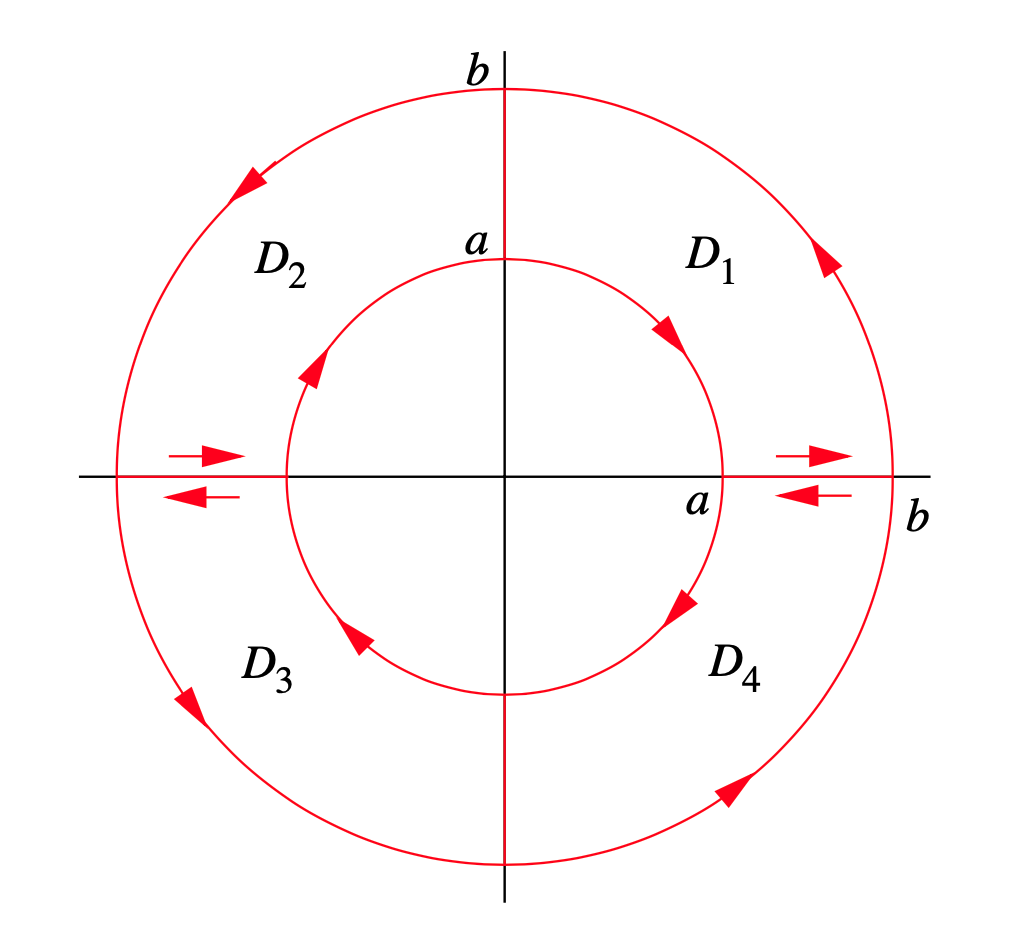
Dejar\(b > a\), dejar\(C_1\) ser el círculo de radio\(b\) centrado en el origen, y dejar\(C_2\) ser el círculo de radio\(a\) centrado en el origen. Si\(D\) es la región anular entre\(C_1\) y\(C_2\) y\(F\) es un campo\(C^1\) vectorial con funciones de coordenadas\(p=F_{1}(x, y)\) y\(q=F_{2}(x, y)\), mostrar que
\[ \iint_{D}\left(\frac{\partial q}{\partial x}-\frac{\partial p}{\partial y}\right) d x d y=\int_{C_{1}} p d x+q d y+\int_{C_{2}} p d x+q d y , \nonumber \]
donde\(C_1\) está orientado en sentido contrario a las agujas del reloj y\(C_2\) está orientado en el sentido de las agujas del reloj. (Pista: Descomponerse\(D\) en regiones Tipo III\(D_1\),\(D_2\), y\(D_3\)\(D_4\), cada una con límite orientado en sentido antihorario, como se muestra en la Figura 4.4.5.)